半挂式车辆自主驾驶的轨迹跟踪控制研究
张 勇,王同祥
(1.黄河交通学院,河南 焦作 454950; 2.郑州宇通客车股份有限公司,河南 郑州 450000)
0 引 言
半挂式车辆由于具备运货效率高、能够有效降低成本以及减少不必要的加工包装环节等优势,在农业机械、交通运输等领域的需求不断增长[1]。然而,半挂式车辆的驾驶难度较大,容易导致驾驶员疲劳,成为影响其应用推广的瓶颈。
近年来,随着计算机技术以及车辆控制技术的日益进步,自主驾驶车辆技术迅速发展,并在商用车领域取得了长足进步[2-3]。由于具备自主感知和理解环境、规划和控制自身运动、完成预定任务的能力,相对于有人驾驶车辆,自主驾驶车辆可以降低或免除驾驶员的劳动强度,消除引起交通事故的潜在因素,成为汽车产业发展的一个重要趋势[4]。因此研究半挂式车辆的自主驾驶对减轻驾驶员的工作量、改善交通安全具有重要意义。
针对半挂式车辆的轨迹跟踪控制是实现其自主驾驶所面临的重要挑战之一。首先,相比于一般车辆,半挂式车辆的运动控制不仅需要考虑车辆的非完整性约束,还需要考虑到牵引车与拖车所构成的欠驱动、非完整系统。其次,现有的惯性测量仪器成本较高,难以在商用车上大规模装备,这导致半挂式车辆的航向难以直接测量,增加了其轨迹跟踪的难度。最后,半挂式车辆的轨迹跟踪控制还需要适应不同的道路曲率。因此,研究半挂式车辆的轨迹跟踪控制有显著的理论价值。
目前,国内外的学者在自主驾驶车辆的轨迹跟踪控制领域做了大量的研究[4-9]。赵熙俊[5]和安林芳[6]等采用传统的PID控制方法进行车辆轨迹跟踪,表现出较好的跟踪能力,但是难以满足复杂工况下的应用;姜岩[7]等采用了预瞄方法进行车辆的轨迹跟踪研究,实车测试结果表明它对存在较大跟踪偏差以及不连续性的轨迹具有较强的鲁棒性,但是预瞄距离的自适应选取仍是一个难点。游峰[8]等采用BackStepping算法设计自主驾驶车辆换道行为的轨迹跟踪控制器。文献[9-11]基于二次型最优控制器解决车辆轨迹跟踪问题,仿真结果表明由于车辆模型的线性化忽略了道路曲率影响,降低了其在曲率变化较大工况下的应用。ZHANG[12]等在对车辆模型进行迭代线性化的基础上发展出迭代LQR方法,能够降低车辆模型失配造成的问题。但是,上述方法不能有效适应半挂式车辆的运动特性。
本文通过研究半挂式车辆转向运动的特点,建立了运动学模型,并将其线性化得到轨迹跟踪的线性误差模型。针对半挂式车辆的航向难以测量的问题,基于扩展卡尔曼滤波(EKF)设计了车辆状态估计器。在对期望轨迹进行自适应拟合的基础上,利用迭代LQR方法,通过使得在预测时域内的轨迹跟踪误差最小化得到最优的反馈控制序列,得到了针对半挂式车辆的轨迹跟踪控制器,并在Simulink环境中进行了仿真研究。
1 半挂式车辆建模
1.1 半挂式车辆的运动学模型
半挂式车辆的转向过程如图1所示。假设车辆在水平面内做平面运动,且车轮与地面之间无相对滑动,大地坐标系为OXY,X轴和Y轴分别指向正东方向和正北方向。
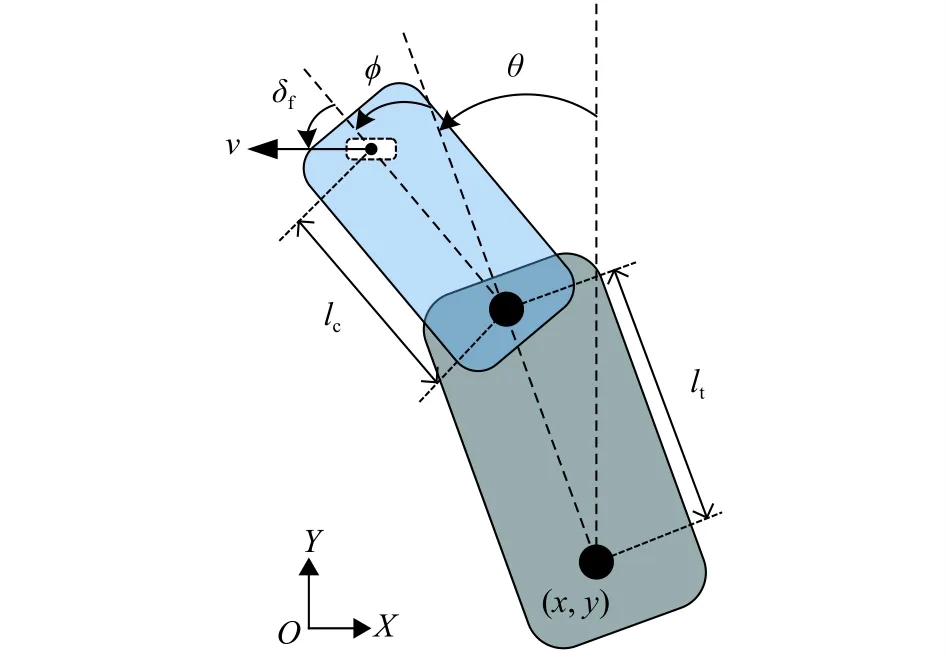
图 1 半挂式车辆转向过程示意图
满足车辆非完整约束的运动方程为
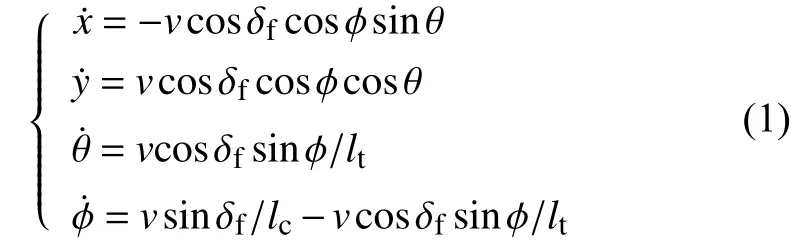
式中:(x,y)——半挂式车辆的后轴中心位置;
θ——半挂式车辆拖车与Y轴的夹角;
φ——牵引车与拖车车轴之间的夹角;
δf——牵引车的前轮转向角;
lc,lt——牵引车前轴到联结点的距离和拖车后轴到联结点的距离;
v——车辆前轮中心的速度。

其中,f为连续可微的方程。
1.2 半挂式车辆路径跟踪的线性误差模型
由于式(2)为非线性模型,这里相对于期望轨迹对其进行线性化。假设期望轨迹表示为

将期望轨迹上的期望轨迹点(χr,ur)泰勒展开,并忽略高阶部分,可得
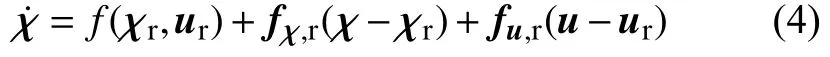
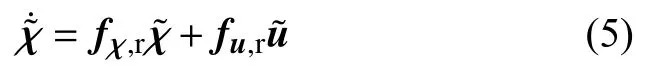
对式(5)进行离散化,可得到其离散线性时变模型:

2 基于EKF的状态估计
由于成本的限制,半挂式车辆的航向角难以直接测量,针对这一问题,设计基于EKF的状态观测器。考虑过程噪声,则式(2)可以表示为:

其中,w=[w1w2w3w4]T为过程噪声。
由于半挂式车辆后轴的中心坐标(x,y)可以通过GPS测量,牵引车与拖车车轴之间的夹角 φ可以通过编码器获得,可以得到车辆状态的测量方程
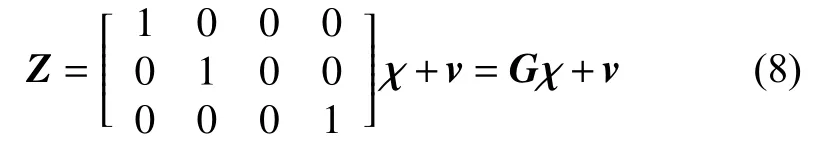
其中,Z=[z1z2z3]T为测量得到的后轴中心坐标以及牵引车与拖车车轴之间的夹角。v=[v1v2v3]T为测量噪声。假设wk和vk均为零均值的高斯白噪声,则有
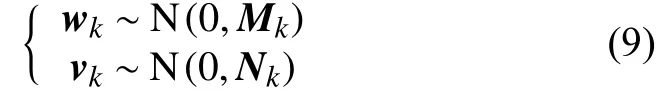
其中,Mk和Nk分别为wk和vk的协方差矩阵。
基于EKF的车辆状态估计器实现步骤如下:
1)初始化
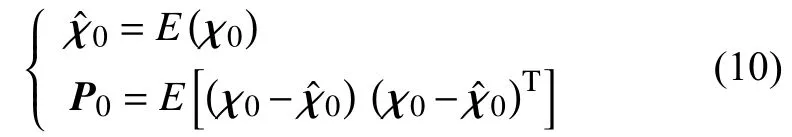
E——相应矢量或矩阵的期望。
2)状态更新
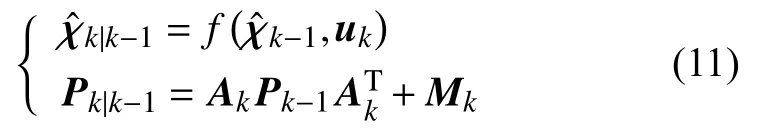
3)状态校正
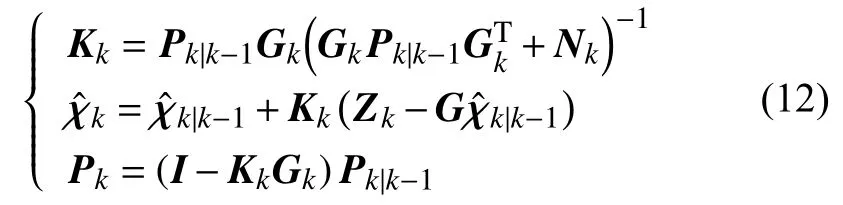
式中:Pk和Kk——协方差矩阵和估计增益;
I——单位矩阵。
3 半挂式车辆的轨迹跟踪控制
半挂式车辆自主驾驶轨迹跟踪可以描述为设计一个控制器,通过确定车辆控制输入u=[vδf]T,使得车辆到达并跟随给定的期望轨迹χr=[xryrθrφr]T。
在每一采样时刻k根据车辆当前位置和车速可以在期望轨迹上得到一系列的期望轨迹点,然后根据车辆的轨迹跟踪误差模型可以预测其在未来一段时域的状态[13]。通过设计性能评价指标并使其最小化,获得最优的控制量序列。最终半挂式车辆的轨迹跟踪控制器只采用最优控制序列中的第一个元素。半挂式车辆轨迹跟踪的示意图如图2所示。
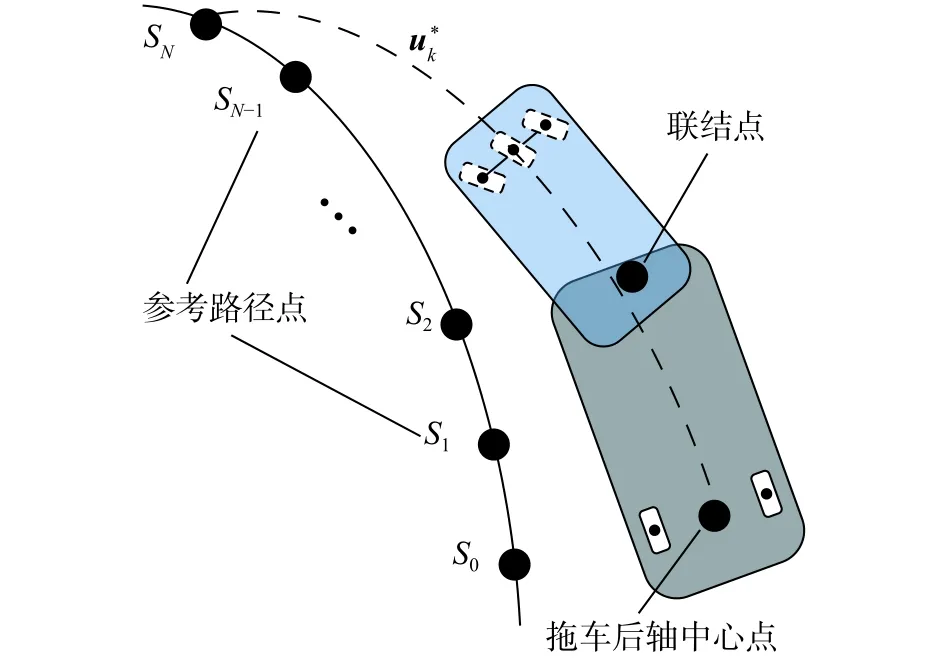
图 2 半挂式车辆路径跟踪示意图
3.1 基于三次Bezier曲线的自适应拟合
为了得到轨迹跟踪的前馈控制量,需要对离散的期望轨迹路点进行拟合。三次Bezier曲线由于具备良好的拟合能力和极强的描述能力,非常适用于期望轨迹的平滑与拟合,其表达式为:
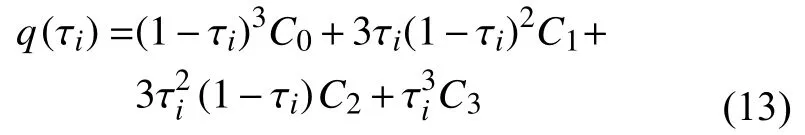
式中:q(τi)——参数 τi处的插值点,τi∈ [0,1];
C0和C3——期望轨迹上的控制点;
C1和C2——曲线拟合的中间点。
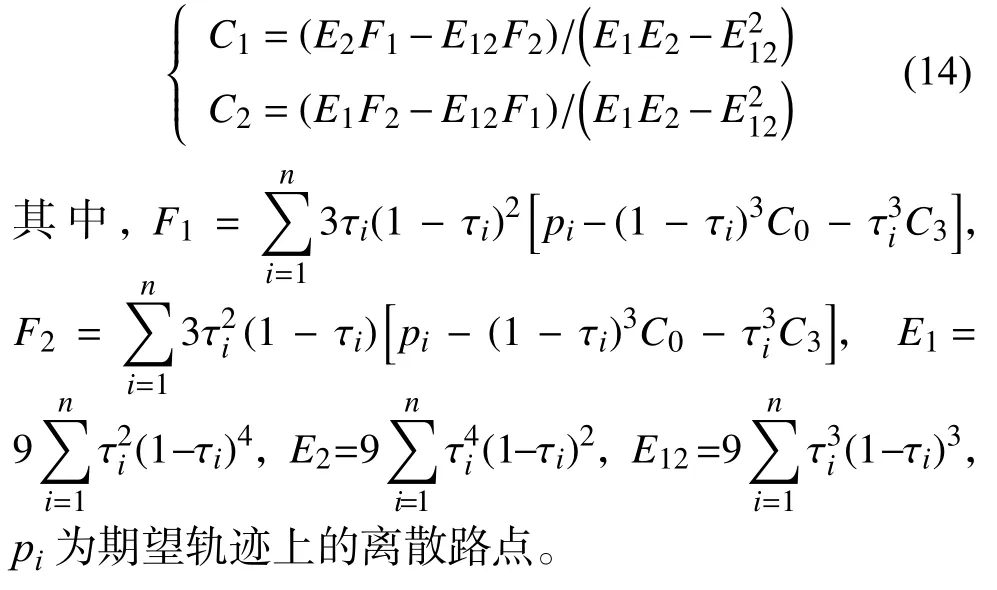
在自适应拟合的初始化阶段将期望轨迹的起止点作为三次Bezier曲线两端的控制点。每次迭代拟合分别根据式(13)和式(14)求解各段Bezier曲线的中间点以及对应的插值点,并计算插值点与原轨迹点之间的残差,并在残差最大的插值点所对应的轨迹点处将期望轨迹分段,直到拟合精度满足要求。
3.2 迭代LQR轨迹跟踪控制算法
针对半挂式车辆的轨迹跟踪控制,设计k时刻的优化性能指标为:
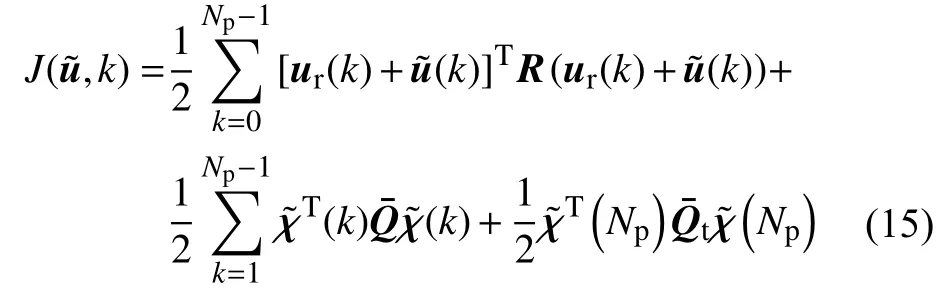
其中,Np表示预测时域,对角矩阵,t,R分 别为状态误差权重,终端误差权重和控制量权重,其对角线上的元素表示了对相应误差分量的惩罚程度。
引入拉格朗日乘子λ,式(15)可改写为最优化方程V:
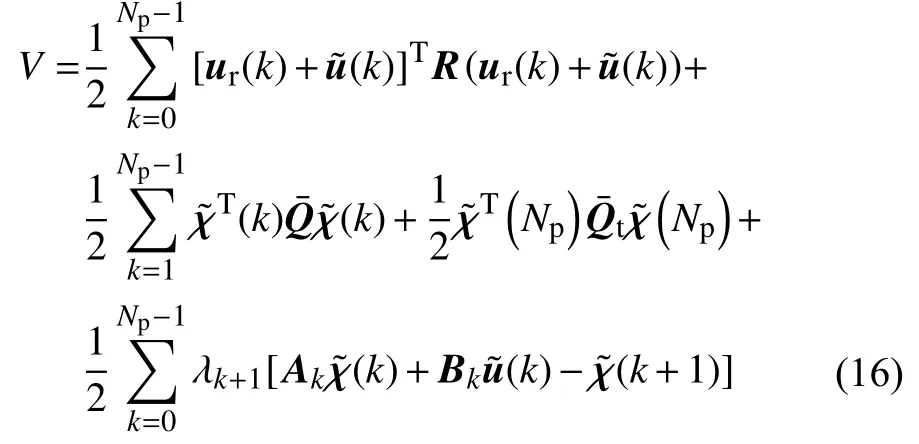
构造哈密尔顿函数,令
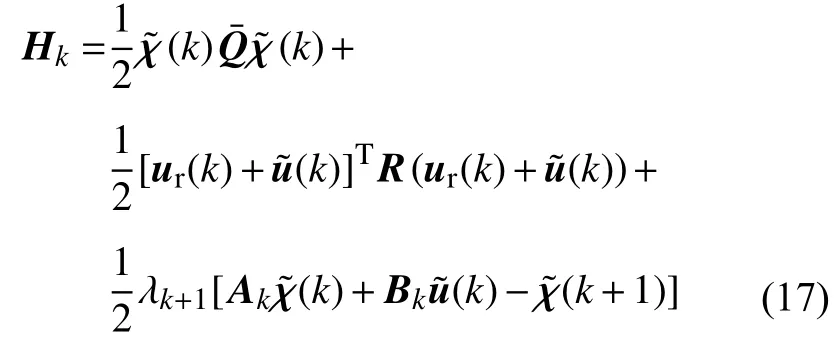
结合式(17)和式(16)可得:
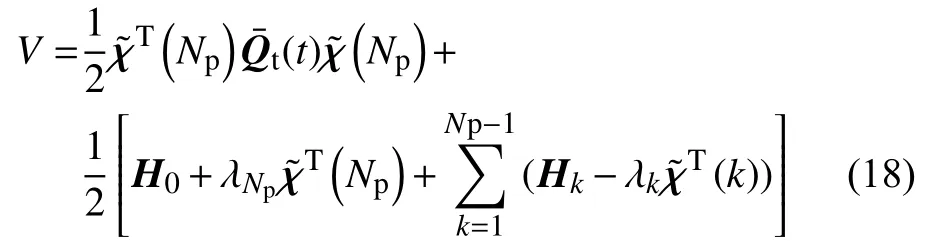
当评价函数取最小值时,函数V需满足:
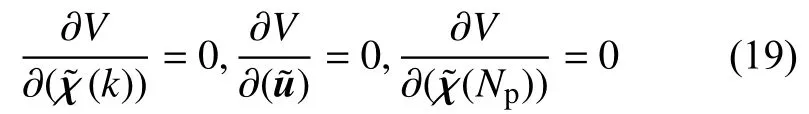
结合式(15)和式(19),根据已知的SNp=t,νNp=0和终端状态(Np),可以求得最优反馈控制量:
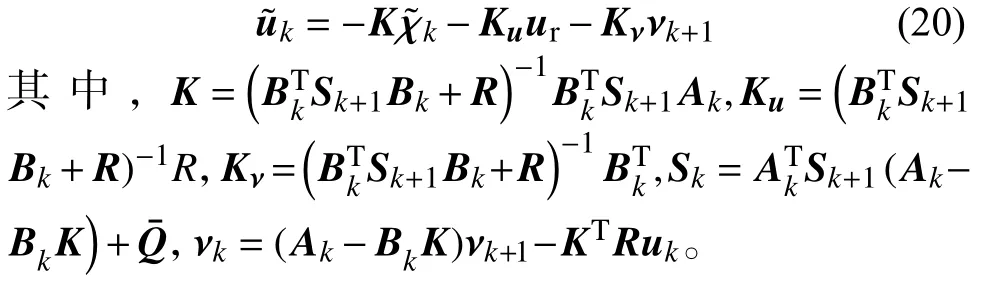
最终得到半挂式车辆最优控制控制量为:

其中,参考输入矢量ur可以通过对期望轨迹进行基于Beizer曲线的自适应拟合获得。
4 仿真系统设计与结果分析
4.1 仿真系统设计
在Simulink环境下搭建虚拟仿真平台,通过轨迹跟踪仿真实验验证本文所提出的跟踪算法的有效性。轨迹跟踪虚拟仿真平台框架如图3所示。
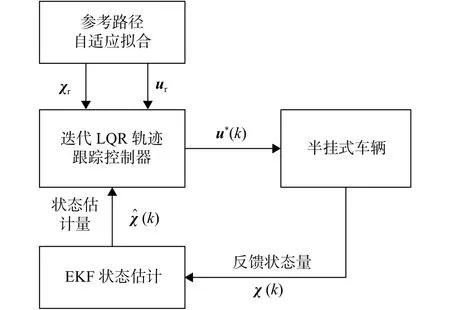
图 3 轨迹跟踪的仿真平台框架
通过非线性车辆运动模型、测量得到的车辆状态量和未来一定时间内的控制量序列可以预测车辆的状态。这是一个迭代的过程,由于控制序列不可知,就需要找到一个显式的迭代方程对微分方程进行近似求解。在工程实际中,使用较为广泛的数值解法有欧拉法(Euler method)和4阶龙格-库塔(Runge-Kutta)算法。
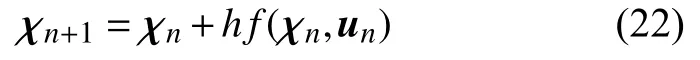
单步的欧拉法形式简单,但精度较低。为了得到较高的精度,本文采用4阶龙格-库塔算法,其一般表述形式为:
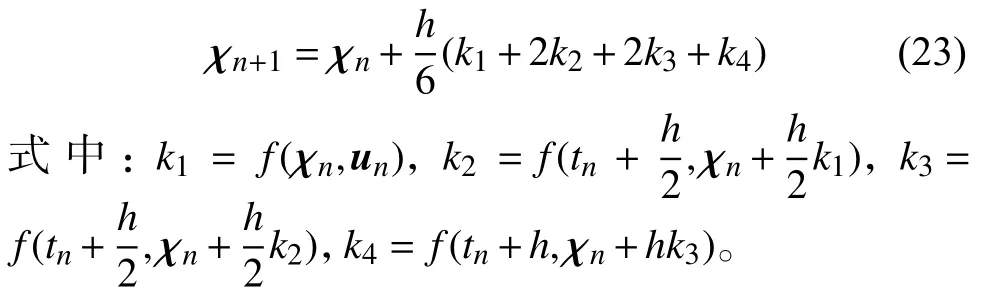
4阶龙格-库塔算法的迭代步长越小,其计算精度越高,但计算速度也会下降。
4.2 仿真结果分析
基于上节所述的虚拟仿真平台,采用表1所示的参数进行轨迹跟踪仿真实验,仿真所用的期望轨迹具有连续变化的曲率。

表 1 轨迹跟踪控制器的参数说明
首先将拟合残差的阈值β设为0.25 m,对期望轨迹进行基于三次Bezier曲线的自适应拟合,拟合结果如图4(a)所示,可以看出期望轨迹被划分为6段进行拟合,体现了自适应轨迹拟合算法的描述能力。期望轨迹的拟合残差如图4(b)所示,可以看出,拟合残差小于0.25 m,满足了满足给定残差阈值的要求。通过拟合曲线方程可以得到轨迹跟踪的前馈控制量。
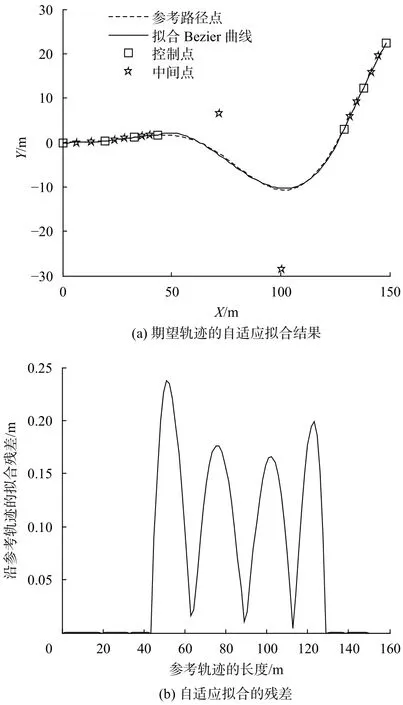
图 4 基于三次Bezier曲线的参考轨迹拟合结果
半挂式车辆轨迹跟踪的仿真结果如图5(a)所示,图5(b)为挂车中心的轨迹与期望轨迹对比,可以看出半挂式车辆能够很好地适应期望轨迹的曲率变化,到达并跟随期望轨迹。
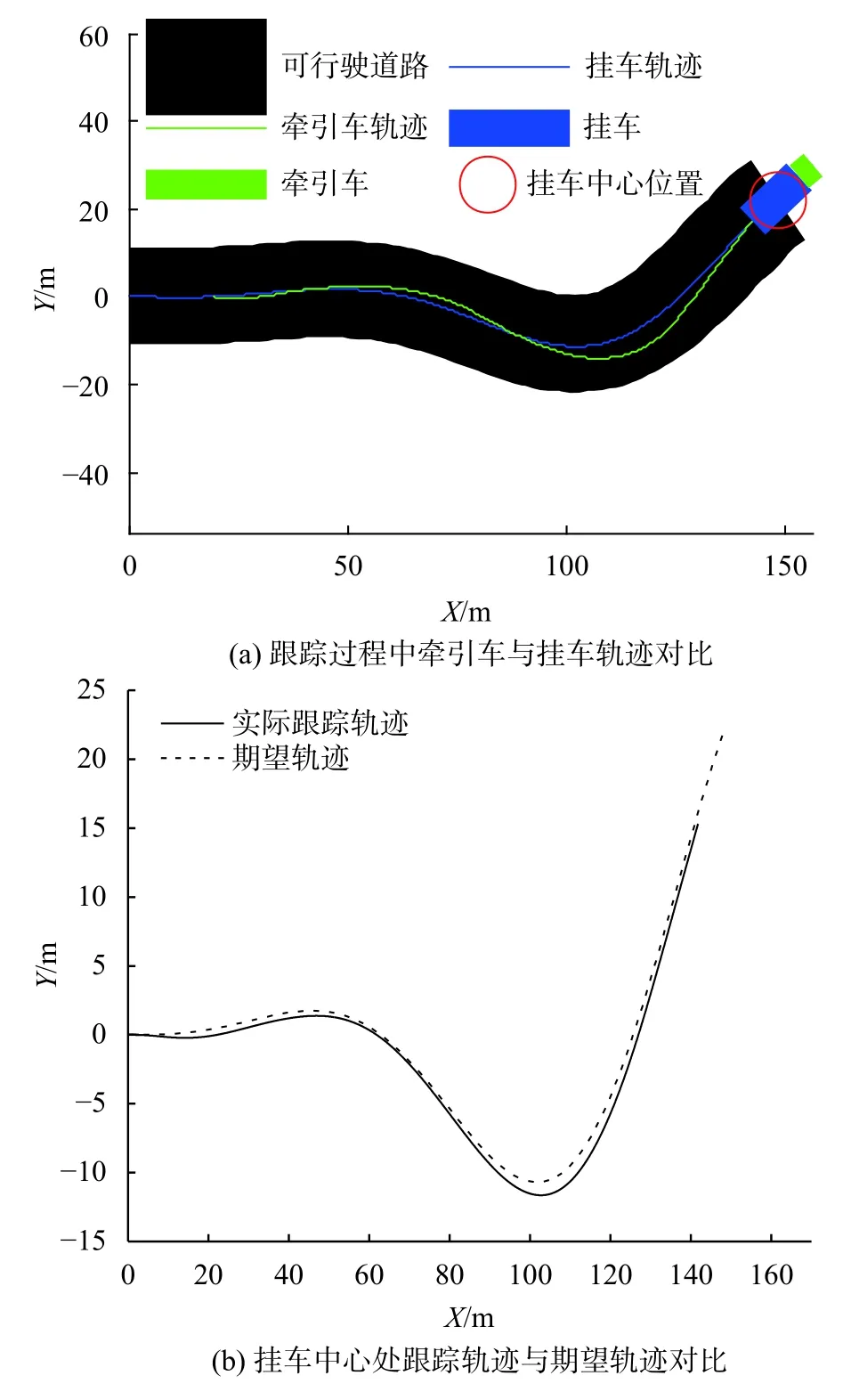
图 5 轨迹跟踪的仿真结果
轨迹跟踪仿真过程中挂车的航向角及其与牵引车之间的夹角如图6所示。可以看出挂车航向变化平滑,且挂车与牵引车之间的夹角小于0.5 rad,能够避免挂车与牵引车发生内部碰撞。
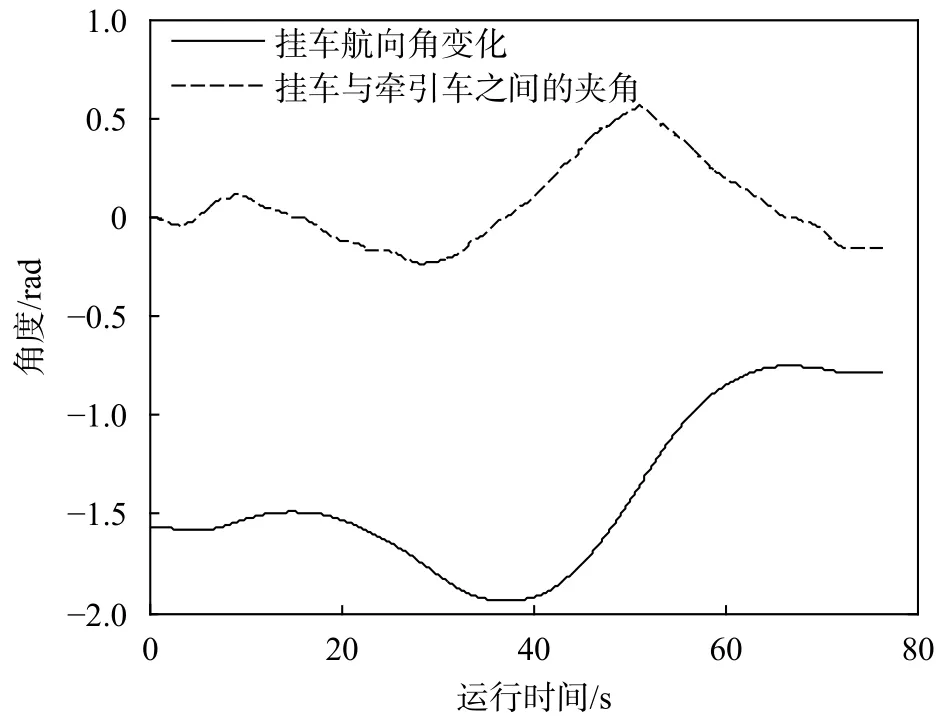
图 6 跟踪过程中挂车运动状态
在轨迹跟踪过程中,挂车相对于期望轨迹的横向跟踪偏差和航向跟踪偏差如图7所示。可以看出,半挂式车辆自主驾驶的轨迹跟踪控制器可使得挂车的横向跟踪偏差在±0.2 m以内,航向跟踪偏差保持在±0.15 rad以内,具有较高的跟踪精度。
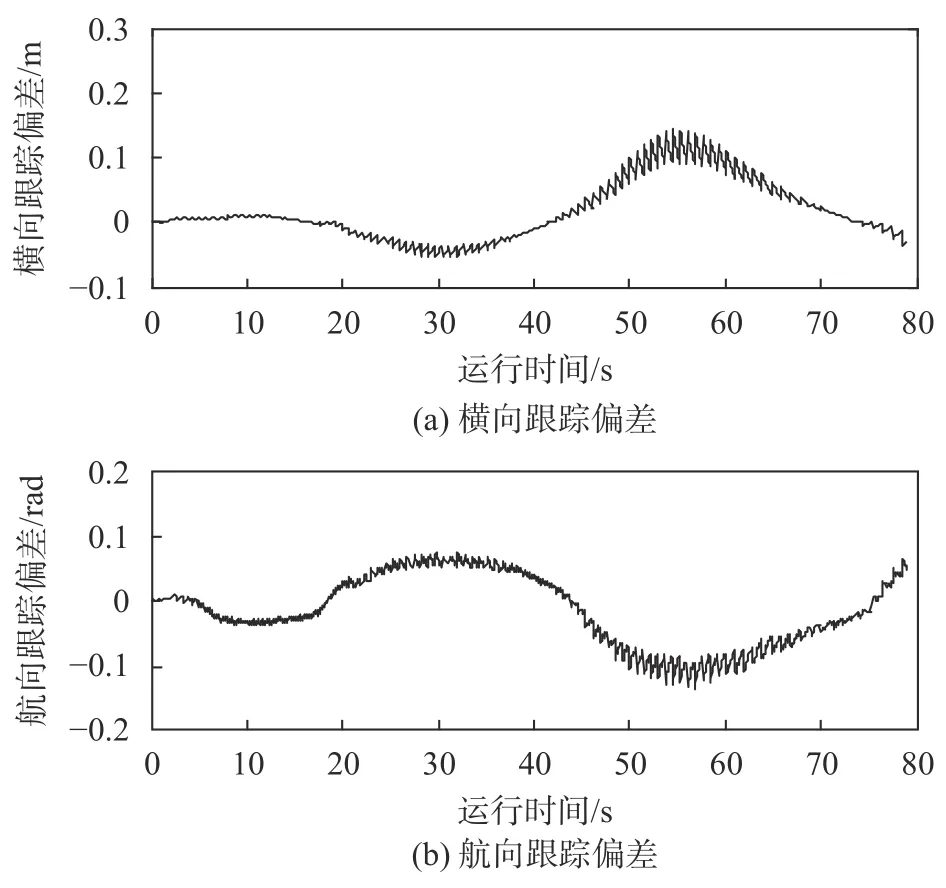
图 7 轨迹跟踪过程的跟踪偏差
轨迹跟踪过程中的控制量,即车速与前轮偏角,如图8所示。可以看出,在仿真过程中半挂式车辆的车速始终小于2 m/s,且车辆的前轮偏角控制量小于0.3 rad,满足给定的速度与前轮偏角的阈值约束。
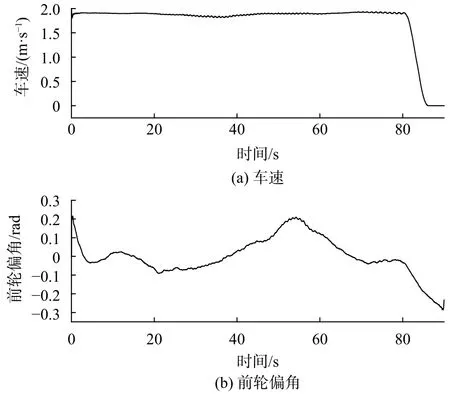
图 8 轨迹跟踪过程的控制量
从图8还可以看出,当仿真进行到80 s之后,车辆缓慢下降到0 m/s,即车辆停止。这是由于当车辆行驶80 s后已经接近期望轨迹给定的终点所造成的,当车辆到达终点后半挂式车辆停止运动。
轨迹跟踪过程中基于EKF的状态估计误差如图9所示。可以看出,半挂式车辆状态观测器对于车辆x和y坐标的估计误差在±0.2 m以内,同时对于拖车航向角的估计误差保持在-0.02~0 rad之间,满足控制精度的要求。
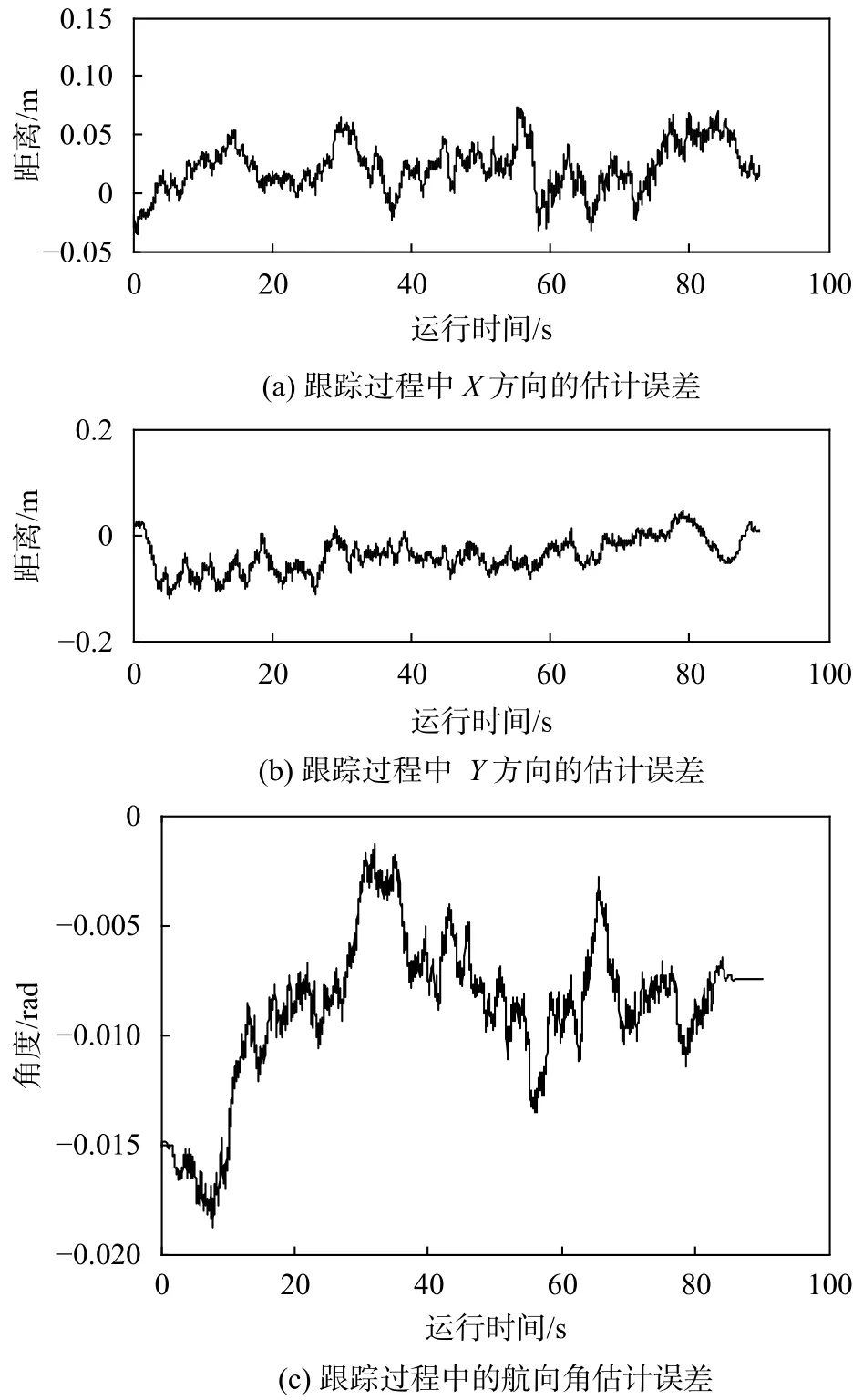
图 9 轨迹跟踪过程的状态估计误差
5 结束语
本文建立了半挂式车辆的非线性运动学模型并将其线性化得到了车辆轨迹跟踪的线性误差模型。设计了基于EKF的车辆状态观测器,有效的估计拖车的航向角。通过对期望轨迹进行基于三次Bezier曲线的自适应拟合获取了轨迹跟踪的前馈控制量。针对半挂式车辆的轨迹跟踪,设计了基于迭代LQR的控制器。仿真结果显示本文所提出的轨迹跟踪控制器能够满足半挂式车辆自主驾驶的需求。
下一步工作将深入研究半挂式车辆的动力学模型,并结合模型预测控制方法实现半挂式车辆在更高速度下的稳定性操控。

