空气耦合斜入射非线性检测方法研究

常俊杰，余 盼，罗文斌,3，钟海鹰，杨郑弘

(1.南昌航空大学 无损检测技术教育部重点试验室，江西 南昌 330063; 2.日本探头株式会社，日本 横滨 232-0033;3.中国特种设备检测研究院，北京 100029)

0 引 言

目前，超声波被广泛应用于无损检测领域。其中空气耦合超声检测因其非接触、不需耦合剂以及可在不损伤材料的情况下完成检测的优点，在实际应用中取得了很大发展[1]。虽然激光和电磁超声也可实现非接触探测，但它们对被检材料属性有一定限制，且其超声波集束的焦点与指向性难于控制而增加了检测的技术难度。空气耦合超声检测不但能够弥补这方面的不足，而且可以实现快速在线检测，具备良好的应用前景。

在一般情况下，探伤检测常采用垂直入射的方式，但由于受到试件形状和侧壁干涉等影响，在很多时候其应用就受到了限制，而且空气与常见金属（如钢、铝等）的声阻抗存在着近106级的差异，导致垂直入射时的界面损失高达45 dB，上下两个界面共损失90 dB[2]，因此在很多情况下垂直入射法并不适用。传统的线性超声检测通过时域信号对缺陷特征进行分析，当缺陷尺寸小于二分之一波长时会产生绕射波，导致信号反射和衰减等线性现象减弱[3-4]，从而难以检测出这些微小缺陷，这也反映出传统线性超声波对材料微观缺陷不够敏感的缺点。

现代国内外学者对于斜入射非线性检测方法有诸多研究，1936年Reissner从理论上推导出了纵波斜入射于浸在水中的板件的投射系数[5]；Sanders和Thomson等人通过试验证实了此理论也适用于浸在空气中的板件透射系数的计算[6-7]；非线性声学的概念在1755年被提出，自 1960年以来研究者开始利用声学的非线性特性对材料进行性能评估[8]；Hikata 等人发现了超声波在钢板中会产生谐波[9]；Sohn等基于超声非线性响应，提出了一种疲劳裂纹非线性检测方法[10]；陈振华等人对薄板点焊采用滤波技术从接收信号中获取高次谐波对微小缺陷进行更加准确地检测[11]；西安建筑科技大学宋林等人建立了在不同频率下透射系数与非线性超声系数之间呈单调递增的关系[12]。

虽然非线性检测是当前声学检测的一个热点方向，而空气耦合超声因其非接触，无损害、无损伤，易于实现自动化等优点受到了无损检测工作者的青睐，然而他们涉及空气耦合超声的非线性检测相关内容非常少。综上分析，本文将斜入射非线性检测法应用于空气耦合超声检测中，采用具有一定倾斜角度的入射超声波对钢板进行缺陷检测并将检测方式应用于微观缺陷的非线性检测试验中，最后通过数值分析与试验验证两种方法验证了斜入射条件下非线性空气耦合超声检测的可行性及高效性。

1 非线性试验原理

近年来国内外非线性声学的理论研究表明了微小缺陷非线性超声检测的可行性。非线性超声检测方式不同于以往传统线性检测，它通过分析缺陷处的频域信号来进行判别。非线性超声检测原理主要是当声波传输到试件中的损伤区域时，介质中的微小缺陷会与高能有限振幅声波产生强烈的非线性效应，发生波形畸变（产生基频波的二次及高次谐波信号），造成基波能量转移[13-14]。因不同程度和不同大小的微观缺陷所产生的非线性效应会存在差异，其二阶非线性系数也会随之变化[15]，因此，通过对超声二阶非线性系数进行分析就可以实现材料内部微观缺陷的定性。

本文将非线性声学理论和斜入射空气耦合超声检测技术相结合，应用于空气耦合的非线性检测。在试验过程中只需要捕捉到超声波遇到微观缺陷时所产生的非线性效应，进而对非线性效应进行数字化分析，就可实现对微观缺陷的检测。当单频正弦信号波在试件中传播一定距离后遇到微观缺陷而引起非线性响应时，产生的二次谐波如下式所示：

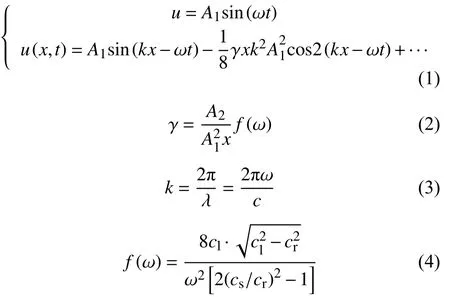
由上公式化简可得到非线性系数的表达：

式中：cl、cr、cs——纵波、横波、瑞利波的声速；

A1、A2——基频波、倍频波的幅值；

γ——声学非线性系数；

ω——频率；

文章通过设计悬垂控制器结构、摄影测量及较为有效的图像背景差分法进行图像处理，能够满足系统的实时性，将电缆位置信息转换为模拟电信号，下一步将进行算法优化，提高信号转换精度.

x——信号传播距离。

由于在同一个试件中f(ω)的值是相同的，所以本文用相对非线性系数γ'表示在不同角度下非线性系数的变化[16]，以此来评价材料损伤情况。

2 试 验

2.1 斜入射和垂直入射的对比试验

虽然空气耦合超声检测为科学研究和工业应用带来许多便利，但当试件需要以较高的灵敏度和信噪比才可检测缺陷时，垂直入射检测方式不再满足要求，图1为垂直入射与斜入射的检测示意图。其中d为钢板的厚度。

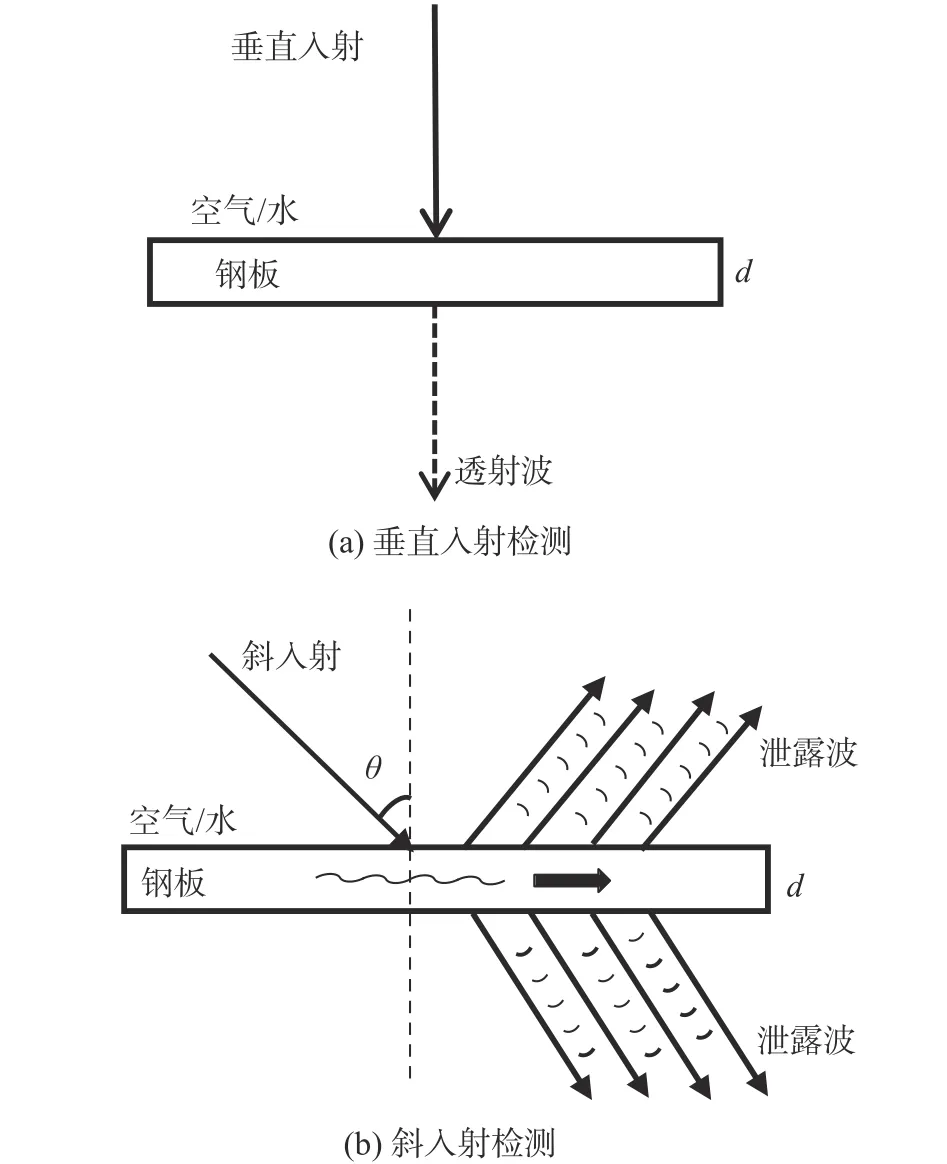
图 1 不同方式的检测方法

由表1材料参数经过计算可得到垂直入射钢板的透射情况，如图2所示。其透射率随着频厚积的改变呈周期性变化，当板厚是半波长的倍数位置时会发生全透射，且与钢板所接触介质无关。图3显示了声波在钢板中透射率对入射角的依赖关系，伴随入射角的逐渐增大，透射率在达到最高值后突然减小，此时恰对应于兰姆波S0和A0模态的临界角。

表 1 材料参数

图 2 垂直入射钢板的透射率

图 3 入射角与透射率的关系

基于以上介绍，现进行探伤检测试验，首先采用纵波垂直入射的方法进行检测，试验试件为钢板，板件尺寸为400 mm×400 mm×3 mm。发射与接收探头为空气耦合超声探头，晶片尺寸为20 mm×14 mm，频率400 kHz。在试件上下两侧的同一垂线位置处各固定放置一个空气耦合超声探头，上端为发射探头，下端为接收探头，且此试验装置可以调节探头的角度位置，为后面斜入射检测试验提供方便。超声发射接收器对其施加300 V的电压，经内置带通滤波器滤波和外置信号放大器对信号增幅后由接收器接收并显示信号波，整体试验系统如图4所示。调整两探头之间的纵向距离至18 mm，使探头与试件水平面垂直，随后逐渐调整入射角，角度每增加1° 采集一次信号波，其中当垂直入射与入射角为8°时分别采集到的试验信号如图5所示。

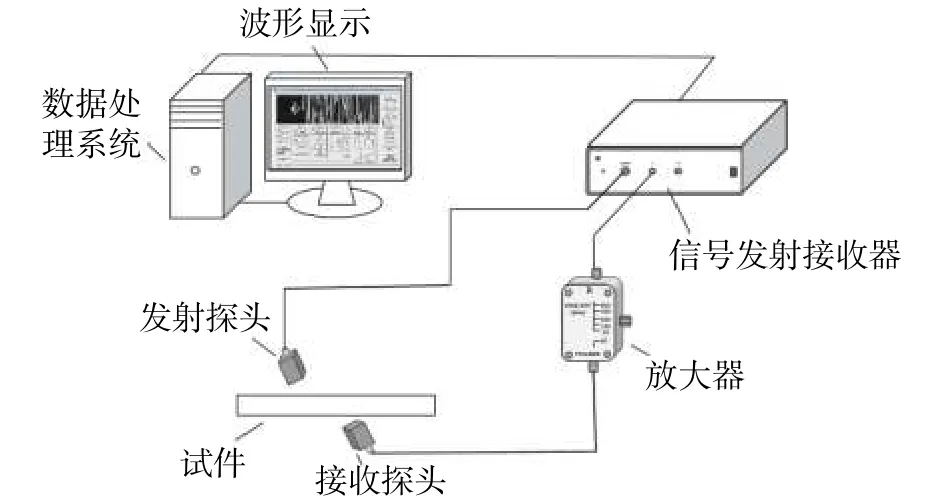
图 4 试验装置系统

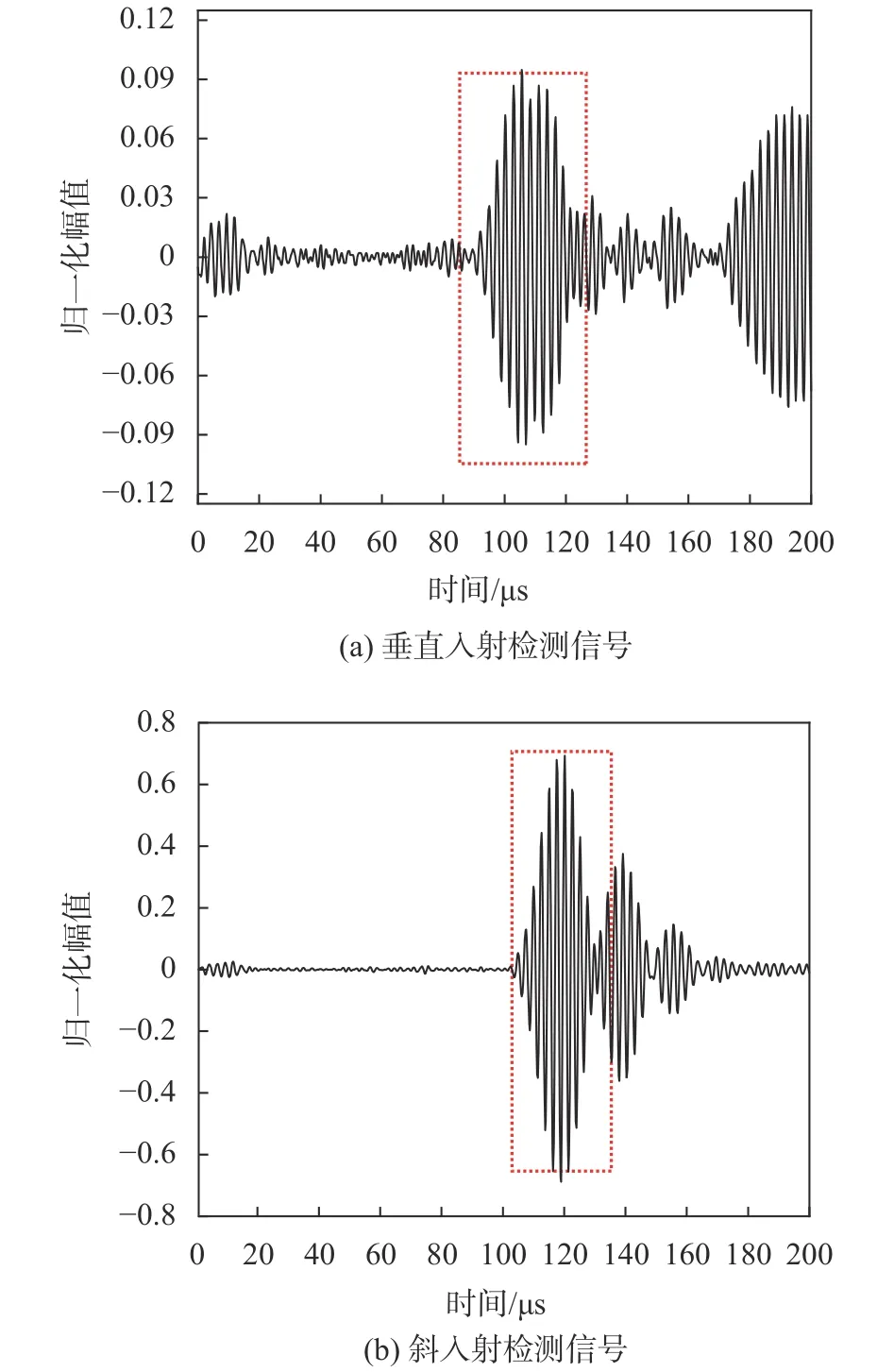
图 5 试验检测信号

图 5（a）和图 5（b）分别是入射角为 0°和8°时的数据采集结果，其归一化幅值对应于0.1和0.7。从两幅图的对比中可以发现因入射角度的改变，导致检测结果存在明显差异，且在入射角为8°时，检测效果更好。试验采集了16组数据，结果如图6所示。从试验结果发现，无论检测试件是否存在缺陷，透射波信号值均会随着入射角度的改变呈先增大后减小的总趋势，且在8°附近时峰值达到最大，即透射率最高。

图 6 钢板试验检测数据结果

由图7频散曲线图得到在频厚积为1.2 MHz·mm时A0模态所对应的相速度为2 469 m/s，根据Snell定理得出此时的临界角为7.92°，恰好对应于试验中在入射角为8°时得到最大透射率的情况。试验证明，在斜入射条件下超声波在传播过程中可能会发生模态转换而导致透射率增大。

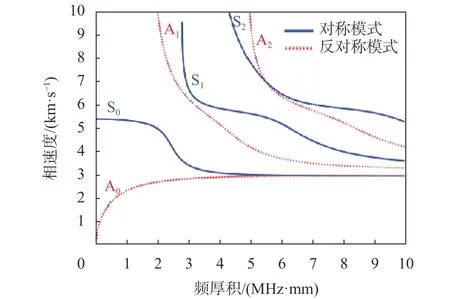
图 7 频散曲线

试验中虽然通过试验装置较精确地调整了角度，但通过采集的实际数据结果显示并未达到A0模态临界角处的全透射以及S0模态临界角附近的较高透射率。这是由于试验设备发射接收的信号波并不是理想简谐振动，而是带有一定频宽的信号波，并且由于空气耦合探头的晶片尺寸有限，其产生的声场也不是理想平面波，以上各原因导致试验结果与理论计算的结果存在一定误差。基于以上验证，在非接触空气耦合无损检测应用中，斜入射检测可以提高超声波的透射率。本文进一步对空气耦合超声非线性检测微小缺陷及入射角度产生的影响进行探讨。

2.2 非线性检测微损伤试验

试验材料为A316L型奥氏体不锈钢，试件经过0.5 h的1 100 ℃高温热处理，使之造成高温疲劳损伤而产生微观缺陷。热机械疲劳加工是由机械和温度循环叠加完成，通过IN ST RON液压伺服试验机实现机械循环，由抛物线内壁灯和加热炉实现温度循环，加热完毕后以自然对流的方式进行温度冷却，经由以上工序加工试件内部形成了微观缺陷。试验选择Japan Probe公司生产的超声发射接收器JPR-600C（为了发射宽频带的超声，发射波形为线性调频波），设置调频比为200%、中心频率1 MHz、波数为8，发射波形如图8所示。使用发射探头为1 MHz的空气耦合超声平探头，接收探头为2 MHz的空气耦合超声平探头。采用垂直入射与斜入射两种检测方式进行试验，试验方法与上述试验相同，每间隔1°采集一次数据。

图 8 发射波形（线性调频波）

2.3 结果分析

选择有限幅度法，通过高能输出单一频率的大振幅超声波，使得波在材料传播中与缺陷相互作用产生波形畸变，形成高次谐波，最后对接收到的信号进行频谱分析得出基波和高次谐波的幅值。图9为在垂直入射和斜入射角为5°时分别检测到的信号波，用Matlab对时域信号的标注部分做傅里叶变换得到图9（b）和图9（d）两幅频谱图。对比发现，在斜入射情况下时域接收信号幅值增大24%，二次谐波幅值由0.018 2变为0.047 7，提高了162%。

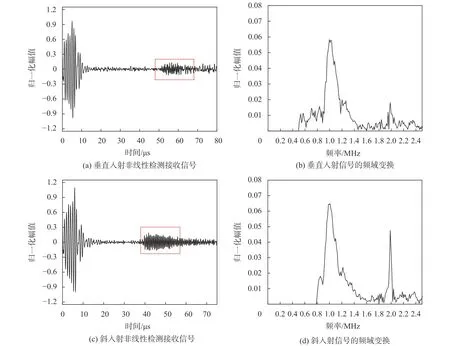
图 9 非线性空气耦合超声检测

由式（4）获取在每个角度下所对应的相对非线性特征参数，用以评价材料的微小缺陷。试验数据结果如表2。由表可知在斜入射条件下，检测信号的基频幅值基本没有发生变化，而倍频幅值出现先增大后减小的总趋势，并且当入射角为5°时非线性检测信号倍频幅值达到最大。由图10可明显看出随着斜入射角度的逐渐增加，二阶非线性系数同样呈现先增大后减小的总趋势。入射角在0°～5°的范围内相对非线性系数递增，即检测到缺陷处产生的非线性响应愈加显著。因为透射系数与非线性超声系数之间呈单调递增的关系，所以试验有效验证了以斜入射的方式应用于非线性检测微观缺陷时可以提高超声波的透射率和检测灵敏度。

表 2 频谱数值及相对非线性系数

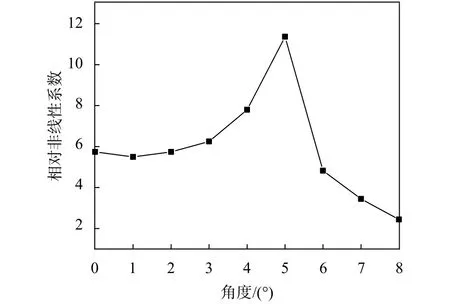
图 10 入射角度与相对超声非线性系数的关系

3 结束语

通过以上空气耦合斜入射与非线性超声检测试验，分析得出以下结论：

1）纵波垂直入射钢板的透射率随着频厚积的变化呈周期性改变，当板厚是板材料纵波半波长的倍数时可发生全透射，这与试件所接触介质没有任何关系。

2）以斜入射检测方式用于检测缺陷比普通穿透法更容易得到波形清晰、幅值更大的信号。由斯涅尔定律的相位匹配条件，声波发生模态转换且入射角度在对应于兰姆波A0模态的临界角时检测信号最佳。

3）当缺陷尺寸为微观缺陷时,可利用空气耦合超声非线性检测方法进行检测，且在斜入射条件下能够得到更佳的二阶非线性系数，提高信号的透射率和非线性检测的应用范围。