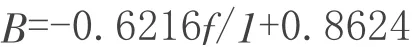大跨度拱桥拱肋顺桥向风荷载计算方法研究

谭卜豪

(广东省交通规划设计研究院股份有限公司)

0 前言

随着科学技术的发展，我国及世界桥梁建设得到了快速发展。我国西部大开发以及一带一路建设，西部地区将架设更多的交通设施。由于我国西部地区多为山区丘陵地带，需要修建许多跨越峡谷的桥梁，将天堑变通途。拱桥因其不需要在峡谷中落墩的优势，成为跨越山区峡谷的首选桥型。也因其优美的曲线，常常成为城市景观桥梁的主要选择类型。比较有名的拱桥，例如，主跨552m 中承式系杆拱桥中国朝天门大桥、主跨550m 中承式系杆拱桥中国卢浦大桥、主跨420m 中承式系杆拱桥重庆菜园坝大桥[1]、近年来有主跨436m 中承式连续钢桁拱桥明珠湾大桥。随着拱桥跨度的不断突破，风荷载的作用将越来越明显，在设计计算时需要设计人员更加关注抗风设计理论和相关技术。

目前《公路桥梁抗风设计规范》[2]中，主要针对梁桥、斜拉桥、悬索桥做了相对细致的要求，但是对拱桥的相关验算与规定还比较少。

1 研究背景

以某大跨度中承式钢管混凝土拱桥为研究对象，如图1 所示。全桥跨径组合为6×25m 小箱梁+388m 中承式钢管混凝土拱桥+5×25m 小箱梁。主拱肋采用四肢桁式钢管混凝土结构，净跨径360m，计算矢跨比为1/4，拱轴系数为1.55。双片拱肋中距31m，肋宽4m，拱顶桁高6.5m，拱脚桁高12m。桥宽32.2m，吊杆间距为15.2m。主拱主管钢材采用Q390qD，其余钢材采用Q355D。双片拱肋之间采用“△+I”形式横撑。主梁采用格子钢梁叠合22cm 混凝土的组合结构。

由于所在区域基本风速很大，换算到桥面上风荷载比较大，需要对主桥进行详细的抗风验算。

2 提出问题

图1

在进行风荷载计算时，根据《公路桥梁抗风设计规范》主要规定了主梁横桥向风作用下等效静风荷载Fg，与主梁顺桥向等效静风荷载作用Ffr，以及桥墩、桥塔、斜拉索、主缆、吊杆的等效静风荷载。但是对拱肋结果的计算方法，并没有提及，根据其形式特点可仍按照主梁相同方法进行计算，但是其中还是存在较大区别。在计算中遇到的最大问题是：相比主梁结构，主拱圈形式为曲线抬升的结构，其顺桥向等效静风荷载是否与主梁一样仅采用摩擦力进行计算。

3 理论分析

顺风向风速作用在斜面上取一微段进行分析。其中Ug为等效阵风风速。其可以分解为平行于拱肋的风向，和垂直于拱肋的风向，可以分别考虑其为结构提供风荷载的情况。

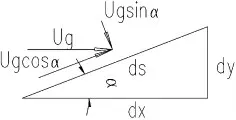
图2 风速矢量分解

垂直于拱肋方向风速提供风阻力可以通过主梁横桥向风荷载作用下等效每延米静风荷载计算，如式⑴所示。

其中，

Fg——每延米阻力；

ρ——空气密度；

CD——阻力系数；

D——结构宽度。

平行于拱肋方向风速提供风阻力可以通过主梁顺桥向风荷载作用下等效每延米静风荷载计算，如式⑵所示。

其中，

Frf——米延米摩擦力；

Cf——摩擦力系数；

s——主梁周长。

对拱肋微段进行受力分析如图3 所示。

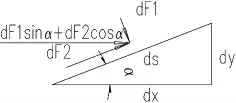
图3 拱肋受力分析

其中，dF1为微元体上垂直于拱肋作用，dF2为微元体上平行于拱肋作用力计算公式如下。

其中，Fx——拱肋水平荷载。

根据上述结果建立拱肋曲线坐标系与对应坐标系的悬链线方程[3]：坐标系如图4，根据函数关系可以推导如下公式：

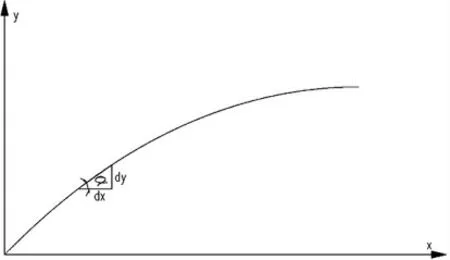
图4

其中，f 为失高，m 为拱轴系数，k=cosh-1（m）。

式⑺、式⑻联立方程组可得：

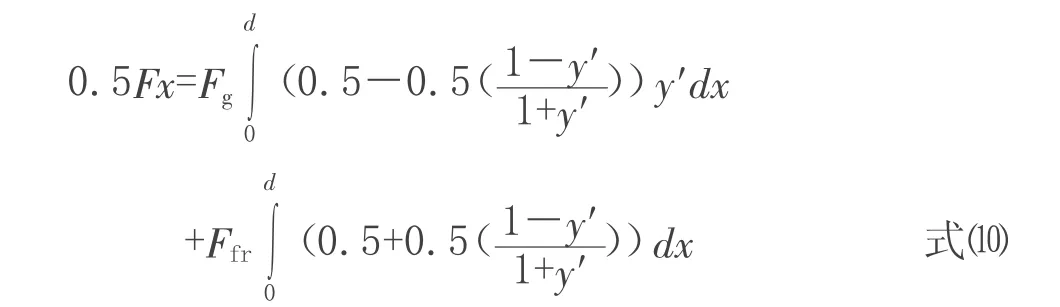
即式⑴、式⑵、式⑼、式⑽联立可以求解顺桥向风荷载的理论解。

4 应用实例

通过上述计算过程，对某大跨度拱桥拱肋顺桥向风荷载进行计算。首先通过MATLAB 程序计算式⑼悬链线方程，其计算结果如图5 所示：与拱桥曲线一致。倒数曲线即为tanα 随x 变化曲线，由图6 可知其计算结果与理论分析结果一致。由此验证MATLAB 程序计算结果的正确性[6]。

拱肋断面形式为如图7 所示：根据当地气象数据转换设计风速为Ug=54.57m/s：顺桥向拱肋宽度D=4m，根据规范计算可知，平均单片阻力系数CDs=0.64；两片为CD=1.28；拱肋周长s=21m，摩擦系数Cf=0.065。根据式⑴、式⑵可以计算得到Fg=10060N/m；Ffr=2683N/m。

根据公式⑽计算可知，一半拱肋上作用水平向风荷载0.5Fx=756180kN。一半拱曲线长度根据下式计算，计算结果为S=220m。

拱肋单位长度顺桥向风荷载fx=Fx/S=3670N/m。比较fx与Ffr和Fg可知，用阻力作为拱肋单位长度顺桥向风荷载计算结果过于保守，而用摩擦力计算结果作为顺桥向风荷载结果则偏于不安全。

为了定性分析拱肋上阻力与摩擦力出力的不同情况，做如下定义：

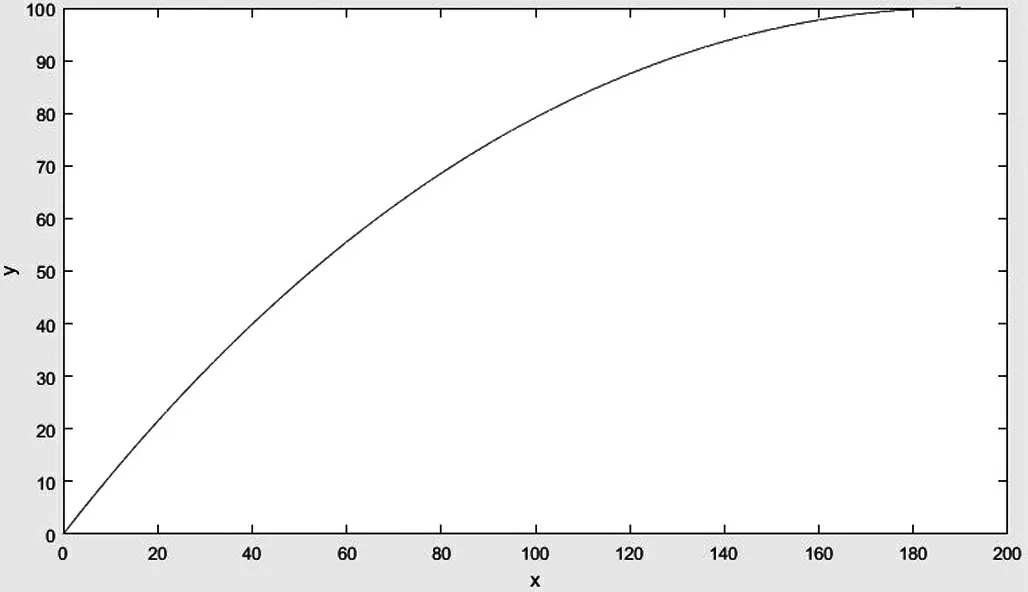
图5 悬链线方程曲线

图6 悬链线倒数方程曲线

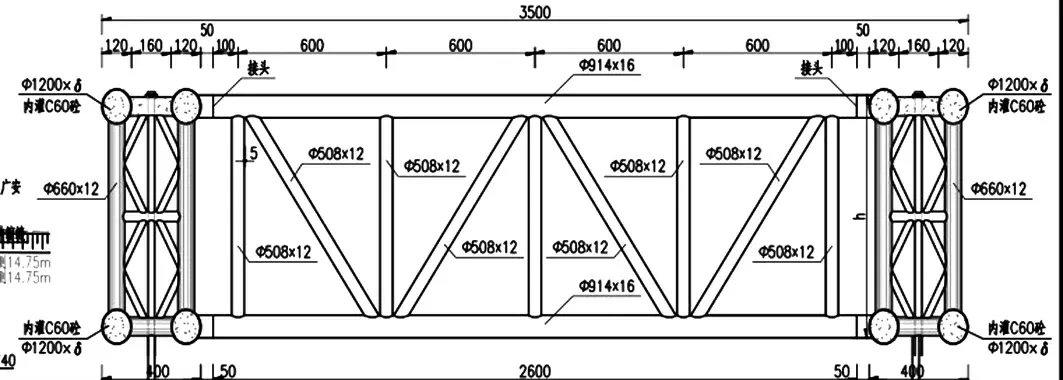
图7 标准横断面

计算可知本工程实例中A=0.4038，B=0.6862，由此可以将拱桥顺桥向风荷载简化为墩高f、长度为l 的门式刚架顺桥向风荷载，但是需要乘以折减系数。由A、B公式可知，其仅仅是拱轴线系数m、矢跨比f/l 有关的参数。

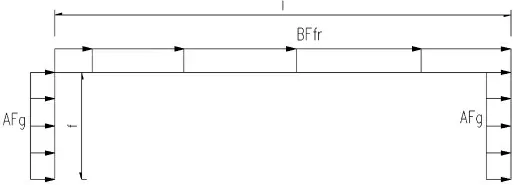
图8 等效门式钢架受力模式

5 参数敏感性分析

5.1 拱轴线系数

控制矢跨比不变为0.25，大跨度拱桥常用拱轴系数为1.05～2[6]。在此范围内计算阻力折减系数A 与摩擦力折减系数B 随拱轴系数变化关系，计算结果如图9所示。由图可知，参数A、B 随拱轴系数m 的增大而略有增加，但是增加幅度可以忽略不计。

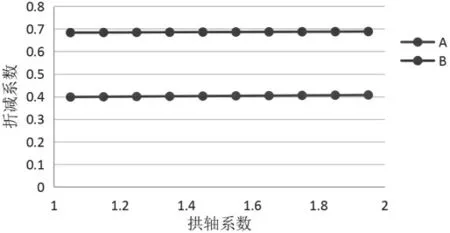
图9 拱轴系数与折减系数关系图

5.2 矢跨比

控制拱轴系数为1.55 不变。大跨度拱桥常用矢跨比为0.15～0.5[6]。在此范围内，计算折减系数A 与摩擦力折减系数B 随矢跨比变化关系，计算结果如图10所示。由图可知，随着矢跨比的增加阻力折减系数在增加，取值范围在0.25～0.6 之间，基本呈线性增长；摩擦力折减系数随矢跨比的增加而减小，取值在0.8～0.5之间，基本呈线性下降，由此可以拟合得到折减系数A、B 的计算公式：

图10 矢跨比与折减系数关系图

6 结论

⑴提出了顺桥向风荷载计算模型并得到了悬链线拱桥顺桥向风荷载理论公式。

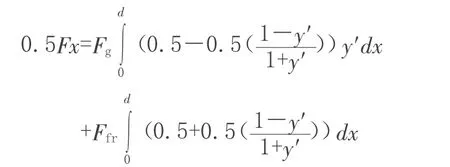
⑵证明仅仅考虑摩擦力的顺桥向风荷载比理论计算出的顺桥向风荷载小了接近30%，存在较为严重的偏差。

⑶提出了含有阻力折减系数A 与摩擦力折减系数B 的类门式刚架拱桥顺桥向风荷载计算方法：

0.5Fx=FgAf+FfrBl1

⑷根据参数分析，A、B 参数只与拱轴系数和矢跨比有关；

⑸阻力折减系数A 与摩擦力折减系数B 随拱轴系数m 的增大而略有增加，但是增加幅度可以忽略不计。

⑹随着矢跨比的增加阻力折减系数A 在增加，取值范围在0.25～0.6 之间，基本呈线性增长；摩擦力折减系数B 随矢跨比的增加而减小，取值在0.8～0.5 之间，基本呈线性下降，其线型拟合结果如下：

A=0.7283f/1+0.2014