水平搭载的剖面漂流浮标型线优化设计研究
任万龙,郝宗睿,王 越,刘 刚,华志励
齐鲁工业大学(山东省科学院) 海洋仪器仪表研究所,青岛 266001
在海洋科学研究中,自持式剖面漂流浮标(ARGO浮标)是一种常用的海洋监测及气候预报的科研平台,通常其采用垂直释放的模式[1]。随着研究的发展,自持式剖面漂流浮标需要通过航行器搭载,运行至指定地点定深投放,从而探测指定地点的海洋环境。ARGO浮标常见结构形式是球形结构[2]、柱体结构[3]、柱球一体[4]等,这些结构形式的浮标均适用船上抛载投放,不适用于水下搭载运输投放。上述浮标结构为不规则结构体,局部存在较大的凸起,在水平搭载运输过程中极易诱发不稳定流动,产生非线性涡旋结构,一方面增加航行阻力,一方面增加了水平搭载的不稳定性因素[5]。上述几种结构中,柱形浮标较为适合进行水下搭载投放。因此,本文以柱形浮标为原始模型,在不改变浮标原始尺寸的前提下,对柱形浮标外部结构型线进行修正,从而使其满足需求。
本文基于水下航行器的流线型外形,对原始柱形浮标提出三种改造方案,采用数值计算的方法,分析三种型线的阻力性能及其造成的流场特性,对比局部涡旋结构演化,结合速度分布及压力分布,确定符合水下搭载需求的型线,以减小浮标搭载航行的阻力,节省航行器能源,便于深远海投放。
1 模型介绍
1.1 湍流模型
采用流体分析软件,进行浮标改造方案的性能计算。在标准k-ε的基础上,还有多种改进的湍流模型[6],其中比较常用的是RNG k-ε模型和Realizable k-ε模型。文中选取RNG k-ε二方程湍流模型来封闭RANS方程[7]。
其控制方程如下:
(1)
(2)

1.2 型线模型
常用的回转体流线型有Mring曲线、格兰韦尔线型、卡克斯线型等[8],本文采用常用的Myring曲线作为基础型线[9],进行浮标外壳的优化。Mring线型的头部曲线方程为:
(3)
尾部曲线方程如下:
(4)
式中,a为首部长度,b为平行中体长度,c为尾部长度,d为平行中体直径,n为锐度因子,θ为去流角(单位弧度);aoffset为首部长度修正值。
2 模型修改及网格划分
2.1 修正模型分类
原有的浮标结构整体结构呈柱状,如图1 a)所示。局部表面由于功能性的设计需求具有多处凸起结构,在水平搭载航行中易产生涡旋结构,从而导致阻力增加。结合低阻流线的设计需求,利用Myring曲线对浮标外部凸起结构进行局部修改,获得三个修正型,如图1 b)至d)所示。

注:a)原浮标结构;b)方案1;c)方案2;d)方案3
2.2 网格划分
采用ICEM软件实现浮标模型网格划分工作,通过其强大的功能和可视化操作,对浮标原始模型及3种修正方案进行网格划分[10]。考虑计算模型的表面区域非规则体,选择非结构网格划分方法,对浮标表面进行加密处理,以便捕捉标体表面的流动,准确计算标体运动情况。计算域为一个包围浮标的圆柱体,半径为2倍体长,保证边壁不会影响标体的流动,使其充分扩散;计算域入口距离浮标头部3倍体长,出口距离浮标尾部6倍体长,以确保来流和尾流充分发展。计算域入口设置为velocity-inlet,出口设置为outflow,边壁设置为无滑移边界条件。为保证计算计算精度,对标体表面进行加密处理,以获得精确的计算结果。计算域及标体网格如图2所示。
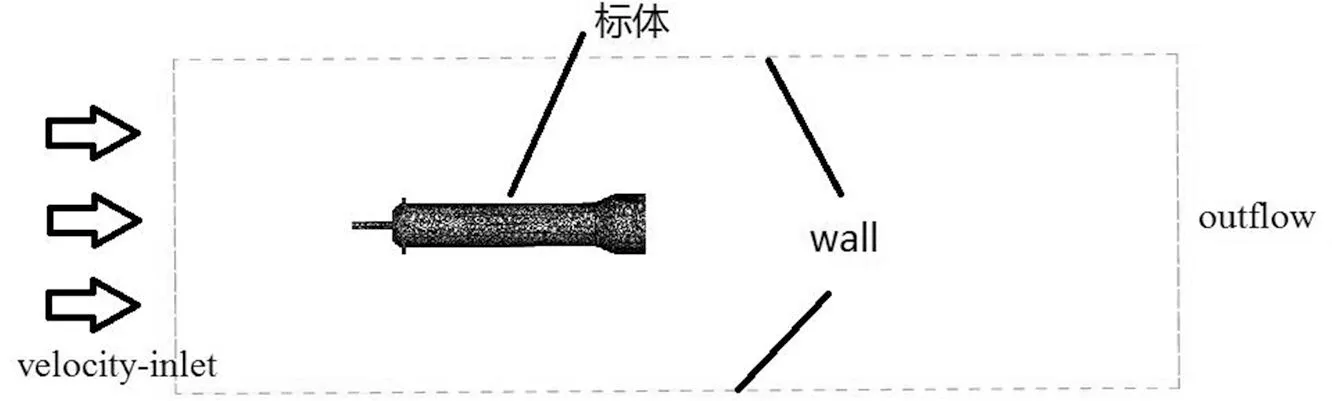
图2 计算域及标体网格
2.3 网格无关性验证
考虑到数值计算过程中,网格的质量会影响计算结果,本文以浮标在2 kn时的阻力预测值变化小于5%作为网格相关性验证,网格总数分别为28万、50万、80万,网格质量均在0.3以上,满足网格质量要求。网格无关性检查如表1所示。从表中可以看出,case 2和case 3的阻力误差均小于5%,考虑计算成本,选择case2作为最终计算网格。计算网格数量为38万,节点数为6万。

表1 网格无关性检查
3 结果分析
3.1 速度场分析
数值计算完成后,选择中纵剖面,获得各个剖面的速度云图如图3所示。从图中可以看出,原标体拖着距离较长的尾流,尾流内涡旋结构复杂,严重耗散了浮标水平航行的能量;而方案1的速度场分布比较均匀,速度波动较小,流域内极大值速度小于其他方案;方案2的速度场在尾部产生明显的速度梯度,且区域范围较大,且具有较长的尾流,较原始模型小的多,但仍会耗散部分航行能量;方案3在首部位置和尾部位置产生与方案1相似的速度梯度分布,其速度分布与方案1类似。从图中可以看出,导流壳的安装有效的避免了浮标局部凸起的引起的不稳定绕流,将流动平稳过渡,从此来看,导流壳的安装有效的减少水平搭载的阻力。

图3 速度云图
图4为原始模型与不同改造方案的涡量分布。从图中可以看出,原标体的首部盘状结构处,涡量值较大,由此判断产生大量的涡旋结构,同时尾部也具有明显的涡量分布,形成两道尾涡,大量涡旋结构的产生消耗了标体航行的能量。方案1整体的涡量分布较为均匀,在尾部位置具有涡量分布,产生了局部小的涡旋结构。而方案2在首部两侧具有明显涡量分布,意味着产生了强度较大的涡旋结构,向标体两侧扩展;尾部由于是个截平面,形成钝体绕流,两侧也对称分布着涡量,诱发交替的涡旋结构脱落,向后方延伸。方案3由于其处理上与方案1类似,仅在平行中体出有所差别,因此,整体涡量分布与方案1类似,在头部收缩位置和尾部扩散位置具有较大的涡量值。

图4 涡量对比图
3.2 压力场分析
图5为三种不同方案表面压力分布与原标体对比。从图中可以看出,原标体的头部呈盘状结构,严重阻碍水流,其压力较大,盘状结构后边形成绕流,出现低压区,而在尾部结构处由于标体结构缺少平缓过度,形成凸起同样因为绕流,在前方形成高压区,凸起后侧为低压区;方案2压力较高的位置是在首部收缩和尾部扩散处,方案3的首部压力较低,首部收缩和尾部扩散的位置与方案2的变化趋势一致,这是由于这两种方案的结构形式所致。而方案1的压力分布最为均匀,压力整体没有明显的高低交替的位置,这也代表方案1的附近很少出现涡旋结构,流线整体变化较为平坦。从标体表面的压力分布来看,通过流线修改,可以有效的改善其压力分布。在压力分布方面,方案1的优化策略优于其他两种方案。

图5 压力分布
图6为标体中纵剖面处压力分布。图中可以看出,原标体的压力分布均值较大均高于其他优化方案,且在首部和尾部等局部结构压力差较大,与前面压力分布相对应;方案1的压力分布较为均匀,仅在首部尾部位置存在较大的压力变化,整个平行中体位置压力分布较为均匀,在首尾两侧由于筒体直径的变化,导致压力出现抖动;方案2和方案3由于伴随标体进行局部改造,在局部改造的位置存在较大的压力脉动变化。从图中也明显看出,尽管方案3的压力突变也有,但是其整体压力分布较低,与图5压力分布相对应。
3.3 阻力分析
通过对原模型及三个优化方案的阻力计算,获得阻力计算结果,如图7所示。从图中可以看出,在2~4 kn的航速内,原标体的阻力最大,优化方案的阻力明显小于原标体阻力。方案1的阻力比原标体减小了84%,方案2的阻力减小了51.8%,方案3的阻力介于方案1和方案2之间,其阻力减小了77%。三种方案中,方案1的改动最大,其效果最为明显,方案2的改动最小,其阻力减小最少,而方案3的改动仅比方案2多一个尾部的结构,但其减小的范围与方案1类似。随着航速的增加,优化方案的阻力减小更多,以方案1的阻力减小最为明显。在低航速范围内,随着航速的增加,阻力增加有限。
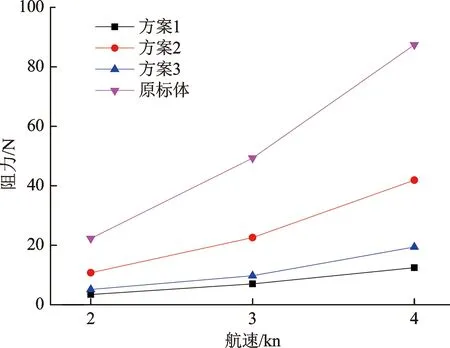
图7 阻力曲线
3.4 偏转力分析
浮标在被搭载下行过程中,会受到偏转力矩的作用,考虑浮标搭载下行过程中,主要是以某和速度下行。本文以水平航速不变,增加垂向速度,分析其不同方案下的偏转力和偏转力矩,具体结果如图8至9所示。
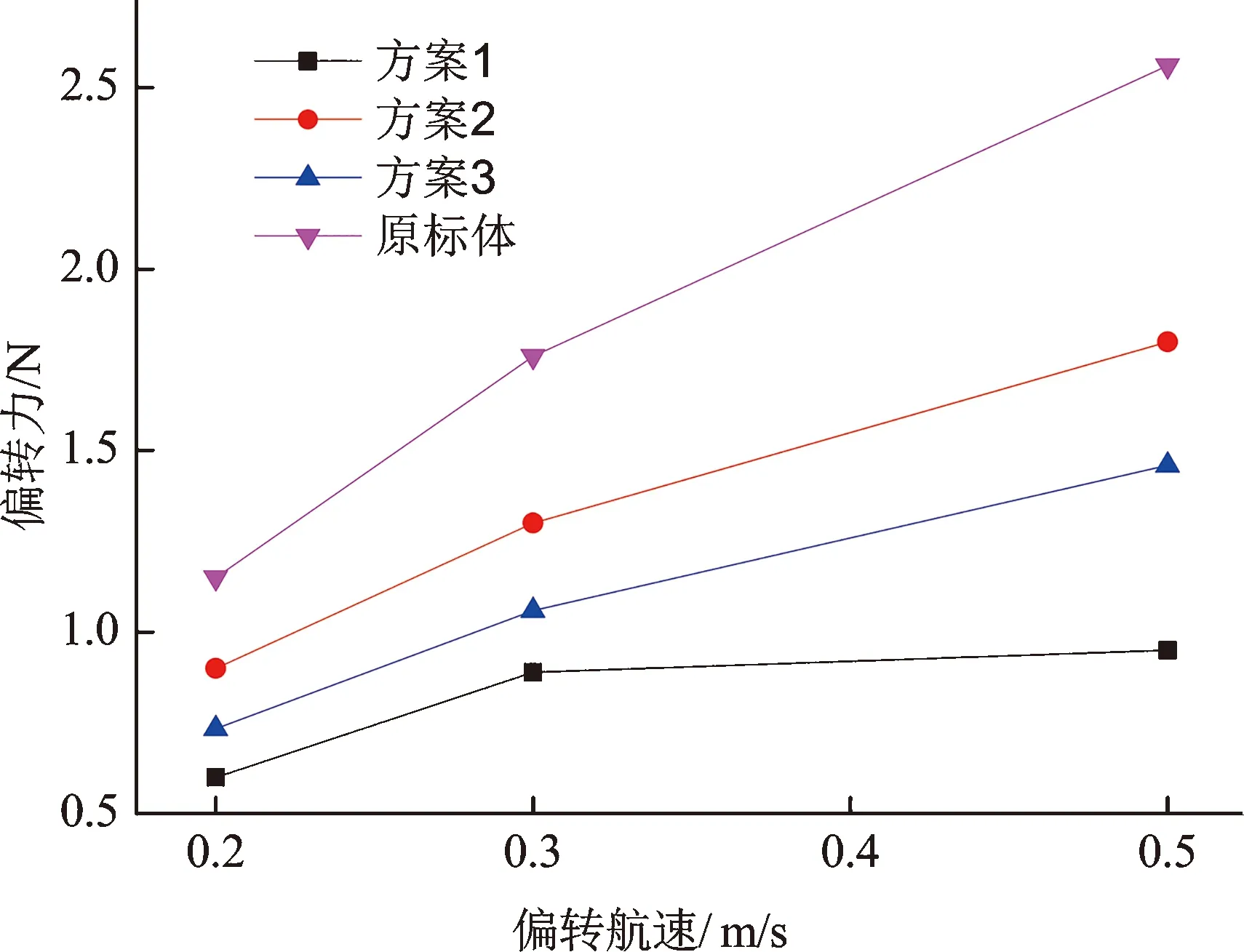
图8 偏转力分析

图9 偏转力矩分析
通过计算,发现无论是偏转力矩还是偏转力,优化方案的偏转力和偏转力矩都减小。在偏转速度为0.3 m/s时,其中方案1的偏转力比原标体减小47%,偏转力矩减小57%;方案2和方案3都减小,其中,方案2减小最少,偏转力为25%,偏转力矩减小48%。而方案3的偏转力和偏转力矩介于方案1和方案2之间。从中可以看出,优化方案改善了原标体的航行中的偏转特性,对比各优化方案,方案1最适合搭载航行。
4 结 论
针对柱形浮标型线优化提出三种优化方案,优化浮标的外部型线,对浮标的水动力学性能产生很大影响。本文利用CFD数值仿真技术,开展相关计算,对不同方案的水动力学特性进行分析获得如下结论:
1)由于原标体结构的特殊性,其首部和尾部结构处产生明显的绕流,形成高压区,在结构后边,形成低压区,符合绕流流场的特性。
2)三种优化针对原标体明显绕流区进行流线型过渡,形式各有不同,通过计算发现,方案1全包裹形式,压力分布最为均匀,无明显的涡量分布,其他两种方案均为局部修改型线,压力分布及涡量分布在局部结构为值出现不均匀性。
3)对比原标体与三种优化方案的阻力及偏转特性,发现,优化方案降低了阻力及偏转力矩等。方案1的阻力降低了84%,偏转力比原标体减小47%,偏转力矩减小57%,对比几种方案,方案1降低最多。
综合压力场、涡量场、速度场分析,配合阻力及偏转特性计算结果,验证了优化方案减阻、改善压力分布的有效性,以全包裹优化的方案1效果最为明显,为后续开展水平搭载运输的自持式剖面漂流浮标优化提供了数据支持。

