基于模糊层次分析法的实验室安全评估

马庚华 郑长江 王天童

摘 要：针对传统实验室安全评价方法准确性差、缺乏统一的评价体系等不足，本文提出了一种基于模糊层次分析法的实验室安全管理评价新方法。通过收集河海大学港口海岸与近海工程学院某实验室的安全数据，采用模糊层次分析法对影响实验室安全的各因素及其权重进行分析，结果表明该实验室存在学生实验操作的专业水平不足、实验室事故防控能力薄弱等问题，并给出相关建议。仿真结果表明，所建立的方法满足合理性和可行性，且模型操作简单，对确保实验室使用者的人身和财产安全具有良好的應用价值。

关键词：安全风险;实验室安全;模糊数学;层次分析法

中图分类号：F224，G482

文献标志码：A

近年来，随着我国越来越重视高等教育的发展，高校实验室的软、硬件设施建设也得到了极大的发展[1]。然而，日益沉重的任务教学和频繁进行的科学研究，再加之实验室相对落后的管理系统，使得实验室在超负荷运行时，出现了因实验室管理不善而造成的重大事故[2]。然而，传统的实验室安全评估采用记录和人工检查的方法对实验室进行监控和管理。由于实验室设备和设备操作的复杂性，以及实验室相关的测试操作方法有很多种，存在各种相关风险[3]。因此，评价的准确性有较大的局限性，只能定性地粗略评价实验室系统的安全性，而不能定量地评价危险程度[4]。

针对以往研究的不足，本文首先采用层次分析法确定评价指标的权重，进而利用模糊矩阵进行计算。通过建立模糊系统，较好地利用了经验知识对信息进行了处理，最终得到了实验室安全管理的结果，并提出相关建议。使得实验室管理人员可以及时发现实验室的违法操作和隐藏故障，提高工作效率，确保实验室使用者的人身和财产安全。

1 研究方法

1.1 安全检查表分析法

本文提出了一种基于模糊数学的安全检查表分析评价方法。安全评价分为三个步骤：按照安全检查表进行标准评分，安全等级划分，提出改进建议。安全检查清单包括实验室用户及人员配备、使用人员的基本要求、规章制度、文件和记录管理、安全信息的收集和交流、登记和变更管理、重大事故的评估和控制、应急相应机制、事故处理[5]。在这些方面列出详细的评价项目和相应的得分，并由相应的专家对评价项目进行打分。该评分机制结合了基于安全检查表数据分析、单项评分和模糊数学的逐项分配方法，进而可以得到实验室的总成绩。根据打分范围，将实验室安全等级分为安全、相对安全、一般安全、不太安全、不安全五个等级[6]。整改建议主要针对不合格实验室，列出实验室使用中违反规定的方面，并提供相应的建议[7]。

1.2 模糊层次分析模型

实验室安全问题是一个模糊的概念，其影响因素很多。因此，有必要使用模糊层次分析（fuzzy analytic hierarchy process，FAHP）算法。将分析对象进行分解，其中所包含的元素被分解为目标层、准则层和因素层。从定量的角度，列举各个影响因素和评价水平，确定各指标的权重。模糊综合评价方法主要包括以下几个步骤[8]。

（1）确定评价集，即一组由专家进行评价的指标及对其进行的描述。评价集的定义为

u={u1，u2，…un}，其中n为待评价的第n个指标的集合，即影响实验室安全的影响因素个数。

（2） 通过定义评估因素来创建观察矩阵V={v1，v2，…vm}，u中的每个方案都是由V中的每个评估因素来度量的。通过专家打分，分别确定准则层和因素层对应的指标得分。专家评分与经过了汇总、计算和规范化的权重相结合。从而，可以得到基于准则层第i个指标的模糊关系矩阵R。

（3） 权重赋值模糊向量a的确定：a={a1，a2，…am}，共有n个因素影响实验室安全，其中m表示权重的个数。

（4） 评价本身由u和V组成，进而形成了评价模糊矩阵R：

Ri=r11r12…r1nr21r22…r2n…………rm1rm2…rmn。（1）

其中，rmn表示第n个指标中第m项的评价因素的数值。

（5）利用模糊算法和公式，将指标权重与因素层的模糊关系矩阵相结合，可得到准则层第i个指标的综合得分向量ui，其中为b赋予权重后的得分。

ui=（ai1，ai2，…，aim）·

r11r12…r1nr21r22…r2n…………rm1rm2…rmn=（bi1，bi2，…，bnm）。

（2）

（6）依次对各因素层的得分向量进行排序，得到目标层的关系矩阵。

R=b11b12…b1nb21b22…b2n…………bm1bm2…bmn。

（3）

多级模糊综合评价将准则层各指标权重的得分矩阵与各因素层的得分向量相结合，利用模糊算子进行模糊综合评价，其中t对应的是评价结果的个数。

u=（a1，a2，…，am）·

b11b12…b1tb21b22…b2t…………bm1bm2…bmt=（b1，b2，…bt）。

（4）

对评价集各层的临界值进行划分，以及评价集对应的分割阈值向量为α=（a1，a2，…，at），从而目标层的综合得分可以表示为：

g=（b1，b2，…，bt）·（a1，a2，…，at）T。（5）

在多级模糊综合评价中，为了体现评价的完整性，还需要分别计算准则层和因素层中各指标的综合得分。其中j为因素层第j个因素。

gi=（bi1，bi2，…，bit）·（a1，a2，…，at）T。（6）

gij=（rij1，rij2，…，rijt）·（a1，a2，…，at）T。（7）

2 计算及结果分析

2.1 模糊综合层次分析法在实验室安全管理评价中的应用

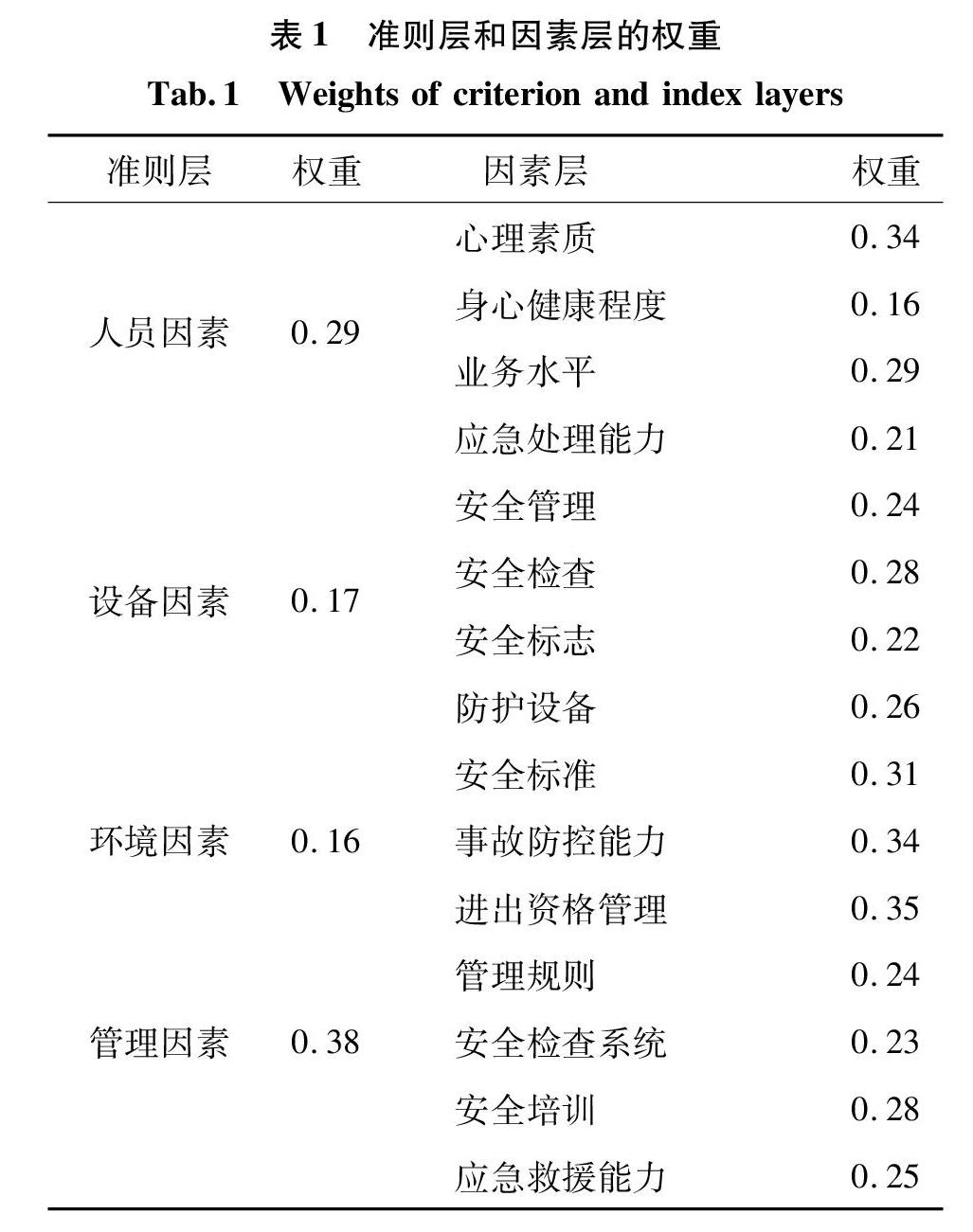
以河海大学港口海岸与近海工程学院某实验室为例，邀请了15位具有丰富实验室安全管理经验的专家，组成安全评价小组，根据工作经验对各项指标进行评分。采用层次分析法和专家问卷法确定实验室安全评价指标的权重[9]。首先将安全评估需要考虑的影响因素分解为目标层、准则层和因素层。然后将下一层的因素与上一层的因素进行比较，构造判断矩阵[10]。通过计算判斷矩阵，对层次进行了单排序和层次分级。通过相关的分析和归一化处理，得到相应的指标权重和模糊关系矩阵，如表1所示，然后利用模糊算子进行多层次的综合评价，得到实验室安全运行管理的综合评价分析[11]。

根据15位专家现场打分，得到准则层的4个因素：人员、设备、环境、管理因素。四个标准水平指标的权重分别为0.29、0.17、0.16和0.38。同时得到因素层的15个指标并赋值，进而可以计算4个准则层指标对应的模糊关系矩阵。

使用模糊综合评分法，4，3，2，1和0，即将临界值向量α=（4，3，2，1，0）分配到{V1，V2，V3，V4，V5}。分别对应于确定实验室安全程度，即{安全，相对安全，一般安全，不太安全，不安全}[12]。

各因素集中程度的评价可通过专家讨论进行评价。具体方法是任意确定一个因子，进行单因子评价，将所有单因子评价结合起来，得到单因子评价矩阵R。例如，55%的人认为安全，15%的人认为相对安全，22%的人认为一般安全，8%的人认为

不太安全。评价集为{0.55，0.15，0.22，0.08，0}[13]。同理，可以得到其他三个评价集的数据。身心健康评价集为{0.65，0.32，0.03，0，0}。业务能力评价集为{0.33，0.36，0.31，0，0}，应急处理能力评价集为{0.58，0.35，0.03，0.04，0}。然后将每个单因素评价集的隶属度划分为若干行，可以形成评价矩阵[14]。

R1=

0.550.150.220.080

0.650.320.0300

0.310.320.3700

0.580.350.030.040;

R2=

0.540.340.060.060

0.730.120.130.020

0.620.340.04000.540.350.1100

;

R3=0.440.530.0700

0.230.440.260.0700.360.470.060.110;

R4=0.630.170.190.0100.440.440.13000.620.320.06000.430.400.150.020;

通过公式（4），可以得到了实验室人员等级u1、实验设备等级u2、实验环境等级u3、实验管理等级u4的综合得分向量。

u1=a1·R1=（0.34，0.16，0.29，0.21）·

0.550.150.220.0800.650.320.03000.310.320.37000.580.350.030.040

=（0.502 7，0.268 5，0.193 2，0.035 6，0）;

u2=a2·R2=（0.24，0.28，0.22，0.26）·

0.540.340.060.0600.730.120.130.0200.620.340.04000.540.350.1100

=（0.610 8，0.281 0，0.088 2，0.02，0）;

u3=a3·R3=（0.31，0.34，0.35）·

0.440.530.07000.230.440.260.070

0.360.470.060.110

=（0.340 6，0.478 4，0.131 1，0.062 3，0）;

u4=a4·R4=（0.24，0.23，0.28，0.25）·

0.630.170.190.010

0.440.440.13000.620.320.0600

0.430.400.150.020

=（0.533 5，0.329 3，0.129 8，0.007 4，0）;

根据因素层的得分向量，得到评价层的综合得分向量为：

u=a·R=（0.29，0.17，0.16，0.38）·

0.502 70.268 50.193 20.035 60

0.610 80.281 00.088 20.020

0.340 60.478 40.131 10.062 30

0.533 50.329 30.129 80.007 40

=（0.506 8，0.327 3，0.141 3，0.026 5，0）。

使用模糊综合评分法，4，3，2，1和0，即将临界值向量α=（4，3，2，1，0）分配到V={V1，V2，V3，V4，V5}。分别对应属于u1，u2，u3，u4和u的实验室安全程度，即{安全，相对安全，一般安全，不太安全，不安全}，进而，目标层的综合得分可以表示为：

g=（0.506 8，0.327 3，0.141 3，0.026 5，0）·（4，3，2，1，0）T=3.32。

然后再分别计算各准则层的指标综合得分：

g1=（0.502 7，0.268 5，0.193 2，0.035 6，0）·（4，3，2，1，0）T=3.24;

g2=（0.610 8，0.281 0，0.088 2，0.02，0）·（4，3，2，1，0）T=3.48;

g3=（0.340 6，0.478 4，0.131 1，0.062 3，0）·（4，3，2，1，0）T=3.12;

g4=（0.533 5，0.329 3，0.129 8，0.007 4，0）·（4，3，2，1，0）T=3.39。

根据安全检查表提供的实验室各目标层、准则层、因素层的得分，可以得出结论，即该实验室的综合评分为3.32分。也就是说，实验室的评分在[安全，相对安全]的范围内，说明实验室的整体运行水平处于相对安全的水平[15]。准则层各指标得分也在[安全，相对安全]的范围内，如表2所示。为了发现该实验室存在的安全隐患，就需要对各个因素层面的影响因素进行详细分析。通过对各个因素层面的得分进行综合分析，发现学生的专业技能和实验室的事件控制能力不足，需要进行整改。同时提出整改建议如下：实验室管理人员和学生应该掌握专业的方法，提高管理员的基本要求，安全使用设备，进行全面、彻底的整改安全相关的所有方面，如风险评估和控制的主要危害，故障处理和隐患整改，清除隐患。

2.2 一致性检测

通过对判断矩阵的一致性进行检验，可以验证评价指标的权重分配是否合理。如果一致性检验不满足要求，则需要对判断矩阵进行调整，直到满足一致性要求[8]。

（1）计算判断矩阵的最大特征根λmax。

（2）检测β=λmax-n（n-1）I，其中I为判断矩阵的平均随机一致性的指标，β为矩阵的相容性指标，当β<0.1时，说明模糊互补判断矩阵满足一致性。

对于1—9阶的判断矩阵，I值如表3所示。通过计算，β<0.01，由于其相容性指标均小于0.1，由此可以说明所进行的权重分配是合理的[8]。

3 结论

采用多级模糊综合评价方法对实验室安全管理进行了综合评价分析，与传统的安全评价方法相比，评价结果更加可靠、直观、准确。案例计算结果显示：

（1）河海大学港口海岸与近海工程学院实验室综合得分为3.32分，表明实验室整体运行水平处于相对安全的水平。

（2）综合分析各指标水平的得分可知，该实验室在学生做实验的业务水平和实验室防控事故能力方面，处于一般安全至相对安全阶段，说明学生做实验的专业能力和实验室防控事故能力方面较为薄弱，因此应该针对性的进行整改和纠正。

（3）针对进入实验室学生的实验水平较为薄弱这一问题，学院应该增设相关的实验室教学及在线模拟等相关课程，强化学生对实验设备，相关材料，实验流程的了解程度。针对实验室防控事故能力薄弱这一问题，学院可以定期检查实验设备，及时替换老化设备，安排专人监督管理。进一步增加该实验室的安全水平。

参考文献：

[1]

金菊良， 魏一鸣， 丁晶. 基于改进层次分析法的模糊综合评价模型[J]. 水利学报， 2004（3）： 65-70.

[2] 杨巍， 程慧高， 云霞. 工程实验室安全风险评估与控制模型研究[J]. 工业安全与环保， 2019， 45（12）： 66-69， 84.

[3] 王扬. 基于大数据的实验室安全风险评估[J]. 现代电子技术， 2018， 41（8）： 113-115， 120.

[4] 钟珊， 张燕. 基于风险分级管控的高校实验室安全管理体系构建[J]. 武汉理工大学学报（信息与管理工程版）， 2019， 41（4）： 364-369.

[5] 刘婷婷， 倪敏， 袁砚， 等. 基于风险评估的环境类实验室安全体系的建设[J]. 实验技术与管理， 2018， 35（11）： 259-262.

[6] OLEWSKI T，SNAKARD M.Challenges in applying process safety management at university laboratories [J].Journal of Loss Prevention in the Process Industries，2017，49（6）： 209-214.

[7] LEE C，ROBERT P.Elements of experiment safety in the laboratory [J].Journal of Chemical Health & Safety，2019，26（4）： 20-25.

[8] PENG T，LI C，ZHOU X B.Application of machine learning to laboratory safety management assessment [J].Safety Science，2019，120（7）： 263-267.

[9] 吕子明， 丁坚平， 褚学伟， 等. 基于模糊层次分析的灰色关联法在地下水水质评价中的应用[J]. 贵州大学学报（自然科学版）， 2019， 36（1）： 118-124.

[10]陈珊珊.佛山科技学院实验室管理研究[D]. 武汉： 华中科技大学，2019.

[11]骆晶晶.高校实验室安全教育培训管理系统建立[D]. 武汉： 武漢科技大学， 2018.

[12]刘晶晶， 张严. 基于RBWM的高校化学实验室安全管理评价体系[J]. 数学的实践与认识， 2020， 50（7）： 277-285.

[13]李浩， 周万怀， 周森鑫， 等. 地方财经类高校实验室综合评价方法探究[J]. 实验室研究与探索， 2020， 39（1）： 279-283.

[14]吳卫， 刘宝勇， 戴亮， 等. 西部地区地方高校实验室安全工作的实践与思考[J]. 实验技术与管理， 2020， 37（4）： 9-11， 15.

[15]邓雪， 李家铭， 曾浩健， 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识， 2012， 42（7）： 93-100.

（责任编辑：于慧梅）

Fuzzy Analytic Hierarchy Process-based

Laboratory Safety Assessment

MA Genghua*1， ZHENG Changjiang2， WANG Tiantong2

（1.College of Harbour， Coastal and Offshore Engineering， Hohai University， Nanjing 210098， China;

2.College of Civil and Transportation Engineering，Hohai University，Nanjing 210098，China）

Abstract：

A new method of laboratory safety management evaluation based on fuzzy analytic hierarchy process is proposed to solve the problems such as the low accuracy of traditional laboratory safety evaluation methods and the lack of a unified evaluation system. By collecting laboratory safety data from College of Harbour， Coastal and Offshore Engineering， Hohai University， using fuzzy analytic hierarchy process， the various influence factors of laboratory safety and their weights were analyzed， and the results show that the laboratory students experimental operation of professional level is of deficiency， laboratory accident prevention and control ability is weak， and related suggestions are given. The simulation results show that the established method is reasonable and feasible， and the model is simple to operate， which is of good application value to ensure the personal and property safety of laboratory users.

Key words：

security risks; laboratory safety; fuzzy mathematics; analytic hierarchy process