横向力作用下摩天轮主轴应力分析及强度校核

摘 要：主轴作为摩天轮最重要的零部件之一，几乎承载着整台设备的全部重量，其设计的安全性和合理性对摩天轮的安全运转和使用寿命都有着直接影响。因此，对摩天轮主轴强度校核尤为重要。在详细分析摩天轮主轴受力的基础上，给出了主轴弯曲正应力和弯曲切应力的计算公式，根据工程力学方法和计算机有限元分析软件对摩天轮主轴进行分析和验算。通过两种方法对比，计算结果误差约1%，并依据GB 8408—2018《大型游乐设施安全规范》对分析结果进行安全性评价，确保主轴的设计满足安全要求，为大型游乐设施主轴的设计生产提供了理论依据，具有一定的工程实用意义。

关键词：机械强度;摩天轮主轴;弯曲正应力;弯曲切应力;疲劳强度;安全系数

中图分类号：TS952.8

文献标志码：A

轴是组成机器的主要零件之一，一切作回转运动的传动零件（例如齿轮、蜗轮等）都必须安装在轴上才能进行运动及动力的传递[1]。摩天轮是一种大型转轮状的游乐设备，主轴作为设备的重要组成部分，是连接大盘和支架的重要部件，几乎承载着大盘的全部重量，是摩天轮最重要的零部件之一[2]。在实际工作过程中，主轴承担了大盘传递过来的各种负载的作用，并将各种负载传递给支架。主轴需要较高的强度、抗冲击性、抗疲劳性能等，其安全性和可靠性是影响设备安全的重要因素，只有使用设计精良、质量可靠、力学性能优越的主轴才能确保摩天轮安全稳定地运行[3]。

国内对主轴强度的研究主要集中在弯曲应力和扭转切应力，对弯曲切应力的研究相对较少，对轴进行强度校核时，往往按照强度理论对弯曲正应力和切应力进行合成，按照合成应力进行校核。以42 m摩天轮主轴为研究对象，利用力学理论公式对主轴进行应力计算和疲劳校核，并应用有限元分析软件ANSYS Workbench建立主轴的模型，进行有限元计算，获得危险截面的应力分布，计算结果表明弯曲正应力和弯曲切应力发生的位置不同，不能简单地按照强度理论进行合成，应分别进行校核计算，并对两种方法计算结果进行分析对比，其计算方法为游乐设施主轴的计算分析提供了一个更为准确的分析思路，具有一定的工程实用意义[4]。

1 设备简介

摩天轮的设备总高度为42 m（不包括避雷针），大盘外悬挂24个透明吊厢，每个吊厢可乘坐4个人，可同时供96人观光，大盘的直径为37 m，总质量为55 t[5]。用电动机通过减速机减速，把高转速低扭矩转为高扭矩低转速的机械动力，通过轮胎等中间机构传到轮盘上，使其低速转动。摩天轮转一周大约需要11 min。摩天轮结构示意图如图1所示。

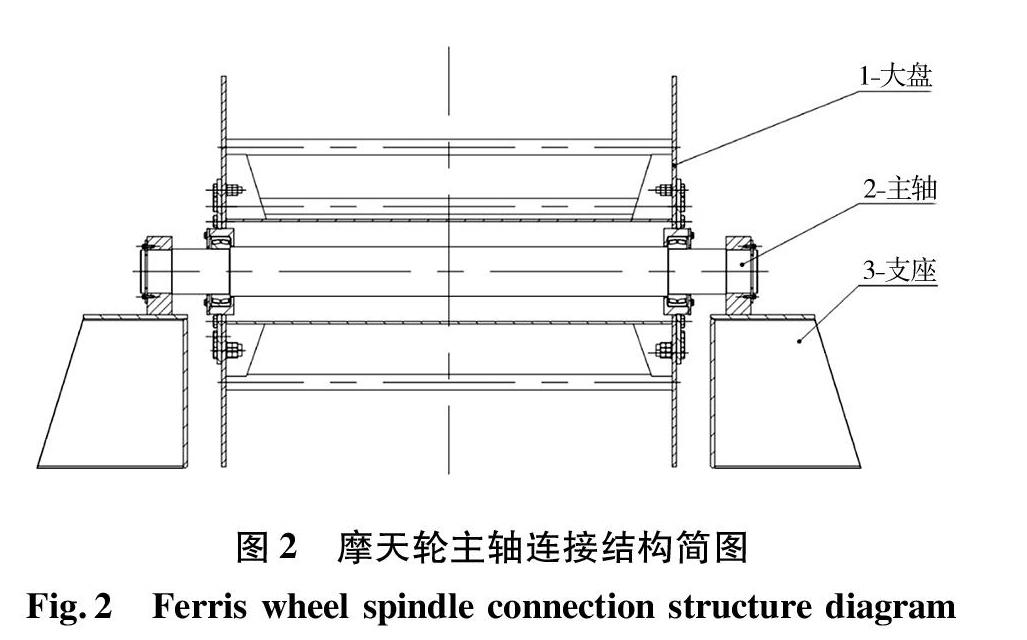
摩天轮主轴是一个大型锻件，是一个起承上启下作用的部件，一方面轴的两端通过支座固定在摩天轮支架上，另一方面通过轴承连接整个大盘。摩天轮主轴结构简图如图2所示。

2 主轴应力分析与校核

2.1 正应力和弯曲切应力计算

前期的设计过程中摩天轮主轴的主要结构尺寸、轴上各零件位置及外载荷和支反力的作用位置均已确定。把主轴当做置于简支座上的梁，力的作用点为轴承的位置点，支反力的作用点为支座的支撑点，轴的计算简图如图3（a）所示。

摩天轮主轴通过轴承与大盘联结，接触面上只传递压力，但不传递扭矩，在轴承部位受到竖向载荷作用下，轴横截面上不仅有弯矩，而且有剪力，弯矩产生弯曲正应力，剪力产生弯曲切应力。主轴的剪力图和弯矩图如图3（b）和3（c）所示。在对摩天轮主轴进行强度计算时，必须同时满足正应力强度条件和切应力强度条件[6]。

摩天轮大盘通过主轴上左右两组轴承与主轴相连接，因此轴承部位受到的大盘对主轴的横向力：

F=mg2。（1）

式中：m为满载工况下摩天轮大盘的总质量，kg;g为标准重力加速度，值为9.8 m/s2。

主轴的横截面积：A=πD24。（2）

式中：D为主轴横截面直径，mm。

主轴截面的抗弯截面系数[7]：W=πD332。 （3）

主轴的最大弯矩[7]：Mmax=F（L-l）2。（4）

式中：L为主轴两支点间的距离，mm;l为主轴两轴承间的距离，mm。

主轴截面上最大的弯曲正应力：σmax=MW。（5）

主轴截面上最大的弯曲切应力：τmax=43FA。（6）

受弯主轴横截面上有两种内力：弯矩和剪力。弯矩M在横截面上产生正应力;剪力F在横截面上产生剪应力。对于横向弯曲下的等直梁（轴），轴上最大的正应力发生在弯矩最大的横截面上距中性轴最远的各点处，而轴的最大弯曲切应力发生在剪力最大的横截面的中性轴的各点处。由于最大正应力和最大切应力发生在轴截面的不同部位，因此需对轴的正应力和切应力分别进行校核计算[8]。

主轴的安全系数是指危险截面的设计安全系数。由于危险截面上作用比较大的弯矩和剪力，计算应力比较大，安全系数比较低。由GB 8408—2018《大型游乐设施安全规范》6.2.2条：材料极限应力与其承受的最大应力的比值为安全系数[9]。

轴弯曲正应力的安全系数：n=σbσmax。（7）

式中：σb为材料的极限应力，MPa。

轴弯曲切应力的安全系数[9]：n=σb3τmax。（8）

由GB 8408—2018《大型游樂设施安全规范》表1：重要的轴、销轴的许用安全系数n≥5.0[10]。

2.2 疲劳强度计算

游乐设施在运行过程中，不断受到满载、偏载等作用，设备结构和零部件承受变化载荷，疲劳破坏是轴失效的主要形式。常规疲劳强度设计认为：材料没有初始裂纹，经过一定次数的应力循环后，由于疲劳损伤的累积，形成微裂纹，微裂纹在应力循环下不断扩展，主轴断面面积不断减小，直至发生脆性断裂[11]。因此主轴的疲劳破坏是塑性材料发生的脆性断裂。

疲劳强度计算的实质在于确定变应力情况下轴的安全程度。轴通常采用安全系数法进行校核计算。疲劳强度安全系数校核，是在轴经过初步设计计算和结构设计后，根据轴的实际尺寸，考虑零件的表面质量、应力集中、尺寸影响以及材料的疲劳极限等因素，验算轴的危险截面处的疲劳安全系数[12]，并使其大于或至少等于许用设计安全系数。

摩天轮运行过程中，乘客不断上上下下，此时主轴受到的不单是静态载荷，同时还受到交变载荷的作用。在交变载荷作用下不但要计算主轴的静态强度，还应校核其疲劳安全系数。

轴仅受正应力时的疲劳安全系数[13]：

Sσ= σ-1Kσ βεσ σs+ φσ σm 。（9）

轴仅受切应力时的疲劳安全系数[13]：

Sτ= τ-1Kτ βετ τs+ φτ τm 。（10）

轴同时受到正应力和切应力时的安全系数[13]：S=SσSτS2σ+S2τ。（11）

式中：σ-1，τ-1为正应力和切应力的材料疲劳极限，MPa;Kσ，Kτ为正应力和切应力的有效应力集中系数;β为表面质量系数;εσ，ετ—尺寸影响系数;φσ，φτ为平均应力折算系数;σs，τs为应力幅，MPa;σm，τm为平均应力，MPa。

由GB 8408—2018《大型游乐设施安全规范》表2可知，对于材料较均匀，载荷和应力计算较精确时，在脉动循环应力作用下，轴的许用疲劳安全系数S≥1.73[10]。

2.3 实例计算

满载工况下，摩天轮大盘的总质量为m=55 t（包含乘客），主轴直径D=210 mm，材料为45钢（热处理，抗拉强度σb=580 MPa），轴支座距离L=2 700 mm，轴承之间的距离l=2 200 mm。

由公式（1）可得主轴受到的集中载荷：

F=269.5 kN;

由公式（2）可得主轴的横截面积：

A=34 636 mm2;

由公式（3）可得主轴的抗弯截面系数：

W=9.1×105 mm3;

由公式（4）可得主轴受到的最大弯矩：

Mmax=67 375 Nm;

由公式（5）可得主轴受到的弯曲正应力：

σmax=74.0 MPa;

由公式（6）可得主轴受到的弯曲切应力：

τmax=10.4 MPa;

由公式（7）可得摩天轮主轴弯曲正应力的安全系数：n=7.8;

由公式（8）可得摩天轮主轴弯曲切应力的安全系数：n=32.2。

摩天轮主轴的安全系数大于5.0，表明主轴满足应力强度的要求。若小于安全系数，需对主轴尺寸参数重新进行设计，或选用抗拉强度较高的材料。

摩天轮主轴的材质为45钢，以上参数均可在《机械设计手册》（第二卷）第6篇查询得到：σ-1=320 MPa，τ-1=150 MPa，Kσ=1.5，Kτ=1.39，β=0.9，εσ=0.6，ετ=0.6，φσ=0.34，φτ=0.21。

摩天轮运行过程中处于满载、偏载等交变工况下，主轴始终受到向下的压力作用。保守计算，按照脉动循环进行疲劳校核，应力幅和平均应力等于最大应力的一半。则：

σs=σm=37.0 MPa，τs=τm=5.2 MPa。

将上述数据代入公式（9）、（10）可得：

Sσ=2.8，Sτ=10.4。

将Sσ和Sτ代入公式（11）可得：S=2.7。

由此可知，摩天轮主轴的疲劳安全系数大于许用安全系数，满足疲劳设计的要求。

3 有限元计算

3.1 有限元模型及载荷

有限元法的基本思想是将连续体划分为有限个单元的组合，进行有限元分析首先应建立合理的几何模型，通过对几何模型进行网格划分，生成包含节点和单元的有限元模型[14]。几何模型的合理性关系到能否生成有限元网格和比较好的网格质量。因此，需在不影响分析结果的前提下对几何模型的特征进行简化忽略。

根据分析要求对摩天轮主轴进行适当的几何清理，删除对计算结果影响不大的细小圆角、卡簧槽等，轴的材料为45钢，弹性模量E=2×105 MPa，泊松比υ=0.3，密度ρ=7 800 kg/m3。由2.1节主轴的尺寸参数，主体采用高阶三维10节点实体单元Solid187进行网格划分，采用六面体网格[15]，网格尺寸为20 mm，节点数为113 537个，单元数为26 367个，在ANSYS Workbench中建立的摩天轮主轴有限元模型，如图4（a）所示。

主轴两端安装在支座上，安装部位约束径向位移（cylindrical support），大盘与主轴通过轴承连接，连接部位分别施加竖向向下载荷（force）269.5 kN。载荷与约束如图4（b）所示：

3.2 有限元计算结果

經过有限元分析计算，在竖向载荷作用下，主轴的弯曲正应力（normal stress）如图5（a）所示，最大应力出现在主轴上表面，最大值为75.0 MPa;主轴的弯曲切应力（shear stress）如图5（b）所示，最大应力出现在主轴侧表面，最大值为10.5 MPa。有限元计算结果与理论公式得到的计算结果相符（误差约1%），说明有限元分析方法对摩天轮主轴进行强度计算的快捷性与可靠性，摩天轮主轴满足设计的要求。

由计算结果可知，当轴受到横向力作用并对轴进行强度计算时，弯曲正应力最大值出现在横截面上离中性轴最远处，而最大切应力出现在危险截面的中性轴上，因此对轴的校核必须同时满足正应力的强度条件和切应力强度条件。一般情况下，轴的强度计算由正应力强度条件控制。按正应力强度条件设计的截面常可使切应力远小于许用切应力（本例计算结果切应力安全系数远大于正应力安全系数）。所以一般情况下，总是根据轴截面上的最大正应力来确定轴的设计参数，然后再按切应力强度条件进行校核。

4 结论

以某摩天轮主轴为工程背景，对主轴在横向载荷作用下进行分析计算，计算结果表明：

（1）主轴在横向力作用下，受到弯曲正应力和弯曲切应力的共同作用;

（2）由于最大弯曲正应力和弯曲切应力发生的位置不同，不能按照传统强度理论进行合成计算，应分别按照弯曲正应力和弯曲切应力进行应力和疲劳校核计算;

（3）应用工程计算与有限元相结合的方法，能够更加真实地模拟主轴的受力情况，对主轴的分析更为准确。仿真结果与理论计算结果比较，表明计算结果的可靠性和正确性。

用有限元分析软件ANSYS Workbench进行计算，在合理简化模型、正确加载与约束下，相对于常规设计计算，可以快速和深入地对结构进行分析，提高了计算精度和效率，计算结果形象直观。通过分析可知，该型号摩天轮主轴应力和疲劳满足设计要求，其计算方法和结果可为游乐设施主轴的计算分析提供参考，对于提高工程技术人员的设计能力具有现实意义。

参考文献：

[1] 陈涛，张丽.小型手动压力机的设计[J].现代机械，2017（4）：131-132.

[2] 李纪友，王浩然.摩天轮主轴内部缺陷与案例分析[J].机械，2016（S1）：93-95.

[3] 毛淳誠，林胜洋，曹广启.大型风电机组主轴强度分析[J].机械工程与自动化，2015（5）：82-86.

[4] 赵九峰.游乐设施压杆稳定性计算原理解析[J].机械，2020（6）：32-36.

[5] 赵九峰.基于ANSYS的摩天轮安装模拟分析[J].机械工程与自动化，2019（2）：38-41.

[6] 刘海燕，覃文洁，李欣.柴油机曲轴的多轴高周疲劳寿命估算[J].机械强度，2013（6）：844-849.

[7] 范钦珊.工程力学[M].北京：高等教育出版社，2009.

[8] 李依伦，李敏.直梁弯曲切应力的讨论[J].力学与实践，2016（5）：572-577.

[9] 付恒生，林明，梁朝虎.大型游乐设施设计[M].上海：同济大学出版社，2015.

[10]中国特种设备检测研究院，江苏省特种设备安全监督检验研究院，中山市金马科技娱乐设备股份有限公司，等，GB 8408—2018大型游乐设施安全规范[S].北京：中国标准出版社，2018：32-33.

[11]赵九峰.新版《大型游乐设施安全规范》部分条款分析与解读[J].特种设备安全技术，2020（1）：50-52.

[12]陈启锐.机床主轴的设计方法[J].机械研究与应用，2017（4）：143-144，147.

[13]成大先.机械设计手册[M].北京：化学工业出版社，2016.

[14]金峰方，修君.扩展有限元法及与其它数值方法的联系[J].工程力学，2008（S1）：1-17.

[15]李传闪，梁栋，陈兵奎.塑料蜗杆与钢质斜齿轮啮合特性分析及实验研究[J].机械传动，2017（12）：58-62.

（责任编辑：曾 晶）

Stress Analysis and Strength Check of the Main Shaft

of Ferris Wheel Spindle under Lateral Force

ZHAO Jiufeng*

（Special Equipment Safety Inspection and Research Institute of Henan Province， Zhengzhou 450000， China）

Abstract：

As one of the most important parts， Ferris wheel spindle carries almost all its weight. The safety and rationality of its design have a direct impact on the safe operation and service life of the Ferris wheel， so it is particularly important to check the strength of the spindle. In this paper， the force of Ferris wheel spindle is analyzed in detail， and the calculation formulas of bending normal stress and bending shear stress of the spindle are given. According to the engineering mechanics method and the finite element method， the Ferris wheel spindle is analyzed and checked. The comparison shows that the error of the calculation results is about 1%. According to GB8408—2018 "Large-scale amusement device safety code"， safety evaluation was conducted on the analysis results to ensure the safety of spindle. It provides a theoretical basis for the design and production of the spindle of large amusement facilities， which has certain practical significance in engineering.

Key words：

mechanical strength; Ferris wheel spindle; bending normal stress; bending shear stress; fatigue strength; safety factor