不确定性数学方法的比较研究

秦贞燕+王永丽+于慧慧+周杰

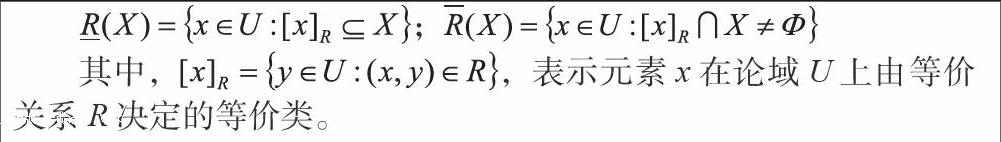
摘要：概率统计，模糊数学，灰色系统，粗糙集和未确知数学是目前存在的五种不确定性数学方法。本文针对不确定性信息及其数学方法的概念进行了阐述和分析，并且比较了五种方法的不同之处，使人们更清晰的认识和区分这五种不确定性数学方法及其应用领域。

关键词：概率统计；模糊数学；灰色系统；粗糙集；未确知数学；不确定性信息

中图分类号：TP273 文献识别码：A 文章编号：1001-828X（2016）009-000-03

Abstract： Probability statistics， fuzzy mathematics， gray system， rough sets and unascertained mathematics are five existing uncertainty mathematical methods at present. This text described and analyzed the concept and the mathematical methods of uncertain information，and compared the difference of five methods， to make people understand and distinguish these five uncertainty mathematical methods clearly.Probability statistics.

Keywords： Probability statistics； fuzzy mathematics； gray system； rough sets； uncertain information；

一、引言

经典数学的研究对象局限在确定性对象，因此人们又称之为确定性数学。在信息多变的.时代，不确定现象无处不在，其存在形式各式各样。人类在不断认识世界和改造世界的过程中发现经典数学不再是解决问题的有效途径。面对大量得不确定现象，如何从数学上定量的描述这些不确定现象，并研究不确定现象数量规律及优化问题一直是人们追求的课题研究。在研究过程中，人们发现了信息的不确定性是多种多样的，并将多样的不确定性信息进行分类表述，就出现了信息的随机性、模糊性、灰色性、粗糙性和未确知性，相关的概率统计、模糊数学、灰色系统、粗糙集和未确知数学学科也被专家一一提出，做了深入研究，并且取得良好的理论和应用成果[1，2，3]。

我们把研究自然社会中存在的不确定现象的数学理论和方法统称为不确定数学。因此，概率统计、模糊数学、灰色系统、粗糙集和未确知数学学科都可以包含在不确定数学的范畴之中[4]。这五种学科是当前研究不确定性问题的不同的数学方法，这些学科的发展也就是反映了不确定性数学的发展。

二、不确定性信息

不确定性是指客观事物在发展与联系的过程中，存在无序的，或然的，未知的，近似的属性。任何一个复杂的系统都存在不确定性因素，不确定性因素的产生不仅仅涉及主观因素，还会涉及很多客观因素，而且是两者交互影响。由于信息的产生及其传播的过程条件不同，不确定信息的表现会有不同的特征。根据这些不确定信息的表现特征，人们将已认识到的不确定性信息主要分为如下五种。

1.随机信息

在随机现象中，事件结果是确定的，由于偶然因素干扰，使得几种确定结果呈或然性出现。即在某次试验中事件在相同的情况下却有不同的结果，这种试验称为随机试验。由随机试验得到的信息称为随机信息。如市场价格波动、彩票中奖情况等[5]。由随机信息引起的不确定性称为随机不确定。

2.模糊信息

因为事物的复杂性，事物的自身概念外延不明确，即事物特征界限不明确，其概念不能准确的被描述和评定。事物从一方概念到另一方概念存在过渡的过程，它提供的很难说清边界的的信息称为模糊信息[6]，如稳定、不稳定、健康、不健康等。由模糊信息引起的不确定性称为模糊不确定。

3.灰色信息

在事物发展过程中，由于人们接收信息系统的能力有限，使得人们只能获取事物发展的部分信息，而不能获得全部的确切信息。即部分信息已知，部分信息未知[7]。这种外延明确内涵不明确的信息我们将之称为灰色信息。如玉米的产量、金融市场中的股票市场等。由灰色信息引起的不确定称为灰色不确定。

4.粗糙信息

由于不确定性，导致事物的不可辨性。事物的集合是明确，但其中所包含的元素是不明确的，这种信息被称为粗糙信息。它与模糊信息的区别在于，模糊信息的集合边界不确定。如人的外貌、人的品质。由粗糙信息引起的不确定性称为粗糙不确定。

5.未确知信息

未确知信息是指因为条件的限制，在进行决策时，无法确知的信息[8]。这些信息既无随机性，也无模糊性，它是由于决策者所掌握的信息不充足，不精确。以至不足以确定事物的真实状态和数量关系。这种未确知信息可以带来主观认识上的不确定性。如地震的震源、一座已建成的建筑物的重量等。由未确知信息引起的不确定性称为未确知不确定。

三、不确定性数学方法

1.概率统计

1657年，荷兰著名数学家惠更斯就对随机性进行研究，随后前苏联数学家柯尔莫哥洛夫提出并建立的概率论。概率统计是以随机现象为基础。概率论是根据大量相同随机现象的规律，对在随机现象某一结果出现的的可能性给出客观的科学的判断，并且进行数量方面的描述[9]。

要研究一个随机现象，首先要研究明白它服从的概率分布，但是在现实当中，有些随机现象所服从的分布是什么概型可能完全不知道，有的根据现象自身的特点和已经发生出现的结果，我们可以推测出其服从的概型，却不能确定其分布函数中所含的参数值。例如，某天某公路段所行驶每辆车的速度服从什么分布是完全不能知道的，某一商业部收购N件产品，每件产品不是合格就是不合格，显然产品的是否合格得情况是服从二项分布，但分布中的参数P（不合格品率）却是不知道的。为了要掌握上述车辆速度的分布、不合格品率，我们必须对这一公路上所行使的车辆速度及工业产品是否合格进行观察和试验。类似这种统计处理寻求参数值就是概率统计的应用之处。在数理统计的过程中，我们总需从待研究的全体对象中随机或有目的地抽取一部分进行观测或试验以取得所需信息，从而对研究对象作出推断。每个推断都伴随一定的概率用以表明推断的可靠程度。像这种伴有一定概率的推断称为统计推断[9]。数理统计中假设检验、参数估计、方差分析和回归分析等思想也都达到成熟状态并在气象预测、保险工作、抽奖活动、质量判断、游戏活动等方面得到了很好的应用。

2.模糊数学

1965年，扎德教授论文“模糊集合”的发表标志着模糊数学的诞生[10]。模糊集合的提出是模糊信息客观存在的必然反映。面对模糊问题，如判断生态环境是否文明，“生态文明”没有一个确切衡量标准，怎样才算是生态文明是无法说清楚的，也就不能用普通实数集合论里仅取0或1两个值的特征函数来刻画。为了解决类似问题中含有连续过渡的共性，扎德将普通集合论里的特征函数的取值范围由{0，1}推广到闭区间[0，1]，用一个实数去度量它，这个实数值我们称之为是隶属度[6]。

定义1[6]设在论域U上给定了一个映射

则称A为U上的模糊集，A（u）称为A的隶属度函数（或称为u对A的隶属度）。

隶属度函数在模糊数学理论应用中占有至关重要的地位，是将模糊性运用数学方法来解决的关键媒介。隶属度函数的确定，是一个比较复杂的问题，在许多实际情况下，通常根据经验或统计规律来决定。

模糊数学有着相当丰富的研究内容，到目前为止，经典数学中的很多理论分支学科也进行模糊化，成为模糊数学学科的组成部分。如模糊关系、模糊矩阵、模糊变换、模糊拓扑空间、模糊图论、模糊概率统计、模糊线性规划、模糊逻辑、模糊变量、模糊博奕等。广泛的模糊分支使模糊数学在生活中的很多方面得到了良好的应用。

3.灰色系统

1982年，邓聚龙教授创立的灰色系统理论，是针对研究少数据、贫信息不确定性问题的新方法[7]。灰色系统的研究方法主要是通过对现有的“部分”已知信息的开发，挖掘有效的信息，实现对系统运行行为、演化规律的正确描述和有效监控。灰色系统理论重点研究的是具有“外延明确，内涵不明确”特点的对象。比如到2050年，中国将人口控制在15亿到16亿之间，这个“15亿到16亿之间”就是一个灰概念，其外延很清楚，但进一步问15亿到16亿之间的哪个具体值，则不清楚[11]。

灰色系统理论认为，尽管客观事物的表面现象复杂，数据无序，它们总会蕴含着自身的特征规律，关键是如何选择合适有效的方法去利用和挖掘信息。对数据构造不同的算子成是灰色系统处理信息的重要手段。

定义2 [11] 设初始数据序列为：X （0）（k）=（x（0）（1）， x（0）（2）， …， x（0）（n）），D为序列算子

X （0）D=（x（0）（1）d， x（0）（2）d， …， x（0）（n）d ）

其中，。则称D为X （0）的一次累加生成算子。X （0）D为X （0）的一次累加生成序列。

定义3[11] 设初始数据序列为：X （0）（k）=（x（0）（1）， x（0）（2）， …， x（0）（n）），D为序列算子

X （0）D=（x（0）（1）d， x（0）（2）d， …， x（0）（n）d ）

其中：x（0）（k）d = x（0）（k）-x（0）（k-1）；k=2，，3，…n

则称D为X （0）的一次累减生成算子，X （0）D为X （0）的一次累减生成序列。

累加生成和累减生成是在灰色系统中使灰色信息变白化的一种方法，累加生成的数据可以用来描述灰色数据积累过程的发展势态，使不具有明显规律的原始数据中蕴藏的累积特性充分显现出来。累减生成也是在获取增量信息时常用的一种手段，累减生成可以还原累加生成。累减生成与累加生成是一对互逆的序列算子，它们是构建GM（1，1）模型的理论基础。

灰色系统在经典数学理论的基础上生成了很多彼此相关的理论，包括灰数运算、灰色代数系统、灰色方程、灰色矩阵等。此外，灰色系统在实际应用方面也构建了许多经典模型，如用于系统诊断、分析的系统灰色关联分析模型；用于解决系统要素和对象分类问题的灰色聚类评估模型；用于方案评估和选择的灰靶决策和多目标加权灰靶决策模型，以及灰色规划、灰色投入产出、灰色博弈、灰色控制等[7]。其中灰色系统理论在农业科学、经济管理、环境与安全科学、天文和地球科学方面应用较为突出和广泛。

4.粗糙集

在灰色系统成立的同时，1982年，Pawlak教授针对G.Frege的边界线区域思想提出粗糙集理论[12]。与其他不确定方法不同，粗糙集的基本思想是用已有的知识库中的知识和信息，通过等价关系来近似表示不确定的未知目标。上近似算子和下近似算子是粗糙集理论的基础，是粗糙集依靠等价关系判定分类的手段。

定义4[13] 设U为一论域，R是U上的等价关系，对于任意XU，X基于等价关系R的下近似R（X ）与上近似R（X ）分别定义如下：

目前，粗糙集理论在现实中的应用研究主要集中在属性约简、规则获取、基于粗糙集的计算智能算法等方面。粗糙集的知识约简理论的发展为数据挖掘提供了一些有效的新方法。例如、数据分析法、基于信息熵的属性约简算法、动态约简算法、增量式算法、可辨识矩阵算法等[12]。此外，粗糙集结合信息论、概念格、群体智能算法技术等也都有了显著的的研究成果[14，15]。目前粗糙集理论的应用领域涉及决策分析系统、数据挖掘、模糊粗糙集控制、粗糙神经网，以及医疗诊断、专家系统等诸多方面。

5.未确知数学

1990年，我国学者王光远教授提出了未确知信息，从而创立了未确知数学理论。未确知数学主要研究、表达和处理未确知信息的一种理论与方法。若想将未确知的事情变成已知，主观概率和主观隶属度函数是未知数学的重要依据。所谓主观概率[16]，就是人们对某个未确知事件的各种可能情况为真几率的主观估计。因为有时候研究的是已发生的事件，因而没有随机性，又因为是一次性事件，因而主观概率不存在任何统计的含义。主观隶属度[16]的产生是由于采用解决模糊性信息的手段来处理未确知的信息。例如，通过测量分析后，估计某一条河水的重量为3000吨左右。这个回答是用一个模糊量来估计大量液体的重量这个确定性的量。它纯粹是回答者对该具体量的一种主观上的粗略估计，因而称为主观隶属度分布。

未确知数学也根据原数学的领域进行了推广，建立了“未确知集合”、“未确知顺序”、“未确知函数”、“未确知极限”等相关的数学内容。

四、五种不确定数学方法的比较

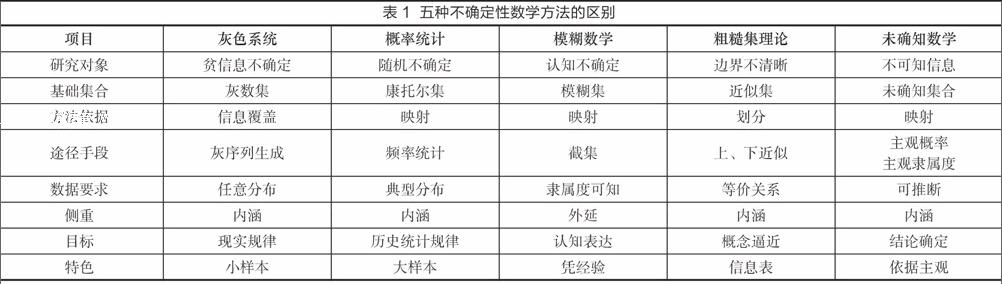
概率统计、模糊数学、灰色系统、粗糙集和未确知数学是当前存在的解决不确定问题的五种数学方法，他们彼此之间存有相似之处却又彼此不同。而其研究对象都具有某种不确定性，这是他们的共同点。正是研究对象在不确定性上的区别，派生出五种各具特色的不确定性学科。综上所述，我们可以把五种常用不确定性数学方法的区别归纳如表1所示。

五、小结

本文主要探讨了五种不确定性数学方法的特点，并对其区别及其应用领域进行了总结。由于信息的复杂化，在很多情况下，多种不确定性信息相互参杂，因此出现了多种复合型不确定性数学方法。不确定数学方法应用领域非常广泛，几乎涉及到学科领域的各个角落，如经济学、逻辑学、管理学、气象学、医学、情报学、系统论、控制论等方面，尤其在人工智能、工业生产、综合评价、模式识别、聚类分析、层次分析等理论中应用显著。概率统计和模糊数学理论提出较早，很多专家对这两个不确定性数学方法内容研究深刻，所以该些方法的理论应用都达到了相对成熟的状态。而灰色系统、粗糙集和未确知数学仅仅经过了二、三十年的研究，很多理论方法正在发展和完善过程中。

参考文献：

[1]Wen-xiu Li，Dong-liang Qi，Shao-feng Zheng Fuzzy mathematics model and its numerical method of stability analysis on rock slope of opencast metal mine.Applied Mathematical Modelling， 2014.

[2]靖洪文，吴俊浩，马波杨，圣奇.基于模糊灰色系统的深部巷道围岩变形预测模型及应用[J].煤炭学报，2012.

[3]马文萍，黄媛媛，李豪，李晓婷，焦李成.基于粗糙集与差分免疫模糊聚类算法的图像分割[J].软件学报，2014.

[4]李群..不确定性数学方法研究及其在经济管理中的应用[D].大连理工大学，2002，1～2.

[5]王清印，刘志勇.不确定性信息的概念、类别及其数学表述[J].运筹与管理，2001.

[6]周浩亮.模糊数学基本理论及其应用[J].建井技术，1994（4、5）.

[7]刘思峰.灰色系统理论的产生与发展[J].南京航空航天大学学报，2004.

[8]王光远.未确知信息及其数学处理[J].哈尔滨建筑工程学院学报，1990.

[9]魏宗舒，黄先开.概率论与数理统计教程[M].北京：高等教育出版社，2008.

[10]石瑞民.模糊数学思想及与经典数学思想的辩证关系[J].中国人民公安大学学报，2003

[11]刘思峰，郭天榜，党耀国.灰色系统理论及其应用（第七版）[M].北京：科学出版社，2014.i～ii.

[12]王国胤，姚一豫，于洪.粗糙集理论与应用研究综述[J].计算机学报，2009.

[13]张文修，仇国芳.基于粗糙集的不确定决策[M].北京：清华大学出版社，2006.

[14]Li H R， Zhang W X， Wang H. Classification and reduction of attributes in concept lattices//Proceedings of the 2006 IEEE International Conference on Granular Computing （GrC.06）. Georgia State University， Atlanta， USA， 2006：142-147.

[15]Liang J Y， Shi Z Z， Li D Y， Wireman M J. The information entropy， rough entropy and knowledge granulation in incomplete information systems. International Journal of General Systems， 2006， 34（1）： 641-654.

[16]梁红.未确知数学在地铁工程施工安全评价中的应用研究[D].北京：中国地质大学，2010.28～19.

作者简介：秦贞燕（1990–），女，山东济宁，汉族，山东科技大学在读研究生，研究方向：数据挖掘。王永丽（1977–），女，山东烟台，汉族，山东科技大学副教授，主要从事最优化理论与算法、支持向量机的研究。于慧慧（1991–），女，山东菏泽，汉族，山东科技大学在读研究生，研究方向：分布式优化。周 杰（1990–），男，山东济宁，汉族，淄博矿助理工程师、技术员，工作方向：工程测绘。