三星系统运动规律初探——由一道竞赛题引发的思考

赵少云，陈绍锋

（南宁市第二中学 广西 南宁 530029）

1 引言

万有引力定律在双星和三星系统中的应用，是高考和物理竞赛中常见的考点。这部分内容涉及到天体力学的基础知识和基本研究方法，如果引导高中物理特长生研究三星系统规律，既可以提高他们的分析推理能力，还可以提升他们对天体力学的兴趣，为国家储备更多的理论研究人才，是一件非常有意义的事情。

有这么一道物理竞赛题，题目是：有的三星系统由两个质量为m的小星体和质量为M的大星体组成，两个小星体在同一圆形轨道上运行，轨道半径为r。引力常量为G，试说明三个星体的相对位置并求出小星体的运行周期。1该题目的一种解答是：

如图1，大星体在轨道中心，两个小星体保持在轨道的同一条直径上绕大星体运行。小星体运动所需的向心力由大星体和另一个小星体对它的万有引力F1和F2提供。根据万有引力定律、牛顿第二定律和圆周运动公式有：

图1 两小星体在同一直径绕位于圆心的大星体运行

笔者认为，这是一道考查中学生解题能力的好题，而且还可以进一步思考以下问题：

（1）若M不是静止的而是运动的，三者还能保持一定的距离吗？

（2）如果三星的质量不相等，结论是否有变化？

2 孤立的三星系统的模型

2.1 稳定的三星系统应满足的条件

天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。双星系统在银河系中很普遍。这些双星大多远离其他星体，而且其中每个星体的线度都远小于两星体间的距离。我们暂且把仅在万有引力作用而保持相对位置不变的系统称为稳定系统。系统内的两颗恒星在对方的万有引力作用下，绕它们连线上某点做匀速圆周运动，而该点其实就是双星系统的质心。因为，两个星体只有绕着它们的质心做匀速圆周运动，保持到该点的距离不变，才可以使双星的质心在系统内的相对位置不变，这样的双星系统才是稳定的系统。

同样，假若双星系统中再增加一颗星体就可组成三星系统，只要满足其中每个星体的线度都远小于任意两星体间的距离，且都远离其他星体，该系统就是一个孤立的系统。稳定的三星系统应该满足这样的条件：系统内的任何一个星体在其他两星的万有引力作用下绕着系统的质心做匀速圆周运动；保持三星的质心在系统内的相对位置不变。

2.2 由两个质量相等的小星体和一个大星体组成的三星系统模型

本文开始提到的那道竞赛题答案中所提供的三星模型确实是稳定三星系统的模型之一。在这个模型中，两个小星体的质量相同，所以大星体所在位置即是三星系统的质心位置，两小星体到质心的距离相同，故做匀速圆周运动的半径也相同，他们可在同一个圆形轨道上运行。但是，很明显，这不是三星系统的唯一模型，三个星体只要围绕着它们的质心旋转即可维持系统的稳定性，所以三星可以不在同一条直线上，而应该可以分别位于三角形的三个顶点上。因题中要求两个小星体在同一个圆形轨道上运转，即它们的轨道半径相同，这就要求两个小星体到质心的距离相同，这至少要求这个三角形是一个等腰三角形，大星体位于该等腰三角形顶角的顶点上。如图2 所示。

图2 假设三星组成任意底角的等腰三角形

我们似乎可以得出这样的结论：这样的三星系统可以组成任意底角的等腰三角形，底角的大小由M和m的比例关系决定。我们不妨假设这个结论是正确的，在此前提之下寻找底角和三星质量大小的关系。

如图3 所示，设三个星体分别位于等腰三角形ABD的三个顶点上（M位于A点，两m分别位于B点和D点上）。因两小星体的质量相等，所以两个m的质心在BD边的中点E处，故三星的质心C应位于BD边的垂直平分线AE上，如图。设两个小星体间的万有引力为F1，小星体和大星体间的万有引力为F2，小星体所受的万有引力的合力为Fm；三角形ABD的两个底角为θ，Fm与底边的夹角为α；底边BD的长为2a，两小星体的轨道半径为r，大星体的轨道半径为R，即BC=DC=r，AC=R。

图3 质心C 位于两小星体连线的垂直平分线上

由万有引力定律得：

Fm的方向为：

把(1)(2)代入(3)整理得：

因为C为三星的质心，由质心公式可得：

所以得：

又由于CE=AE-AC=a·tanθ-R，所以再由质心公式可得：

从(7)式中可解出：

把(8)式代入(6)式可把R消去：

而Fm是小星体做匀速圆周运动所需的向心力，必然指向质心C，所以∠CBD=α，即式⑷=⑼，则：，整理得：，所以，即θ=600。

以上证明过程中，M、m和a均是任意的，所以这个结果表明，由两个质量相等的小星体和一个大星体组成的三星系统所围的三角形是一个等边三角形，而不是底角任意的等腰三角形。

2.3 任意质量关系的三星系统模型

2.3.1 模型一

我们可以进一步推想，以上这个特殊的结论是否是由于系统内有两个星体的质量相等才造成的？如果是这样，那么当三星的质量都不同时，是否会组成一个任意的三角形呢？我们也不妨假设这个猜想是正确的，在此前提之下来寻找这个任意三角形的三个角与三星的质量间的关系。

如图4 所示，设三个星体分别位于任意三角形ABD的三个顶点上（m1位于A点，m2位于B点，m3位于D点）；设∠ABD=θ，∠ADB=φ。过A点作BD边的垂线交BD于O点，以O点为原点，BD方向为x方向，OA方向为y方向建立直角坐标系xOy。设AO=a，则A点的坐标为（0，a）；因为BO=a/tanθ，DO=a/tanφ，所以B点和D点的坐标分别为（-a/tanθ，0）和（a/tanφ，0）。

图4 假设三星质量都不同时组成一个任意的三角形

设系统的质心为C，其坐标为（xC，yC），则由质心的公式可得：

设CB连线与x轴正向夹角为α，CD连线与x轴负向夹角为β，则由几何关系得：

把(10)(11)式和B、D两点坐标代入(12)式整理可得：

由万有引力定律可得m1和m3对m2的引力分别为：。因为m2绕质心C做匀速圆周运动所需的向心力由F12和F32的合力来提供，所以F12和F32的合力F2一定沿着BC连线指向C，即F2的方向与x轴正向的夹角也为α，则：。整理得：

同样，也可以根据⒀式和m3所受的万有引力导出与⒃式对称的式子：

对比(16)和(17)式可知θ=φ，并由此解出：cosθ=1/2，所以θ=φ=600。

因为以上推导所用三星质量和a均是任意的，所以可以得出一个普遍的规律：即任意质量关系的三星系统所围的三角形也是等边三角形，而不会是任意三角形。

2.3.2 模型二

当然，三星也可以不围成一个等边三角形，还有另一种简单的模型，就是三星排成一条直线，中间一颗星刚好在旁边两星的质心上，两星围绕着中间星体做匀速圆周运动，如图5 所示。

图5 三星排成一条直线

3 孤立的三星系统的运动规律

3.1 模型一

3.1.1 运转周期

通过以上推导，可以推断，在模型一中，三星绕它们的质心旋转的周期应由三星的质量关系和它们所围的等边三角形的边长来决定，我们同样也可以通过万有引力定律和几何关系推出周期公式。

设三星的质量分别为m1、m2和m3，它们分别位于边长为a的等边三角形ABD的三个顶点上，如图6。用E表示m2和m3的质心，则由质心的定义可得：，

图6 任意质量的三星分别位于等边三角形的三个顶点

由余弦定理得：AE2=AB2+BE2-2AB·BEcos600=。

用C表示m1、m2和m3的质心，则C在AE上，设m1、m2和m3绕C做匀速圆周运动的轨道半径分别为r1、r2和r3，则有：

同理可得：

根据万有引力定律得m2和m3对m1的引力分别为：

F21和F31的合力F1的作用线一定过质心C，其大小为：，把(21)式代入上式可得：

同理，m2和m3所受引力的合力F2和F3的作用线也一定过质心C，大小分别为：

设三星绕质心做匀速圆周运动的角速度为ω，由牛顿第二定律可得：F1=m1ω2r1

把(18)和(22)式代入上式解出ω：

则周期为：

可见，三星的运转周期由三星的质量之和与边长的立方的比值决定。

3.1.2 线速度关系

由(18)(19)(20)式和公式v=rω可得三星的线速度之比为：

3.2 模型二

3.2.1 运转周期

如图5 所示，设m1和m2之间的距离为L，m3位于质心C上，m1和m2的轨道半径分别为r1和r2，它们绕m3旋转的角速度为ω。由万有引力定律可得m1和m3对m2的引力分别为：

由牛顿第二定律得：F2=F12+F32==m2ω2r2

上式经整理得：

由质心公式可得：

把(30)式代入(29)式，解出角速度得：

则周期为：

3.2.2 线速度关系

再由(30)式和公式v=ωr可得m1和m2的线速度之比为：v1:v2=r1:r2=m2:m1

4 三星系统的特例

4.1 特例一

本文开头所提到的那道竞赛题，所涉及到的是三星系统中较特殊的一种，即其中两星的质量相等。由以上讨论可知，质量相等的两星轨道半径一定相同，也一定会在同一个圆形轨道上绕系统的质心运行。这样的三星系统模型应该有两种，一种就是原题中答案所提供的模型，即本文所提到的三星模型二；另一种应该是三星围成一个等边三角形的模型一，如图7 所示。

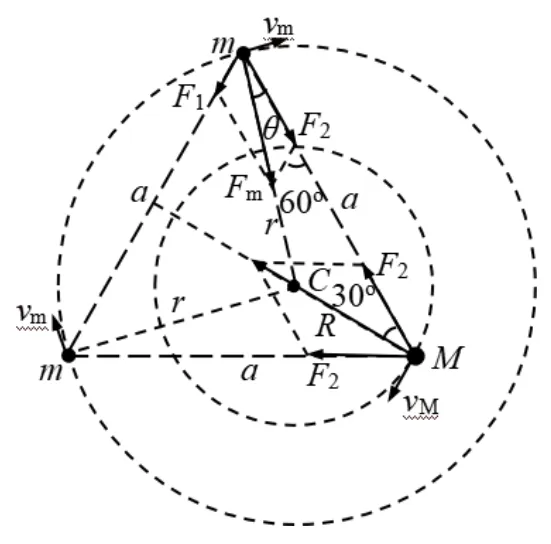
图7 三星围成一个等边三角形

根据上面第(32)式，把m1=m2=m，m3=M，L=2r代入该式，就可以得到题中的答案：。

而把m1=m2=m，m3=M，r1=r2=r代入⒅式可得：a=，再把该式代入(26)式，即可得该题的另一个答案：。

4.2 特例二

假若三星的质量均相同，即m1=m2=m3=m，则当三星排成一条直线时，其周期公式为：，而当三星围成一个等边三角形时，三星围绕该等边三角形的中心，即三星的质心旋转，如图8 所示，其周期公式为：。

图8 三星围成一个等边三角形且绕三角形的中心旋转