基于单元评价的试卷命题设计策略——以人教版五年级上册“多边形的面积”单元为例

（福州市鼓楼第一中心小学，福建福州 350001）

所谓单元试卷，是指单元课程结束后，教师通过命题考试的方式，评价学生综合应用单元知识解决数学问题能力的试卷，是激励学生学习、改进教师教学以及提高教学质量的重要手段。在单元试卷设计中，教师多是充当命题的“搬运工”，存在试题理念守旧、内容枯燥、形式单一等问题，导致单元试卷的价值降低，培育和发展学生综合能力的功能受限。“多边形的面积”这个单元的评价目标是在理解掌握平行四边形、三角形、梯形面积计算方法的基础上，通过练习促进学生对公式的灵活应用，加强图形之间的沟通和转化能力。通过图形的转化或分割，计算组合图形面积或估算不规则图形的面积。下面以人教版五年级上册“多边形的面积”这个单元为例谈谈如何利用命题，实现其单元评价目标。

一、基于知识的“基础性”，体现试题层次

理解掌握多边形面积计算方法是“多边形面积”单元学习的知识基础。以往教师们为了“夯实基础”，在单元试卷命题时，会把着力点放在“计算图形的面积”上。显然，这种命题仅停留于学生对公式的简单运用上，其效果属于“机械记忆”，而未达到公式的“灵活应用”。这样的命题势必使学生沦为“刷题利器”，学生怨声载道，收效甚微。在考查学生单元基础知识时，教师可将命题设计植根于单元架构之中，以多边形面积计算为“架”，活用公式为“魂”，以实现“到位”而不“越位”。

【例1】如图1 所示，在一组平行线间画以下四个图形，且每个图形的底边都相等。你能根据图形面积公式，判断下列图形中面积最大的是（）。

图1

这道命题设计，教师把握了“没有基础是不行的，只有基础是不够的”的原则。创造性地将命题中的数据删去，目的是考查学生灵活运用公式，实现图形间的沟通和转化。学生解决问题，可通过一般方法，尝试借助代数思想计算解答；亦可将平行线间平面图形的面积大小，从底乘高的层面转为底边长短的比较，使思维水平从知识的机械应用提升到本质探索。这样的命题，既能使优生吃饱，也能使学困生吃好，做到基础与提升两不误。

二、基于试题的“生活化”，激发学生解题兴趣

弗赖登塔尔认为：“数学教育应该源于现实，用于现实。”小学生的思维还处于形象思维向抽象思维过渡的阶段。命卷时，若能将多边形面积的计算植入对话、数据、游戏、热点新闻等生活载体中，则更能凸显数学解决问题的本质，更能让学生感受数学的理性思考，更能展现数学生动活泼、富有挑战性的一面，激发学生的解题兴趣，一定程度上培养学生丰富的想象力、应用意识和创新能力。［1］

【例2】同学们，少年先锋队队旗是我们生活中常见的组合图形。图2 标注了队旗的相关数据。聪聪通过分割转化的方法，列出计算队旗面积的算式：80×60-60×20÷2。请你根据算式，判断下列选项中，属于聪聪的分割方法的是（）。

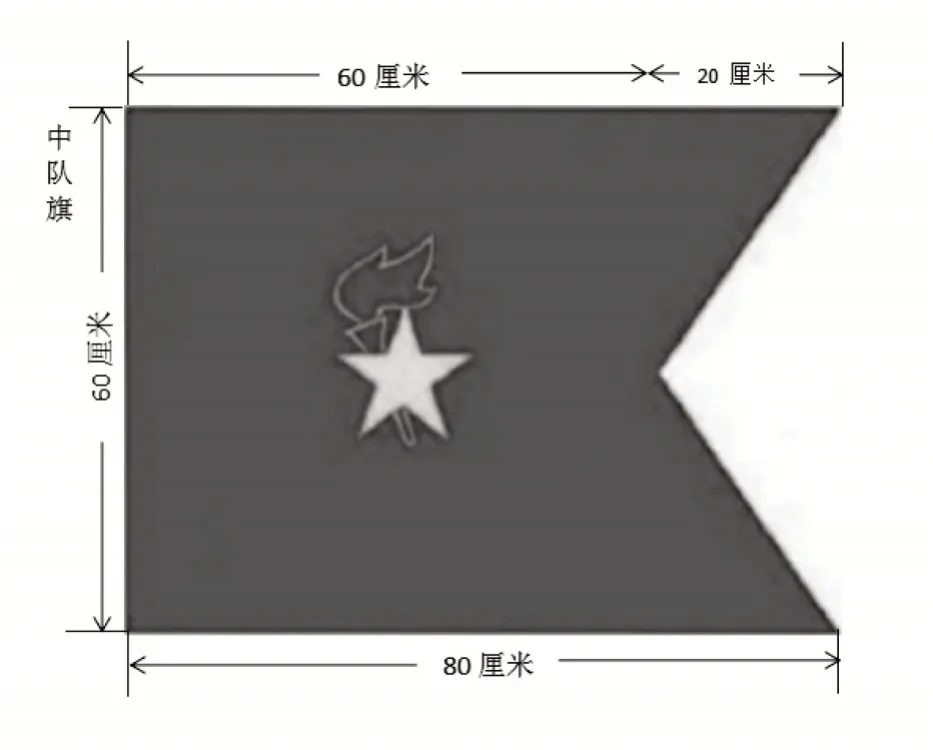
图2

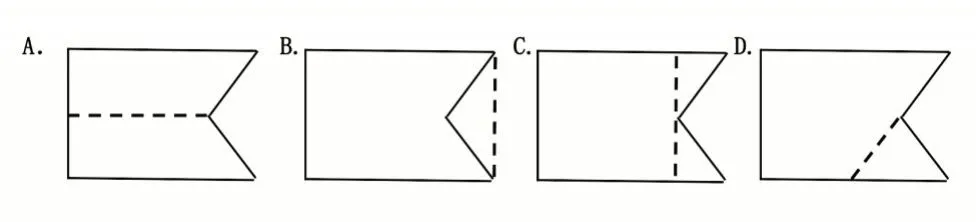
本题改变以往组合图形面积的命题以“面积计算为主”的评价方式。命题以队旗为解决问题的素材，让学生经历对算式观察、分析、动手操作等数学思考，通过“以数解形”的尝试，推导出图形分割的方法，发展学生的逆向思维和推理能力。学生在情境的烘托下，对试题倍感亲切，不再感觉试卷中只有冰冷的数字或是枯燥的公式，激发其解决问题的主动性，感悟数学试卷中的“生活味”。

三、基于学习的“过程性”，实现知识内化

《义务教育数学课程标准（2011 年版）》明确指出，“要重视过程，处理好过程与结果的关系”，并提倡“在练习设计时，积极探索可以考查学生学习过程的习题，了解学生的学习过程”。由此可见，新课程理念下的评价导向，已经发生根本性变化。它不再是应试教育背景下，仅关注学生结果的对错，而是探索素质教育下，学生知识的形成、发展的“过程”以及内化的“结果”。［2］因此，多边形面积单元的评价目标，应更关注学生对图形面积的沟通与转化，能够优化求解面积的方法，而非面积计算结果的成败与否。若一味地强调结果、轻视过程，会让学生陷入“知其然，而不知其所以然”的学习窘境。如何在单元试卷中，体现“过程性”，落实多边形面积单元教学的“过程性”目标呢？可通过公式的推导与应用，让学生经历基础知识的形成过程和问题解决的思维过程。

（一）立足公式推导，丰富基础知识形成的过程

公式推导是“多边形的面积”单元教学内容的重点。教师在教学设计时，往往会给予学生充分的时间，经历、探索多边形面积公式的推导过程，通过图形间的转化比较，理清图形间“变与不变”的关系，进而帮助学生熟练掌握面积公式。对于推导公式的考查，传统的命题设计可能更侧重公式推导的机械识记，而忽视对本质的探索。基于此，可尝试设计这样的命题：

【例3】如图3 所示，把平行四边形沿着高剪下后，拼成一个长方形，请根据信息作答。

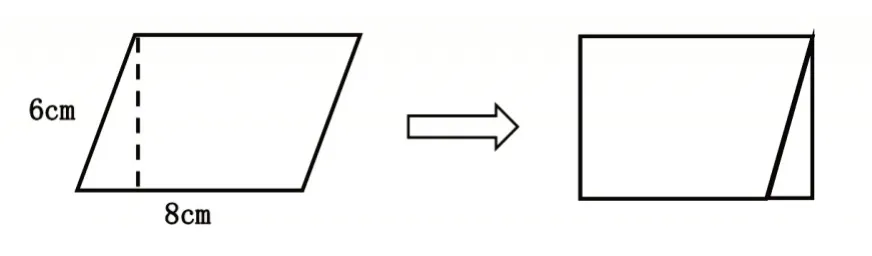
图3

（1）拼成后的图形的周长的取值范围，可能是（）cm。

A.大于28B.在32 和48 之间

C.大于24，小于28 D.无法确定

（2）拼成后的图形的面积是（）平方厘米。

A.大于48B.小于48

C.等于48D.无法确定

命题展示了平行四边形通过剪拼转化成长方形的公式推导过程。通过问题导向，引导学生关注到图形周长与面积间“变与不变”的关系。虽然本题最后还是离不开周长和面积的计算，但是重心却转移到对“剪拼前后，图形周长变了，面积不变”的本质意义的探索过程。这样的命题设计，丰富了学生体验基础知识的形成过程。

（二）立足公式应用，暴露问题解决的思维过程

传统的单元试卷，在“公式应用”的评价目标上，大多数教师侧重于结果对错的评价；命题形式的呈现，则侧重于单一的计算或填空，忽略学生在应用公式解决问题时思维过程的反馈，无法展示学生思维的现有水平与独特方式。在试卷命题时，可以尝试多层次、多形式结合，凸显学生解决问题的过程和方法，暴露学生思维的路径或痕迹，使命题起到检测学生思维过程的作用。可设计这样有层次的练习：

【例4】（1）下列图形不能直接求出面积的是（）。

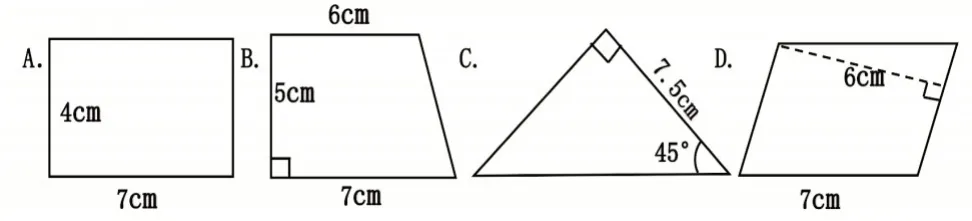
图4

（2）若想求出这个图形的面积，还需要测量哪些数据？请你量一量，算一算。

试题设计时，教师注重对学生“多边形面积”公式应用的考查。题目设置了两道相关联的小问题，使层次更加突出，思维逐步提升。学生先要通过辨析和判断，找到不能直接求取面积的图形。通过动手测量获取有效信息，进而解决问题。学生在完成试题的过程中，充分经历解决问题的过程，展示了问题解决的策略和思路，提升解决问题的能力。

四、基于学科的“融合性”，聚焦综合能力

《义务教育数学课程标准（2011 年版）》指出：“要将数学知识与其他学科知识有机融合，从其他学科中挖掘可以利用的资源作为命题背景，通过解决数学问题，实现渗透和解决其他学科中的问题。”因此，教师在单元命题设计时，可尝试将数学知识与其他学科的学习内容进行融合，通过多种知识、方法与能力的综合运用，增强学科知识间探索性、思想性、趣味性，树立学生的文化自信与认同感。

【例5】阅读与解答

同学们，听说过勾股定理吗？我国古代的一部数学著作《周髀算经》，记载了公元前11 世纪，周朝数学家商高与周公的一段对话。商高曰：“……故折矩，以为勾广三，股修四，径隅五。”意思是：直角三角形的两条直角边分别为3（勾）和4（股）时，径隅（弦）则为5。以后人们就将此发现称为勾股定理。西方国家最早提出并证明此定理的为公元前6 世纪古希腊的毕达哥拉斯学派，毕达哥拉斯用演绎法证明了直角三角形斜边平方等于两直角边平方之和。这个结论比我国晚了近500 年，可见我国古人的智慧。

请你根据这则数学故事中的信息，完成下列各题。

（1）直角三角形的两条短边分别长6cm 和8cm，它的第三条边长（）cm。

A.6B.8

C.10；D.大于2，小于14

（2）请你根据第（1）小题的选择，求出这个三角形的面积，并求出斜边上的高。

数学阅读是顺利、有效地进行数学学习活动的重要基础，是对文字、数学符号、术语、公式、图表等的感知和认读。本例题设计，旨在让学生通过数学阅读，提取有效的数学信息，并将数学信息与数学知识相结合，以解决数学问题。学生对于此种题型并不陌生，他们可以用语文学科中短文阅读的一些学习方法来解决此类问题。不同的是，语文学科注重文字表达，而数学学科则体现数学逻辑和数学符号。此类命题设计，既有“浓浓的数学味”，又有“厚厚的爱国情”，在提升学生的数学素养同时，增强学生对民族文化的认同感和自信心。［3］

总之，单元试卷中的命题设计的质量影响对学习评价的效果。教师只有把准单元的评价目标，用心去设计试卷，才发挥其导向作用，全面落实育人目标。