压入尺寸效应对AZ31镁合金应变率敏感性的影响

王 在， 邱 吉， 冯嘉仕， 金 涛， 树学峰*

(1.太原理工大学机械与运载工程学院， 太原 030024； 2，中国人民武装警察部队山西省总队医院， 太原 030024)

镁及镁合金广泛应用在航空航天、汽车制造和精密仪器制造等领域[1]。作为晶体结构为密排六方(HCP)的金属材料，镁合金具有相对复杂的变形失效机理[2]。镁合金由于其密度小(1.78～1.91 g/cm3),比强度、比刚度高，尺寸稳定性和导热率高，机械加工性能好，而且其产品易回收利用，有望成为21世纪重要的商用轻质结构材料，是一种目前极具竞争力的轻量化材料[3-4]。

镁合金板材在实际工程中应用很广泛，由于板材厚度方向的尺寸小，传统的拉伸压缩、扭转等力学性能测试技术无法适用于薄板结构。对于其力学性能的表征可以引入特殊的手段。纳米压入法通过对材料的微小区域进行局部测试，从而获得材料的力学性能参数，是解决这一类问题的有效手段。

Almasri等[5]对面心立方的金属材料进行纳米压入实验，并对压痕尺寸效应进行了分析。Voyiadjis等[6]分别使用单一刚度法和连续刚度法对Al、Cu等金属进行硬度测试，发现压入深度对压入硬度有着显著的影响。Somekawa等[7]通过纳米压痕实验对Mg-Al、Mg-Zn镁合金的力学性能进行研究，发现镁合金的纳米硬度和应变速率相关，而合金的成分及初态组织等因素对硬度的影响较小。Pham[8]通过纳米压入的方法对钢的力学性能进行研究，结合拉伸实验结果，得到材料的弹塑性参数；Basu[9]等人研究了尺寸相关的塑性响应，结果表明：局部组织对小尺度塑性响应有明显影响。Zhao等[10]发现，在纳米压入实验中，金属合金的硬度和弹性模量都表现出明显的应变率正相关性。

目前大量文献通过压痕测试手段，得到并分析了镁合金一些基础的力学性能。由于压痕试验中尺寸效应的存在，需要通过纳米压痕对镁合金的力学性能进行深入的研究。采用轧制镁合金板材，使用纳米压入方法对其沿轧制方向(RD)切割试样进行实验，以了解材料的力学性能。采用连续刚度法对AZ31的压痕尺寸效应和应变率敏感性进行了深入研究，详细讨论了压入尺寸效应对该材料应变率敏感指数的影响[11]。

1 材料与实验流程

图1 AZ31试样Fig.1 The specimen of AZ31

2 结果和讨论

p(t)=AeCt

(1)

式(1)中：A为加载常数；C为应变率；t为时间。图2为应变率为0.01 S-1的荷载-时间曲线，通过曲线拟合可以得到A值，应变率为0.01、0.05、0.1、 0.15、0.2 S-1时，A值分别为0.075、0.071、0.069、0.05、0.038。可以看出，随着应变率的增大，A值逐渐减小。

图3为在5种不同应变率下的荷载-压入深度曲线。可以发现，在同一压入深度下，随着应变率的增大，荷载呈增大趋势，表现出明显的应变率相关性。在深度达到700 nm，应变率敏感性表现得更明显。

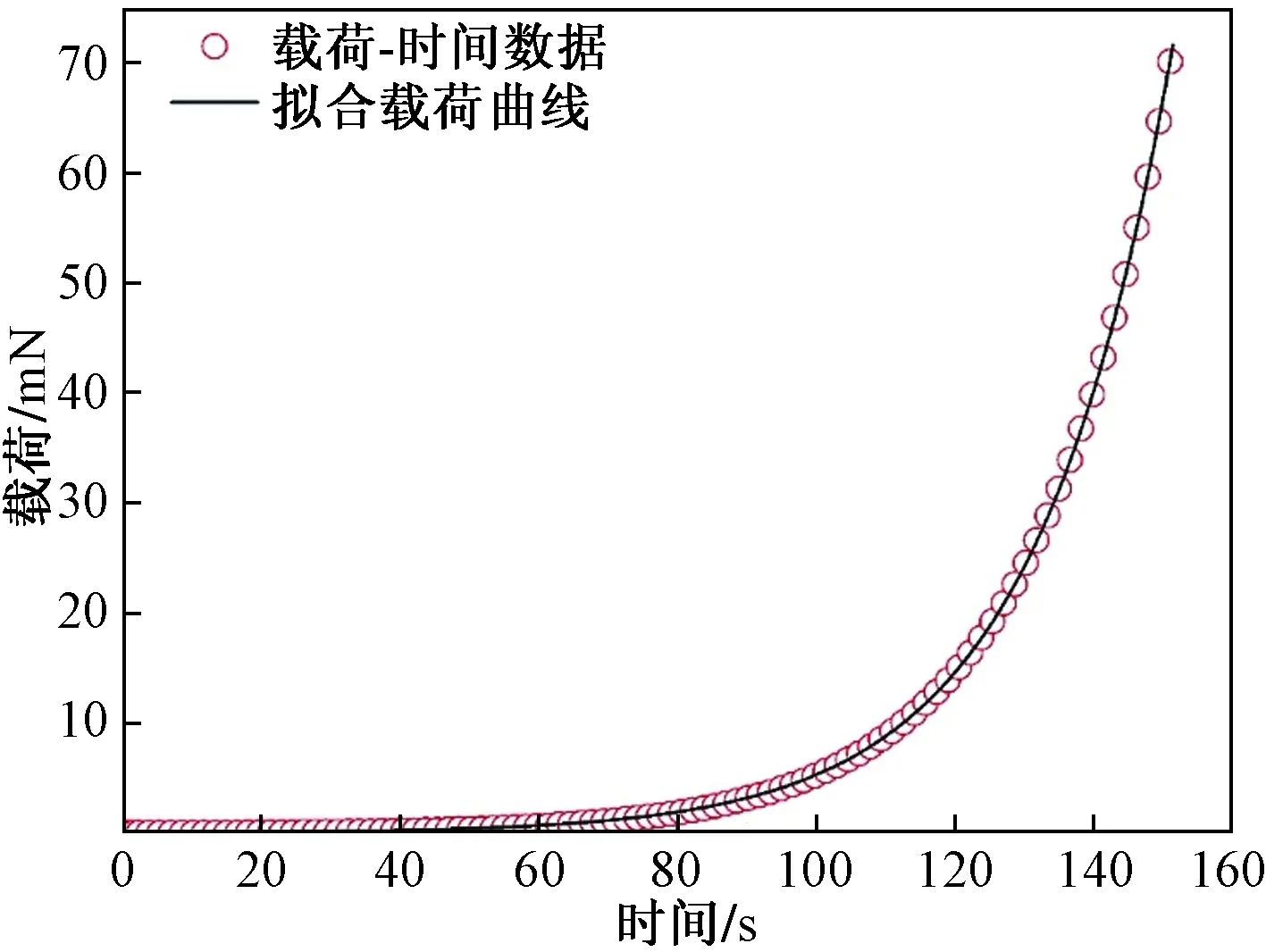
图2 纳米压入荷载-时间曲线Fig.2 Load-time curve for the nanoindentation tests

图3 5种应变率下的荷载-深度曲线Fig.3 Load-depth curves at five strain rate

基于CSM模型，接触刚度的表达式为[14]

(2)

式(2)中：S为接触刚度；Famp为振幅，hamp为振幅；ω=2πf为角频率，f=45 Hz；m、ks、kf分别为压头质量、垂直方向的弹性常数及刚度常数。

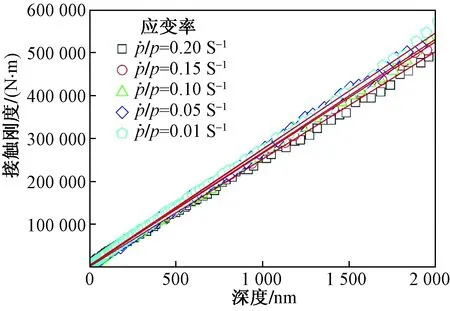
图4 5种应变率下的AZ31接触刚度-深度曲线Fig.5 Contact stiffness-depth for AZ31 under five strain rate values

由图4所示，不同应变率下随着压入深度增大接触刚度呈线性。由此得到接触刚度斜率k，如表1所示。

对于理想的压头，接触面积Ac可表示为[15]

(3)

式(3)中：hc为接触深度，其计算公式为

表1 不同应变率下接触刚度斜率Table 1 Fitting slope of contact stiffness under different strain rate

(4)

式(4)中：p为接触荷载；ε=0.75为Berkovich压头的常数。

折合模量(Er)可表示为[13]

(5)

式(5)中：β=1.034，是Berkovich压头的常数，其折合模量的计算公式为[16]

(6)

式(6)中：v为镁合金泊松比；Ei、vi分别为压头的弹性模量和泊松比，Ei=1 141 GPa、vi=0.07[17]。根据上述条件可以得到轧制镁合金在不同应变率下的弹性模量，如图5所示。显然，不同应变率下的弹性模量值不发生变化，表现出应变率无关。

图5 5种应变率下的弹性模量-深度曲线Fig.5 Elastic modulus-depth curves at five strain rate

硬度(H)计算公式为

(7)

图6 5种应变率下硬度-深度曲线Fig.6 Hardness-depth curves at five strain rate

由式(7)得到5种应变率下压入深度-硬度的关系，如图6所示，随着压入深度增加，硬度值逐渐减小趋于一个恒定值。随着压入应变率的增大，所得到的硬度值变大，但在0.01、0.05、0.015 S-1应变率下的硬度差距较小。因此，对于纳米压入应变率敏感的材料，要综合考虑应变率与尺寸效应对材料力学性能及参数的影响。

通常使用应变率敏感指数(m)来描述材料性能与应变率的相关性,m也可以反映材料的塑性能力，其表达式为[18]

(8)

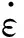
(9)

因此m可以通过两个参数的对数函数关系求得，如图7所示。

图7 不同压入深度下m值Fig.7 The value of m under different ranges of indentation depth

图7为不同应变率下的硬度，选取压深在500～1 500 nm的数据。分别选取500～750、750～1 000、1 000～1 250、1 250～1 500 nm深度的平均硬度。显然，随着压入深度的增加，应变率敏感指数(m)接近常数。对于金属材料的应变率敏感性一般受到位错激活的影响。而位错激活体积v*可以通过式(10)进行预测[19]。

(10)

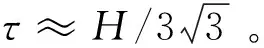
综上所述，需要进一步考虑纳米压入中尺寸效应对于力学性能的影响。采用Nix-Gao提出的硬度模型[20]：

(11)

(12)

图8 不同应变率下的H2-1/h曲线Fig.8 H2-1/h curves at different strain rate

表2 不同应变率下的H0Table 2 H0 at different strain rate

同样，剔除尺寸效应影响的应变率敏感指数(m0)为

(13)

图9 双对数坐标下Fig.9 Double logarithmic plots of ln

3 结论

通过纳米压入的方法研究了压入尺寸效应对AZ31镁合金应变率敏感性的影响。实验发现压痕应变率对AZ31的接触刚度及弹性模量没有影响，而对硬度值的影响较为显著，且呈正相关性。此外，在不同的压痕应变率下，随着压痕深度的增加均表现出明显的压痕尺寸效应。分析了压痕尺寸效应对硬度和应变率敏感性的影响，得到了剔除尺寸效应的硬度(H0)和应变率敏感指数(m0)，进而为AZ31镁合金在实际工程应用中提供理论指导。