飞行器表面沉积静电分布仿真

方庆园， 周江波， 季启政， 冯 娜， 刘卫东

(1.石家庄铁道大学河北省电磁环境效应与信息处理学科重点实验室， 石家庄 050043； 2.北京东方计量研究所， 北京 100086)

飞机在高空中飞行时，会因与空间粒子进行摩擦等因素在飞机表面形成静电积累[1]。随着飞机表面电荷的不断积累，飞机表面的电压不断升高。当飞机表面积累电荷所产生电场高于空气击穿场强时，就会产生静电放电。静电放电所产生的电磁干扰会影响民用和军用飞机的安全运行。

Beach[2]对飞机飞行中表面电荷积累原理进行了研究。Nanevicz[3]研究了喷气式飞机的静电起电原因及放电电流，得到了静电放电电流的一般规律。Ter Haseborg等[4]研究了子弹在空气中高速飞行时的带电情况，在一定范围内预测弹丸上的电荷数量和飞行弹丸周围的电场分布。Grosshans等[5]详细阐述并验证了摩擦带电模型，以预测直升机在尘土飞扬的空中盘旋时的电气化情况，对电荷积累的位置进行详细分析。Lekas[6]提出了飞机在沙尘中飞行所产生的静电电荷量的一种计算方法，并证明了该方法也可用于计算飞机与雨滴、雪花、冰晶等大气颗粒物与飞机相互摩擦所产生的静电电荷量。Revel等[7]提出了在飞机表面布置探测器定位飞机在飞行状态下静电放电部件的方法。Andersen等[8]研究了聚合物材料的静电放电分布，改善了空间环境中的静电放电击穿场的估计。Yadav等[9]介绍了多种航空纳米复合材料在飞机抗静电中的应用及发展。易鸣等[10]研究了固定翼飞机静电分布特性及着陆时静电泄放，用矩量法分别求取了飞机空中飞行和停靠地面时的电荷分布。杨真一等[11]研究了放电刷对飞行器静电放电的抑制作用，得到增加放电刷直径是排放机体电荷最为有效的方法。Hu等[12]对飞机表面的摩擦起电规律进行了理论分析和试验研究，得出了飞机的摩擦带电极性。张靖等[13]研究了某型飞机静电放电刷的静电泄放特性和影响参数。刘浩等[14]研究了某飞行器表面硅基热防护材料静电起电和泄漏特性及影响因素。左曦等[15]通过对飞机充氧阀头系统的两种材料进行试验，验证与分析了多种因素对不同材料接触静电积累的影响，得出了抗静电材料可以有效降低氧气系统中接触静电的产生。

综上可知，中外对飞机静电起电及放电问题均比较重视，并开展了大量研究工作，但针对全尺寸条件下飞机的静电电荷及电场分布规律研究相对较少。为此，通过构建飞行状态下塞斯纳飞机的三维全尺寸模型，研究其表面沉积静电电荷与电场分布规律，以及飞行状态下塞斯纳飞机表面沉积静电电荷与电场分布。首先建立了某型号飞机的1∶1沉积静电仿真模型。然后基于该模型仿真了飞行状态下飞机的电容，将仿真所得飞机电容与经验公式所得飞机电容进行对比验证。最后研究了模型结构、沉积电荷量对飞机表面电荷密度与电场分布的影响。为分析评估飞机沉积静电危害提供参考依据。

1 飞机建模

研究对象为某型号塞斯纳飞机，该飞机机身长度为14.91 m，翼展为16.72 m，高度为4.57 m。在SolidWorks 中建立该飞机的1∶1仿真模型如图1所示，飞机主要由机身、机翼、引擎、驾驶舱、机舱舷窗和放电刷构成。其中放电刷结构一致，由圆柱和锥台构成，圆柱底部半径为0.005 m，长度为0.15 m，锥台底部半径为0.005 m，顶端半径为0.001 m，长度为0.01 m。机舱舷窗边长为0.40 m，厚度为0.02 m。

2 飞行状态下飞机电容计算与仿真

由于飞机的几何形状复杂，因此无法准确通过解析表达式计算其电容，此处采用类比的方法求解飞机电容[16]。根据文献[17]可知，自由空间中金属球体的电容计算公式为

C=4πε0R

(1)

式(1)中：ε0=8.85×10-12F/m，为真空介电常数，F/m；R为金属球半径，m；C为电容，F。

在CST(computer simulation technology)仿真软件的电磁工作室中，球体电容的计算公式为

C=4πε0εr[R1R2/(R2-R1)]

(2)

式(2)中：εr为相对介电常数，在空气中εr=1；R1为内层球体的半径，m；R2为与内层球体同心的外层球体的半径，m。在CST电磁工作室中仿真球体电容，其中，内层球体的半径R1为0.1 m，外层球体的半径R2为1～15 m。

内层球体材料为理想导体(perfect conductor，PEC)，外层球体材料为空气。对内层球体施加1 V电压，图2为利用CST电磁工作室仿真所得球体电容，包括仿真所得电容和式(1)计算所得电容的相对误差。

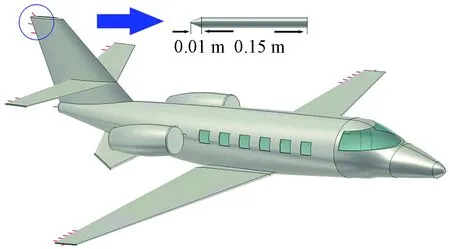
图1 1∶1飞机仿真模型Fig.1 1∶1 aircraft simulation model

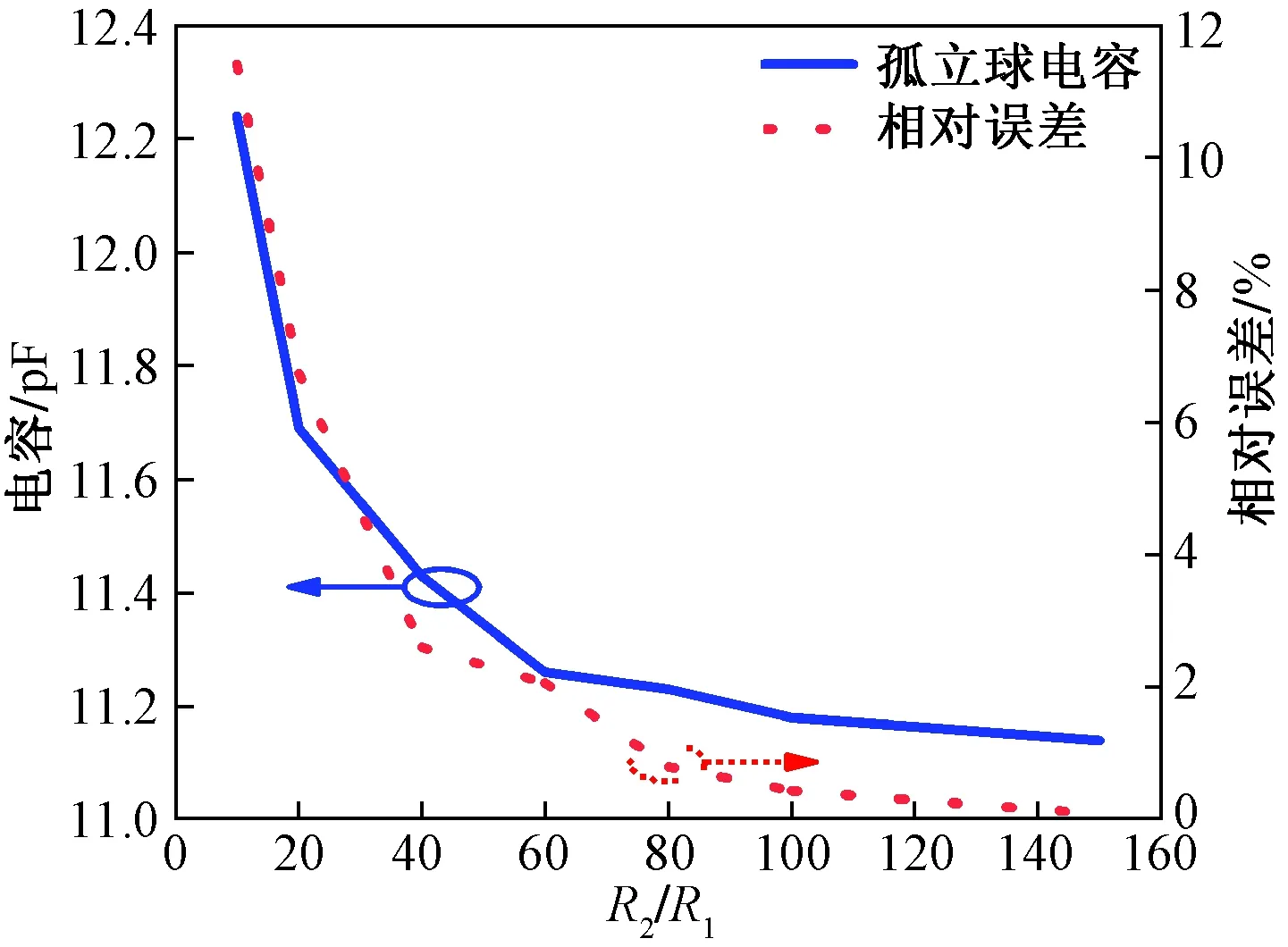
图2 孤立球的电容仿真结果和相对误差Fig.2 Isolated ball capacitance simulation results and relative error

由图2可知，当外层球体半径逐渐增大时，球体电容逐渐下降最终趋于稳定。当外层球体半径为内层球体半径的150倍时，仿真所得电容为11.14 pF，与式(1)所得理论值11.13 pF相比，二者的相对误差仅为0.09%。当外层球体半径大于内层球体半径的20倍时，仿真所得电容与理论值的相对误差均在7%以下。因此可得利用CST电磁工作室仿真所得电容与理论值具有很好的一致性，因此采用类比的方式计算飞行状态下的飞机电容。

如图3所示，在CST电磁工作室中导入1∶1飞机仿真模型，将内层球体替换为飞机，进而计算飞行状态下飞机电容。根据图2所得结论，当外层球体半径为内层球体半径的20倍以上时，相对误差较小。飞机的半翼长为8.36 m，因此设置外层球体半径为168 m。仿真得到飞行状态下飞机的电容约为460.5 pF。

图3 飞行中的飞机电容计算Fig.3 Aircraft capacitance calculation in flight

为进一步验证仿真所得飞机电容的正确性，根据文献[2]中飞机电容的经验公式：

CG=21.3X

(3)

CF=0.315CG

(4)

式中：X为飞机的翼长，ft(1ft=304.8 mm)；CG为飞机的接地电容；CF为飞机在飞行状态下的电容，pF。

由文献[2]可知，翼长为12.80 m(42 ft)的飞机接地电容(CG)为925 pF，由此推算翼长为16.72 m(55 ft)飞机的接地电容为1 171.5 pF。将接地电容代入式(4)计算得CF为369.1 pF。由式(4)计算所得飞机电容与CST仿真所得飞机电容的误差为24.76%，二者具有可比拟性，进而验证了利用仿真获取飞机电容的方法是可取的。

3 飞机模型对飞机静电分布的影响分析

为了考察不同模型对飞机沉积静电电荷与电场分布规律的影响，建立2种飞机模型，分别为简化模型和细化模型，如图4所示。简化模型在细化模型的基础上省略驾驶舱、机舱舷窗和引擎结构。为对比不同飞机模型上同一位置处的电荷与电场，在2模型上选取了几处典型位置，如图4所示。

图4 飞机模型Fig.4 Aircraft model

分别对2个模型施加相同的电压100 kV，仿真该电压作用下飞机表面的电荷密度及电场强度。两模型的机身材料均为PEC，驾驶舱与机舱舷窗材料为铅玻璃，背景材料为空气。仿真所得飞机表面电荷密度和表面电场强度分别如图5、图6所示。

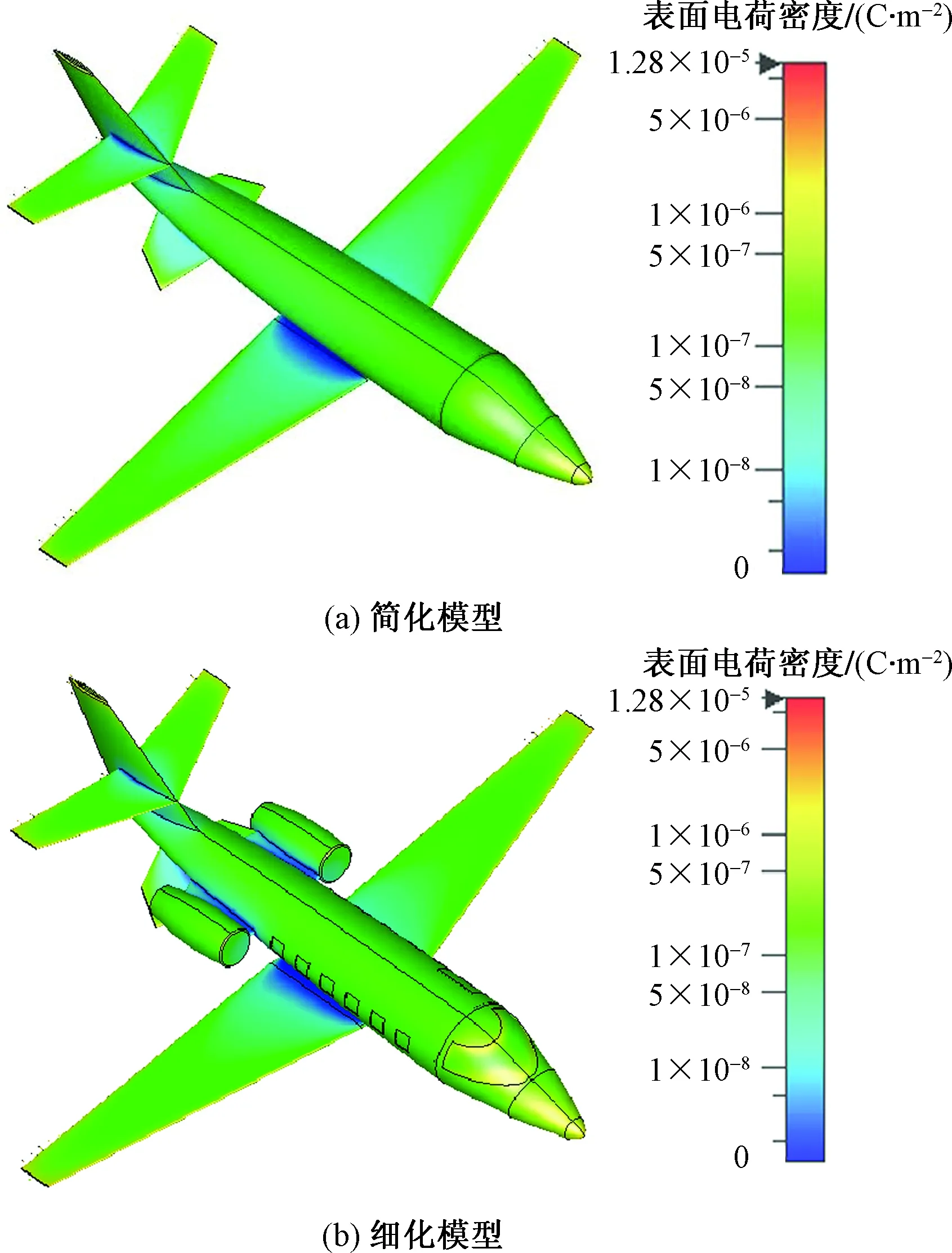
图5 不同模型的表面电荷密度分布Fig.5 Surface charge density distribution of different models

图6 不同模型的表面电场强度分布Fig.6 Surface electric field intensity distribution of different models

由图5、图6可知，2个模型表面电荷密度与表面电场强度分布规律相近，在飞机尖端部位表面电荷密度与表面电场强度较大，如机身两侧机翼尖端、尾翼尖端、机头顶端；在驾驶舱与机舱的舷窗处、机身、机身与机翼连接处的表面电荷密度与表面电场场强较小。为进一步证明不同飞机模型对飞机沉积静电分布的影响，将图4中所标记位置处的表面电荷密度和表面电场强度的仿真结果列于表1和表2中，其中，百分比差异计算公式为

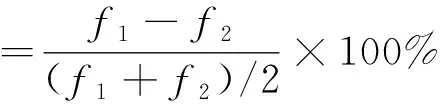
(5)

式(5)中：f1、f2为计算差异时二者的取值。

由表1和表2可知，细化模型与简化模型相比，在机头尖端位置A的表面电荷密度与表面电场强度的变化量为20%左右，变化较明显。说明加入驾驶舱后使得电荷集中向机头尖端移动，使机头尖端的表面电场强度增高。同时，由表1和表2可知，细化模型机头A位置处的表面电场强度与表面电荷密最高，而简化模型放电刷2位置处的表面电场强度与表面电荷密度不是最高。这说明驾驶舱对机头尖端处的电荷分布规律有较大影响。

在机身与机翼连接位置E处，细化模型与简化模型相比，表面电荷密度与表面电场强度的变化量大于12%。说明加入引擎后部分电荷被转移到了引擎表面，这导致位置E处细化模型的表面电荷密度与表面电场强度减小。位置E处与其他位置处的表面电荷密度与表面电场强度相比，其在简化模型与细化模型中均最低。虽然此处的表面电荷密度与表面电场强度变化量较大，但对飞机静电放电影响较小。

表1 不同位置处的表面电荷密度Table 1 Surface charge density at different locations

表2 不同位置处的表面电场强度Table 2 Surface electric field intensity at different locations

在飞机机身、机翼、尾翼及放电刷等位置，两种模型的表面电荷密度与表面电场强度差别均在6%以下，这说明驾驶舱、机舱舷窗和引擎结构对飞机机身、机翼、尾翼及放电刷处的表面电荷密度与表面电场强度影响较小。同时，细化模型与简化模型相比，其飞机机身、机翼、尾翼及放电刷等位置处的表面电荷密度与表面电场强度的分布规律保持不变。

根据上述分析可得，细化模型加入驾驶舱、机舱舷窗、引擎结构后，对机头处的静电场有较大影响，而对其他位置的影响较小。因此，仅研究放电刷处的静电场分布时，可采用简化模型以提高仿真效率。

4 沉积电荷量对飞机放电刷处静电分布的影响分析

飞机飞行过程中其表面与空气中的粒子发生碰撞从而不断积累电荷，因此其产生的电场强度不断地增加。当其电场强度高于周围空气的击穿场强时，将会发生放电现象。为避免发生飞机静电放电，放电刷将提前泄放飞机表面的沉积静电。因此放电刷处的沉积静电分布规律对飞机沉积静电放电的研究至关重要。

基于飞机细化模型研究不同电压下放电刷处的沉积静电分布。飞机模型左右两侧对称，因此仅分析其中一侧放电刷处的电场强度。如图7所示，飞机放电刷位于飞机机翼尖端部位a处、飞机水平尾翼b处、飞机竖直尾翼c处、机尾尖端部位d处。其中放电刷1和放电刷9与机翼成45°，放电刷2～8、10～11垂直于机翼。

在标准大气环境下，均匀电场中空气击穿强度为29 kV/cm[13]。飞机通常飞行在10 000 m以上的高空中，例如当飞机飞行在16 000 m时，此时空气临界击穿场强为419 kV/m[18]。为了比较不同位置放电刷处电场强度的大小，当飞机表面沉积静电产生电压为150 kV时，不同位置处放电刷处平均电场强度的仿真结果如图8所示。

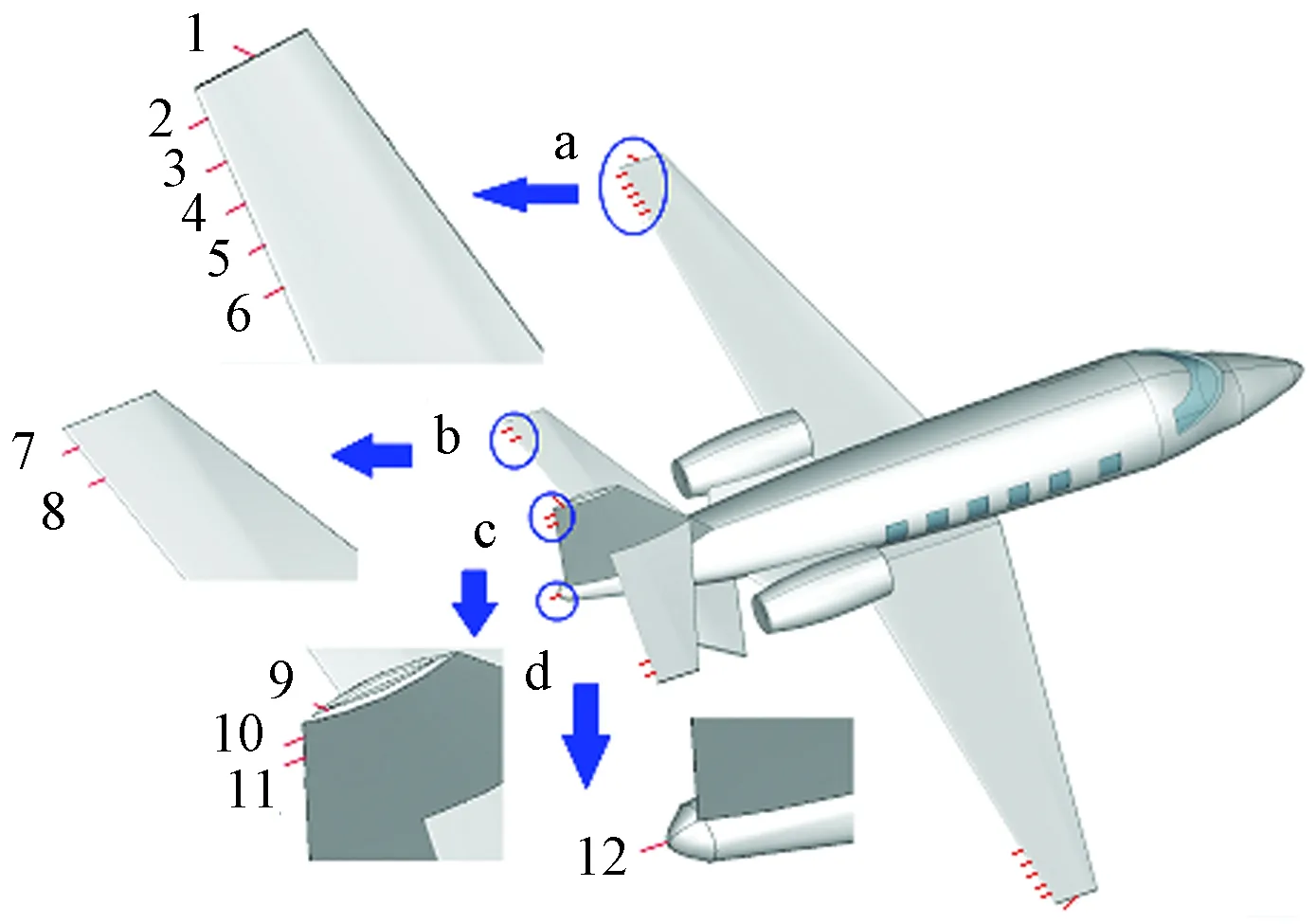
图7 放电刷监测位置Fig.7 Monitoring position of discharge brush

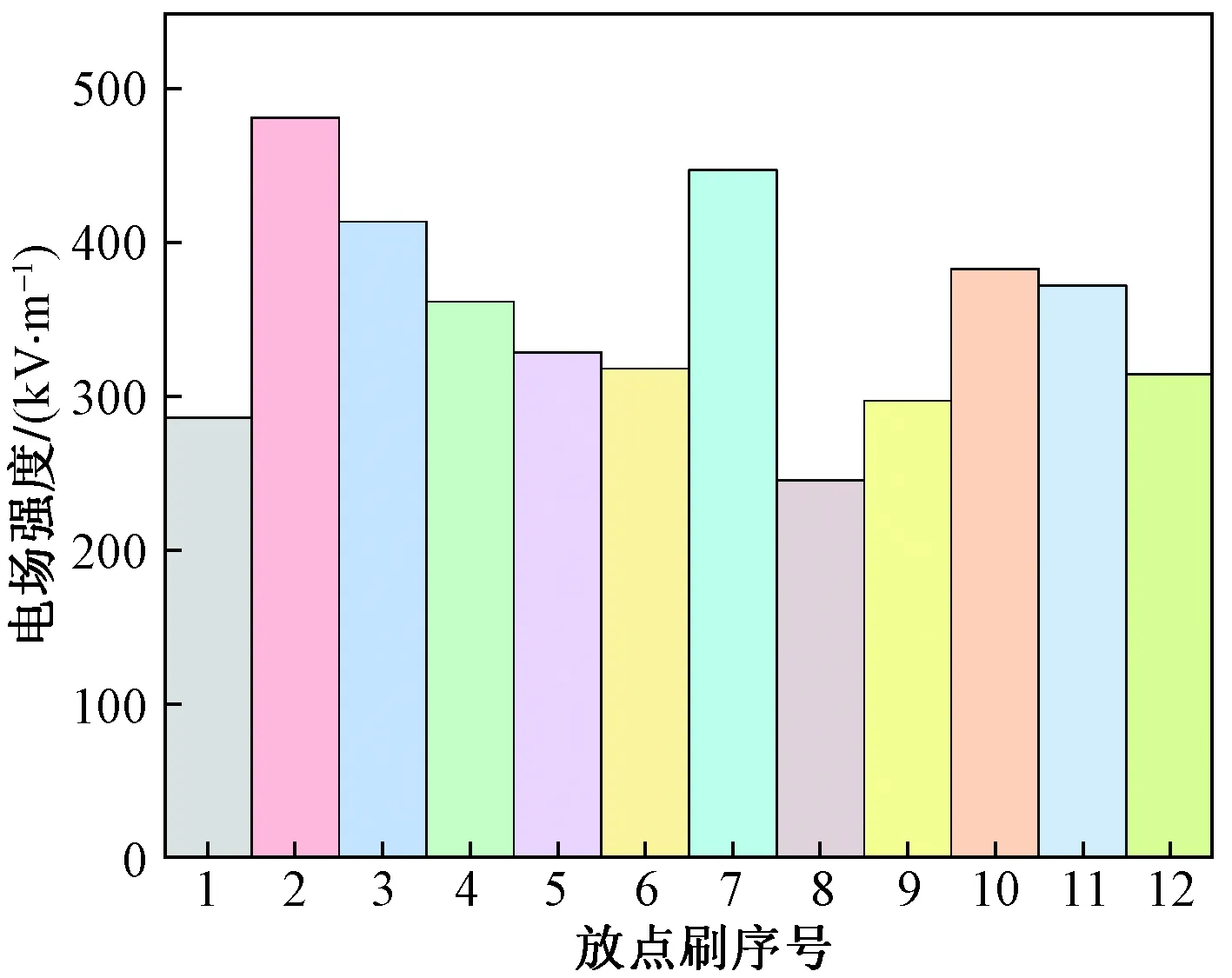
图8 150 kV下不同位置处放电刷的电场强度Fig.8 Electric field intensity of the discharge brush at different locations under 150 kV

由图8可知，飞机机翼尖端部位a处放电刷2的电场强度最高，为482 kV/m，飞机水平尾翼b处放电刷7次之，为471 kV/m，二者均超过空气临界击穿场强。飞机水平尾翼b处放电刷8的电场强度最低，为245 kV/m。放电刷2的电场强度比放电刷8高约97%。按照电场强度由高到低依次为放电刷2、7、3、10、11、4、5、6、12、9、1、8。这说明当发生飞机沉积静电放电时，放电刷2将先于其他放电刷开始放电。

通过仿真得到各放电刷处电场强度达到空气临界击穿场强时，所需的飞机沉积静电产生电压，如图9所示。不同放电刷处电场强度到达空气临界场强时所对应的飞机沉积静电电压不同。当飞机沉积静电产生电压为131 kV时，放电刷2的电场强度便达到空气临界击穿场强。当飞机沉积静电产生电压为140 kV时，放电刷7的电场强度达到空气临界击穿场强。当飞机沉积静电产生电压为256 kV时，放电刷8的电场强度才达到空气临界击穿场强。当发生空气击穿时，放电刷2所需的静电产生电压比放电刷8低约95%。这说明不同的飞机沉积静电电压下，发生放电的放电刷数量不同。当飞机沉积静电电压为131 kV时，放电刷2已开始放电，随着飞机沉积静电电压的增大，开始放电的放电刷数量逐步增加。

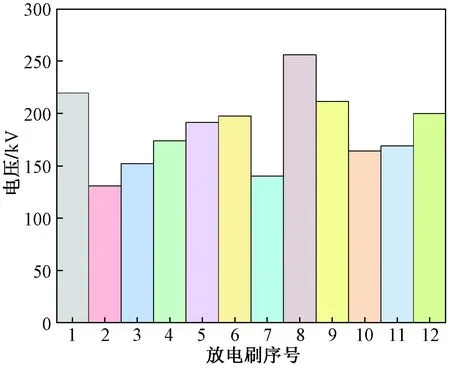
图9 发生空气击穿时飞机沉积静电电压Fig.9 Aircraft deposited electrostatic voltage when air breakdown occurs

为了分析不同飞机沉积静电电压下，飞机机翼尖端部位a处、飞机尾翼b、c处不同放电刷的电场强度规律，放电刷1～6的电场强度图10所示，放电刷7～11的电场强度如图11所示。

由图10可知，不同放电刷处的电场强度随着飞机沉积静电电压的增加而增加，且呈线性变化。放电刷2的电场强度最高，放电刷1的电场强度最低。放电刷2的电场强度随飞机沉积静电电压的变化率高于其他放电刷，按照变化率由高到低依次为放电刷2、3、4、5、6、1。放电刷2的电场强度随着静电电压的变化率比放电刷1高约68%。放电刷2的电场强度高于放电刷3～6，放电刷2的电场强度随着静电电压的变化率比放电刷6高约51%。由图11可知，放电刷7的电场强度高于放电刷8。放电刷7的电场强度随着静电电压的变化率比放电刷8高约82%。同时放电刷10的电场强度略高于放电刷11。这表明垂直于机翼的放电刷中，越靠近机翼尖端的放电刷电场强度越大。

由图10可知，放电刷1的电场强度低于放电刷2～6，放电刷1的电场强度随着静电电压的变化率比放电刷6低约11%。同样，由图11可知，放电刷9的电场强度低于放电刷10、11。放电刷9的电场强度随着静电电压的变化率比放电刷11低约25%。因此可得，与机翼成45°放电刷的电场强度低于同机翼的垂直放电刷电场强度。

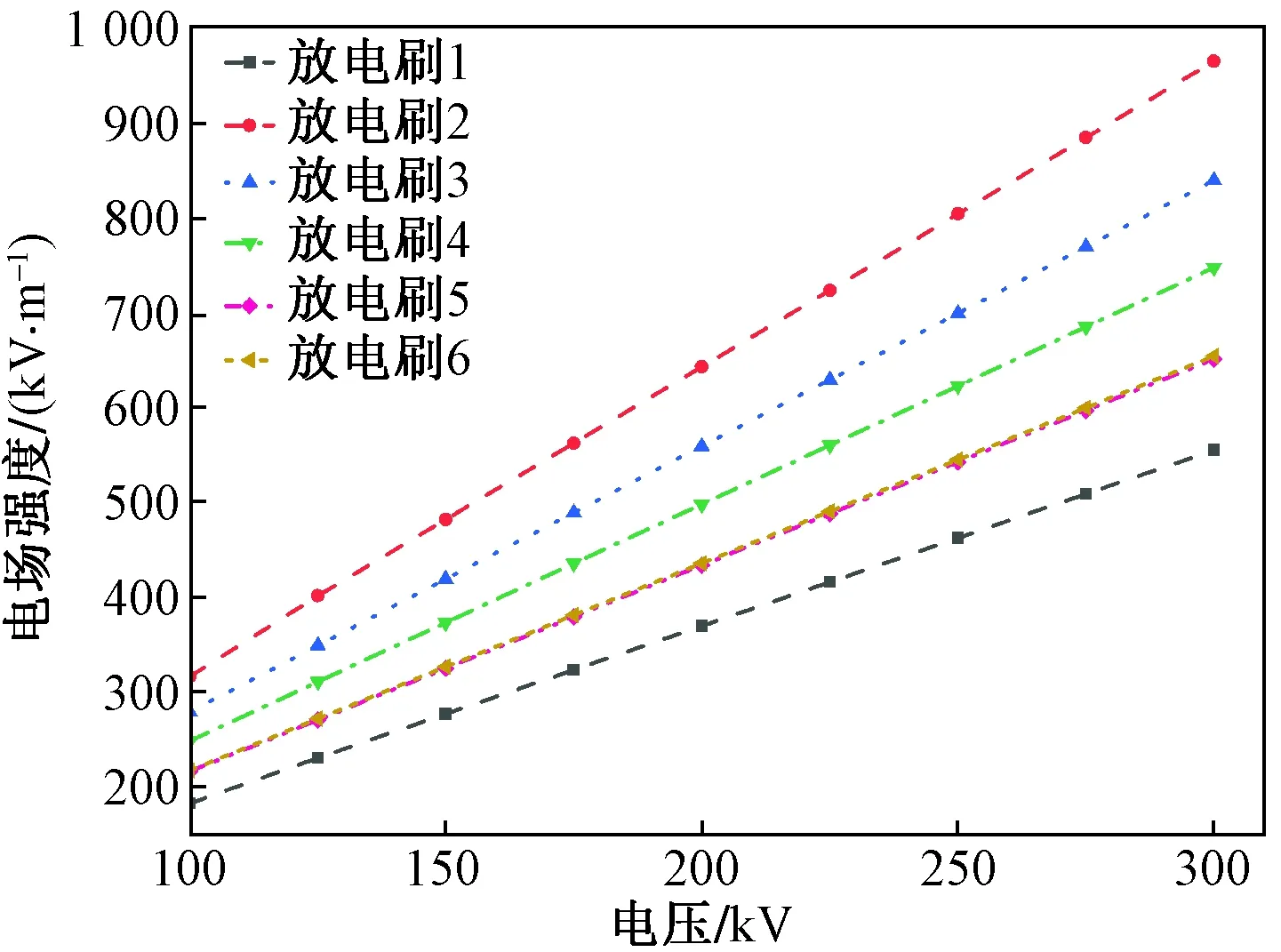
图10 机翼尖端部位a处放电刷的电场强度Fig.10 Electric field intensity of the discharge brush at a of the wing tip

图11 尾翼b、c处放电刷的电场强度Fig.11 Electric field strength of the discharge brushes at tail b and c

5 结论

建立了1∶1的飞机飞行状态下的静电场仿真模型，基于此模型仿真了飞机电容、飞机沉积静电电荷密度与电场分布，得到以下结论。

(1)通过类比球体电容的方法，对飞机电容进行了计算，得到飞行状态下飞机的电容为460.5 pF。

(2)模型对飞机机头处的静电场有影响，增加驾驶舱、机舱舷窗后，机头处的静电场变化了约20%，而对其他位置处的影响较小。若重点关注飞机放电刷处的静电场分布规律，可使用简化模型以提高仿真效率。

(3)在不同沉积静电电荷量下，飞机的各放电刷处的平均电场强度呈线性变化规律，飞机各放电刷处静电场强度不同，其中放电刷静电场强度最高处比最低处高约97%。对于垂直于机翼的放电刷中，越靠近机翼尖端的放电刷电场强度越大。垂直于机翼的放电刷处的电场强度高于同机翼的与机翼成45°放电刷处的电场强度。