ANCF/CRBF 平面梁闭锁问题及闭锁缓解研究1)
张大羽 罗建军 王辉 马小飞
∗(中国空间技术研究院西安分院,西安 710000)
†(西北工业大学航天学院,航天飞行动力学技术重点实验室,西安 710072)
引言
柔性梁被广泛地应用于航天与机械系统,是柔性多体系统动力学最典型的一类研究对象,建立其动力学模型可为复杂柔性多体系统设计和分析提供重要的理论依据.建立柔性梁模型的关键是如何准确地描述梁单元连续的旋转场,特别是当柔性梁经历大转动大变形运动.区分不同类型的非线性柔性梁建模方法的一个重要特征是如何准确地描述系统中的有限转动[1-10].
共旋坐标法[11-15]在处理有限转动时通过非线性迭代求解无限小的转动矢量,并将计算的转动增量叠加到方向余弦矩阵上.但是这类方法在求解时必须确保迭代步长不能过大,这样才能将转动增量近似为小转动的定轴旋转.此外,共旋坐标法将全局位移场分解为刚体运动和弹性变形,使得单元的惯性力等首先定义在迁移坐标系内,而后再转换到全局坐标系,同样要求了该方法的迭代步长不能过大.但是,过小的迭代步长会造成系统运动方程的线性化,导致柔性体在其纯刚体运动下产生非零的应变能,因此共旋坐标法仅适合用于模拟具有小应变的系统.几何精确梁方法[16-19]采用惯性坐标系下的节点绝对位移来描述结构的整体运动,不再对刚体运动和弹性运动进行区分,避免了增量法中的线性化问题,因此可以处理柔性梁的大变形问题.几何精确梁方法采用绝对位置向量和有限转角参数作为节点坐标,位移场和旋转场采用两个独立的插值函数,其中对有限转动插值方法的研究是该方法研究的一个重要分支.对于几何精确梁独立的旋转场插值策略,Shabana 和Ding[20]指出该策略会导致坐标的冗余及梁内同一物质点在位移场和转动场上的几何构型不一致,并通过算例证明了采用两个独立的插值函数表述位移和转动会导致梁在同一时刻存在两种不同的构型,与刚体动力学假设不相符.相比独立的旋转场插值,Shabana[21]提出了绝对节点坐标法(absolute nodal coordinate formulation,ANCF),该方法采用统一的插值函数描述梁内物质点的位置和转动.通过惯性坐标系下的梯度向量描述柔性体的方向,避免了对转角参数的相加运算,致使求解过程为非增量形式,这点区别于几何精确梁方法.此外,该方法还具有常数质量阵及不存在科氏力和离心力项的优点,适用于解决大转动大变形的柔性体的建模问题.近年来,绝对节点坐标方法已受到越来越多的学者的关注与研究[22-30,53-55].
绝对节点坐标法采用梯度向量描述柔性体转动和应变,虽然可以描述系统运动过程中的大转动大变形,但也存在一些缺陷.首先,相比转角参数,梯度向量不具有明确的转动物理意义,不利于面向单元旋转的设计和控制.例如,在变形过程中梯度变化方向不代表实际的系统旋转方向,对梯度向量的控制最终未必得到想要控制的转动量.其次,相比转角,梯度向量的数量更多,导致系统自由度的升高,以至加重系统计算负担.2015 年Shabana[31]提出基于一致旋转场列式的绝对节点坐标单元(ANCF consistent rotationbased formulation,ANCF/CRBF).该单元在统一的位移场和旋转场描述基础上,通过速度转换矩阵将梯度向量由转动参数替代,成功引入了转角坐标,解决了上述缺陷.此外,ANCF/CRBF 单元采用统一的插值函数解决了位移场和旋转场分开插值策略而导致坐标和几何构型冗余的问题.例如,线性插值的位移场得到零曲率,而线性插值的转动场得到高度非线性曲率,导致单元的曲率定义不统一.随后,Zheng 等[32]建立了ANCF/CRBF 平面梁单元,并进行了单元动力学分析.
但是,已有ANCF/CRBF 梁在ANCF 全参数平面梁的框架上开发的,同样存在严重的闭锁问题,特别是泊松闭锁,会给数值计算带来困难.ANCF 单元泊松闭锁问题产生的原因是单元的轴向高阶插值和横向低阶插值不一致导致不同方向间的应力相互耦合,致使单元在弯曲过程中由轴向的弯曲变形高阶项产生出伪应力,导致单元性能下降,呈现出“弯曲锁死”的现象.对于传统ANCF 全参数梁单元的泊松闭锁问题及其缓解技术,典型的研究有:Gerstmayr等[33]采用缩减积分方法(selectively reduced integration method,SRIM)重新构造了平面梁单元的弹性力矩阵,选择性地避开了对弯曲变形的高阶项的积分,可以有效缓解泊松闭锁.Mikkola 等[34]在平面ANCF梁单元基础上采用对横向变形场独立插值技术,提出了一种基于混合插值的平面ANCF 梁单元.动力学仿真结果表明该单元具有更高的弯曲变形精度和收敛性.Schwab 和Meijaard[35]采用弹性线方法(elastic center line,ECL)构造了新的弹性力公式,消除了轴向与横向变形间的高阶耦合项,缓解了泊松闭锁问题.此外,Schwab 和Meijaard[35]分别采用基于Hellinger-Reissner 和Veubeke-Hu-Washizu 变分原理的方法用于消除三维ANCF 全参数梁单元剪切闭锁问题,改善了单元的弯曲性能.Hussein 等[41]采用Hellinger-Reissner 方法消除了二维ANCF 全参数梁单元的剪切闭锁问题,并分别测试了Hellinger-Reissner 方法在薄梁和厚梁动力学分析中消除闭锁的效果.李文雄等[42]提出基于Hellinger-Reissner 变分原理的无闭锁曲梁单元.与常规曲梁单元相比,该单元具有更高的精度和效率.Patel 和Shabana[36]提出了的一种全新的缓解单元泊松闭锁的方法,应变分解方法(strain split method,SSM).其核心是将应变分解为单元轴向应变和截面应变,这样可将由泊松效应引起的轴向弯曲变形高阶项与截面变形项区分出来,然后分别施加相应的弹性矩阵,将泊松效应仅计入到轴向上,进而起到泊松闭锁缓解作用.缩减积分方法和弹性线方法都是从单元积分角度选择性地避开计算应变−应力关系的高阶耦合项,这两种方法适用于缓解单元的泊松和剪切闭锁;基于多场变分原理是从单元位移场角度引入单独的剪切场插值函数,从而消除横截面剪切变形与轴向拉伸和弯曲变形的耦合项,该方法主要用于解决单元的剪切闭锁问题;应变分解方法是从单元运动学角度将高阶耦合项解耦出来,从而仅将泊松效应施加在应变−应力关系的低阶线性项上,该方法用于解决单元的泊松闭锁问题.对于ANCF/CRBF单元的泊松闭锁问题鲜有研究,对该单元闭锁问题的深入探讨是十分必要的,有助于提升单元的计算精度和确定单元的应用范围.
本文系统研究了ANCF/CRBF 单元特有的泊松闭锁问题及其缓解技术.ANCF/CRBF 梁单元的推导是通过对ANCF 梁单元的节点处横截面施加运动学约束得到的.由于约束后的横截面不能变形,消除了节点处的泊松闭锁,但是非节点处仍然存在泊松闭锁.这将导致ANCF/CRBF 梁单元与ANCF 梁单元不同的泊松闭锁特性,同时也使得泊松闭锁成为ANCF/CRBF 单元主要的闭锁问题.首先,为了全面地理解ANCF/CRBF 梁单元特有的泊松闭锁特性以及深入探索施加运动学约束对ANCF/CRBF 梁单元泊松闭锁特性的影响,在已有ANCF/CRBF 刚性截面梁的基础上,进一步对单元的轴向梯度进行约束,建立了两种新的刚性截面的ANCF/CRBF 梁单元.新单元在节点处完全消除了泊松闭锁和剪切效应,这是与传统ANCF/CRBF 刚性截面梁单元的不同之处.然后,采用两种闭锁缓解技术,弹性线方法和应变分解方法,提升了ANCF/CRBF 单元的收敛性和计算精度.以期为ANCF/CRBF 这类单元的闭锁问题分析以及单元的应用范围提供参考数据.
1 传统的ANCF 全参数平面梁单元
传统的ANCF 全参数平面梁单元是绝对节点坐标方法中的经典单元,其采用统一的插值函数描述单元的平动和转动.该单元在运动过程中横截面与梁轴线不保持时刻垂直,截面可变形.
1.1 单元运动学描述

ANCF12 单元采用统一的插值策略,这会导致梁的轴向弯曲变形高阶项与横向低阶变形高度耦合,产生严重的泊松闭锁问题,致使计算精度下降.此外,ANCF12 单元采用梯度坐标描述单元的转动信息,但是它的物理意义不如转角参数明确.
1.2 单元弹性力公式

图1 三种变形构型之间的关系Fig.1 Three general configurations
梁单元i的Green-Lagrange 应变张量εi可通过变形梯度张量Ji得到

其中,λ=Eν/[(1+ν)(1 −2ν)],µ=E/[2(1+ν)];E是弹性模量,ν 是泊松比.
1.3 单元动力学方程

2 ANCF/CRBF 平面梁单元
传统ANCF 全参数平面梁单元采用梯度坐标描述单元的转动信息,但是其物理意义不如转角参数明确,并且采用梯度坐标会使单元的广义坐标数目增多,导致动力学计算效率降低.基于一致旋转场列式的ANCF/CRBF 单元的提出可以解决以上问题.下面分别介绍已有的ANCF/CRBF 平面梁单元,以及本文新开发的两种刚性截面ANCF/CRBF 平面梁单元.
2.1 传统的ANCF/CRBF 刚性截面梁单元


2.2 ANCF/CRBF 轴向不可伸展的刚性截面梁单元

对于梁单元i的转换关系如下[43]


2.3 ANCF/CRBF 轴向可伸展的刚性截面梁单元

对于梁单元i的转换关系如下[43]
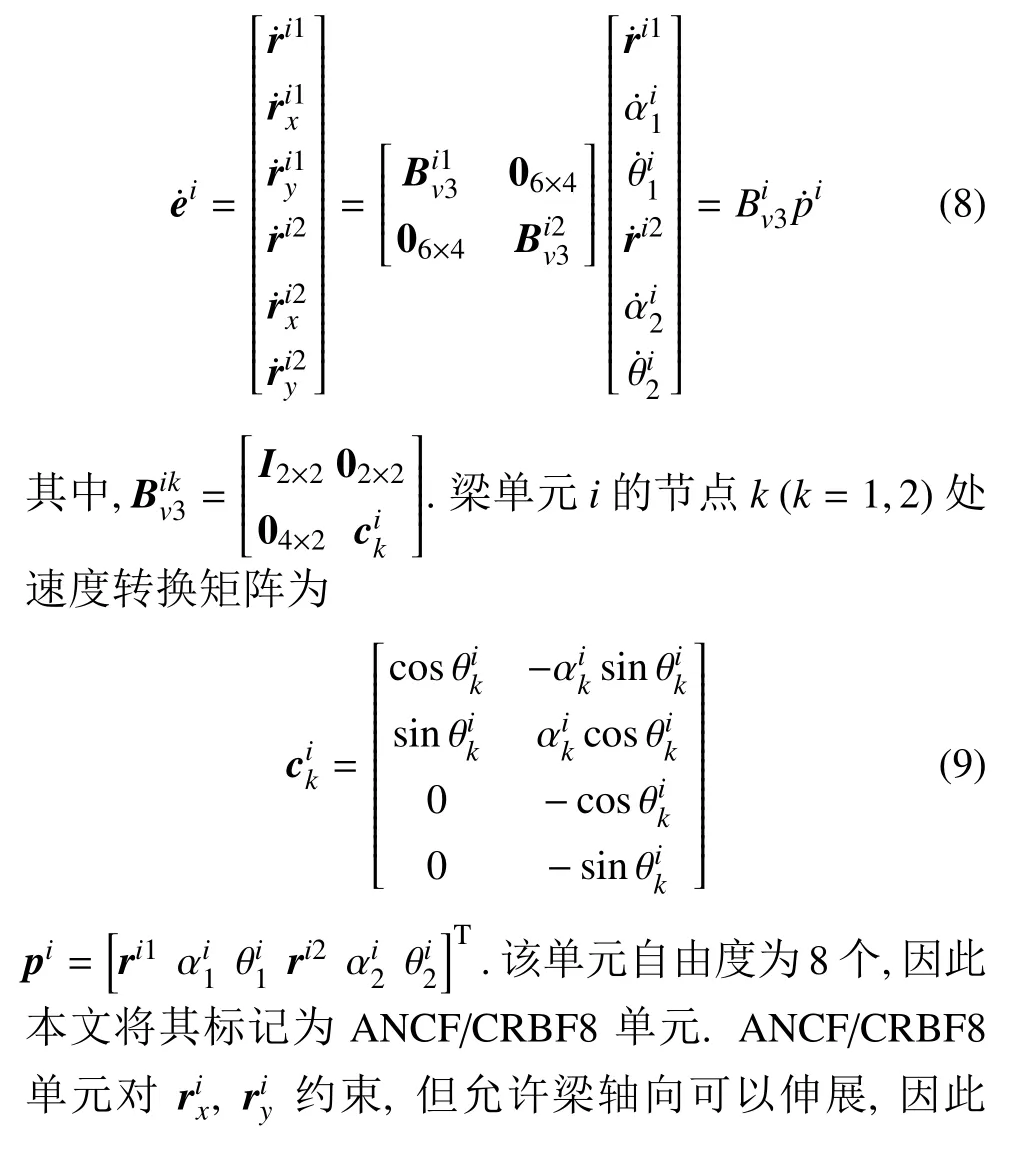

2.4 单元动力学方程

值得注意的是,ANCF/CRBF 单元计算转角是通过积分角度对时间的导数得到的,而非积分角速度.分空间和平面两种情况进行讨论.
(1)在空间情况下,以全参数ANCF 梁单元与ANCF/CRBF 梁单元转换为例,其速度层面的转换关系为[31,44-45]


文中还指出ANCF/FFR 单元虽然可准确描述初始弯曲构型,有利于开发一种基于力学的计算机辅助设计和分析(I-CAD-A)融合方法.但是,由于引入了小转动坐标会导致这类单元不能精确地表示刚体惯性,会影响单元的动力学精度.因此对ANCF/FFR单元的闭锁缓解技术研究可作为下一步研究的方向.
3 单元闭锁缓解技术
ANCF 全参数平面梁单元存在着严重的泊松闭锁问题,会严重影响单元的计算精度.针对如何缓解ANCF 单元泊松闭锁问题,已有大量地研究,其中典型的方法有弹性线方法和应变分解方法.本节对两种方法进行逐一介绍.
3.1 弹性线方法
由弹性线方法(ECL)可知[21,35],应变势能通过对沿中心轴线xi积分得到,由轴向拉伸势能剪切势能和横向弯曲势能组成
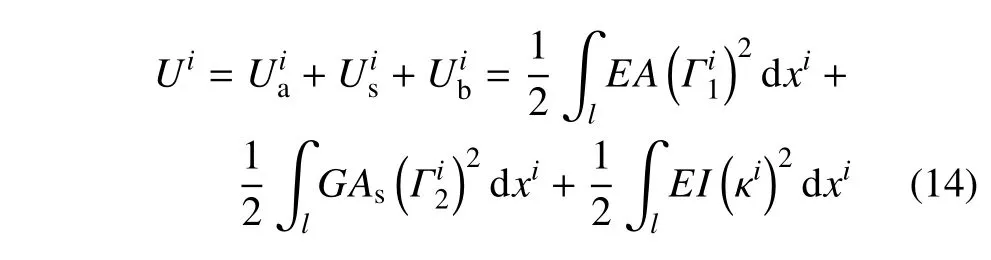
其中,E,G,A,I分别是弹性模量、剪切模量、横截面面积和截面惯性矩.剪切模量表示为G=E/[2(1+ν)].As=ks·A,其中,ks是剪切修正因子.对于横截面是矩形的情况,ks=10(1+ν)/(12+11ν).对于轴向应变、剪切应变、及曲率公式κi分别可表示为

在弹性线方法中,由于仅对梁轴向中心线进行积分,一定程度上可以缓解由高阶弯曲变形和低阶横向变形耦合引起的闭锁问题.弹性线方法适合用于计算较薄的直梁结构.
3.2 应变分解方法
由应变分解方法(SSM)可知[36],对于梁单元i,其位置和梯度向量可分解为
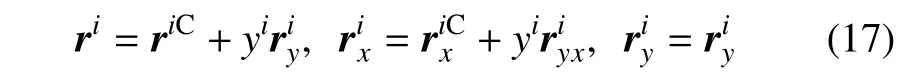


依据Voigt 标记规则,可写为

对于ANCF 全参数平面梁单元,从式(20)分析得知,其弯曲变形的高阶项在单元非轴向分应变εiS中,会产生伪应力,这是导致单元泊松闭锁的原因.因此,在求解第二类Piola-Kirchhoff 应力时对两个Green-Lagrange 分应变εiC,εiS分别施加不同的弹性矩阵,可表示为σ=EiCεiC+EiSεiS,其中弹性矩阵分别为
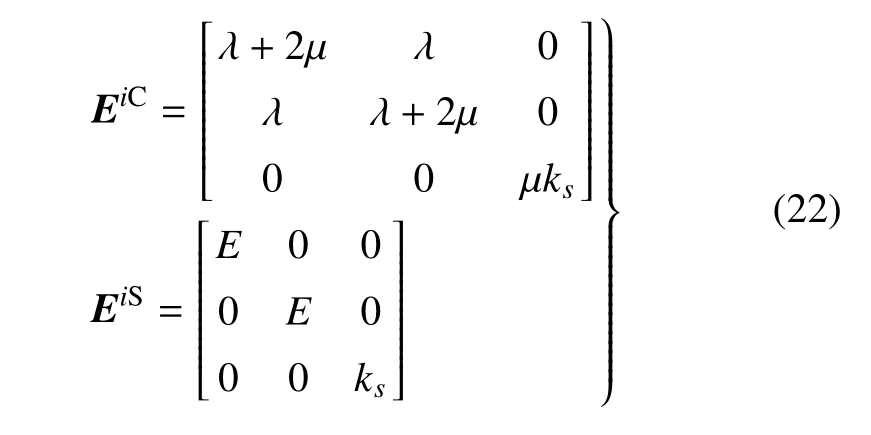
由式(22)可以看出,应变分解方法将泊松效应仅施加在低阶轴向分应变εiC上,可有效地将梁横截面低阶正应变与由弯曲变形高阶项引起的伪应变分离开来,使得泊松效应充分地体现在低阶正应变中,有效地缓解了ANCF 梁单元泊松闭锁问题.在应变分解方法中,梁单元的弹性力向量可计算为
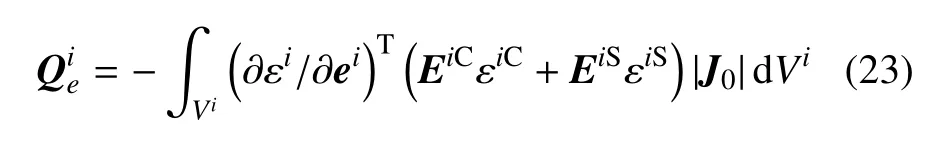
4 算例分析
本文设计5 种算例用于全面测试新单元的性能,分别是小变形细长梁静力学算例、大变形深梁静力学算例、悬臂梁末端受弯矩静力学算例、悬臂梁受重力动力学算例和柔性单摆动力学算例.此外,本文还对两种闭锁缓解技术应用在新单元上的效果进行研究.为了方便对比分析,仿真中的模型可归纳为10种类型,分别是:
(1)ANCF12-GCM (传统ANCF 全参数梁单元+连续介质力学);
(2)ANCF/CRBF10-GCM (传统刚性截面ANCF/CRBF 梁单元+连续介质力学);
(3)ANCF/CRBF10-ECL (传统刚性截面ANCF/CRBF 梁单元+弹性线方法);
(4)ANCF/CRBF10-SSM (传统刚性截面ANCF/CRBF 梁单元+应变分解方法);
(5)ANCF/CRBF8-GCM(轴向可伸展的刚性截面ANCF/CRBF 梁单元+连续介质力学);
(6)ANCF/CRBF8-ECL (轴向可伸展的刚性截面ANCF/CRBF 梁单元+弹性线方法);
(7)ANCF/CRBF8-SSM (轴向可伸展的刚性截面ANCF/CRBF 梁单元+应变分解方法);
(8)ANCF/CRBF6-GCM(轴向不可伸展的刚性截面ANCF/CRBF 梁单元+连续介质力学);
(9)ANCF/CRBF6-ECL (轴向不可伸展的刚性截面ANCF/CRBF 梁单元+弹性线方法);
(10)ANCF/CRBF6-SSM(轴向不可伸展的刚性截面ANCF/CRBF 梁单元+应变分解方法).
根据第2 节和第3 节对绝对节点坐标全参数梁和基于一致旋转场的绝对节点坐标梁单元的描述,详细分析各类型单元泊松闭锁的特点.
(1)ANCF12-GCM
①轴向可伸展、截面可变形;
②旋转描述中无转角参数,仅有梯度向量;
③节点处存在剪切变形;
④截面无约束,节点处和单元内均有泊松闭锁.
(2)ANCF/CRBF10-GCM
①轴向可伸展、截面不可变形;
②旋转描述中既有转角参数又有梯度向量;
③节点处存在剪切变形;
④节点截面全约束,节点处无泊松闭锁,单元内存在泊松闭锁.这种不连续情况导致单元整体的泊松闭锁问题相较ANCF12 单元更加严重.
(3)ANCF/CRBF8-GCM
①轴向可伸展、截面不可变形;
②旋转描述中仅有转角参数;
③节点处不存在剪切变形;
④节点截面全约束,节点处无泊松闭锁,单元内存在泊松闭锁.此外,节点处无剪切变形,单元内存在剪切变形.这种不连续情况导致单元整体的泊松闭锁相较ANCF10 单元更加严重.
(4)ANCF/CRBF6-GCM
①轴向不可伸展、截面不可变形;
②旋转描述中仅有转角参数;
③节点处不存在剪切变形;
④节点截面全约束,节点处无泊松闭锁,单元内存在泊松闭锁.此外,单元轴线不能伸展.这会导致单元整体的泊松闭锁相较ANCF8 单元更加严重.
4.1 静力学测试:小变形细长梁算例
该算例为典型的悬臂梁受集中载荷问题,考察ANCF/CRBF 单元在小变形静力学分析中的准确性.图2 所示为悬臂梁.梁的参数分别为长度l=1 m,高度和厚度h=w=0.01 m,弹性模量E=200 GPa,泊松比ν=0.3,以及末端集中力设为F=−10 N.采用Newton-Raphson 迭代求解其非线性方程组,相对误差设置为RelT=10−6.Y方向位移具有理论解为δ=−0.02 m.
表1 为不同单元类型采用连续介质力学方法时计算的Y向位移.首先,发现ANCF12 单元、ANCF/CRBF10 单元、ANCF/CRBF6 和ANCF/CRBF8 单元均不能收敛到理论解,这是因为采用连续介质力学方法计算的弹性力会造成轴向和截面的正应变高度耦合,使得泊松效应更加地明显.其次,ANCF 全参数平面梁单元和ANCF/CRBF 单元在小变形静力学问题上表现相当.表2 为不同单元类型采用闭锁缓解方法时计算的Y向位移.以ANCF/CRBF10 单元作为参考解,可以发现ANCF/CRBF6 和ANCF/CRBF8 单元的计算精度低于参考解.这是因为这两个单元都对节点处梯度向量进行了正交约束,可捕捉到的截面变形类型减少,所以计算精度不如传统ANCF 全参数单元.此外,约束截面虽然可以消除节点处的泊松闭锁,但单元内的截面可以变形,仍然存在闭锁问题.图3 所示为ANCF/CRBF8 单元采用三种弹性力计算方式下的Y向位移误差收敛率,可以发现在小变形情况下,采用弹性线方法或应变分解法时的收敛率相当.由于本算例的特色为细长梁,截面变形小,泊松闭锁问题不明显.下一个算例将采用深梁模型进一步研究单元的闭锁问题.
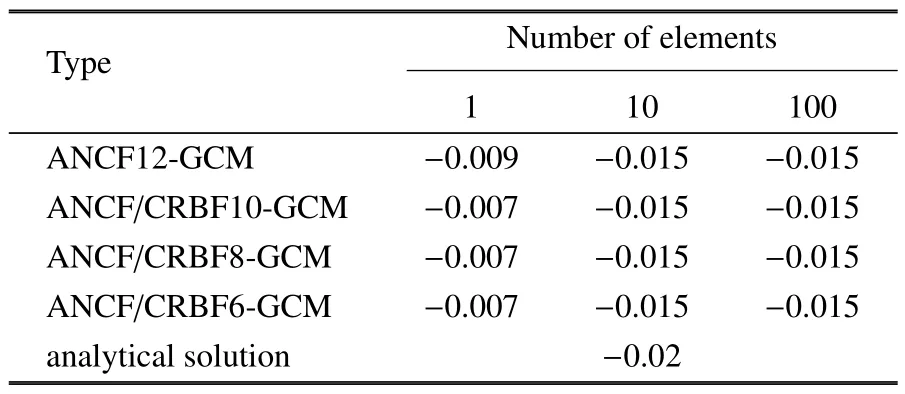
表1 小变形情况下Y 向位移对比(m)Table 1 Tip vertical displacement of beam in case of small deformation(m)
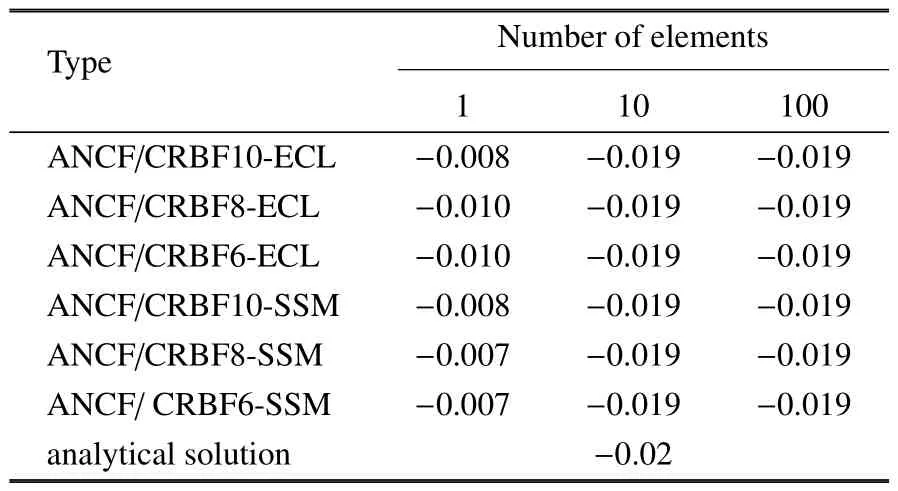
表2 小变形情况下Y 向位移对比(使用闭锁缓解技术)(m)Table 2 Tip vertical displacement of beam in case of small deformation using locking alleviation methods(m)
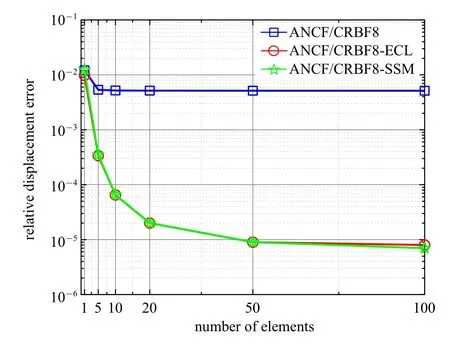
图3 ANCF/CRBF8 单元Y 向位移相对误差Fig.3 Relative error of tip vertical displacement of ANCF/CRBF8 beam in case of small deformation
4.2 静力学测试:大变形深梁算例
本算例采用深梁模型,如图2 所示.梁的参数分别为长度l=2 m,高度h=0.5 m 和厚度w=0.1 m,弹性模量E=207 GPa,以及泊松比ν=0.3.由于深梁的横截面有着较大的变形,可完全捕捉泊松效应,因此单元的泊松闭锁问题更加严重,该算例常被用于测试单元受较大变形时的静力学计算精度.为了验证大变形算例,设置末端集中力为F=−5.0×108×h3N,与文献[33]中的参数相同.采用Newton-Raphson 迭代求解其非线性方程组,相对误差设置为RelT=10−6.本算例中的参考解为采用商业有限元软件ANSYS 计算的数值收敛解δ=−0.713 420 m.
表3 为不同单元类型采用连续介质力学方法时计算的Y向位移.首先,以传统ANCF12 单元作为参考,发现ANCF/CRBF 单元由于对梯度向量施加了约束,消除了部分的变形模态,因此其计算精度不如ANCF12 单元.其次,发现两种刚性截面的ANCF/CRBF 单元的计算精度不如ANCF/ANCF10 单元.对于深梁结构,由于长宽比较小,梁内部的泊松闭锁更加严重,导致ANCF/CRBF 单元的静力学计算精度更差.另外,在ANCF/CRBF 单元中,对梯度向量约束的越多,静力学计算精度越差.因此,相比ANCF 全参数梁单元,ANCF/CRBF 单元不具有静力学计算优势,特别是对于大变形深梁结构.表4 为不同单元类型采用闭锁缓解方法时计算的Y向位移.对比发现仅有应变分解法计算的结果可收敛到数值解.图4 所示为ANCF/CRBF8 单元的Y向位移误差收敛率,发现在大变形情况下,应变分解法的收敛率最好.对于大变形深梁模型,截面泊松效应明显,应变分解法可将梁轴线方向正应变和截面方向正应变分解,可完全解除轴向高阶弯曲变形和截面低阶变形间的高度耦合关系,泊松效应仅计入在轴向正应变上.而弹性线方法仅可去除掉一些不重要的高阶项,但不能将轴向和截面变形解耦,单元仍然存在一定程度上的泊松闭锁,因此计算精度不如应变分解法的计算精度高.
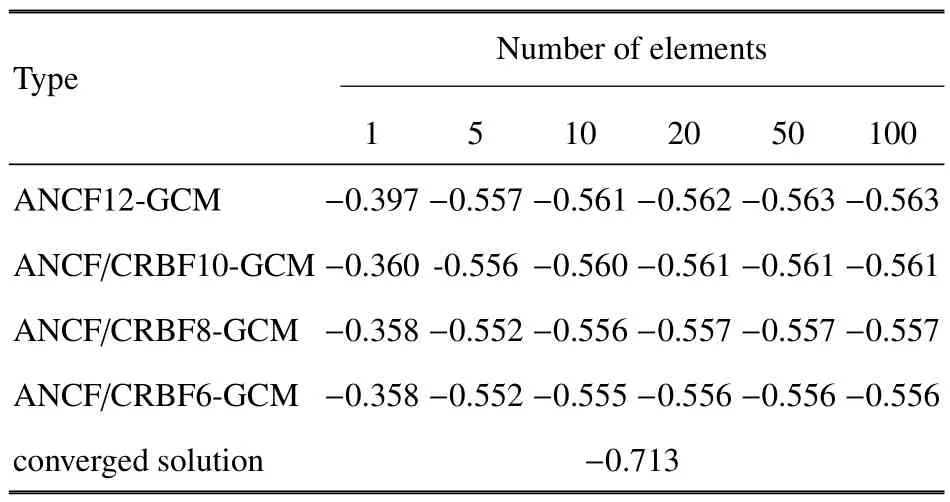
表3 大变形情况下Y 向位移对比(m)Table 3 Tip vertical displacement of beam in case of large deformation(m)

表4 大变形情况下Y 向位移对比(使用闭锁缓解技术)(m)Table 4 Tip vertical displacement of beam in case of large deformation using locking alleviation methods(m)

图4 ANCF/CRBF8 单元Y 向位移相对误差Fig.4 Relative error of tip vertical displacement of ANCF/CRBF8 beam in case of large deformation
4.3 静力学测试:悬臂梁受端部集中力矩算例
本算例验证ANCF/CRBF 梁单元在强几何非线性静力学分析中的有效性,如图5 所示.梁的参数分别为长度l=10 m,高度h=0.1 m 和厚度w=0.1 m,弹性模量E=210 GPa,以及考虑泊松效应,泊松比设为ν=0.3,与参考文献[18]相同.在梁的末端所施加的理论力矩为M=πEI/l.该算例具有理论解,当M=2πEI/l时,直梁最终被弯曲成一个圆.采用牛顿迭代法求解,相对误差设置为10−6,载荷迭代步数设为20.本算例弹性力的计算采用应变分解方法.分别采用ANCF12,ANCF/CRBF10,ANCF/CRBF8 和ANCF/CRBF6 模拟悬臂梁.为了全面测试ANCF/CRBF 单元承受弯曲的情况,所加载的弯矩由小到大,并分为多组进行测试.
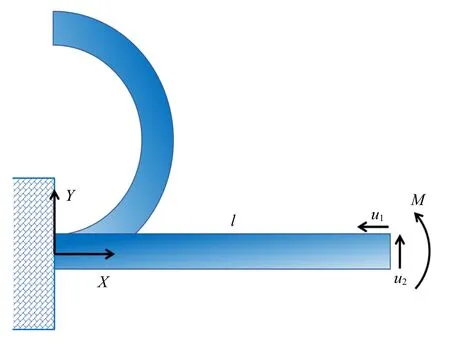
图5 悬臂梁末端受集中力矩作用Fig.5 Cantilever beam subjected by a torque
对于该强几何非线性静力学算例,对比表5 和表6 发现:首先,ANCF 单元由于存在闭锁问题,测试发现采用40 个单元划分梁模型才使得悬臂梁被弯成整圆(所受力矩为ML/(πEI)=2 时).其次,对三种ANCF/CRBF 单元进行测试,采用与ANCF 单元弯成整圆相同的单元数,发现ANCF/CRBF 单元在受载小弯矩时的结果与理论解相近(ML/(πEI)=0.2 ∼1.0).当弯矩增大,ANCF/CRBF 单元的结果开始与理论解呈现较大的偏差(ML/(πEI)=1.2 ∼2.0).图6 是ANCF 单元和ANCF/CRBF 单元在所受力矩为ML/(πEI)=2 时的构型图.


表5 梁末端X 向位移对比(m)Table 5 Comparison of tip axial displacement using strain split locking alleviation methods(m)

表6 梁末端Y 向位移对比(m)Table 6 Comparison of tip vertical displacement using strain split locking alleviation methods(m)

图6 悬臂梁受端部集中力矩下的构型图(40 个单元)Fig.6 Cantilever beam configurations subjected by a torque(40 elements)
根据从文献[45]可知,只有单元上两个节点之间的相对转动不超过30◦时,得到的可认为是单位向量,从而ANCF/CRBF 单元才有效.可以通过以下的计算证明:例如让单元的一个节点处的转角为0◦,另一个节点处的转角从0◦变化到360◦,计算ξ=0.5 处的范数中的误差,如图7 所示.可以得到,在两个节点相对转角为30◦时,误差为0.034,与文献[45]中的结论相符.此时ANCF/CRBF 单元的可近似认为单位向量,并且单元有效.但是当相对转角继续增大时,范数的误差也随之增大,这也解释了ANCF/CRBF 这类单元在承受较大力矩时计算精度差的原因.
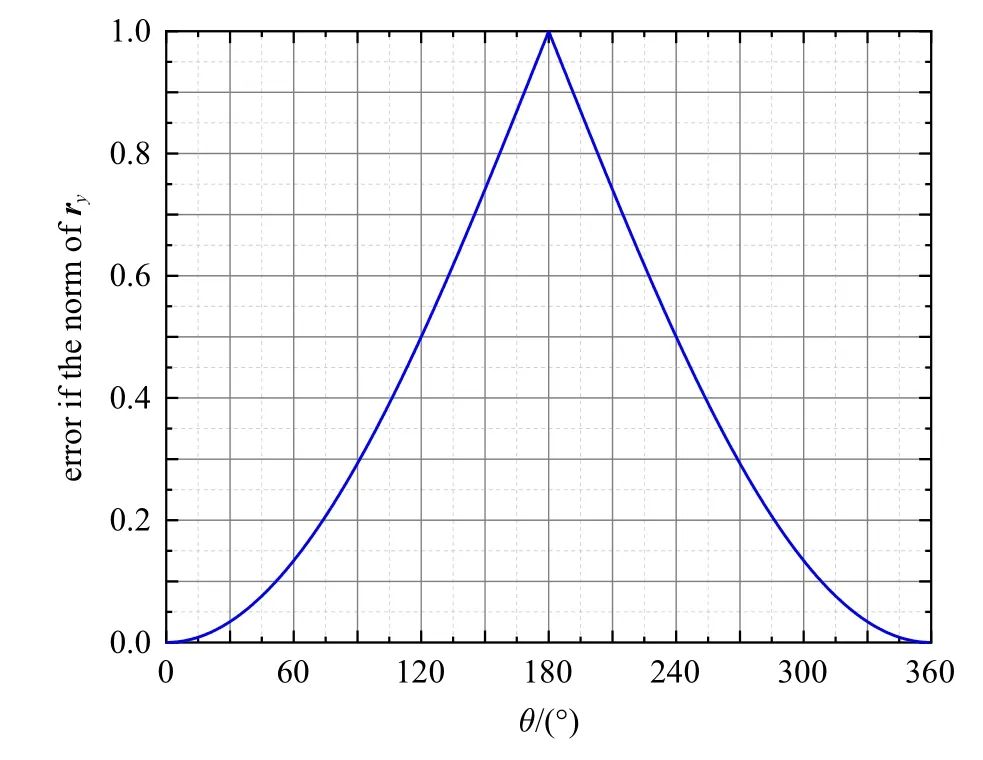
图7 ry 范数的误差Fig.7 Error of the norm of ry
4.4 动力学测试:悬臂梁受重力作用算例
本小节采用文献[39]中的悬臂深梁受到重力作用的算例,该算例专门用于分析泊松闭锁问题对单元动力学特性的影响,如图8 所示.本算例弹性力的计算分别采用连续介质力学方法、弹性线方法和应变分解方法.悬臂梁的参数分别为长度l=1 m,高度和厚度h=0.1 m,w=0.07 m,弹性模量E=60 MPa,密度ρ=7200 kg/m3,以及泊松比ν=0.3.在重力作用下,悬臂梁在XY平面内往复运动,仿真时间为1 s.柔性梁被划分为10 个单元.采用显式积分方法,轴向和横向的高斯积分点分别为5 个和3 个.
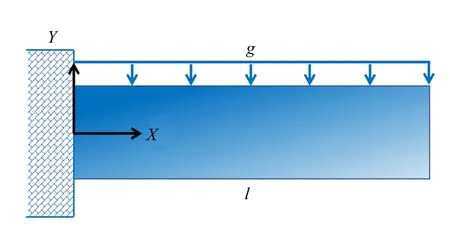
图8 悬臂梁动力学模型Fig.8 Cantilever beam dynamic problem
图9 为梁末端端点处X方向位移变化.可以看到当单元采用连续介质力学方法计算的弹性力时,单元泊松闭锁问题严重.当采用两种闭锁缓解技术均可以缓解闭锁问题.从静力学分析和本小节的动力学分析可以得到,应变分解方法既适用于细长梁结构也适用于深梁结构,是最有效的方法,而弹性线方法更适用于模拟细长梁结构.
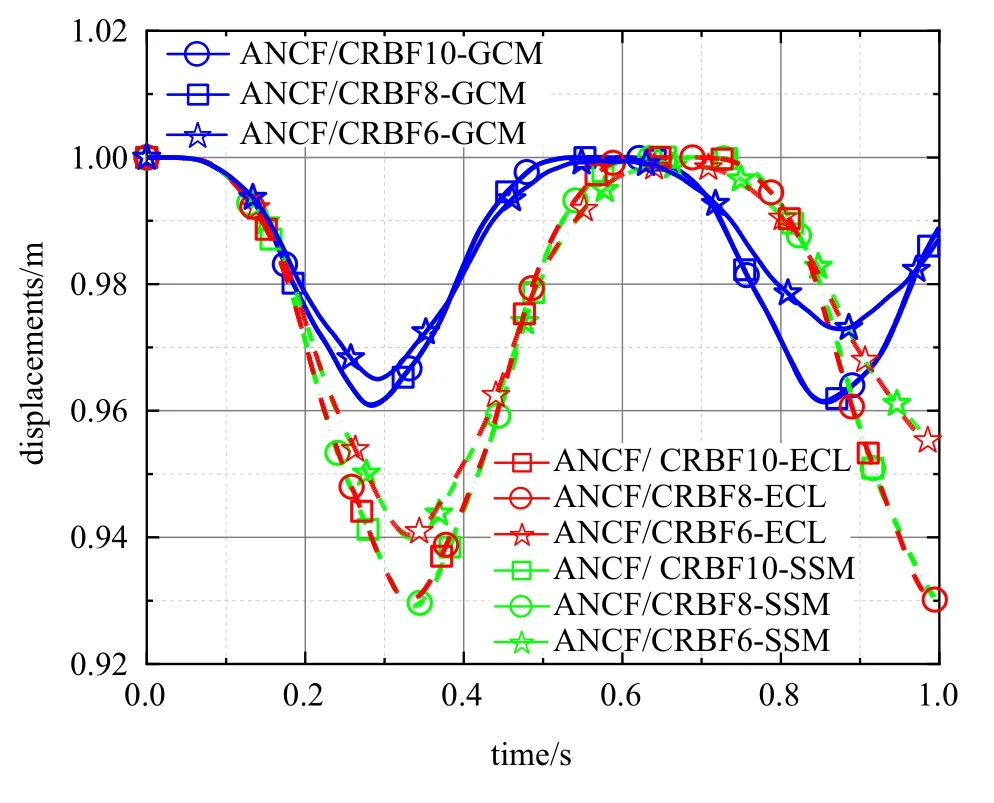
图9 梁端点处X 方向位移变化Fig.9 Tip horizontal displacement of the cantilever beam
4.5 动力学测试:柔性单摆算例
本小节采用经典的柔性单摆算例分析ANCF/CRBF10、ANCF/CRBF8 和ANCF/CRBF6 三种单元的动力学特性,如图10 所示.根据前面静力学分析的结论,本算例弹性力的计算采用应变分解方法.单摆的参数分别为长度l=1 m,高度和厚度h=w=0.02 m,弹性模量E=20 MPa,密度ρ=7200 kg/m3,以及泊松比ν=0.3.在重力作用下,单摆在XY平面内运动,仿真时间为2 s.采用20 个ANCF/CRBF 单元模拟.采用商业有限元软件LS-DYNA 中的Belytschko-Schwer beam(BS beam)单元作为对比[40],采用30 个BS beam单元模拟.另外,为最大程度上保证自编程序和有限元软件的一致性,均采用显式积分方法,这样可以避免采用隐式积分算法时的数值阻尼对计算结果的影响.此外,自编程序和有限元软件在截面方向的高斯积分点的选取均为3 个.

图10 柔性单摆模型Fig.10 Flexible pendulum

图11 梁端点处Y 方向位移变化Fig.11 Tip vertical displacement of the flexible pendulum
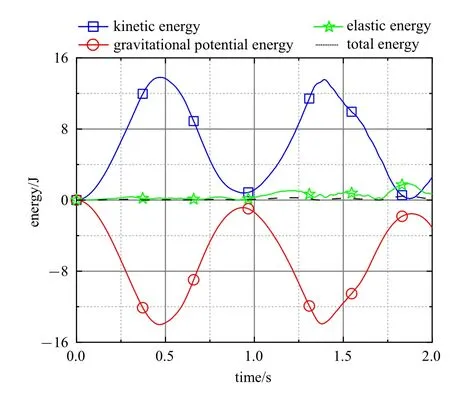
图12 ANCF/CRBF8 单元能量变化Fig.12 Energy change of ANCF/CRBF8 element
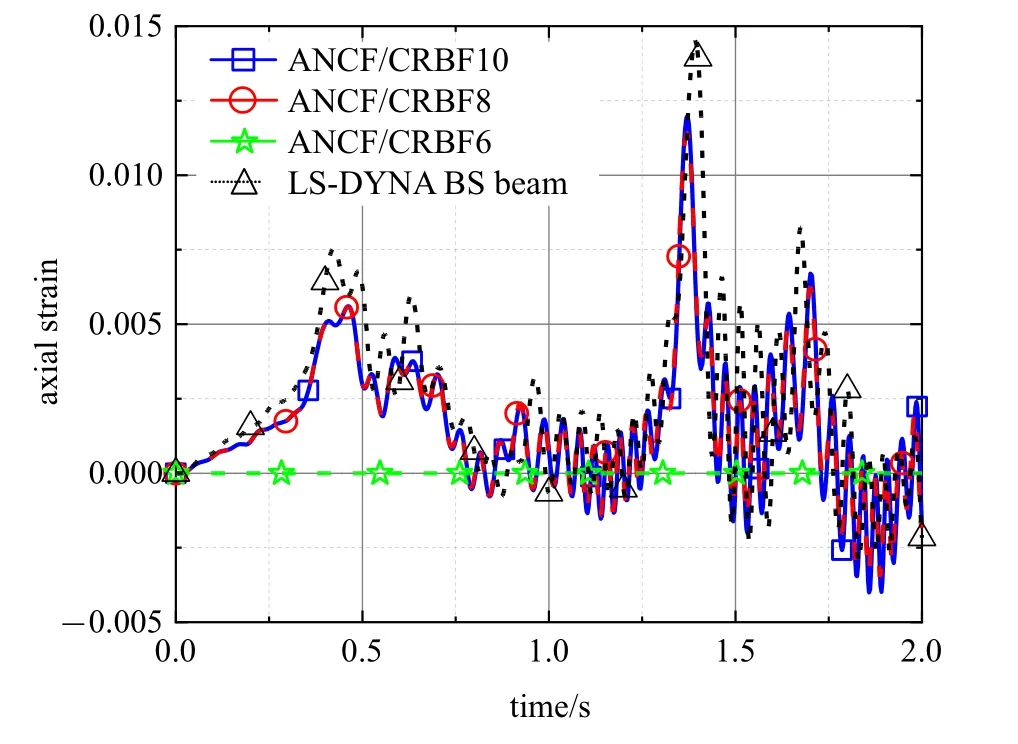
图13 梁中点轴向应变变化Fig.13 Axial strain change of beam middle point
图11 为梁末端端点处Y方向位移变化,可以看出ANCF/CRBF10 和ANCF/CRBF8 单元计算的结果与LS-DYNA 软件计算的结果有较好的吻合度,验证了单元在大范围刚体运动时可准确描述弹性变形的能力.而ANCF/CRBF6 单元由于轴向不能伸展,计算结果错误,不适用于模拟大变形梁问题.图12 是ANCF/CRBF8 单元的能量变化曲线.可以看出单元能量守恒,从能量的角度验证了模型的正确性.图13 是梁中心点处轴向应变变化情况.ANCF/CRBF10 单元和ANCF/CRBF8 单元轴向均可以伸展,数值变化较为吻合,而ANCF/CRBF6 单元完全约束了轴向变形,因此无轴向应变变化.另外可以发现LSDYNA BS beam 单元轴向应变与ANCF/CRBF梁单元轴向应变的变化趋势相同,但是幅值稍微偏大.这可以归因于四点:第一,LSDYNA BS beam 单元与ANCF/CRBF 梁单元采用了根本不同的位移场插值策略.ANCF/CRBF 梁单元选择对轴向和截面方向采用统一的插值策略,使得轴向、弯曲和剪切变形模态高度耦合,导致了系统刚度的上升,造成了轴向应变的减小.LSDYNA BS beam 单元基于共旋坐标法,对位移和转动采用了独立插值的策略,各个变形模态不会产生高度耦合现象,单元的系统刚度小于ANCF/CRBF 梁单元,所以轴向应变变化较大.第二,LSDYNA BS beam 单元与ANCF/CRBF 单元采用不同的坐标系统.由于ANCF/CRBF10 单元含有梯度向量以及ANCF/CRBF8 单元含有伸展系数,因此在进行边界转动副约束时也与LSDYNA BS beam 单元的边界约束条件不同.第三,LSDYNA BS beam 单元和ANCF/CRBF 单元的求解过程不同.LSDYNA 软件采用增量求解过程,而ANCF/CRBF 采用非增量求解过程.第四,两种模型采用的显示积分方法分别为MATLAB 和LSDYNA 软件自设的算法,在误差判断和步长选择上有所差异,随着模拟时间的延长,两种解之间的差异是可以预见的.
图14 是梁中心点处剪切应变变化情况.由于ANCF/CRBF8 单元和ANCF/CRBF6 单元节点处同时施加了轴向和截面方向的运动学约束,因此节点处不存在剪切变形.ANCF/CRBF10 单元仅约束了截面的变形,未约束截面与轴线的转动,因此节点处存在剪切效应.
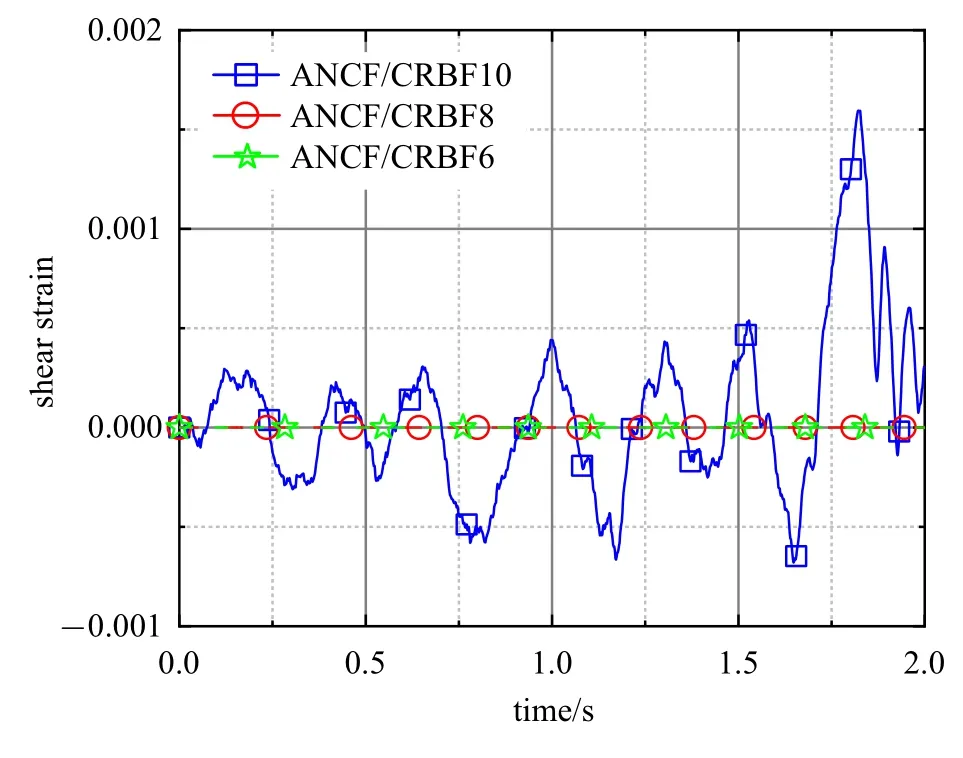
图14 梁中点剪切应变变化Fig.14 Shear strain change of beam middle point
相比传统ANCF/CRBF10 单元,本文构造的ANCF/CRBF8 和ANCF/CRBF6 单元的自由度更少,使得模型维度更低.例如,在柔性单摆算例中,ANCF/CRBF10,ANCF/CRBF8 和ANCF/CRBF6 单元建立的模型自由度分别为105,84 和63,仿真时间分别为139.2 min,121.3 min 和48.7 min(仿真环境为16 GB 内存,Intel Core i7 计算平台).此外,相比传统ANCF/CRBF10 单元,本文构造的ANCF/CRBF8 和ANCF/CRBF6 单元坐标没有梯度向量,可直接对其转角参数施加运动约束或力约束,便于面向旋转的设计操作.
汤惠颖等[46]基于李群SE(3)局部标架,研究了几类梁单元的闭锁缓解方法.文中分别采用Hu-Washizu 三场变分原理和应变分解法,缓解了SE(3)局部标架几何精确梁单元的剪切闭锁和绝对节点坐标梁单元的泊松闭锁,提升了单元的计算精度.对比本文与文献[46]可以发现:(1)文献[46]的特点是引入李群SE(3)局部标架,可消除刚体运动带来的几何非线性[47],极大地减少迭代矩阵的更新次数,有效地提升了计算效率;本文的特点是引入单元截面的运动约束,可消除截面处的泊松闭锁,缩减了单元的自由度,在低维动力学问题上提升了计算效率.(2)文献[46]与本文均采用应变分解法处理绝对节点坐标单元的泊松闭锁问题,在静力学和动力学问题上的计算精度均得到了较好地提升.
另外,汤惠颖等[46]发现高阶几何精确梁单元比低阶几何精确梁单元的计算精度高.这可启发本研究进一步拓展到绝对节点坐标高阶梁研究方面,例如三维三节点梁单元[48]和三维高阶梁单元[49-50].由于绝对节点坐标高阶梁没有闭锁问题,因此可结合本文的一致旋转场列式方法开发出精度较高的三维ANCF/CRBF 高阶梁单元.
5 结论
本文系统地研究了基于一致旋转场列式的绝对节点坐标平面梁单元的泊松闭锁问题.文中首先开发了两种刚性截面的绝对节点坐标平面梁单元ANCF/CRBF8 和ANCF/CRBF6,并对比了泊松闭锁问题在新单元与已有ANCF/CRBF10 梁单元上的特点.随后,结合两种闭锁缓解技术,弹性线方法和应变分解方法,研究了单元的收敛性.通过典型的静力学和动力学算例测试了泊松闭锁问题对ANCF/CRBF 单元性能的影响,可得到以下结论:
(1)对比ANCF 全参数梁单元,ANCF/CRBF 单元对节点梯度向量进行了约束,导致节点处不能完全捕捉泊松效应,但单元内部可以完全捕捉泊松效应,这种不连续情况会加重单元整体的泊松闭锁问题,极大地降低静力学计算精度.ANCF/CRBF 单元不具有静力学的计算优势,特别是在单元受集中力矩的强几何非线性情况.
(2)对比三种ANCF/CRBF 单元,对节点梯度向量约束的越多,导致计算深梁结构的静力学精度越差.对于长宽比较大的细长梁结构,梁的弯曲变形不会导致轴向伸展,刚性截面致使整体单元近似满足欧拉梁假设.
(3)在ANCF/CRBF 单元的基础上结合应变分解方法,可以更加有效地缓解单元泊松闭锁问题,动力学计算结果具有良好的精度,ANCF/CRBF 单元更适用于模拟动力学问题.

