探测器对超音速刚性盘−缝−带型降落伞系统的影响1)

龚升 吴锤结

(大连理工大学航空航天学院,辽宁大连 116024)

引言

火星是地球的近邻,其特征在很多方面与地球很相似,特别是美国的多项火星探测计划,使人类对火星有了更进一步的认识.探测结果表明:火星可能具有生命存在的某些必要条件,极有可能成为人类未来开发的理想星球,特别是2014 年林杨挺研究团队在对提森特(Tissint)火星陨石的研究中发现其碳颗粒来自火星生命产生的碳[1].而在火星探测任务中,柔性材质的降落伞系统具有良好的透气性、优良的气动减速性能以及体积小、质量轻等特点,使其成为了火星探测计划中气动减速器的首选[2].

由于火星大气密度较低且环境复杂,且距离火星较远,与探测器之间的信号交换传输存在着一定的延迟,对于火星探测器的降落以及着陆过程无法做到实时的控制,因此火星探测任务主要依靠降落伞系统作为气动减速器来使得探测器安全着陆于火星表面.通常火星探测降落伞系统的工作过程主要包括:自由降落阶段、伞绳拉直阶段、伞衣充气阶段以及稳定下降阶段,其工作环境在超音速以及低动压的状态.早期人们通过超音速风洞实验以及高空飞行空投试验等对降落伞系统的气动减速性能进行了研究,去重复设计了降落伞系统的尺寸大小等[3-6].近年来,人们开始采用各种数值计算模型来研究超音速降落伞系统流场流体结构特征,对各种类型的降落伞系统的拉直阶段过程以及伞衣充气阶段的最大拉直力、伞绳的抽打现象以及“绳帆”现象等进行了分析[7-13].结果表明:降落伞系统重要的伞衣充气阶段是一个复杂的时空变化过程,在较短的时间里,降落伞系统伞衣外形发生了剧烈的变化,柔性伞衣与周围非定常流体相互耦合、相互剧烈作用[14-17].在超音速流场中,降落伞系统伞衣内外流场都是显著的湍流流场,伞衣内部流体达到饱和状态后,流体将沿着伞衣壁面逆向运动溢出,其中从降落伞系统伞衣边缘、缝结构等溢出的一部分流体会引起伞衣边缘的剧烈振荡,这会使得伞衣出现折叠、坍塌等现象[18-19],以至于整个降落伞系统工作的失败,因此对超音速探测器−降落伞系统进行基础理论研究是航空航天领域的迫切需求.前人对降落伞系统与周围流场中的非定常激波、旋涡、湍流以及边界层等多物理相互作用过程中所导致伞衣不稳定振荡的原因缺乏了解[20-21].

前面研究了流体初始马赫数为2.0 时的探测器−刚性盘−缝−带型降落伞系统的气动减速性能以及流场结构特性.结果表明:探测器后端的湍流尾迹对降落伞系统伞前弓形激波以及伞衣内部的流场流体结构具有很大的影响,因此本文将进一步研究超音速下探测器的存在与否对刚性盘−缝−带型降落伞系统的气动减速性能以及流场流体结构特性的影响.为后续研究超音速探测器−柔性降落伞系统的流固耦合现象的数值模拟研究提供流场数据分析作用,以期找到影响降落伞系统伞衣流场不稳定现象的机理原因.

1 数值方法

1.1 流体控制方程以及湍流模型

本文研究的是探测器的存在与否对超音速刚性盘−缝−带型降落伞系统的气动减速性能以及流场流体结构特性的影响.对于三维非定常可压缩流体流动,因为在超音速流场中涉及到激波或接触不连续间断等情形,因此选择守恒积分形式的三维流体控制方程是很有必要的,这是捕捉求解间断不连续处的流体速度、压强等参量的关键.因此流体流动选择的是空间位置固定的极小有限控制体模型,通用的流体控制方程如下

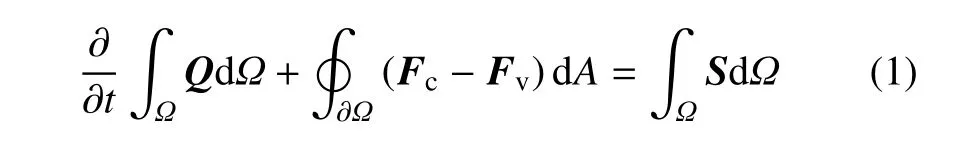
式中,Q,Fc,Fv分别表示为单位质量流体单元的守恒变量向量、对流矢通量以及黏性矢通量;源项S涉及到单位质量流体单元所受体积力和体积加热的作用[22-23].

为了精确模拟计算超音速火星探测器−刚性盘−缝−带型降落伞系统流场中的大尺度旋涡结构,存在着很多大涡模拟方法[24-26].本文采用了密度加权过滤方式的大涡模拟方法[27].对于密度加权过滤器(又称Favre 过滤器):是对流场中的流体密度、压强物理量采用简单的物理空间过滤,用上标“−”表示;对流场中的流体速度、温度以及内能物理量则采用密度加权过滤,并用上标“∼”表示,则有

采用密度加权过滤后的气体状态方程为

式中,T表示流体绝对温度.

对三维非定常可压缩流体的Navier-Stokes 方程进行Favre 过滤后,得到的微分形式的大涡数值模拟方程如下

过滤后的动量方程中产生了两个附加项,它们与亚格子脉动有关.而亚格子应力项

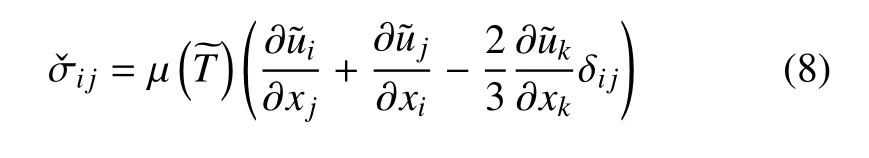
过滤后的可压缩流体的能量方程比较复杂,有更多的不封闭项.其中式(6)右端第一项为可解尺度分子应力做功,第二项为可解尺度导热项,而最后一项ˇA则包括6 项,需要附加的亚格子模式.对于亚格子模型的构造,采用的是Pullin 提出的拉伸涡亚格子模型(stretched-vortex sub-grid model)[28-30].

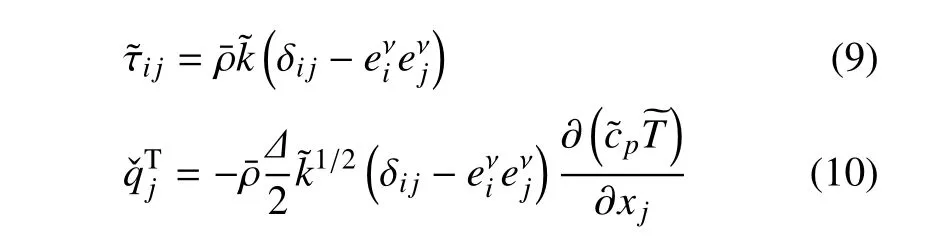
式中,eν为亚格子涡轴单元向量;为流体运动黏性系数;为亚格子湍流能量[31-33],其表达式为

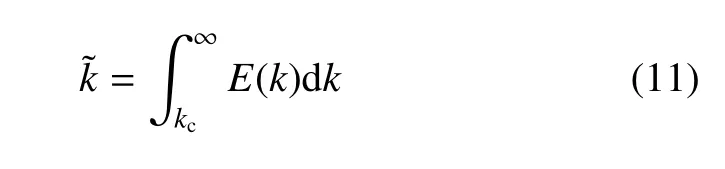
式中,kc为湍流流场最大可解波数,kc=π/∆.

对于刚性降落伞系统的气动阻力的计算,考虑到降落伞伞衣是不发生变形的,即降落伞系统的气动阻力D可以表示为

式中,Si为降落伞表面第i个三角形单元面积,∆qi为对应单元内外表面的压强差.

1.2 离散方法

本文采用有限体积法对流体控制方程进行离散:其中对流项采用的是混合形式的TCD-WENO 方法分别求解光滑流场以及激波间断区域[34-35],黏性项采用了二阶三点中心差分格式;时间项离散使用的是TVD (total variation diminishing)型强稳定性的三步三阶Runge-Kutta 法.根据流体压强和密度的相关曲率阈值来判断流场是否有激波的存在,来选择相应的计算格式.定义域为

2 模型建立

2.1 探测器−刚性盘−缝−带型降落伞系统模型

本文研究的是三维超音速探测器−刚性盘−缝−带型降落伞系统模型,其中探测器是海盗号(Viking-Type)类似形状:前端倾角为70◦,后端倾角为40◦.图1 所示为探测器−刚性降落伞系统的二维结构示意,其中流体沿X轴正向流动,探测器位于流场的上游,固定在图1 的左侧;而降落伞系统固定在图1 的右侧.以探测器最大截面形心处作为三维笛卡尔坐标系的原点,该点到降落伞系统带结构边缘的距离记为H,刚性降落伞系统带结构以及缝结构的宽度分别记为LB和LG.此外,降落伞系统伞衣厚度为5.0×10−4m,降落伞系统是通过多跟柔性伞绳连接固定在A点的吊绳上与探测器组成完整系统,该点距原点的距离记为L,由于悬挂伞绳的长度特征尺度与降落伞系统的长度特征尺度相比可忽略不计,故在数值模拟中将不考虑悬挂伞绳对探测器−刚性降落伞系统流场结构的影响.

图1 探测器−降落伞系统的二维结构示意图Fig.1 Configuration of 2D capsule/parachute system

如图2 所示,为探测器以及刚性盘−缝−带型降落伞系统的几何尺寸示意图.在图2(a)中探测器的最大截面直径记为d、宽度记为h;如图2(b)所示,为刚性盘−缝−带型降落伞系统,其几何外形为展开的圆形伞弧面状,公称直径记为Dp,盘结构顶端通气孔直径记为Dv.

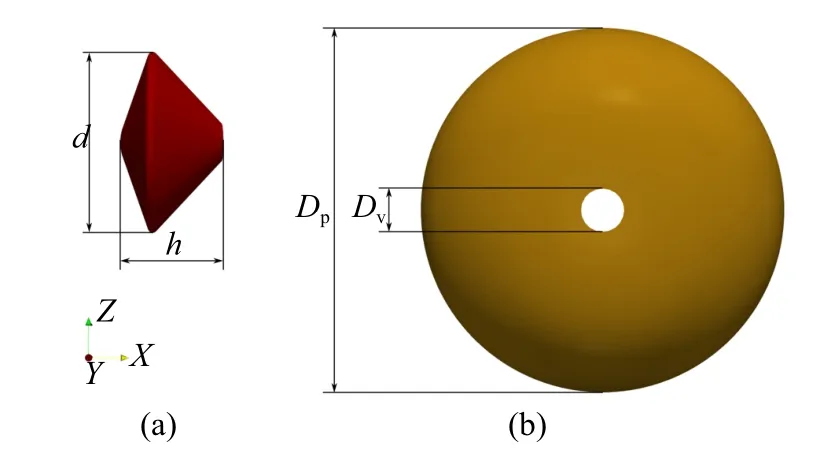
图2 探测器(a)以及降落伞系统(b)的尺寸Fig.2 Size of the capsule(a)and the parachute system(b)

探测器以及刚性盘−缝−带型降落伞系统模型参数尺寸,如表1 所示.

表1 探测器−降落伞系统模型尺寸参数Table 1 Size parameters of the capsule/parachute system model

2.2 网格划分以及参数设置

对于探测器−刚性降落伞系统来说，固体表面网格采用的是非结构类型的三角形单元表面网格,采用ICEMCFD 及Gmsh 软件联合进行生成.其中,探测器−降落伞系统网格节点总数为73 626,对应的三角形表面网格单元总数为146 064;而对于降落伞系统,其网格节点总数为38 048,三角形表面网格单元总数为74 912.探测器−刚性盘−缝−带型降落伞系统的表面网格,如图3 所示.

在数值模拟算例中,三维的流场计算域范围为:[−0.5,2.5]×[−0.75,0.75]×[−0.75,0.75](m),流场区域网格采用了Berger-Oliger 类型的多层块结构自适应网格加密技术,与非结构自适应策略最大的不同在于多层块结构自适应加密网格在稠密网格上同时加密了时间步长,且各层网格之间的加密因子f=2,流体的动力黏性系数µ=5.325 2×10−5kg/(m·s).为了更好地与前人的数值模拟结果进行对比分析,本数值模拟采用Barnhardt 等[21]的数值模拟流场参数,如表2 所示.

数值模拟的初始边界条件为:在流体主流动方向上的上游边界为流动进口边界,设置了流体的初始密度ρ∞=0.219 9 kg/m3、初始压强q∞=10 914.1 Pa以及初始马赫数Ma=2.0;计算区域的其他边界均为流体流动出口边界,即流体流动是充分发展状态的;在探测器以及刚性降落伞系统的固体壁面上,则设置为无滑移边界条件,即壁面上的流体速度分布为零.

探测器−刚性降落伞系统流场流体雷诺数(Re)可以表示为

式中,d为探测器最大截面处直径.

如图4 所示,为流体初始马赫数大小为2.0 时,沿主流动方向上的探测器−刚性降落伞系统流体马赫数大小分布切面示意图.其中上图为Graham[21]数值模拟结果;而下图为本文数值模拟结果.对比两图可以发现,在超音速流场中,探测器−刚性降落伞系统的流场结构大致是吻合的,探测器以及降落伞系统伞前弓形激波都较为明显,探测器后端的低速湍流尾迹都与伞前激波相互作用;另外,当伞衣内部流体饱和后,逆向运动的流体也与伞前激波相互作用,这使得激波结构与位置都发生了改变.在本数值模拟中,可以发现,刚性盘−缝−带型降落伞系统流场流体结构更为细致,在伞衣内部,低马赫数流体区域范围更大,从伞衣内部溢出的流体与伞前激波相互作用,形成了明显的膨胀波并与伞前激波相互融合,且在伞衣后端的复杂湍流尾迹区域,流场湍流混合得更为充分.

3 结果与分析

3.1 探测器对降落伞系统的气动减速性能影响

本节中将研究讨论探测器的存在与否对刚性盘−缝−带型降落伞系统的气动减速性能的影响.首先,前面研究了不同自适应加密网格分辨率对刚性盘−缝−带型降落伞系统气动减速性能以及流场流体结构特性的影响,并验证了自适应加密网格的收敛性[36].

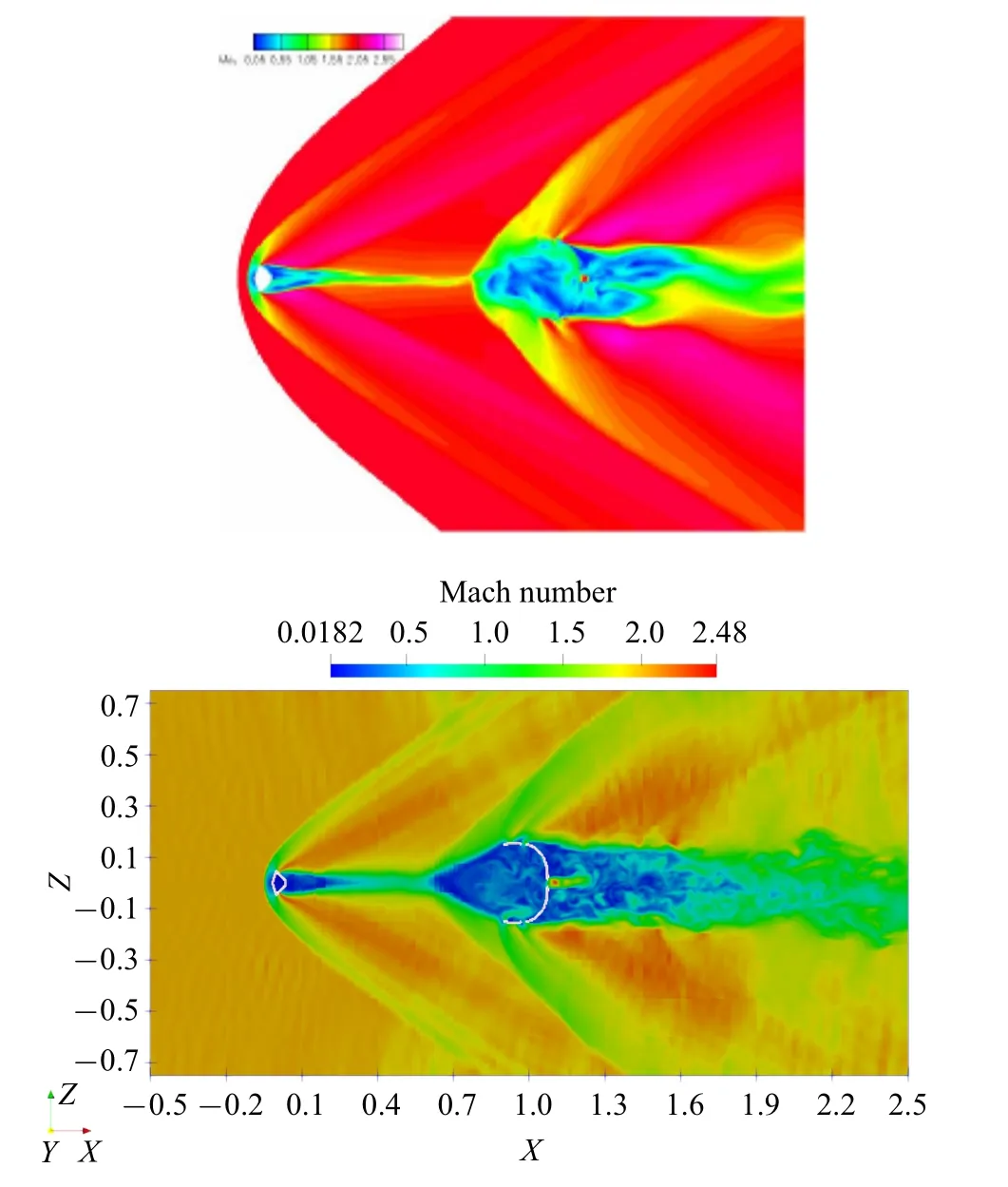
图4 超音速−降落伞系统流体马赫数大小分布切面示意图:上图为Graham 模拟结结果[21],下图为本算例数值模拟结果Fig.4 Two-dimensional composite rendering of Mach number of the capsule/parachute system:upper panel is Graham’s result,lower panel is the simulation of our case

本文中流场采用的是Berger-Oliger 类型三层块结构自适应加密网格,如图5 所示.其中图5(a)为自适应网格沿主流动方向上的二维切面视图;而图5(b)对应的是该时刻自适应网格的三维视图.可以观察到,此时在探测器前端激波区域、后端的尾迹区域、伞衣前端弓形激波区域以及后端复杂的尾迹区域的网格都进行了较为充分的网格加密,三层块结构自适应加密网格可以保证网格单元内的流体物理量的计算精度,同时较大程度地降低了流场网格总量,节约了并行计算集群计算载荷以及计算时间等.

第一步，将一棵三角枫树先在D处横锯，再从横截面里口的F点向下锯到G点（C线）；第二步，在树下部E处横锯，再在横截面里口向上锯到H线。一年以后，C线以上（包括A段）都活得很好，伤口也在向愈合的方向发展。几次实验结果完全一样。

采用32 核数(8*AMD,CPU Opteron 8350 四核、主频2.0 GHz)的并行计算集群进行数值模拟.其中探测器−刚性降落伞系统计算分配的核数为2,而非定常可压缩流体的数值模拟分配的核数为30.数值模拟初始时间步长为1.0 × 10−5s,随着计算时间的推进,随后的时间步长量级均为10−6s,为了满足数值模拟过程中的稳定性以及收敛性条件,最大的CFL(Courant-Friedrichs-Lewy,CFL)数为0.95,当CFL 数大小超过0.98 时,数值模拟将自动调整时间步长重新进行计算,而允许的最大时间步长为1.0×10−4s,数值模拟总时间为200.0 ms,输出结果数为400.

图5 三层块结构自适应加密网格Fig.5 Three-layer block-structured adaptive refinement grids

对于探测器−降落伞系统的数值模拟,自适应基础网格数为160 × 80 × 80,当数值模拟计算时间T=113.0 ms 时,动态的自适应网格总数量级约为4.8×106,并行计算总时间为9.28 d.如图6 所示,为流体初始马赫数为2.0 时,探测器−刚性降落伞系统气动阻力随计算时间的变化示意图.可以发现,在数值模拟初始阶段,此时的流体还处于不充分发展状态,降落伞系统的气动阻力出现了剧烈的振荡,其所受气动阻力最大载荷为6919.74 N,一般在经过10 倍的流动时间t(定义为探测器−降落伞系统的拖尾距离H与流体初始速度u∞之间的比值)后,对应的计算时间T为

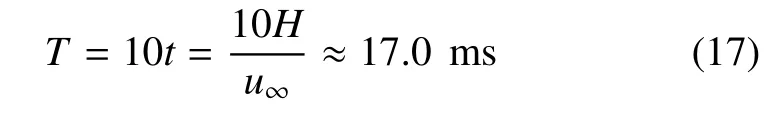
即,经过计算时间T=17.0 ms 后,流体过渡到了充分发展状态,降落伞系统的气动阻力大小振荡幅值趋于平稳.降落伞系统的气动阻力系数CD的通用表达式为

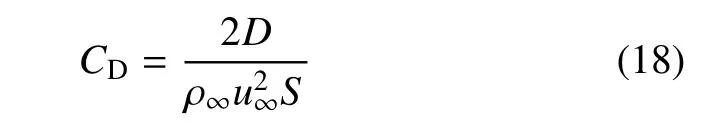
式中,D为降落伞系统的气动阻力,S为降落伞伞衣名义面积.

图6 Ma=2.0 时的探测器−降落伞系统的气动阻力变化Fig.6 Variation in aerodynamic drag of the capsule/parachute system at Ma=2.0

当探测器−降落伞系统流体逐渐过渡到充分发展状态以后,探测器−降落伞系统时间平均的气动阻力为1194.32 N,其对应的标准差为242.65 N,气动阻力振荡脉动占时间平均气动阻力的20.32%,探测器−降落伞系统时间平均的气动阻力系数CD为0.525.结果表明:探测器后端的湍流尾迹运动与伞衣前端弓形激波相互作用;另外,降落伞系统伞衣内部因饱和而逆向运动溢出的流体也与伞前激波相互作用,这使得伞前激波的形状以及位置发生了改变,且伞衣内部流体难以达到稳定状态,这就加剧了降落伞系统的气动阻力的振荡脉动.

如图7 所示,为有无探测器且流体初始马赫数为2.0 时,降落伞系统气动阻力变化对比示意图.在无探测器时,流场采用的三层块结构自适应加密网格相应计算时间上的总数量级约为2.8×106,对应的并行计算总时间为3.48 d.此时的降落伞系统气动阻力变化与有探测器时是一致的,在数值模拟的初期出现了剧烈的振荡,降落伞系统所受气动阻力最大载荷为6511.82 N.为了能更为细致地对比分析探测器对降落伞系统气动减速性能的影响,图7 中所示的是计算时间T=4 ms 之后,降落伞系统气动阻力变化对比.可以观察到,在无探测器时,降落伞系统的气动阻力的整体数值较高,降落伞系统时间平均的气动阻力达到了3704.19 N,是有探测器时间平均的气动阻力1194.32 N 的3.10 倍;而无探测器时,降落伞系统气动阻力变化标准差只占时间平均气动阻力的0.50%;相应的有探测器时,该气动阻力变化标准差占比为20.32%,增大幅度达到了40.64 倍.

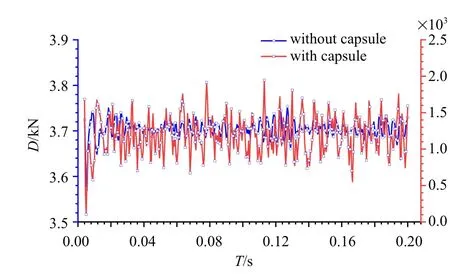
图7 有无探测器时的降落伞系统气动阻力变化对比Fig.7 Comparison of aerodynamic drag of the parachute system with/without the capsule

因此可以得出以下结论:在无探测器时,刚性盘−缝−带型降落伞系统流场中激波、湍流以及分离流等多物理相互作用强度较弱,流场处于较为稳定的状态,扰动较小;而有探测器时,探测器后端的湍流尾迹运动发展与伞衣前端弓形激波相互作用以及伞衣内部逆向运动溢出的流体之间的周期性相互作用,使得伞前弓形激波结构位置和形状发生了改变,伞衣内部流体很不稳定,表现出了周期性变化的特点.这对刚性盘−缝−带型降落伞系统的气动阻力大小和振荡脉动都有较大的影响.在流体初始马赫数为2.0 时,探测器的存在与否对刚性盘−缝−带型降落伞系统气动减速性能的影响,如表3 所示.降落伞系统所受气动阻力最大载荷记为Fmax、降落伞系统时间平均的气动阻力记为Da、气动阻力振荡脉动占比为δ 以及降落伞系统时间平均的气动阻力系数记为CD.

表3 探测器对降落伞系统气动性能的影响Table 3 Influence of capsule on aerodynamic performances of the parachute system

3.2 探测器对降落伞系统的流场流体结构特性影响

本节研究探测器对刚性盘−缝−带型降落伞系统流场流体结构特性的影响.如图8 所示,流体初始马赫数为2.0 且计算时间T=127.0 ms 时,降落伞系统流体马赫数大小分布切面以及等值线示意图.其中,如图8(a)所示,为无探测器时情形,可以观察到,此时流体过渡到了充分发展状态,在伞衣前端形成了稳定光滑的弓形激波结构,而伞衣内部的流体马赫数较低,流场稳定、扰动较小.从伞衣盘结构顶端通气孔流过的流体还保持着超音速的状态,该区域的流体马赫数最高,大小为3.59.另外,从伞衣边缘溢出的流体,沿着伞衣壁面运动进入伞衣后端的湍流尾迹区域,此时的尾迹流场湍流扰动较小,且流体马赫数较低.

图8 T=127.0 ms 时的降落伞系统流体马赫数分布切面以及等值线示意图Fig.8 Schematic slide and contour rendering of Mach number of the parachute system at T=127.0 ms

如图8(b)所示,有探测器时,降落伞系统流场流体结构细节更加丰富.其中,在探测器前端形成了弓形激波结构,其后端是一个明显的流体低马赫数的湍流尾迹区,尾迹区的流体运动发展与伞衣前端激波相互作用,形成了马赫数较大的膨胀波,并且使得伞前激波区域的位置和范围都发生了改变,当伞衣内部流体达到饱和状态后将不断逆向溢出与伞前激波相互作用,这使得伞衣内部流体运动极不稳定,形成了周期性的充气饱和、饱和后溢出以及随后继续充气饱和的循环类似“呼吸运动”.另外,部分流体从伞衣带结构边缘、缝结构以及顶端通气孔溢出形成脱落的旋涡结构,进入伞衣后端的湍流尾迹区域.因为伞衣内部流场的不稳定,使得伞衣后端的尾迹区域也不稳定,尾迹区流场是一个旋涡、湍流以及分离流等多物理相互作用的流场,流体流动紊乱,大尺度旋涡结构运动分解成小尺度旋涡结构耗散了流场流体的动能,使得流场流体的速度降低,相应的形成了流体低马赫数区,且扰动较大,流场出现了摆动的现象.

图9(b)所示的是有探测器时,可以观察到,流体压强最大值出现在探测器的前端,由于探测器的存在,探测器的后端尾迹与伞前弓形激波相互作用,随后流场流体的压强增大.与无探测器伞衣内部流场相比,此时伞衣内部不再是高压强区,流体进入伞衣内部达到饱和状态后,伞衣内部的流体逐渐沿着带结构边缘、缝结构以及盘结构顶端通气孔等往外溢出,在图9(b)中的伞衣带边缘上下端都出现了流体压强的峰值,随着伞衣边缘脱落的旋涡结构进入到伞衣后端的尾迹区域,该尾迹区的压强大小分布是较小的.结果表明:探测器对于刚性盘−缝−带型降落伞系统的流场结构的影响,主要是由于探测器的存在,其后端形成的湍流尾迹向下游发展,破坏了降落伞系统伞前弓形激波以及伞衣内部流场的平衡状态,随之产生了大量的旋涡、湍流等结构,使得流场扰动增大.

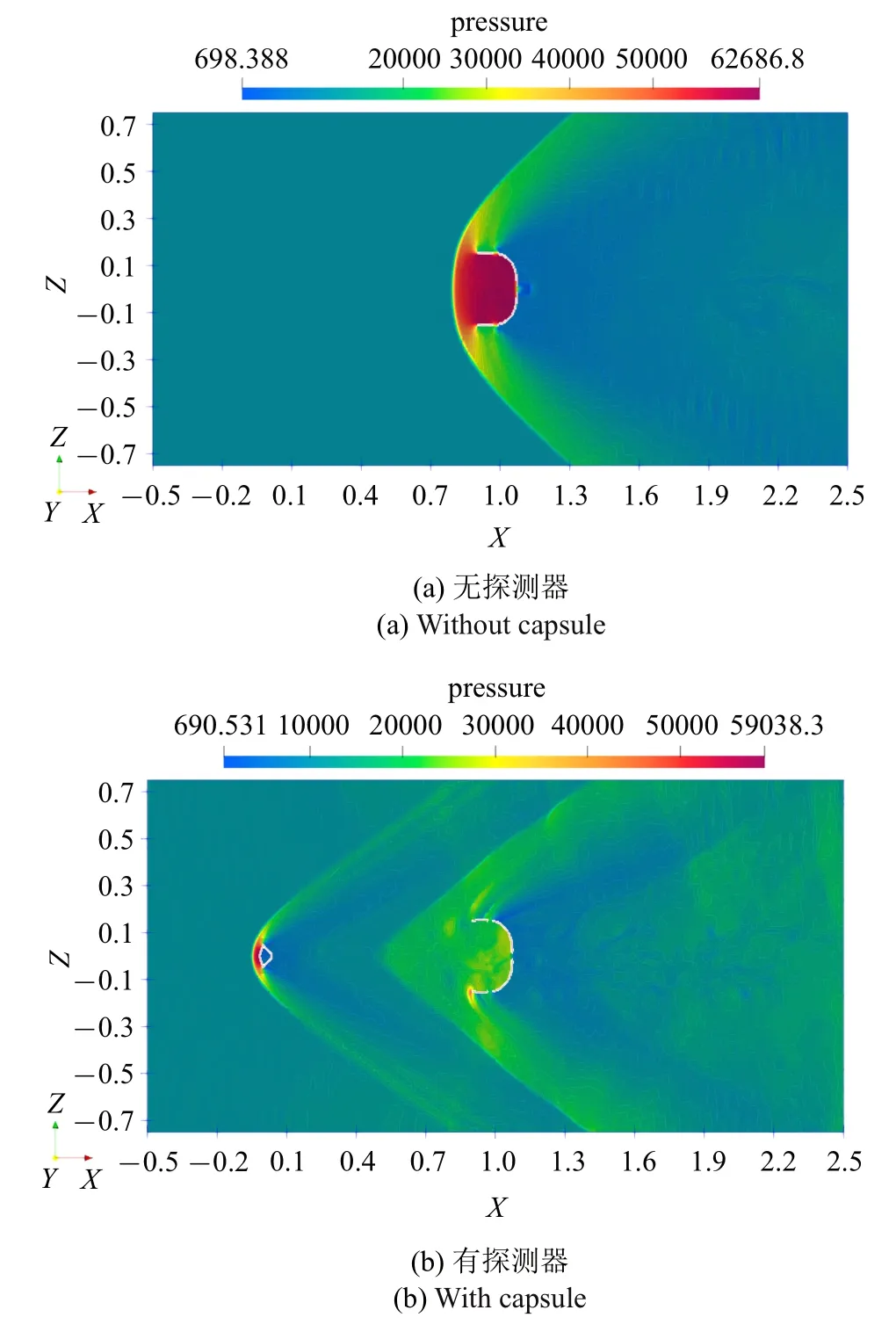
图9 T=127.0 ms 时的降落伞系统流体压强分布切面以及等值线示意图Fig.9 Schematic slide and contour rendering of pressure of the parachute system at T=127.0 ms

为了进一步研究探测器对刚性盘−缝−带型降落伞系统的流场流体结构的影响.如图10 所示,当计算时间T=127.0 ms 时,降落伞系统流体速度分量u的大小分布切面以及等值线示意图.其中图10(a)表示无探测器情形,流体速度分量u的分布与图8(a)所示的流体马赫数分布是相一致的,在降落伞系统伞衣前端也形成了稳定的激波结构,流体通过激波进入伞衣内部后,流体速度分量u有所降低,此时伞衣内部流场达到了饱和状态,流体速度分量u趋近于零.此外,从伞衣边缘溢出的流体进入伞衣后端的湍流尾迹区域,在尾流的近场区域沿Z轴上下两端的流体速度分量u为负值,表明该区域流体将沿着X轴负向运动,而从伞衣顶端通气孔流过的流体还保持着超音速正向流动的状态,该部分流体将与周围逆向流动的流体相互作用,形成类似的回流区;在图10(b)中,刚性盘−缝−带型降落伞系统伞衣内部流体以及伞衣后端的尾迹区域流体结构变化是巨大的,伞衣内部流场不再是稳定的,而是一个复杂的旋涡、湍流等多物理相互耦合时变的流场,该流场流体周期性的进入、溢出、再进入,使得流体混合得更充分,并形成了存在大量旋涡结构的回流区.

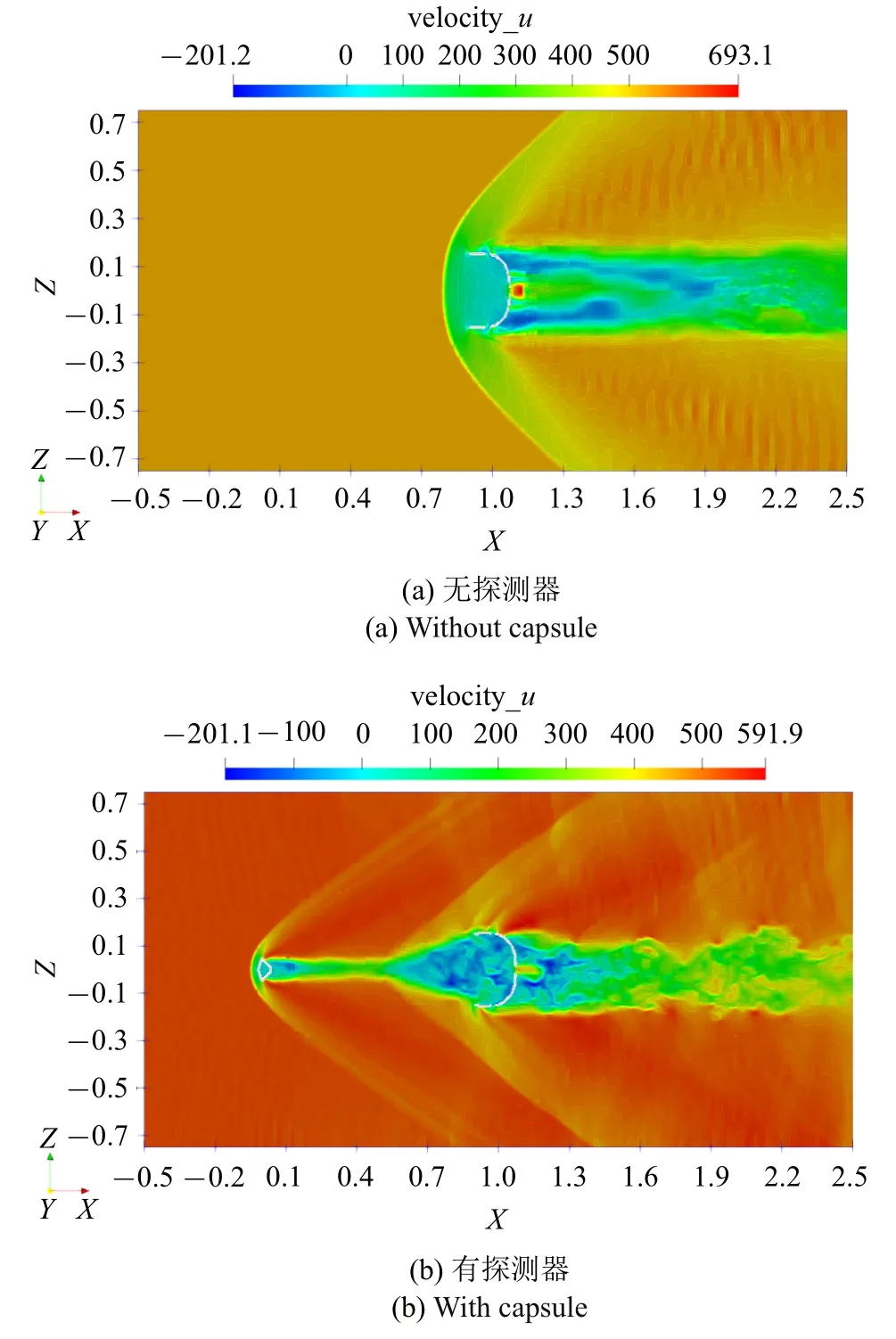
图10 T=127.0 ms 时的降落伞系统流体速度分量u 的大小分布切面以及等值线示意图Fig.10 Schematic slide and contour rendering of velocity u of the parachute system at T=127.0 ms

如图11 所示,为降落伞系统流体速度分量v的大小分布切面以及等值线示意图.其中,图11(a)为无探测器时情形.可以看到,此时在伞衣内部以及伞衣后端的尾迹区域,流体速度分量v的大小是较低的,且扰动小.当流体充分混合作用后运动发展到下游远场区域,此时正向运动与负向运动的流体相互耦合,存在着大量的旋涡结构,此时流体速度分量v的最大值为149.8 m/s;而在图11(b)中,伞衣内部流体速度分量v的大小分布很明显,当探测器存在时,伞衣内部流体是不稳定的,沿主流动方向运动的流体达到饱和状态后将沿着伞衣壁面方向运动,使得伞衣内部流体速度分量v增大,同时在伞衣后端的湍流尾流区域,正向和逆向运动的流体相互混合作用伴随着流体运动的始终,这就造成了该区域的流体流速变化较大,这与探测器−刚性盘−缝−带型降落伞系统的气动阻力大小变化的振荡脉动幅值较大是一致的.

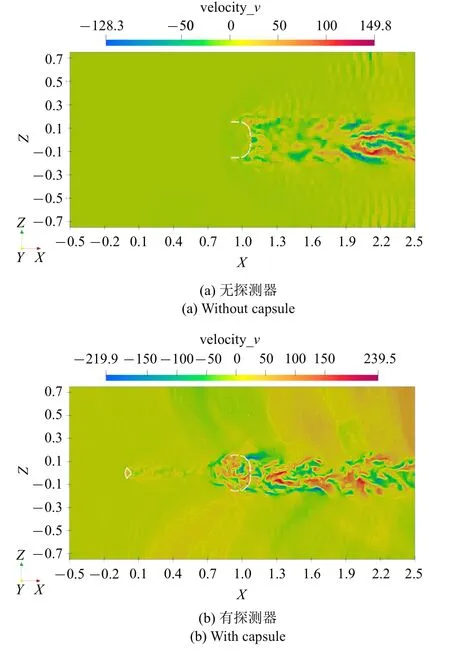
图11 T=127.0 ms 时降落伞系统流体速度分量v 的大小分布切面以及等值线示意图Fig.11 Schematic slide and contour rendering of velocity v of the parachute system at T=127.0 ms

图12 所示为降落伞系统流体速度分量w的大小分布切面以及等值线示意.从图12(a)可以看出,无探测器时,沿着横向Z轴方向上的流体速度分量w的大小分布.可以观察到,伞衣前端弓形激波区域是沿着Z轴正负两方向对称分布的,此时在伞衣带结构边缘以及缝结构处的流体速度分量w的值相对较大,最大值达到442.1 m/s;而伞衣后端的湍流尾迹区域,此时流场流体速度分量w大小变化较低,流场中旋涡、湍流等之间的相互作用影响变弱.相应在图12(b)中展示的是有探测器时,流体速度分量w的大小分布示意,在伞衣后端尾迹区至远场区域流体其变化与速度分量v的大小分布类似,此时尾迹区流体结构更加复杂,旋涡、湍流以及分离流等多物理相互耦合作用增强,使得该区域的湍流度增加,湍流运动耗散了流体动能,相应的流体压强也降低了.

图12 T=127.0 ms 时降落伞系统流体速度分量w 的大小分布切面以及等值线示意图Fig.12 Schematic slide and contour rendering of velocity w of the parachute system at T=127.0 ms

如图13 所示,当计算时间T=127.0 ms 时,刚性盘−缝−带型降落伞系统表面单元所受到的压力大小分布示意图.其中图13(a)为无探测器时情形,可以看到,此时在降落伞系统的带结构边缘大部分区域所受的压力较小,只是在局部区域出现了较高压力分布的情形,而在伞衣盘结构边缘以及顶端通气孔附近区域同样所受到的压力也较小,而在盘结构边缘到顶端通气孔之间部分则是高压力区.这是由于无探测器时,流体直接进入伞衣内部而达到饱和平衡的状态,使得伞衣内部的压力达到峰值,最大值可达59 374.4 Pa.从伞衣带结构、缝结构以及伞衣顶端通气孔稳定溢出的流体,使得这些区域附近的流体压强有所降低,相应的伞衣所受的流体压力大小也降低.图13(b)为存在探测器时的情形,此时在探测器前端表面单元受到的压力是最大的,与无探测器时的伞衣表面单元所受压力分布不同,在伞衣内部表面所受压力值明显降低,而只是在盘结构的局部边缘出现了压力较大区域,这与实际应用的超音速降落伞系统出现的伞衣边缘振荡、褶皱现象是一致的.结果表明:探测器对降落伞系统表面单元所受的压力分布很重要.当存在探测器时,可以很好地降低降落伞系统表面单元所受的流体压力作用,这对于降低降落伞系统的伞衣材料疲劳破坏至关重要,同时可以减缓降落伞系统的剧烈大变形运动,使得降落伞系统稳定性增强.

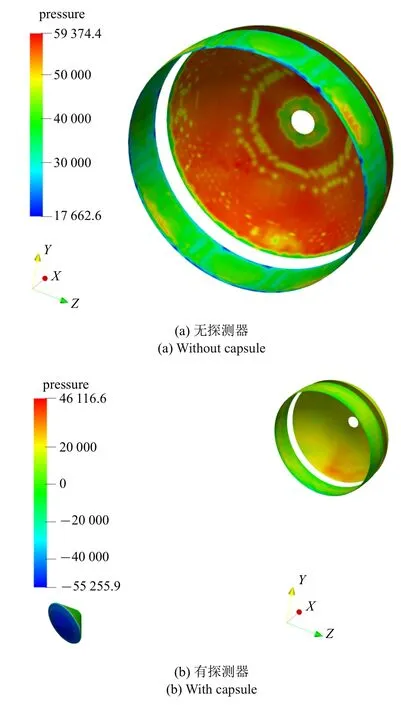
图13 T=127.0 ms 时降落伞系统表面单元所受压力分布示意图Fig.13 Schematic of surface pressure of the parachute system at T=127.0 ms

4 结论

本文对流场流体初始马赫数为2.0 时,探测器的存在与否对刚性盘−缝−带型降落伞系统的气动减速性能以及流场流体结构特性的影响进行了数值模拟研究.采用了兼顾强激波和大尺度湍流旋涡情形的混合形式的TCD-WENO 数值格式以及基于拉伸涡亚格子模型的大涡模拟方法,配合流场区域的多层块结构自适应网格加密技术.结果表明:在无探测器时,降落伞系统的流场结构稳定,扰动较小;而有探测器存在时,探测器后端的复杂湍流尾迹运动、伞衣内部逆向运动溢出的流体与伞衣前端弓形激波周期性的相互作用,使得伞前激波位置发生前移、激波倾角变小,且伞衣内部流场极不稳定.伞衣内部溢出的流体在伞衣边缘脱落形成旋涡结构,与降落伞系统伞衣后端的湍流以及分离流等相互作用,造成了尾迹区高度紊乱,加剧了降落伞系统的气动阻力振荡脉动变化,从而降低了降落伞系统气动阻力系数,同时使得降落伞系统尾迹流场流体结构更加复杂.这为后续考虑柔性伞衣的变形与超音速流体相互耦合作用,研究探测器对柔性降落伞系统的气动减速性能以及流场结构特性提供数据支撑.