随机参数系统不确定性量化的泛函观点与整体灵敏度分析1)
万志强 陈建兵,2) Michael Beer
∗(同济大学土木工程防灾国家重点实验室,上海 200092)
+(同济大学土木工程学院,上海 200092)
∗∗(莱布尼茨汉诺威大学风险与可靠性研究所,德国汉诺威30167)
引言
现代化土木工程建设正逐步走向整体化、精细化及全概率化的全新分析与设计范式.与之相应的是,数值仿真计算模型已然成为工程结构系统设计与分析中不可或缺的一部分.然而,设计与分析过程中不可避免地会遇到诸多不确定性因素的影响,如仿真计算模型的边界约束可能具有不确定性、初始条件可能难以精确给定、系统的某些力学性能参数可能具有不可忽略的随机性等[1-2].一般而言,这些不确定性因素均可表征为某种参数化的形式,如混凝土材料的抗压强度与弹性模量[3]、岩土材料的有效黏聚力与有效内摩擦角[4]、随机风场模型的地面粗糙度与剪切速度[5]等.
由于系统输入参数存在不确定性,必然导致系统输出亦存在一定程度的不确定性,因而仿真预测的结果不可避免地与实际情况存在一定偏离.研究表明,不同系统输入参数对系统输出不确定性的“贡献”一般是不同的.因此,量化系统输入参数对系统输出不确定性的影响(或称量化系统输出关于系统输入参数的灵敏度),即灵敏度分析,对工程设计、优化与决策具有重要意义[6].
灵敏度分析的目标是量化系统输入参数对系统输出不确定性的影响,即选择并计算灵敏度指标.例如,基于差商的基本效应指标[7](亦称为Morris 指标)及基于导数的灵敏度指标[8],主要适用于确定性系统,在本质上属于局部灵敏度的范畴.另一方面,针对随机参数系统,人们发展了基于方差分解的Sobol’指标[9]以及基于条件概率密度函数的矩独立指标[10]等整体灵敏度指标.这些指标侧重于对灵敏度“大小”的计算,因而往往其值恒为非负.这容易使人产生输入变量的不确定性总是使得输出变量的不确定性增大的错觉[11].事实上,系统输入参数对输出不确定性的影响是有“方向”的,而这一“方向”对结构分析、特别是考虑不确定性影响下的结构优化设计至关重要[12].例如,基于失效概率的灵敏度指标便是一类能同时反映灵敏度“大小”与“方向”的指标[13-14],被广泛用于基于可靠度的结构优化与设计之中[12-15].
在上述研究工作的基础上,Chen 等[16]提出了一类全新的基于Fr´echet 导数的整体灵敏度指标,并给出了相应的高效算法.其中,随机系统中不确定性传播的泛函观点虽已初具雏形,但尚未得以深入论述.同时,如何针对具体的工程问题采用基于Fr´echet 导数的整体灵敏度指标,特别是对参数进行灵敏度排序等相关问题的研究尚不够充分.
基于此,本文从随机系统中不确定性传播的泛函表达角度,进一步探讨了该整体灵敏度指标的数学定义、物理意义和基本性质.进而,在ε−等效分布的定义下,讨论了该整体灵敏度指标的参数化表达形式,给出了其对应的重要性测度和方向灵敏度的定义及其物理意义.建立了该整体灵敏度指标与矩独立指标之间的内在联系.结合概率密度演化−概率测度变换方法[17],提出了该整体灵敏度指标及其对应的重要性测度与方向灵敏度的数值计算方法和流程.最后,通过4 则算例分析详细讨论了该灵敏度指标的工程实用性.
1 随机系统中不确定性量化与传播的泛函观点
1.1 随机变量变换的泛函空间观点
在概率论框架下,随机系统中输入变量的不确定性可以随机变量(向量)的数学形式进行表征[18-19].记概率空间为(Ω,F,),其中Ω 为样本空间、F 为σ-代数(Ω 的事件域)、为概率测度,ϖ ∈Ω 代表样本空间中的一个点(即基本事件).不失一般性,考虑一随机系统

其中,g(·):Rn→Rm为一连续映射,其分量为(g1,g2,···,gm)T;Θ(ϖ)=(Θ1(ϖ),Θ2(ϖ),···,Θn(ϖ))T为n维输入随机向量,其联合概率密度函数pΘ(θ)已知,其中θ=(θ1,θ2,···,θn)T为随机向量Θ的可实现值;X(ϖ)=(X1(ϖ),X2(ϖ),···,Xm(ϖ))T为m维系统输出向量,记其联合概率密度函数为pX(x),其中x=(x1,x2,···,xm)T为随机向量X的可实现值.
由概率论可知,若已知pΘ(θ),则根据上式可确定输出随机向量的概率密度函数pX(x).事实上,根据概率守恒原理[20-21],可得
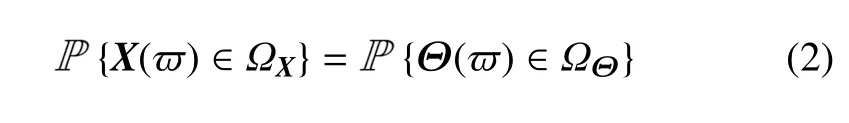
其中ΩΘ为输入随机向量值域空间的任意子域,ΩX为由式(1)中的映射决定的在输出随机向量值域空间中与ΩΘ对应的子域.由此可得

为简单计,先考察n=m=1 的情况.此时,式(1)成为标量形式X(ϖ)=g(Θ(ϖ)),而式(3)则相应地退化为∫ΩX pX(x)dx=∫ΩΘpΘ(θ)dθ.注意此时积分区域为ΩX=g(ΩΘ).进一步,考虑下列情况.(1)函数g(·)为单调函数.此时,有
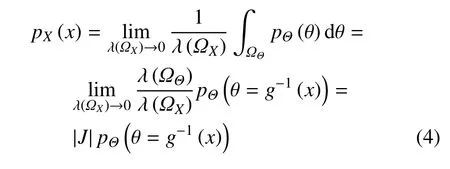
其中λ(·)表示子域的Lebesgue 测度,对一维情况即为其子域的长度;为Jacobi 行列式,对一维情况即为其导数之绝对值,g−1(·)表示g(·)的反函数.
(2)函数g(·)为非单调函数.此时,总可以将其定义域剖分为若干个不相交子域,并使之在每个子域中为单调函数[21].记其相应的反函数为(·)(j=1,2,···,N),N为子域划分段数,此时有

对其进一步化简可得

另一方面,也可以通过Dirac 函数δD[·]的筛选性质体现的映射关系获得输出变量的概率密度函数.事实上,对于上述情形,有
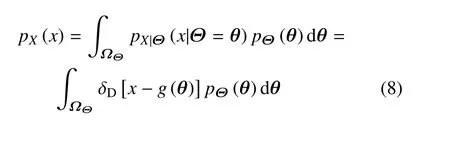
其中pX|Θ(x|Θ=θ)为条件概率密度函数.由于存在映射关系X(ϖ)=g(Θ(ϖ)),因而有pX|Θ(x|Θ=θ)=δD[x−g(θ)],由此可得式(8)中的第二个等式.
显然,可认为式(8)是输出概率密度函数pX(x)关于输入概率密度函数pΘ(θ)的隐式表达,而式(4)、式(5)和式(7)则是对式(8)进行积分获得的显式解析表达.上述各式表明,输出概率密度函数pX(x)由输入概率密度函数pΘ(θ)所决定,因而可以进一步写成如下算子形式的表达

其中下标g用来表示算子ψg决定于函数g(·).在实际工程中,函数g(·)描述了问题的物理机制,因此,式(9)表明:不确定性在系统中的传播,即从输入概率信息到输出概率信息的变换,是由系统物理机制所决定的.从函数空间来看,这一变换的实现是通过由物理机制决定的算子作用来实现的.
对于m≥2 的情况,上述基本思想是完全类似的.限于篇幅,兹不赘述.
1.2 随机动力系统中不确定性传播的泛函空间观点
这一泛函空间观点,对于随机动力系统中的不确定性传播也是适用的.为了明确起见,考虑如下随机动力系统[21]

其中X=(X1,X2,···,Xm)T为状态向量,˙X=∂X/∂t;G=(G1,G2,···,Gm)T为确定性函数向量;Θ=(Θ1,Θ2,···,Θn)T为刻画随机源信息的随机向量,其概率密度函数pΘ(θ)已知,这里θ=(θ1,θ2,···,θn)T为其对应的可实现值.式(10)的初始条件为X(0)=x0,其中x0为确定性初始值.
根据概率守恒原理[20],记(X(t),Θ)的联合概率密度函数为pXΘ(x,θ,t),则其满足如下广义概率密度演化方程[21]
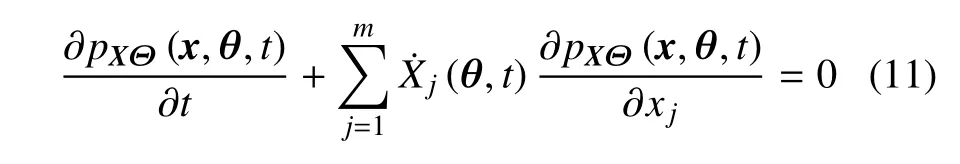
其初始条件为
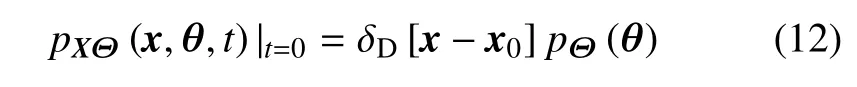
求解上述方程即可得X(t)的概率密度函数
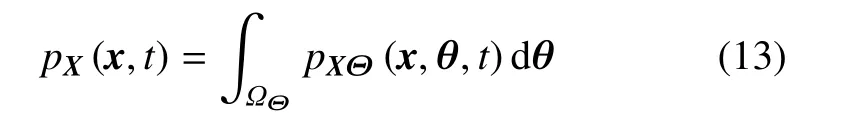
由此可见,若已知初始随机源概率信息(输入概率信息)pΘ(θ),即可通过求解式(11)、式(12)和式(13)获得输出概率信息pX(x,t).因此,上述3 个方程决定了从输入概率密度函数到输出概率密度函数的变换.从函数空间来看,即存在如下算子方程
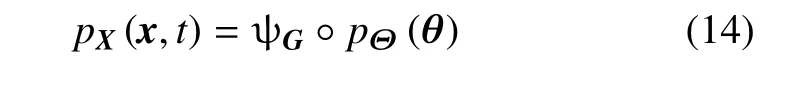
这里用下标G表示算子ψG由方程(10)所决定,而方程(10)是描述系统演化内在物理机制的方程.因此,从这一角度来看,概率密度演化理论[20-21]正是算子方程(14)的具体实现过程,而不确定性在系统中从输入概率信息到输出概率信息的传播,是由系统物理机制(通过确立传播算子)来决定的.从这一意义上说,ψG可称为不确定性传播算子.
事实上,式(9)和式(14)中的算子ψg和ψG,正是Frobenius-Perron 算子[21-22].值得注意的是,上述算子是线性算子,仅依赖于物理方程(例如以上的g(·)和G(·)),而与输入概率信息(例如以上pΘ(θ))的形式是无关的.换言之,物理系统本身不因随机源概率信息的变化而变化.这一随机系统客观不变性原理,正是上述不确定性传播算子具有不变性的内在原因[23].
2 基于Fr´echet 导数的整体灵敏度
2.1 基于Fr´echet 导数的整体灵敏度指标定义
基于上述泛函空间理解,Chen 等[16]提出了基于Fr´echet 导数的整体灵敏度指标.为清晰起见,下面以随机系统(10)与相应的不确定性传播算子方程(14)为基础简要阐述其基本思想.
考虑如下问题:若输入概率密度函数发生了变化,例如从pΘ(θ)变为˜pΘ(θ),则系统响应(输出)的概率密度函数也将相应地发生改变,且由算子方程(14)可知

为方便起见,记输入概率密度函数的变化为δpΘ=(θ)−pΘ(θ),输出概率密度函数的变化为δpX=(x,t)−pX(x,t).由式(15)两端分别减去式(14)可得由此可见,若输入概率信息具有变化,则输出概率信息的变化亦由不确定性传播之线性算子所决定.

事实上,上述概率信息“变化”的传播算子,就是不确定性传播算子的Fr´echet 导数,其严格的数学定义为[24]:
令V和W为Banach 空间,定义映射ψ:V→W.若存在一有界线性算子Fψ∈L(V,W),满足

则称Fψ为在u0∈U⊂V处的算子ψ 的Fr´echet 导数,记为Fψ=ψ′[u0].式中,∥·∥V和∥·∥W分别对应Banach空间V和W上的范数.
在本文中,Banach 空间V上的范数采用基于总变差距离的范数
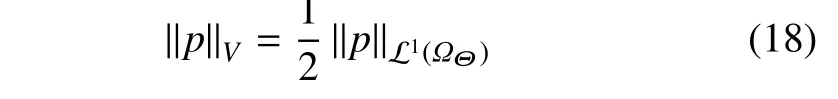
其中,L1(ΩΘ)为定义在ΩΘ上的ℓ1范数,即
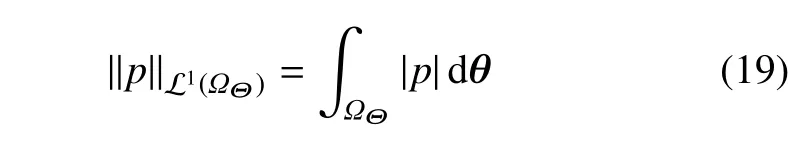
而空间W上的范数同样可定义为
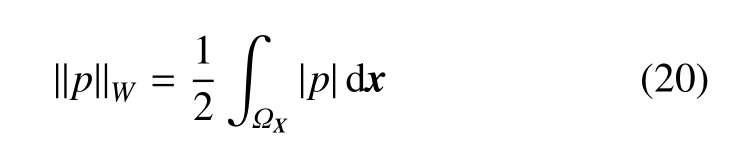
由于不确定性传播算子是线性算子,因此概率信息“变化”的传播算子就是不确定性传播算子本身.
在实际计算中,可以利用Fr´echet 导数与Gˆateaux导数的等价性.Gˆateaux 导数的定义为:令V和W为Banach 空间,定义映射ψ :V→W.若存在一有界线性算子Gψ∈L(V,W),满足

则称Gψ为在u0∈U⊂V处的算子ψ 的Gˆateaux 导数,记为Gψ=ψ′[u0].
显然,Fr´echet 导数即为Gˆateaux 导数.反之,若Gˆateaux 导数在点u0处连续或式(21)对h一致成立且∥h∥V=1,则点u0处的Gˆateaux 导数亦为Fr´echet导数[24].
无论是确定性系统还是随机系统,系统灵敏度的定义都可以阐述为[25]“系统灵敏度是输入量的扰动导致输出量的扰动这一效应的度量”.基于这一观点,在经典的确定性系统分析中往往采用函数的偏导数作为系统灵敏度的度量.显然,在随机系统中采用算子的Fr´echet 导数作为系统的灵敏度度量,乃是一种自然的推广.但是,以函数的偏导数作为确定性系统的灵敏度,仅能反映系统在给定输入值一点处的变化情况,因而是一种局部的度量;而对随机系统而言,Fr´echet 导数给出了在系统输入全部可能值(通过概率密度函数刻画)处的变化导致在系统输出全部可能值上的变化情况,因而其本质是一种整体灵敏度指标(global sensitivity index,GSI)[16].
基于Fr´echet 导数的整体灵敏度指标有4 个重要性质:
(1)无论物理系统本身是线性还是非线性的,因为Fr´echet 导数是线性算子,因此基于Fr´echet 导数的整体灵敏度指标与pΘ的具体形式是无关的(类似于线性函数x=kθ 中的局部灵敏度dx/dθ=k是与θ 取值无关的).这意味着,这一整体灵敏度指标不仅适用于输入概率密度信息具有小扰动的情况,也适用于输入概率密度信息具有大扰动、甚至若干输入变量从随机变量变为确定性变量的情况(例如概率密度函数坍塌为Dirac 函数).
(2)基于性质(1),若考虑输入概率模型具有某种程度的认知不确定性[1-2,17-18],例如,输入概率密度函数可能为,则这种认知不确定性传播的量化可以直接由该整体灵敏度指标给出,即Fψ◦(.
(3)对于随机动力系统,系统响应是时变的,因此基于Fr´echet 导数的整体灵敏度指标为一时变量.在此情况下,可根据问题的需要考虑系统响应的某代表性值,如系统响应时程的极大值,即Zext=max{X(t),t∈[0,T]},简记为Z.
(4)注意到Fr´echet 导数是线性有界算子,在式(17)、式(18)和式(20)定义下的范数为1(证明见第2.3 节).由于Fr´echet 导数就是不确定性传播算子本身,因此,不确定性传播算子的范数为1.这在本质上是概率守恒原理[20]在泛函空间观点下的数学表述之一.
2.2 整体灵敏度指标的参数化表达
在工程中,特别具有实际意义的是参数化表达的整体灵敏度指标.对绝大多数实际工程问题而言,系统输入参数Θ一般为连续型随机向量,记其概率密度函数为pΘ(θ;ζ),其中ζ=(ζ1,ζ2,···,ζs)T为其对应的分布参数向量.此时,pΘ(θ;ζ)的变分为
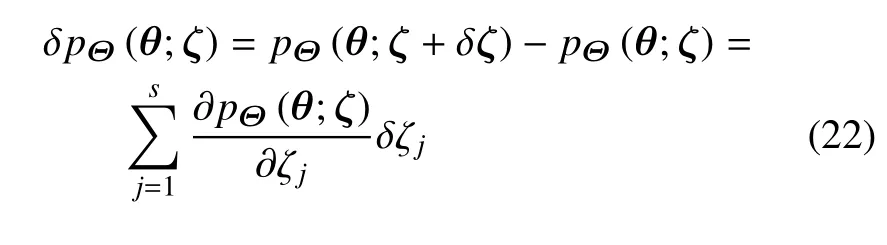
在文献[16]中,考虑各分布参数之间相互独立变化,即当仅考虑δζj≠0 而其他为0 时,给出了基于Fr´echet 导数的整体灵敏度指标的参数化表达

引入式(14),式(23)可以进一步改写为
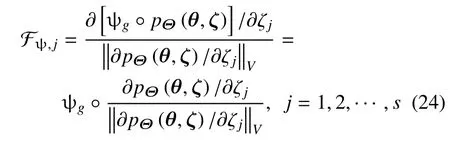
这表明基于Fr´echet 导数的整体灵敏度指标参数化表达是不确定性传播算子作用于单位化的输入函数变化上的结果.因此,上述整体灵敏度指标参数化表达的几何意义为单位化的输入函数变化作为抽象空间中的点(向量)经系统作用后的“方向”及“长度”变化.
更具体地,在实际工程问题中,有时通过随机变量Θ 的统计矩参数来近似构造其概率密度函数.例如,四阶矩正态变换方法假定随机变量Θ 可表达为标准正态随机变量U的多项式函数[26]

其中,参数a0,a1,a2和a3由Θ 的前四阶矩即其均值µΘ、标准差σΘ、偏度αΘ和峰度βΘ计算得到

由随机变量的函数变换法则[19-21],随机变量Θ的概率密度函数可表示为
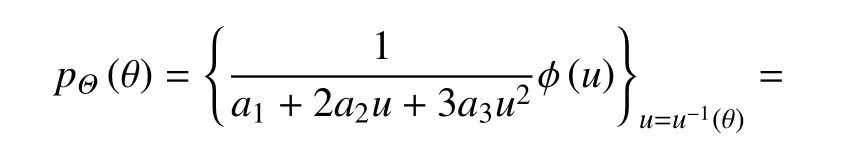
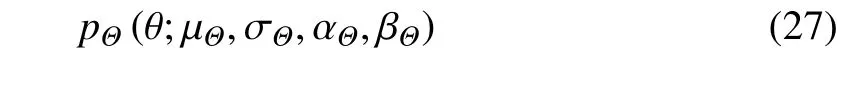
其中,ϕ(u)为标准正态分布的概率密度函数,反函数u=u−1(θ)的显式表达详见文献[27].
可见,此时Θ 的概率密度函数由其前四阶矩确定.不妨考虑随机向量Θ=(Θ1,Θ2,···,Θn)T相互独立,而对于非独立情况可通过Nataf 变换[28]、Copula函数[29]或随机函数模型[3]转换为独立情况.此时,该随机向量的概率密度函数可表示为
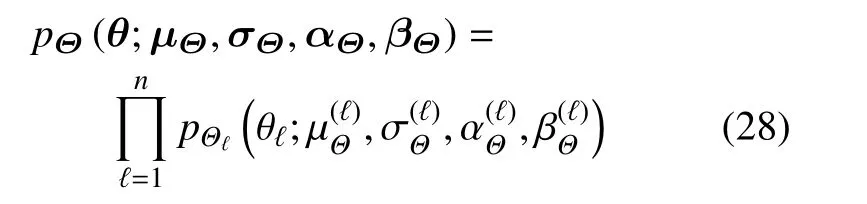
式中,pΘℓ为第ℓ 个随机变量Θℓ的概率密度函数,分别对应Θℓ的均值、标准差、偏度和峰度.由式(23)和式(28)可得随机系统(1)基于Fr´echet 导数的整体灵敏度指标为
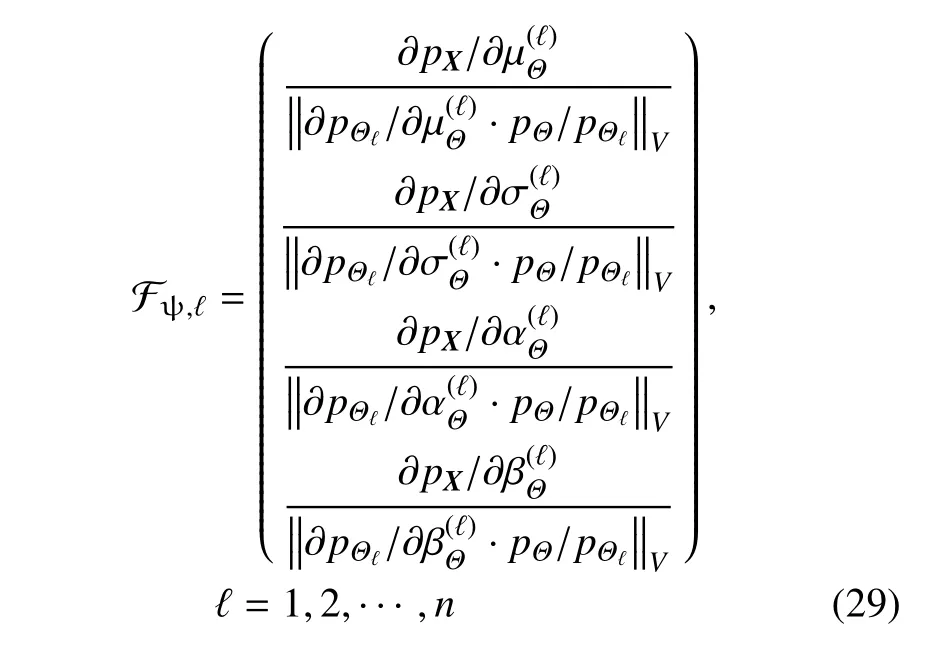
矩表达形式中前四阶矩的物理意义是十分明确的,其对应的全局灵敏度指标反映了各个输入变量的前四阶矩信息变化对输出概率密度函数的影响.
更一般地,若Θ的概率密度函数是已知的但是非参数化的,如pΘ(θ)是通过核密度估计[1]或概率密度演化理论[21]得到的数值解,则可通过ε-等效分布的方法将其参数化.为此,记随机变量Θ的概率密度函数为pΘ(θ).若Θ可以由有限个参数进行表达,则称(θ;ζ)为pΘ(θ)的ε-等效分布,满足
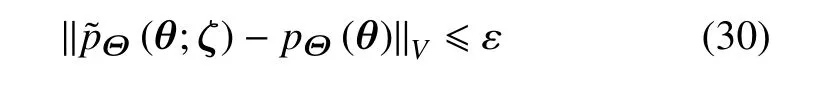
其中,ζ为有限维参数向量,可由优化算法[12]求解式(30)给出;ε 为给定的容许误差,如0.01.注意,这里(θ;ζ)可以是任意形式的.例如,有确定形式的概率密度函数[2-3]、由矩表达形式给出的概率密度函数[26-27]或由级数展开方法[30]计算得到的概率密度函数等.在上述基础上将pΘ(θ;ζ)替换为(θ;ζ),则随机系统(1)基于Fr´echet 导数的整体灵敏度指标的参数化表达可统一为式(23).
2.3 重要性测度
如式(23)所示的整体灵敏度指标描述了系统响应X的值域范围内每一点x处概率密度的灵敏度.进一步,对整体灵敏度指标取∥·∥W范数可得其重要性测度

现分别考察式(31)的几何意义和物理意义.
2.3.1 几何意义
考虑Fr´echet 导数的算子范数,其定义为[24]

式中各符号同式(17)中定义.任意取Θ的概率密度函数为p2和p1,令p=p2−p1,由均值定理有[24]
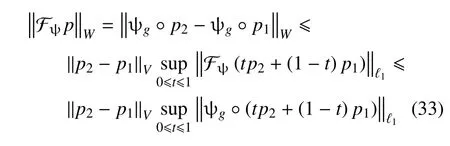
此处利用了不确定性传播算子是线性算子的性质.
注意tp2+(1 −t)p1为概率密度函数.因此,由概率相容性和不确定性传播算子方程(9)有
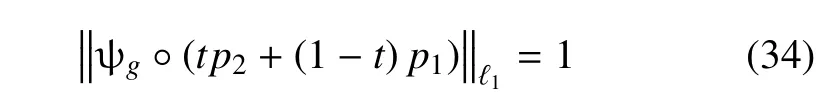

因此,重要性测度总是小于1.结合前述式(24)的几何意义表明,重要性测度的几何意义是单位化(即长度为1)的输入函数变化作为抽象空间中的点(向量)经系统作用后的长度,这一长度不可能超过1,且该长度越大,则其重要性越大.
2.3.2 物理意义

其中,ej为s维单位向量,且仅其第j位上元素为1而其它为0;dTV(p,q)为概率密度函数p和q的总变差距离(total variation distance),即[16]

类比于连续介质力学中的变形梯度并观察式(36)不难发现,由式(31)所定义的整体灵敏度对应的重要性测度反映了某种“体积变化率”(如图1 所示):当第j个分布参数ζj发生扰动,使得输入概率空间产生“体积变化”后,随机系统对应的输出概率空间亦相应地产生了“体积变化”,即.由式(36)定义可知,这两者的比值的物理意义便是由不确定性传播导致的“体积变化率”.需要注意的是,由式(36)定义的“体积变化率”恒为正值,因此可视其为“体积变化率”的绝对值或将其称为“幅值”.如此,由式(31)给出的整体灵敏度指标对应的重要性测度的物理意义是十分明确的.

图1 基于Fr´echet 导数的整体灵敏度指标对应的重要性测度的物理意义Fig.1 Physical meanings of the importance measure with respect to the Fr´echet derivative based GSI
2.4 方向灵敏度
另一方面,考虑如(23)所示的整体灵敏度指标在系统响应X值域范围内的方向灵敏度

式中,sgn(A)为符号函数:当A≥0 时取+1(代表“正”或“+”)、否则取−1(代表“负”或“−”).计算整体灵敏度指标在ΩX上的积分,易得

事实上,由式(31)可知
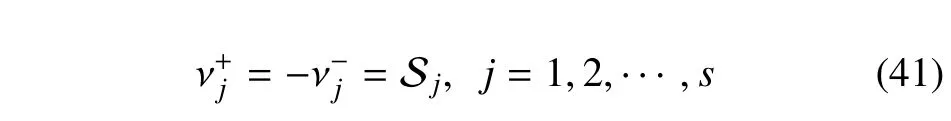

其中I{A}为示性函数,当A为真时取1,否则取0.
由式(38)所定义的方向灵敏度的意义在于,系统响应的值域ΩX可以通过式(42)划分为正、负两个子值域(可能是多连通域).具体而言:(1)输入分布参数的微小正增长,如∆ζj>0 将导致正值域内的概率密度函数增大、负值域内的概率密度函数减小;反之,输入分布函数的微小负增长将导致正值域内概率密度函数减小,而负值域内的概率密度函数增大.因此,与分别表示了由于参数变化导致的概率净减和概率净增值域;(2)若按式(38)定义可得有限个正、负值域,则正或负值域的不连续子值域个数(如图2)可反映物理系统的复杂程度.一般而言,系统非线性程度越复杂,其不交叉子值域个数越多.在第4 节将结合具体实例对其进行详细讨论.
2.5 与矩独立灵敏度指标的联系
考虑随机系统(1),基于矩独立的全局灵敏度指标定义为[10]

而此时pΘi与pΘ的总变差距离为
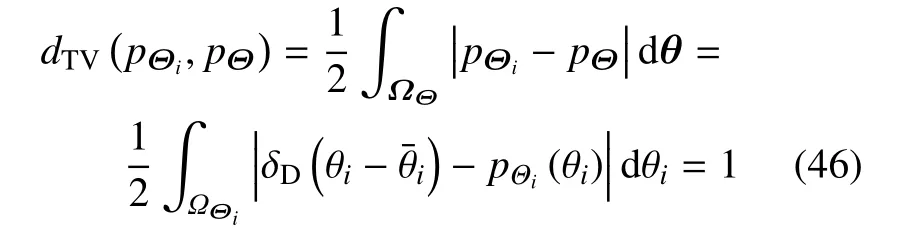
上式意味着当第i个随机变量Θi坍塌为确定性变量时,输入概率空间产生了单位体积的变化.此时,基于矩独立的全局灵敏度指标等价于
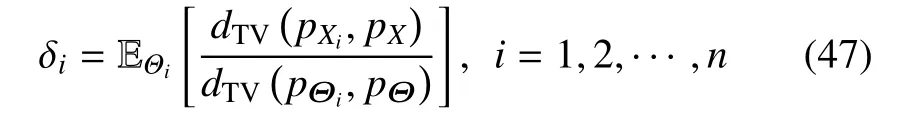
在第2.3 节中,式(36)解释了基于Fr´echet 导数的整体灵敏度指标的重要性测度的物理意义:它是随机系统在点pΘ处沿其分布参数ζj方向的(绝对)体积变化率.类比于此,式(47)可理解为第i个随机变量Θi沿其所有可实现值¯θi方向(绝对)体积变化的期望值.

在此理解的基础上,记第i个随机变量Θi向其均值µi坍塌前Θ的联合概率密度函数为pΘ(θ;µi,σi)、坍塌后为pΘi(θ;µi,0),则由均值定理有[24]
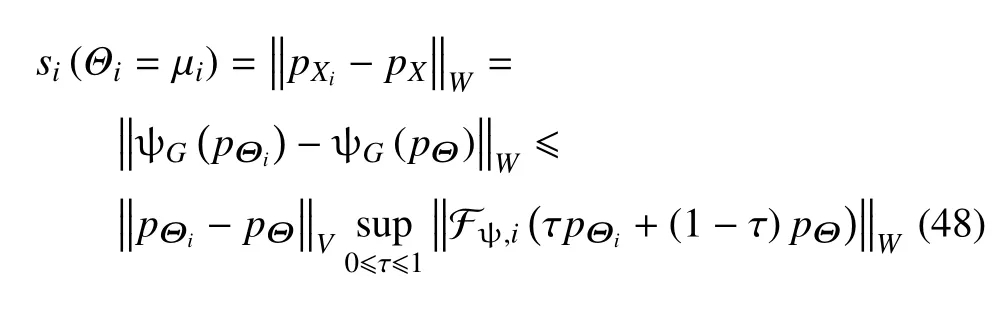
这里Fψ,i为基于Fr´echet 导数的整体灵敏度指标的参数化表达.注意到Fψ,i为一线性算子,式(48)可进一步写为
式中不等式右边两项分别对应点pΘi和pΘ处的关于标准差参数的重要性测度.在点pΘ处有

其中Si(σi)为由式(31)给出的第i个随机变量Θi关于其标准差参数σi基于Fr´echet 导数的整体灵敏度指标的重要性测度.
3 数值方法
基于Fr´echet 导数的整体灵敏度计算分为两部分:(1)系统响应的概率密度函数关于输入分布参数的导数;(2)输入概率密度函数关于分布参数的导数的范数.对于第(2)部分,由于˜pΘ(θ;ζ)是已知的,因此计算该范数项是容易的;而对于第(1)部分则可以通过中心差分法对其进行数值近似,即

对一些简单随机系统而言,可通过显式解析表达的Frobenius-Perron 算子[31]直接求解式(14),从而获得系统响应的概率密度函数.然而,对绝大多数实际工程问题而言,Frobenius-Perron 算子难以直接进行理论求解.因此,本文将基于概率密度演化理论(probability density evolution method,PDEM)[21]进行求解,从而获得pX(x),详见第3.1 节.
一般而言,对j=1,2,···,s分别进行概率密度演化分析即可获得基于Fr´echet 导数的整体灵敏度指标.这总计需要2Ns次确定性分析.具体而言,不妨考虑Θ为10 维独立的随机向量、且各随机变量均为两参数分布.一般取概率密度演化分析中的概率空间剖分数为500,则总共需要求解20000 次确定性物理系统!这毫无疑问地给实际工程问题分析带来了极大的挑战.最近,Chen 和Wan[17]从概率测度变换(change of probability measure,COM)的角度提出了降低确定性分析次数的方法,详见第3.2 节.
3.1 随机系统不确定性传播的概率密度演化理论
基于概率密度演化理论,对系统(10)的数值求解算法的基本步骤包括[21]:
(1)概率空间剖分与点集优选:记Θ的样本空间为ΩΘ,将其剖分为N个子域Ω1,Ω2,···,ΩN,并使其满足且对任意1≤p≠q≤N有Ωp∩Ωq=∅.对q=1,2,···,N,在每个子域中选取一个代表点,记为θq∈Ωq,并计算其对应的赋得概率.赋得概率定义为子域Ωq相对于全域ΩΘ的Voronoi体积,即
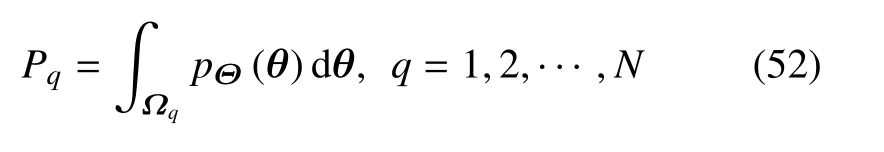
此步骤所涉及的点集优选策略及其点集误差分析可进一步见文献[32-33].
(2)对q=1,2,···,N,给定代表点θ=θq并求解系统(10)得到˙X(θq,t)=G(X(θq,t),θq,t).
(3)对q=1,2,···,N,求解半离散化的广义概率密度演化方程

需要说明的是,若考虑系统(10)的极值分布pZ(z),其中Z=max{X(t),t∈[0,T]}.此情况下,基于等价极值事件的基本思想、通过构造虚拟随机过程即可获得该极值分布pZ(z),详见文献[34].
3.2 随机系统不确定性传播的概率测度变换
3.3 基于Fre´chet 导数的整体灵敏度指标的概率密度演化概率测度变换算法
基于Fr´echet 导数的整体灵敏度指标的数值计算流程如下:

4 算例分析
4.1 算例一:正态随机变量的线性组合函数
考虑一随机系统

4.1.1 基于Fr´echet 导数的整体灵敏度指标
记相对于分布参数µ1,µ2和µ3的整体灵敏度指标分别为F (µ1),F (µ2)和F (µ3);相对于分布参数σ1、σ2和σ3的整体灵敏度指标分别为F (σ1),F (σ2)和F (σ3).本例中已知Θ1,Θ2和Θ3为正态随机变量,因此其ε-等效分布即为正态分布.基于Fr´echet 导数的整体灵敏度指标绘于图3 和图4 之中,对应的重要性测度如表1 所示,按其大小排序有:µ3>µ2=µ1以及σ3>σ2=σ1.从表中可见,所有的重要性测度均满足式(35),即其值不超过1.

图3 相对于均值参数的基于Fr´echet 导数的整体灵敏度指标(算例一)Fig.3 Fr´echet derivative based GSI in terms of the mean values(Example 1)

图4 相对于标准差参数的基于Fr´echet 导数的整体灵敏度指标(算例一)Fig.4 Fr´echet derivative based GSI in terms of the standard deviations(Example 1)
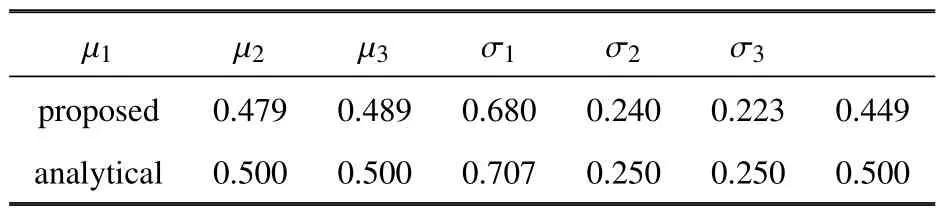
表1 基于Fr´echet 导数的整体灵敏度指标的重要性测度(算例一)Table 1 Importance measure of the Fr´echet derivative based GSI(Example 1)
在式(57)所示的随机系统中,各输入随机变量关于系统输出是线性且独立同分布的关系.因此,线性系数反映了各个输入随机变量与系统响应的物理关系.具体而言,分别就均值参数和标准差参数考察Θ1,Θ2和Θ3的重要性测度(表1)如下.

除了通过表1 计算所得的重要性测度外,直接观察图3 和图4 中整体灵敏度指标的峰值点亦能得到上述相关结论,即Θ1,Θ2和Θ3的重要性测度关于均值参数有比例关系、而关于标准差参数有比例关系1:1:2.
由式(38)所定义的方向灵敏度绘于图5 和图6 中.从图5 可见,F (µ1)与F (µ3)的方向是相同的、与F (µ2)的方向则是相反的.而在图6 中,F (σ1)、F (σ2)和F (σ3)的方向一致.主要原因如下:
(1)均值参数反映了随机变量的总体趋势.这意味着,若µ1或µ3有一个正增量∆µ,则在x<0 范围内的概率密度函数会相应地减小,而在x≥0 范围内的概率密度函数则会相应地增大,最终导致系统响应的概率密度函数整体向右移动;反之则反.这一结论,正是由物理方程(57)中Θ1,Θ2和Θ3前的符号“+”、“−”和“+”所决定的.
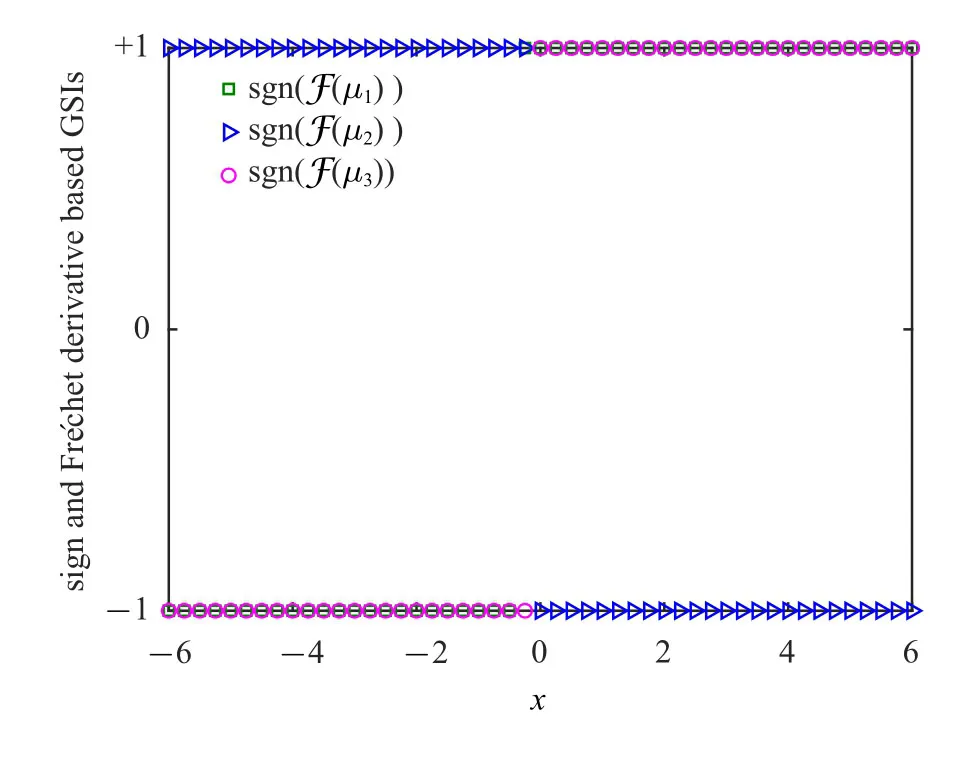
图5 相对于均值参数的基于Fr´echet 导数的整体灵敏度指标的方向灵敏度(算例一)Fig.5 Direction sensitivity of the Fr´echet derivative based GSI in terms of the mean values(Example 1)
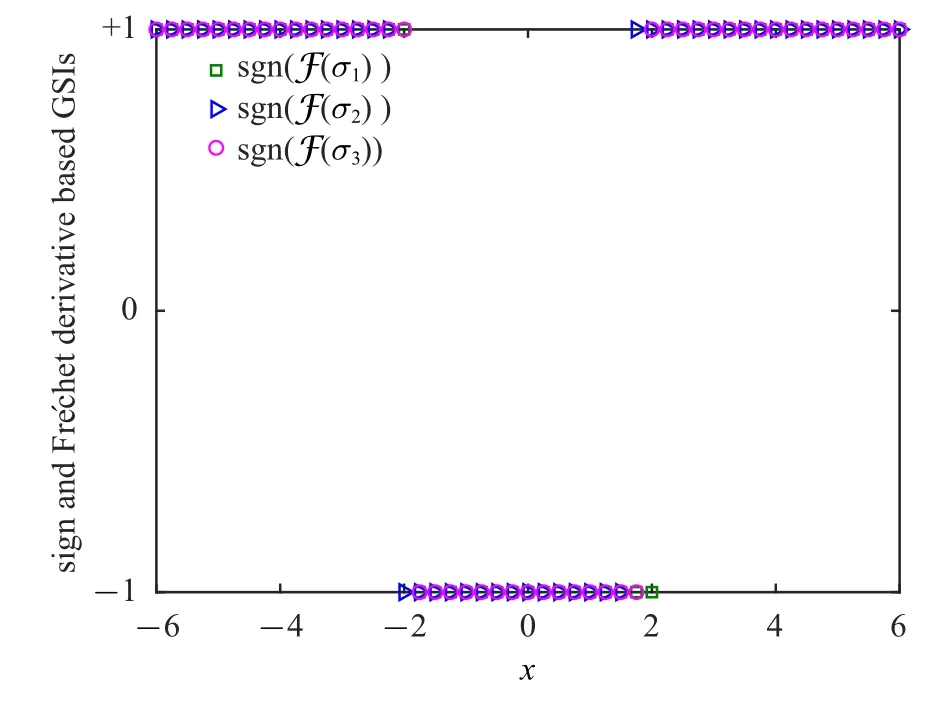
图6 相对于标准差参数的基于Fr´echet 导数的整体灵敏度指标的方向灵敏度(算例一)Fig.6 Direction sensitivity of the Fr´echet derivative based GSI in terms of the standard deviations(Example 1)
(2)对于标准差参数而言,由图6 可知,增大σ1,σ2或σ3均会使得x∈(−2,+2)范围内的概率密度函数相应地减小,而x∈(−∞,−2]∪[+2,+∞)范围内的概率密度函数会相应地增大,最终导致系统响应的概率密度函数变得更为扁平.换言之,本例中系统响应标准差将随着σ1,σ2或σ3的增大而增大.显然,由可知这一结论是正确的.
4.1.2 与矩独立灵敏度指标的关系
考虑随机系统(57)的矩独立灵敏度指标[10],对i=1,2,3,si(Θi=µi)分别为
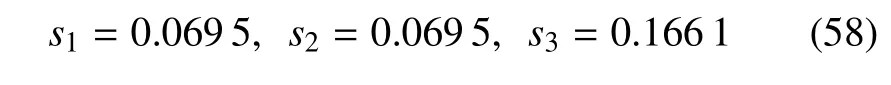
需注意的是,虽然本例中分布参数µ1和µ2的重要性测度相同,但它们的方向灵敏度是相反的.可见,单凭重要性测度提供的灵敏度信息是不够充分的,这侧面反映了基于Fr´echet 导数的整体灵敏度指标的优越性.
4.2 算例二:隧道锚杆支护系统
考虑一隧道锚杆支护系统[27,36],如图7 所示,假定系统是轴对称与各向同性的.在岩体压力Prock、喷浆混凝土衬砌承压力Pshot与锚杆承压力Pbolt的共同作用下,该支护系统的功能函数可表达为[36]
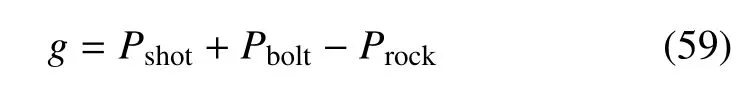

图7 隧道锚杆支护系统Fig.7 Rock bolting system of the tunnel
式中,岩体压力Prock可隐式表达为[36]
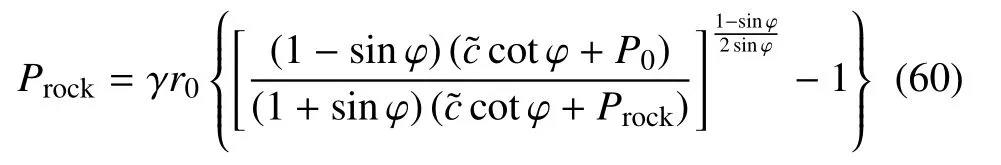
其中P0为地应力,为修正后岩体有效黏聚力,有
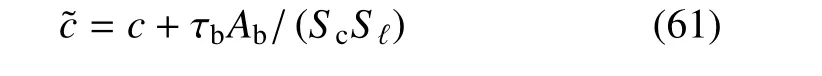
喷浆混凝土衬砌承压力Pshot为径向变形的函数
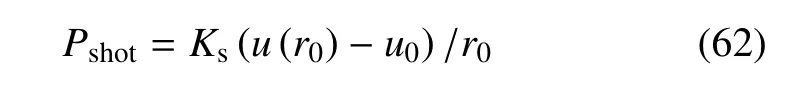
其中,Ks为支护刚度模量(考虑d≪r0)
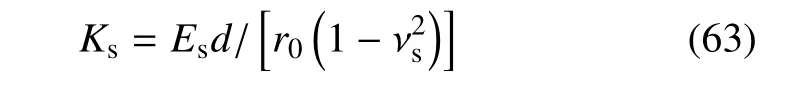
式(62)中u(·)为径向变形场,它是离隧道中心距离r的反比例函数,即
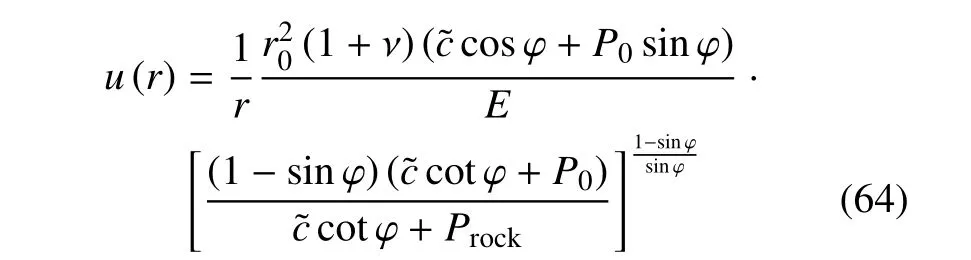
锚杆承压力Pbolt按下式计算
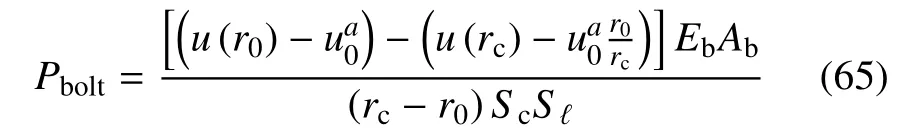
式(59)∼式(65)中各确定性模型参数取值及其物理意义详见表2.
此外,考虑式(59)∼式(65)中的地应力P0(MPa)由四阶矩正态变换方法进行表征[27],其前四阶矩分别为µP0=9.975,σP0=2.300,αP0=−0.249 1和 βP0=2.874 8;岩体弹性模量E(GPa)服从对数正态分布,其均值为µE=4.370,标准差为σE=0.524 4;初始径向位移u0(cm)服从对数正态分布,其均值为µu0=3.200,标准差为σu0=0.400.通常,对数正态分布的概率密度函数为

表2 隧道锚杆支护系统确定性参数(算例二)Table 2 Deterministic parameters in the rock bolting system of the tunnel(Example 2)[36]
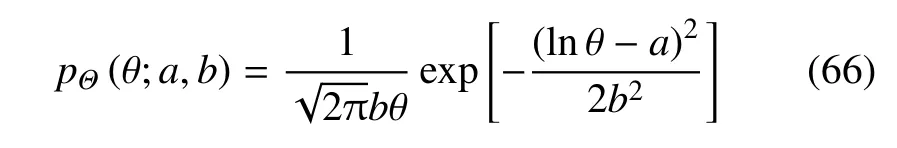
因此,实际分析中对数正态分布函数的参数a和b按下式进行换算[18]
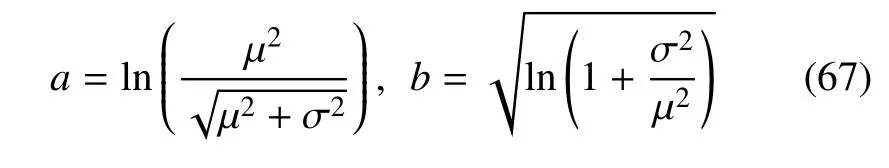
其中µ为均值、σ 为标准差.记E的分布参数为aE和bE,u0的分布参数为au0和bu0,由式(67)计算得到.本例灵敏度分析结果绘于图8 和图9 之中.
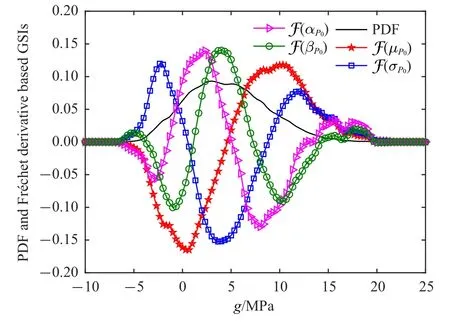
图8 相对于参数P0前四阶矩的基于Fr´echet 导数的整体灵敏度指标(算例二)Fig.8 Fr´echet derivative based GSI in terms of the first fourth-moments of the parameter P0(Example 2)

图9 相对于参数E 和u0的分布参数a 和b 的基于Fr´echet导数的整体灵敏度指标(算例二)Fig.9 Fr´echet derivative based GSI in terms of the distribution parameters a and b of the parameters E and u0(Example 2)
本例中的8 个分布参数的重要性测度排序为
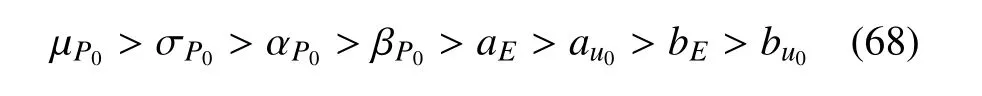
对应的重要性测度分别为0.910 5,0.793 8,0.713 6,0.635 3,0.275 9,0.161 1,0.122 5 和0.086 2,且均满足不超过1 的性质.可见,地压力P0对功能函数的影响是最大的,次之为岩体弹性模量E和初始径向位移u0.另一方面,从图8 和图9 可以进一步观察到:
(1)相较于低阶矩而言,高阶矩参数对响应概率密度函数的影响更为复杂,即其方向灵敏度有更多的不相交正值域或负值域.
(2)若仅考虑均值分布参数,可以看到参数P0将使得g的概率密度函数向正向移动,而参数E则使g的概率密度函数向负向移动.这一点可以在锚杆承压力计算式(65)与径向变形场式(64)中得以理解:当P0增大或E减小时,径向变形增大,从而使得锚杆承压力Pbolt增大,最终导致g增大,因而其概率密度函数向正向移动.
4.3 算例三:大坝下稳态受限渗流模型
考虑一个大坝下稳态受限渗流分析模型[14,37],如图10 所示.在分析中,假定渗流是各向同性和均匀的、且渗流仅发生在AB段和CD段.记粉质碎石层的透水率为Tg,x(x方向)和Tg,y(y方向);粉质砂土层的透水率为Ts,x(x方向)和Ts,y(y方向).记AB段的水头差为hW=hD+20,则AB段到CD段的渗流控制方程为[14]

图10 大坝下稳态受限渗流模型的原理图[14]Fig.10 Schematic representation of the steady-state confined seepage below the dam [14]

本文用有限元法(共计3413 个节点,1628 个单元)求解式(69)所示控制方程[14]得到分析区域的水头差分布函数hW(x,y),最后计算渗流量q
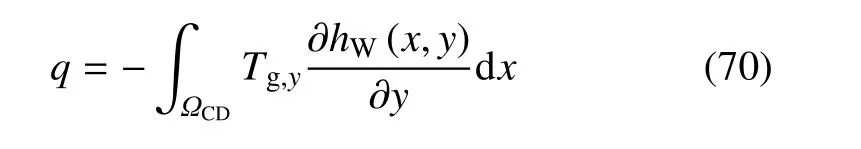
其中q的单位为L/(h·m).式(69)各参数取值列于表3 中,其中U(7,10)为区间[7,10]上均匀分布,LN(µ,σ)为均值为µ、标准差为σ 的对数正态分布.

式中B(ah,bh)=Γ(ah)Γ(bh)/Γ(ah+bh),Γ(·)为Gamma 函数.

表3 大坝下稳态受限渗流模型参数(算例三)Table 3 Parameters in the dam model of the steady-state confined seepage(Example 3)[37]
灵敏度分析结果绘于图11 与图12 中.由表4 可知,按参数a进行重要性测度排序有
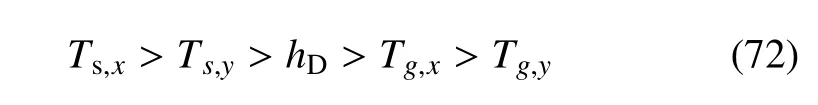
而按参数b进行重要性测度排序有

这意味着:(1)粉质砂土层透水率是非常重要的参数、而粉质碎石层透水率则是相对而言重要性较低;(2)除在hD中二者接近外,参数a相较于参数b更为重要.但同样所有变量的重要性测度也均不超过1.

图11 相对于参数a 的基于Fr´echet 导数的整体灵敏度指标(算例三)Fig.11 Fr´echet derivative based GSI in terms of the parameter a(Example 3)
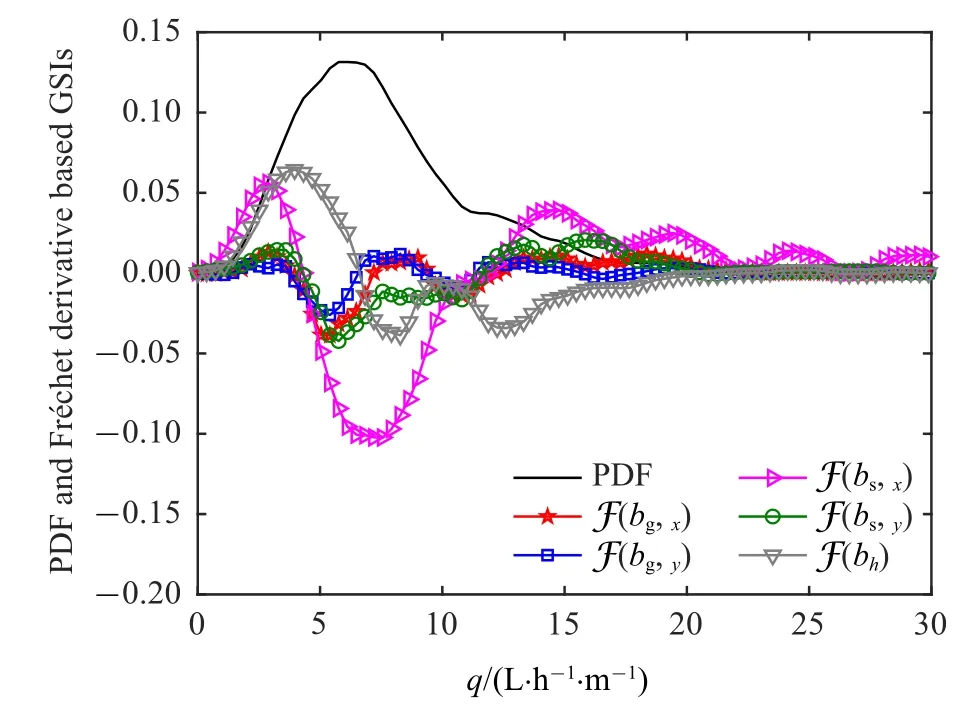
图12 相对于参数b 的基于Fr´echet 导数的整体灵敏度指标(算例三)Fig.12 Fr´echet derivative based GSI in terms of the parameter b(Example 3)

表4 基于Fr´echet 导数的整体灵敏度指标的重要性测度(算例三)Table 4 Importance measure of the Fr´echet derivative based GSI(Example 3)
4.4 算例四:钢筋混凝土平面框架结构
考虑一榀钢筋混凝土平面框架结构,见图13.结构底层柱截面为600 mm×800 mm、二层柱截面为500 mm×700 mm,其他层柱截面为500 mm×600 mm;中跨梁截面统一设计为300 mm×450 mm、边跨梁截面均采用300 mm×600 mm.截面配筋信息详见文献[17].采用OpenSEES 软件对其进行有限元建模,具体而言:(1)单元类型设置为纤维梁单元;(2)采用与混凝土结构设计规范[38]对应的混凝土单轴损伤本构模型(“ConcreteD”命令)模拟混凝土材料的应力−应变关系;(3)考虑各向同性强化的Giuffe-Menegotto-Pinto模型[17]模拟钢筋材料的应力−应变关系(“Steel02”命令).
分析中,考虑第1 层,第2 层,第3 ∼6 层及第7 ∼10 层的混凝土材料的抗压强度fc1,fc2,fc3和fc4为独立同分布的随机变量,其概率信息详见表5.注意到混凝土弹性模量Ec(104MPa)与其抗压强度fc(MPa)是相关的.本例中,采用混凝土结构设计规范中建议的经验关系[38],即
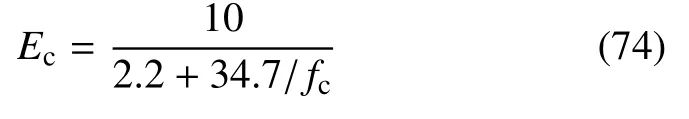

图13 钢筋混凝土平面框架结构[17]Fig.13 Reinforced concrete frame structure[17]
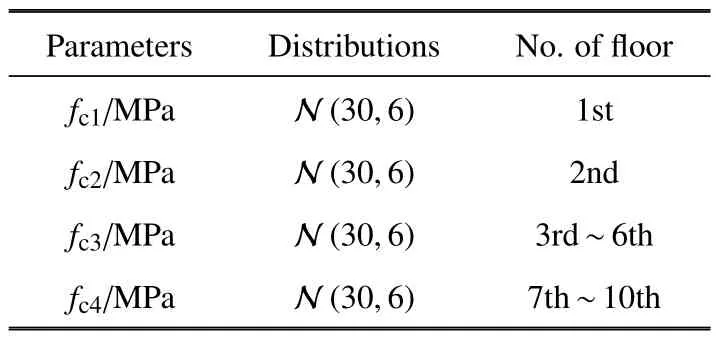
表5 混凝土抗压强度参数(算例四)Table 5 Parameters in the reinforced concrete frame structure(Example 4)
考察该结构在南北向El Centro 地震波作用下的随机动力响应,地震动幅值调整为中震作用下对应的0.2 g.记感兴趣量为顶层位移响应dtop(t)的极值,即其中为∞范数.
表中,N(µ,σ)代表正态分布,µ 为均值,σ 为标准差,并对i=1,2,3,4,记fci的均值参数为µi,标准差参数为σi.
本例分析结果如图14 和图15 所示,所得整体灵敏度指标的重要性测度列于表6 之中.同样,计算所得的各重要性测度均不超过1.可见,与fc2和fc3相比,fc1和fc4对顶层位移响应极值的影响更大,且尤以fc4影响最大.有意思的是,对底层位移做灵敏度分析,即取dext=∥dbottom(t)∥∞,此时相对于均值与标准差参数的重要性测度如表7 所示.此时,底层位移响应极值几乎完全由fc1所影响.表8 给出了在0.1g峰值加速度下底层位移与顶层位移的重要性测度(此时结构响应基本处于线性状态).值得注意的是,此时除fc1外,fc3和fc4均对底层位移响应极值的重要性测度亦有不可忽略的影响.
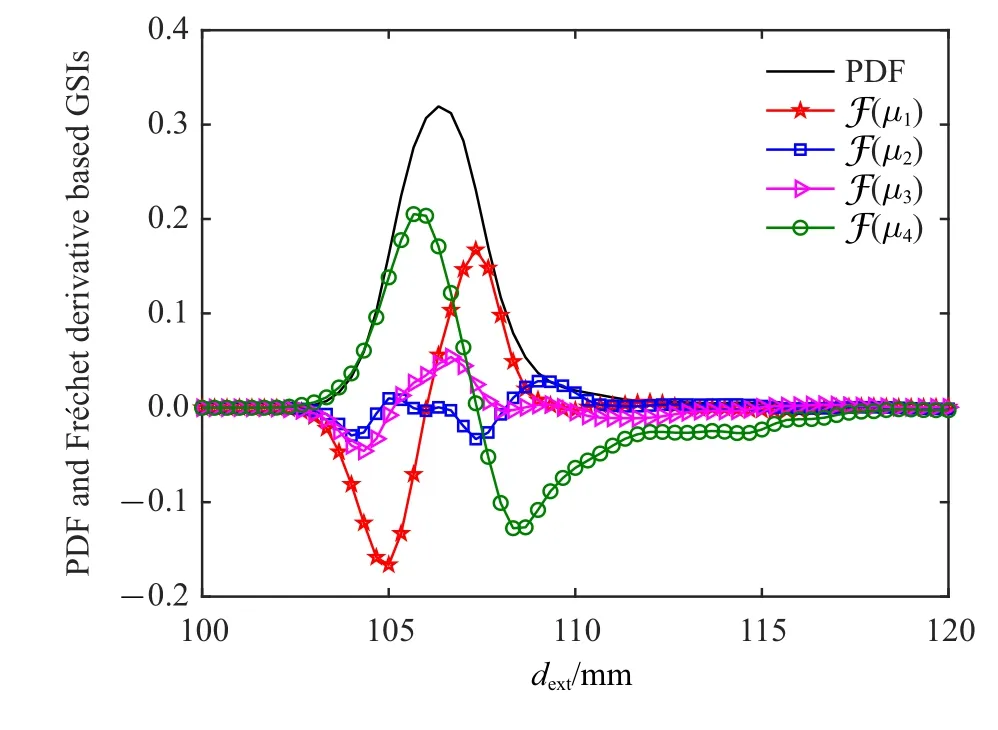
图14 相对于均值的基于Fr´echet 导数的整体灵敏度指标(算例四)Fig.14 Fr´echet derivative based GSI in terms of the mean value(Example 4)
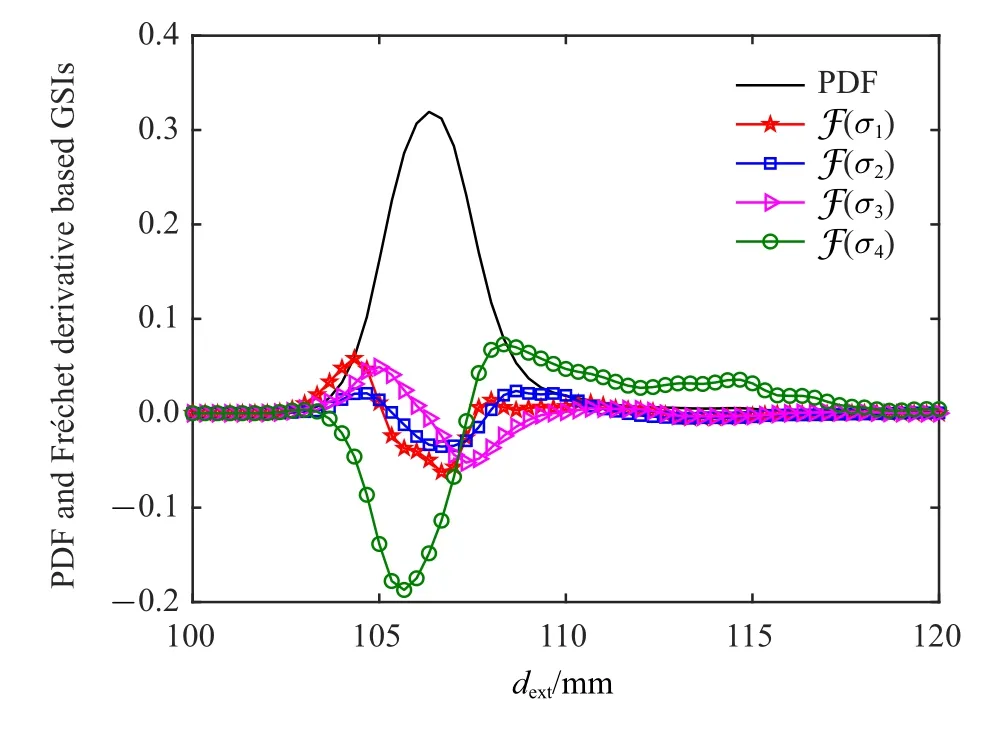
图15 相对于标准差的基于Fr´echet 导数的整体灵敏度指标(算例四)Fig.15 Fr´echet derivative based GSI in terms of the standard deviation(Example 4)

表6 基于Fr´echet 导数的整体灵敏度指标的重要性测度(算例四/顶部位移/0.2g)Table 6 Importance measure of the Fr´echet derivative based GSI(Example 4/top displacement/0.2g)
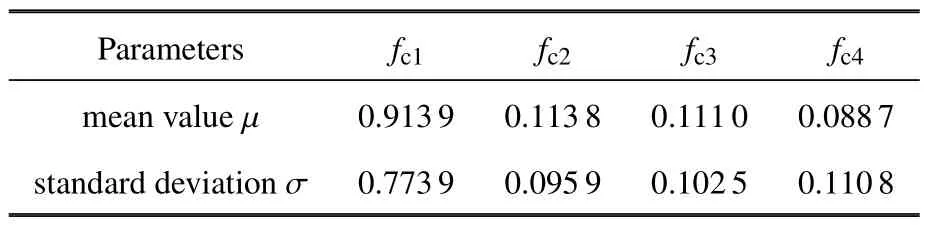
表7 基于Fr´echet 导数的整体灵敏度指标的重要性测度(算例四/底部位移/0.2g)Table 7 Importance measure of the Fr´echet derivative based GSI(Example 4/bottom displacement/0.2g)

表8 基于Fr´echet 导数的整体灵敏度指标的重要性测度(算例四/0.1g)Table 8 Importance measure of the Fr´echet derivative based GSI(Example 4/0.1g)
从定性上看,这可能是由于结构在中震作用下进入了一定程度的非线性[11],且非线性主要表现在混凝土材料中,如图16 所示.这也再次表明随机系统的整体灵敏度与物理系统的复杂程度密切相关,且在非线性与随机性耦合情况下,灵敏度指标排序可能出现与线性情况下不同的结果.
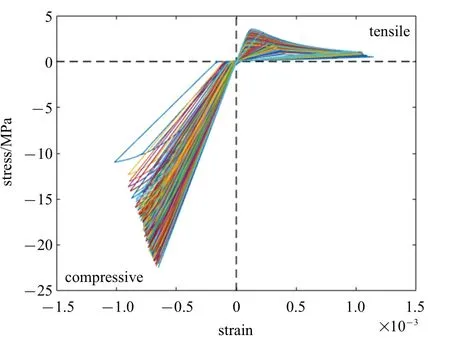
图16 某底层柱混凝土材料的应力−应变曲线(算例四)Fig.16 Stress-strain curves of concrete materials of one bottom column(Example 4)
5 结论
基于随机系统中不确定性传播的泛函观点及其泛函表达,引入了基于Fr´echet 导数的整体灵敏度指标.进一步,通过定义ε-等效分布,讨论了该整体灵敏度的参数化表达形式,定义了其对应的重要性测度与方向灵敏度,并论述了其物理意义.结合概率密度演化理论(PDEM)和概率测度变换(COM),具体给出了该整体灵敏度对应的数值计算方法.通过4 个算例对该整体灵敏度的工程实用性进行了分析与论证.本文主要结论如下:
(1)与传统整体灵敏度不同的是,本文所提整体灵敏度可看作是灵敏度分析从确定性系统到随机性系统的一个自然延拓,因而更具有物理指导意义.
(2)特别地,本文所提整体灵敏度不仅能反映系统响应空间中任一点处的灵敏度,亦能通过其重要性测度给出宏观的重要性排序、或通过其方向灵敏度标定特定的设计区域.而且,通过理论证明重要性测度不超过1.因此,该整体灵敏度所包含的不确定性量化信息十分丰富.
(3)概率密度演化理论与概率测度变换具有良好的计算精度与分析效率,可用于解决实际工程的灵敏度分析问题.
此外,如何根据实测数据进行灵敏度分析、如何确保高维概率空间下PDEM-COM 方法的计算精度、以及如何考虑非精确概率模型下的灵敏度分析等一系列问题,还有待进一步深入研究.

