基于DEM-FEM 耦合方法的海上风机结构冰激振动分析1)

杨冬宝 高俊松 刘建平 宋 础 季顺迎,2)

∗(大连理工大学工业装备结构分析国家重点实验室，辽宁大连 116023)

†(中国三峡新能源(集团)股份有限公司，北京 100053)

∗∗(上海勘测设计研究院有限公司，上海 200434)

引言

海上风能是最具有发展前景的可再生资源之一.我国漫长的海岸线和丰富的海风资源，为发展海上风电提供了有力的条件.虽然我国海上风电发展起步晚，但是自2018 年以来，我国海上风电新增装机量已经超过英国和德国，成为全球最大的海上风电发展市场.

传统的海上风机设计主要考虑空气动力、水利环境和抗震设计等外界因素[1-2]，但是对于我国渤海及黄海北部寒区海域的风机设计，海冰也是无法忽略的重要因素之一.虽然在一些寒区风机抗冰设计中已经采用极端静冰载荷校核风机结构抗冰性能，但是大量现场观测和理论研究表明，由海冰引起的冰激振动对海洋结构和设备的危害远远超过极端静载荷下结构整体安全问题[3].此外，现场测量和模型实验表明直立或锥体基础的海洋平台结构都会发生强烈的冰激振动，相比于锥体结构的随机振动，直立结构的稳态振动对于结构的危害更为严重[4-5].

海上风机结构主要分为适用于浅水海域的基础固定式风机和适用于较深海域的浮式风机[6].在各种风机结构中，单桩式风机是目前国内外应用最为广泛、研究最为集中的风机结构.对于风机与海冰的相互作用，其研究工作最早开始于20 世纪80年代丹麦、芬兰和挪威等北欧国家[7].通过一系列单桩风机基础与海冰相互作用的模型试验探讨了不同风机基础结构模型的动力学特性和冰载荷特点[8-9].近些年来，随着数值模拟技术的快速发展，Wang[10]采用Karna 冰力谱模型分析了冰载荷与风载荷对于风机疲劳的影响，得到冰载荷对于风机结构的振动响应和疲劳损伤的影响大于风载荷所造成的影响的结论；Shi 等[11]将半经验海冰--结构作用模型与HAWC2 程序相耦合研究了具有抗冰锥的单桩式风机在不同冰速、冰厚工况下风机结构的动力响应.此外，美国能源部国家可再生能源实验室(NREL)的FAST 风机软件也引入了基于Määttänen-Blenkar 海冰模型IceDyn 模块计算风机的冰载荷[12].相比于国外，国内对于风机研究主要通过数值模拟和室内模型试验进行研究[13].天津大学在低温冰水池对于不同直径单桩风机基础开展模型试验，重点验证各种冰载荷规范对于单桩风机适用性[7].一些国内学者基于风力谱和冰力函数也对各种固定式风机进行振动时域响应分析[14-16].

基于经典的海冰力学模型或冰力函数研究海冰与风机结构的相互作用更多侧重于结构的响应，而对海冰破坏方式给予了大量的假设.近年来，基于非连续力学的离散元方法被广泛地应用于海冰数值模拟中来有效模拟海冰破碎现象[17-18]，其中采用粘结--破碎特性的球体离散单元可以合理准确地模拟海冰与复杂海洋平台结构、船体结构等相互作用过程[19-20].风机结构在海冰激励下复杂的动力学响应计算可以采用有限元方法计算，因此基于计算参数传递的DEM-FEM 界面耦合模型[21]可计算单桩式风机结构的冰激振动.

为此，本文采用DEM-FEM 耦合方法建立海冰与单桩式风机的耦合模型，探讨不同冰速、冰厚下单桩式风机的冰载荷及风机轮毂和下部桩基的冰激振动响应特征.

1 单桩式风机冰激振动的数值方法

在对风机整体结构的冰激振动特性模拟中，风机采用有限元方法进行动力学分析，海冰采用离散元方法模拟，两者通过计算参数传递实现耦合分析.

1.1 海冰离散元方法

本文主要研究平整冰与风机相互作用过程，其中将平整冰模型离散为具有粘结--破碎特性的等直径球体单元.为合理地模拟实际海域内海冰的边界条件，对DEM 海冰模型的两侧边界的球形单元给予y和z方向上固定的位移约束，后侧给予恒定的流速，如图1(a)所示.颗粒之间采用平行粘结模型[22]传递单元间的作用力，如图1(b)所示.平行粘结模型之间的最大拉应力和最大剪应力可以通过经典梁的拉伸、扭转和弯曲理论计算，即

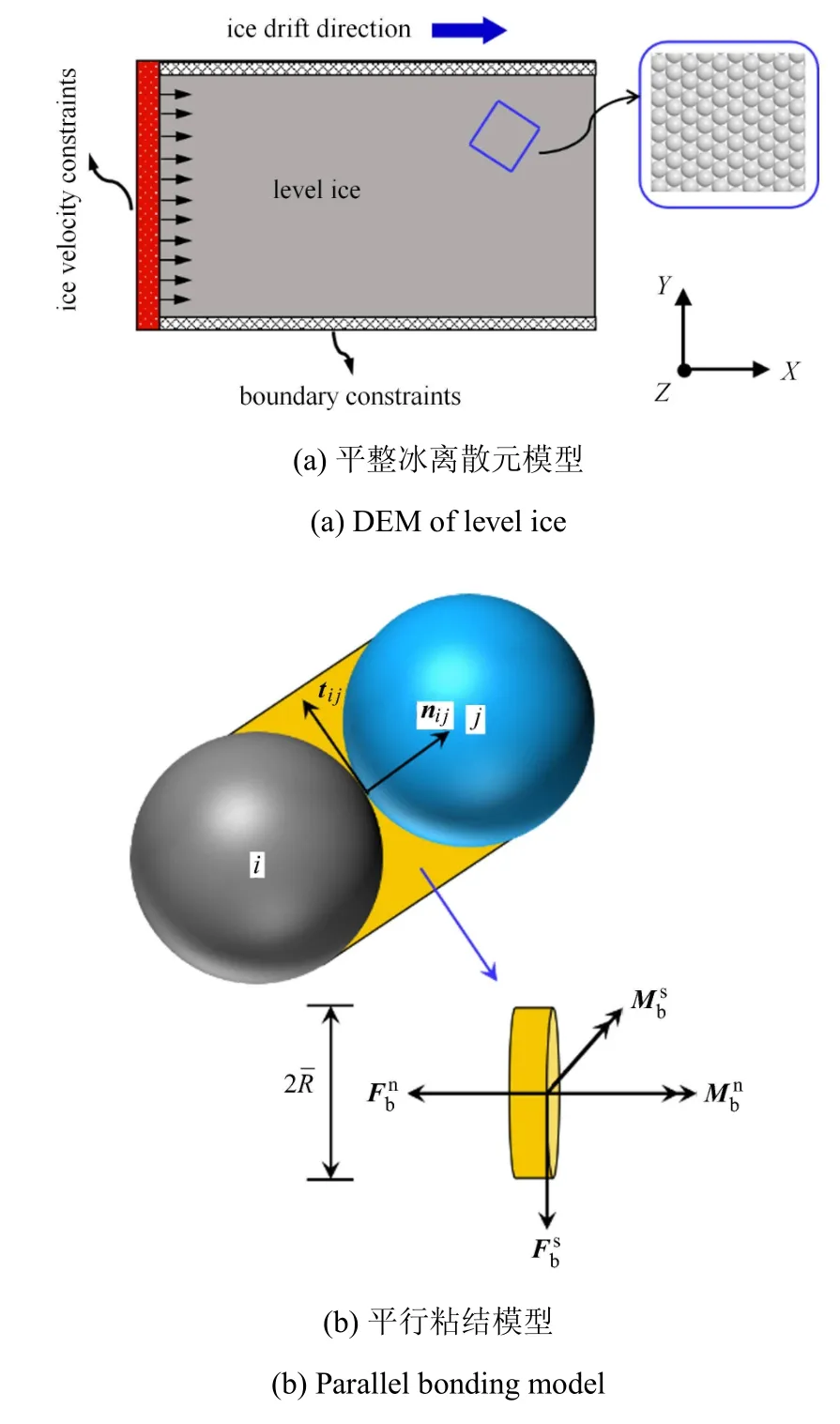
图1 海冰离散元方法Fig.1 DEM of sea ice

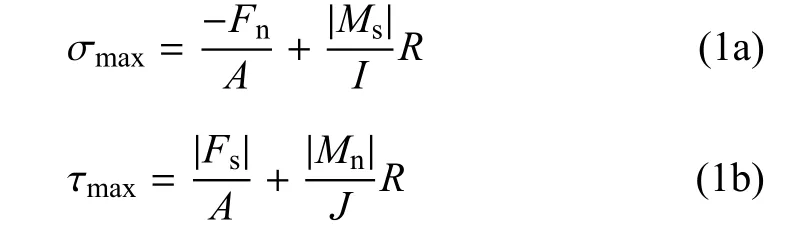
式中，Fn和Fs为粘结颗粒之间的法向和切向力；Mn和Ms为粘结颗粒的法向和切向力矩；A，R，J和I分别为粘结颗粒之间的粘结面积、等效粘结半径、极惯性矩和惯性矩.

海冰离散元方法通过单元间的粘结失效模拟海冰内部裂纹的生成和扩展，其中采用拉剪分区断裂准则对颗粒粘结失效进行判断[23]，如图2 所示.当两个粘结颗粒之间的最大拉应力σmax或剪切应力τmax达到材料拉伸破坏强度σt或剪切破坏强度τt时，颗粒间的粘结失效海冰发生破坏.这里，粘结颗粒间的拉伸破坏强度σt和剪切破坏强度τt表示为

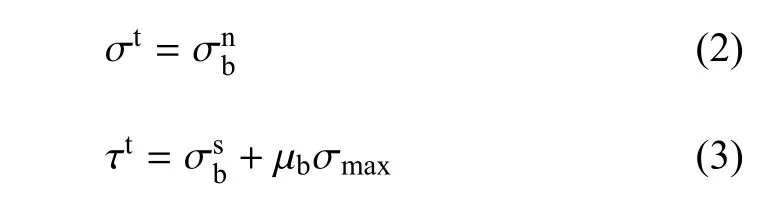
图2 拉剪分区断裂准则Fig.2 Fracture criterion with tensile and shear partition

海冰离散元参数σb和µb的选取直接影响海冰宏观物理力学性质.通过DEM 模拟海冰的单轴压缩试验和三点弯曲试验，可以得到海冰宏观强度与颗粒直径D、粘结强度σb、颗粒间摩擦系数µb等离散元微观参数的关系，其可写作[24-25]

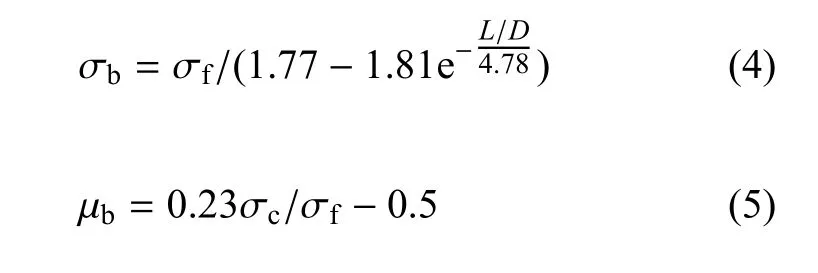
式中，σf和σc为海冰的弯曲强度和压缩强度；尺寸L可视为海冰的厚度，则L/D为平整冰中单元层数.

1.2 单桩式风机结构的有限元模型

建立带有抗冰锥体的单桩式风机的有限元模型，该模型主要由桩基、抗冰锥、塔筒和轮毂叶片4 部分组成，如图3(a)所示.为保证单桩式风机结构几何形状和整体结构振动响应的真实性，对风机的桩基和上部轮毂叶片作了适当的简化.风机桩基和塔筒等主体部分由梁单元构造；叶片由三角形单元构造，叶片单元仅为保证结构模型几何完整性不做动力学计算.风机抗冰锥体采用三角形平板壳单元进行有限元分析计算，其结构模型如图3(b)所示.综上所述，本文采用的单桩式风机模型主要由梁--壳组合单元构造，共有1229 个单元节点和1933个单元，风机各部分详细信息列于表1 中.

图3 单桩式风机有限元模型Fig.3 FEM of monopile-type wind turbine

表1 风机结构有限元模型的主要参数Table 1 Main parameters of finit element model Information of OWTs

为重点考虑风机在海冰作用下的振动特性，忽略空气动力载荷和水动力载荷，并且采用6 倍桩径法建立风机桩--土系统约束.此外风机上部的轮毂叶片的原型质量为213.7 t，简化为一个集中质量单元.表2 列出简化后模型的前5 阶自振频率.

表2 单桩式风机振动模态Table 2 Vibration mode of monopile-type wind turbine

采用Newmark 隐式积分求解算法对于风机动力学方程求解，结构的动力学方程为

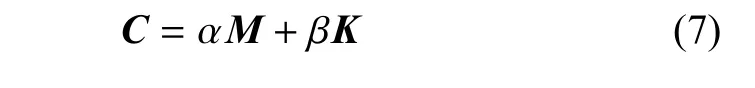
式中，参数α 和β 通过结构的模态阻尼比和固有频率计算得到，即α=0.171，β=0.014 6.

1.3 DEM-FEM 耦合模型

本文所采用的DEM-FEM 耦合算法是基于原耦合异步方法的基础上[21].通过CUDA C++语言建立CPU-GPU 协同处理并行计算架构的DEM-FEM界面耦合模型.基于界面参数传递的DEM-FEM 耦合算法在有限元和离散元计算中需要二者进行参数信息传递达到强耦合的效果.在有限元计算中，需要实时获得离散单元与结构之间的接触力、接触单元编号和局部接触点等信息；同时在离散元计算中，又需要更新结构的坐标和单元速度信息，如图4 所示.但是，GPU 设备端的DEM 并行计算所得到载荷信息结果是随机分配在各个线程中，使得界面之间参数传递效率低下.本文采用CUDA 的Thrust 函数中inclusive scan 和sortbykey 函数对界面之间的参数进行高效的基数排序[21]，实现离散元与有限元之间高效的参数传递.

图4 基于GPU 并行的DEM-FEM 耦合算法框架Fig.4 Schematic of a GPU-based parallel algorithm of coupled DEM-FEM

2 单桩式风机冰载荷分析及验证

2.1 风机冰载荷分析

海洋风机的冰载荷和冰激振动与海冰的厚度和速度有着密切关系[12].针对50 年一遇海冰厚度为0.374 m，平均冰速为0.3 m/s[15,26]，本文依照冰速和冰厚两个变量划分20 种工况，具体参数列于表3.此外，在流体动力学方面，考虑水对海冰的拖曳力Fd和浮力Fb，表示为

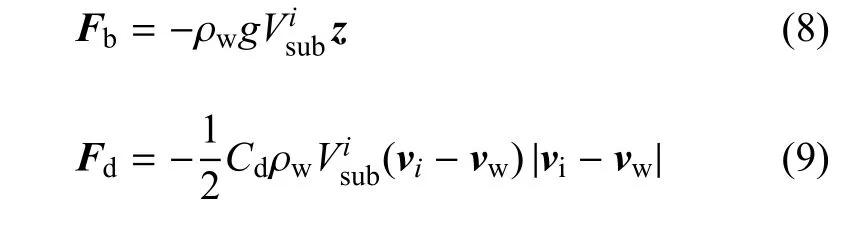
式中，ρw为海水密度；为单元i浸入水体积；Cd为流对冰的拖曳系数；和vw为海冰和水的速度；z为向上单位矢量.

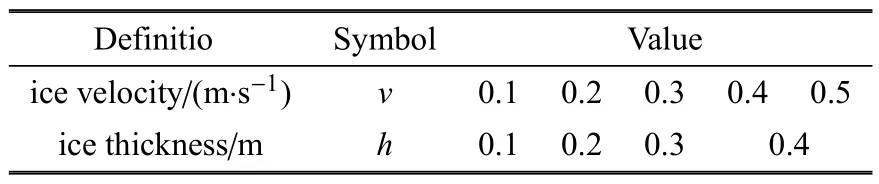
表3 数值模拟中的工况划分Table 3 Working condition of numerical simulation

风机冰激振动的相关计算参数列于表4.当冰速v=0.2 m/s,冰厚h=0.2 m 时，海冰与风机结构相互作用过程如图5 所示.海冰主要与风机锥体上锥作用发生弯曲破坏，破碎冰排发生攀爬与堆积现象，由此引发结构的冰激振动.通过DEM-FEM 耦合方法模拟平整海冰与单桩式风机结构相互作用，可以得到风机承受的冰载荷时程，如图6 所示.该图表明风机冰载荷呈现很强的随机性与周期性.这是由于海冰与风机锥体作用发生弯曲破坏时，破碎冰排与锥体结构会产生周期性的攀爬、堆积和清除，并且冰排攀爬高度和堆积体积表现随机性.由于冰载荷随机性的存在，很难与现场实测数据或者经验公式直接对比，因此本文采取脉冲统计方法[27]，统计数据峰值的均值作为冰载荷时程的冰载荷表征量.

表4 DEM-FEM 模拟中计算参数Table 4 Calculation parameters of DEM-FEM simulation

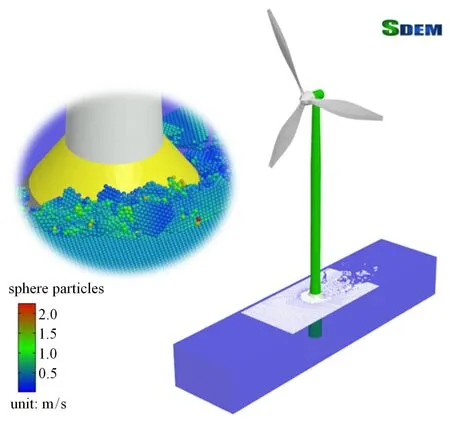
图5 DEM-FEM 模拟海冰与单桩式风机相互作用Fig.5 Interaction between ice and monopile-type wind turbine of DEM-FEM simulation

图6 风机冰载荷时程曲线Fig.6 Time history curve of ice load on the wind turbine

2.2 风机冰载荷验证

为验证模拟结果的准确性，对不同工况下的冰载荷峰值的均值与ISO-19906 标准[28]、IEC6100-3 规范[29]对比.对于带有锥体的单桩式风机结构,两个规范分别给出典型锥体结构的静冰力公式.在IEC6100-3 规范中，采用三维窄结构的的Ralstion 公式，其海冰与正锥体相互作用时冰载荷为[29]

式中，A1，A2，A3和A4为无量纲参数，与海冰与锥体的摩擦系数µ和锥角α 有关；D为水线处锥体直径；DT为锥顶直径，即塔筒直径.

ISO-19906 标准作为世界石油天然气工业领域中寒区海洋结构物设计和评估的行业标准，其基于海冰塑性理论给出平整冰与锥体结构的水平方向冰载荷公式[28]

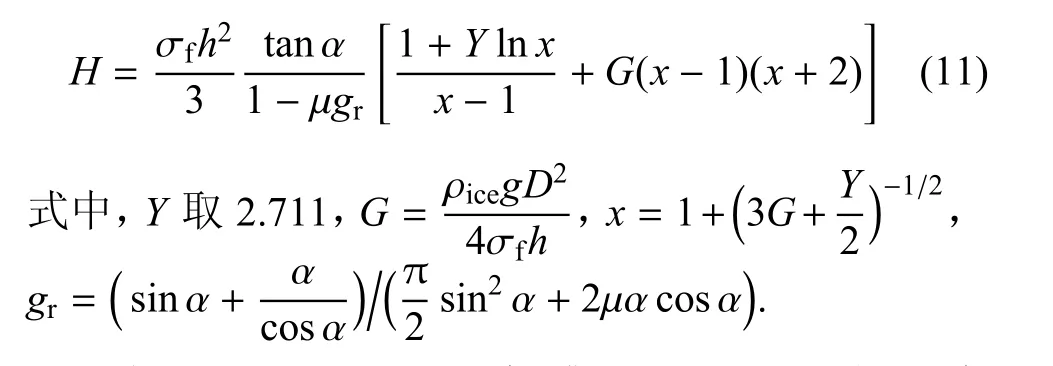
表5 列出ISO-19906 标准和IEC6100-3 规范中经验公式中相关计算参数的具体取值.

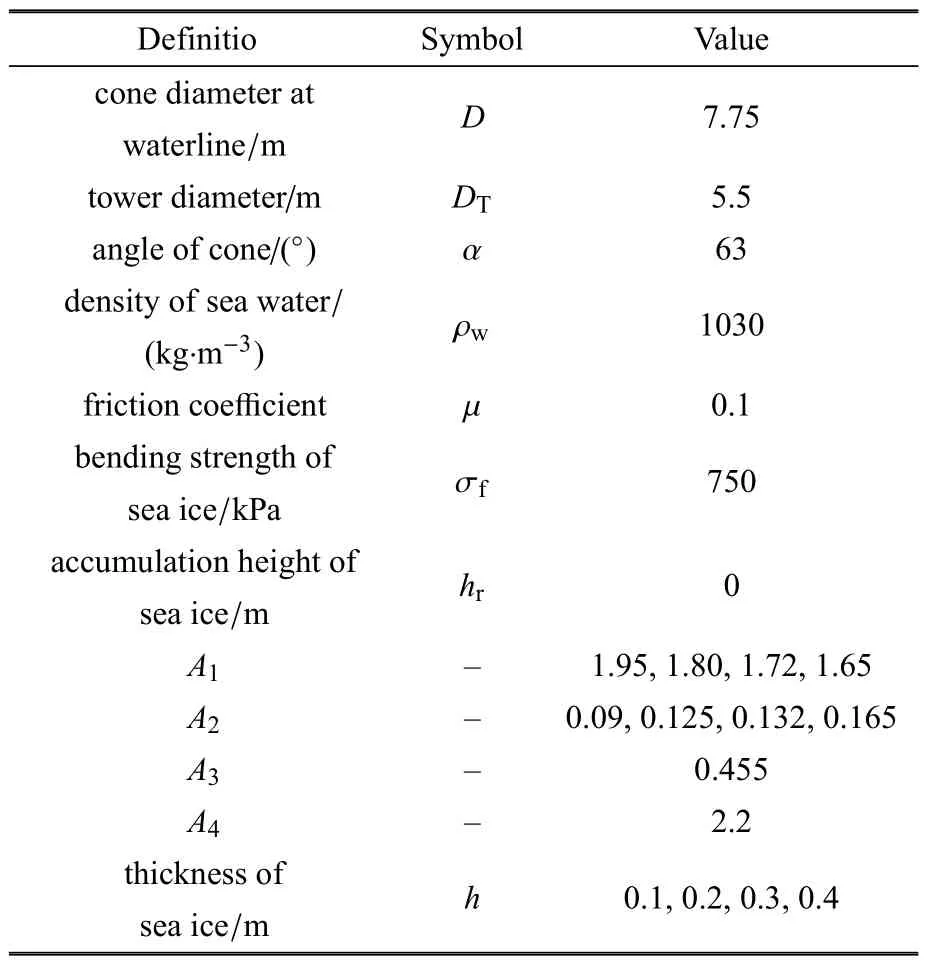
表5 ISO-19906 标准和IEC6100-3 规范锥体结构冰载荷计算参数Table 5 Computational parameters of ice load on conical structure based on codes ISO-19906 and IEC6100-3

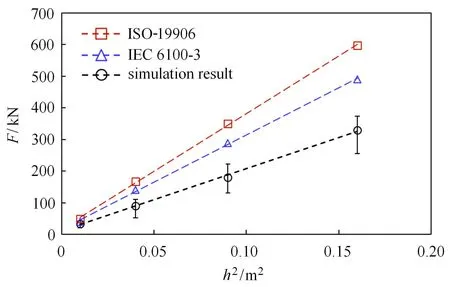
图7 DEM-FEM 计算冰载荷峰值与经验公式对比Fig.7 Comparison between the peck value of ice load in the DEM-FEM simulation and the empirical formulas

图7 所示为DEM-FEM 耦合方法计算的冰载荷峰值的均值与ISO-19906 和IEC6100-3 经验公式对比曲线，其中数值模拟统计的冰载荷为单一冰厚下不同冰速(0.1 ∼0.5 m/s)冰载荷统计表征量的平均值，其具体数值列于表6.三者计算的冰载荷值与冰厚的平方成线性的关系.但是，两个规范公式和DEM 模拟计算结果存在一定的差异.ISO-19906计算的冰载荷结果最大，数值模拟计算的冰载荷最小，并且模拟得到冰载荷由于海冰冰速变化存在着差异.这主要因为DEM-FEM 耦合模型中海冰和结构的宏细观参数选取与经验公式存在一定差异.此外，经验公式更多强调其使用的普遍性，因此其表述结果也相对保守.

表6 DEM-FEM计算方法与经验公式冰载荷计算结果对比Table 6 Calculation results of ice load in the DEM-FEM simulation and the empirical formulas

3 单桩式风机结构的冰激振动响应

为保证风力涡轮机具备最佳的空气动力特性，通常要求结构的动力响应水平被控制在一个很小的水平范围内.因此本文重点关注风电整体结构中基础顶端和塔筒顶端的动力响应能力和动态响应特性.

3.1 单桩式风机结构的位移响应

图8 为冰速0.2 m/s，冰厚0.2 m 工况下塔筒顶端和基础顶端位移响应时程曲线.从图8 可以发现，两者的振动位移时程曲线存在明显的差异：塔筒顶端振动周期T=3.461 s，基础顶点振动周期T=0.708 s.此外，由于冰载荷表现为随机性，使其风机两部分在每个周期的振动幅值也存在明显差别，塔筒顶部的振动幅值范围大于基础顶端的振动幅值.

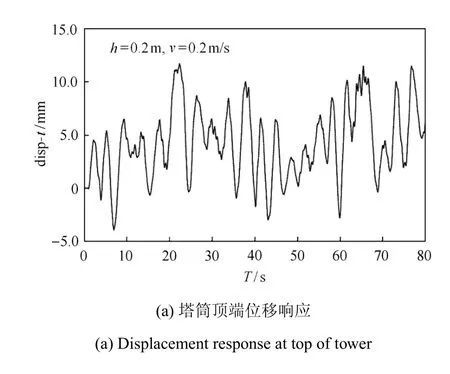
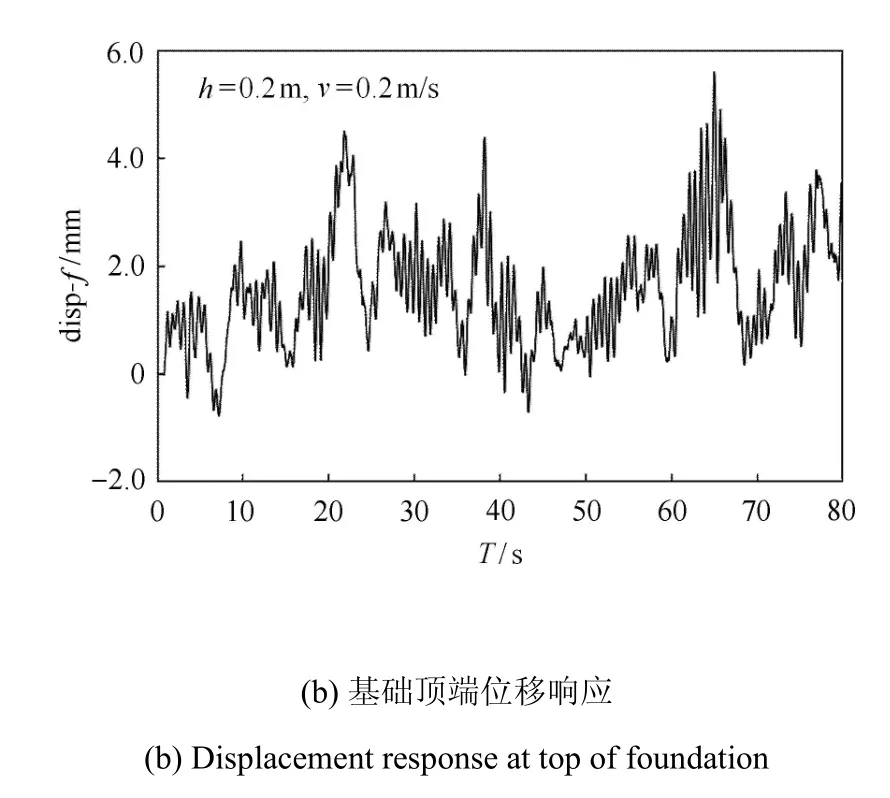
图8 单桩式风机位移响应Fig.8 Displacement response of monopile-type wind turbine

图9 风机结构振动周期Fig.9 Vibration period of wind turbine

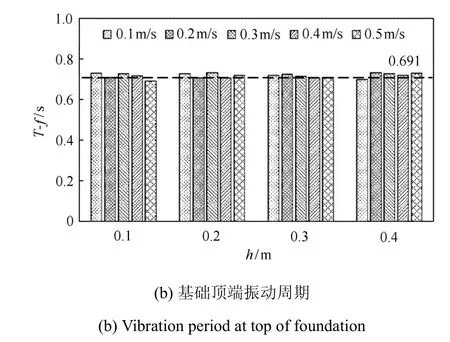
图9 风机结构振动周期(续)Fig.9 Vibration period of wind turbine(continued)

为进一步说明风机塔筒顶端和基础顶端振动周期的差异性，图9(a)为风机塔筒顶端位移振动周期与结构一阶自振周期的对比；图9(b)为风机基础顶端位移振动周期与结构三阶自振周期的对比.结果表明不同的风机部分位移振动特性呈现出差异性：塔筒顶部的振动形式主要以结构的一阶自振周期振动；基础顶端的振动则以结构的三阶自振周期振动.对于安装有抗冰锥体的单桩式风机结构，其各部分在海冰作用下表现出不同动态响应行为，其行为与结构的基础频率密切相关.

为定性描述塔筒顶端和基础顶端在各个工况下的振动幅值，这里引入结构振幅极值A，表示为

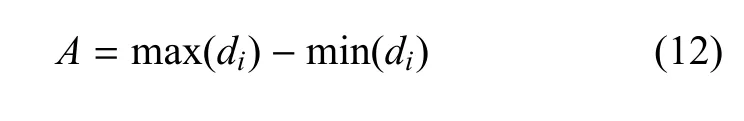
式中，di为第i个位移响应.图10 为风机不同部位结构振幅极值A与冰厚平方的变化关系.对于不同的海冰工况，当冰速一定时，风机各部分结构的振动幅度与冰厚的平方成正相关.

由上述分析可知，塔筒顶端与基础顶端在同一工况下表现出不同的动力敏感特性，因此定义塔筒顶端--基础顶端振幅比γ 来描述动力敏感性的差异[15]，γ 表示为

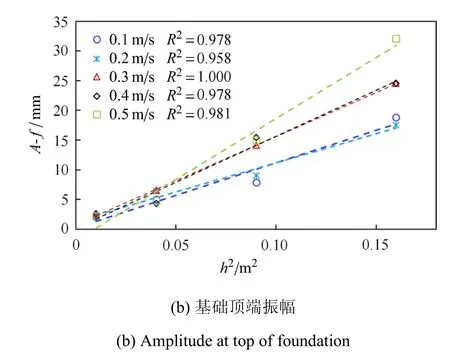
图10 振幅极值与冰厚的关系Fig.10 Relationship between maximum amplitude and ice thickness

式中，Atower为塔筒顶端的振幅极值；Afoundation为基础顶端的振幅极值.图11 为各个工况下γ 取值的分布直方图.可以看出各个工况下，塔筒顶端的振幅与基础顶端的振幅比存在差异，但是变化范围很小(γ 平均值为3.273，方差为0.173).因此，在平整冰与风机锥体基础作用引起的随机振动过程中，由海冰输入的能量主要由风机塔筒上部轮毂、叶片所吸收.通过γ 的分布可以看出，在随机振动模式下，海冰输入能量在风机上下两部分分配变化很小.

图11 不同工况下的风机平均振幅比γFig.11 Average amplitude ratio γ under different working conditions

3.2 单桩式风机结构振动加速度响应

图12 为冰速0.2 m/s，冰厚0.2 m下塔筒顶端和基础顶端振动加速度响应时程曲线.风机两部分结构振动均表现出随机性，符合抗冰锥体结构的振动特点[4,30].

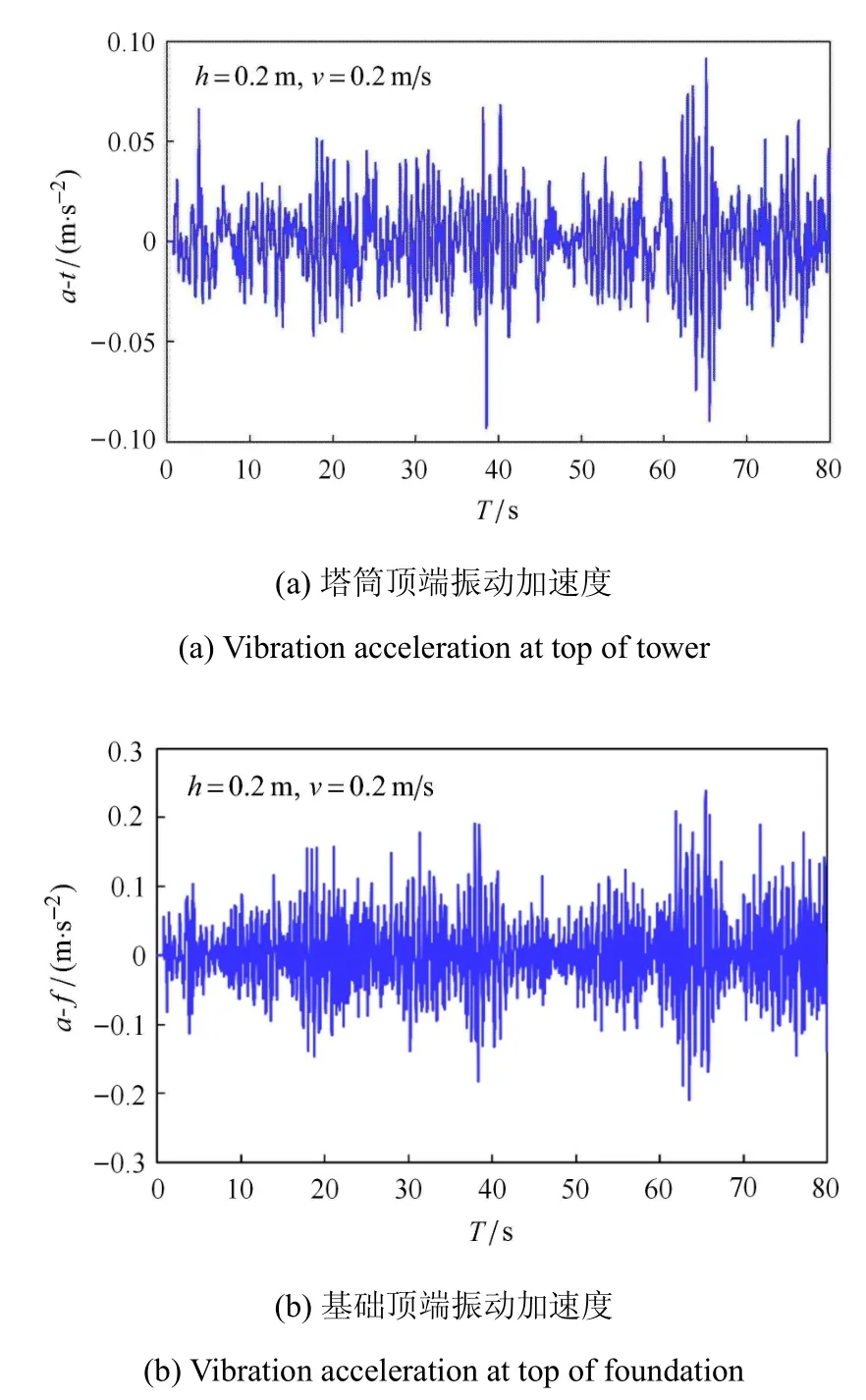
图12 单桩式风机振动响应Fig.12 Vibration response of monopile-type wind turbine

图13 为塔筒顶端和基础顶端振动加速度自功率谱密度曲线.风机两部分结构的频谱分析结果存在很大差异：塔筒顶端的加速度功率谱主要包含3 个频率成分，即0.293 Hz,1.465 Hz 和3.516 Hz，分别对应表2 中风机结构的一、三和五阶自振基频；基础顶端的加速度功率谱则只存在一个频率成分，即1.465 Hz，对应结构的三阶自振频率.此外，风机两部分振动加速度的频域结果显示结构振动的主频主要以结构的三阶自振频率成分为主.

图13 风机振动加速度频谱分析Fig.13 PSD of the ice-inducted vibration acceleration of wind turbine

依据单桩式导管架结构现场原型监测结果，平整冰作用下结构振动加速度响应与冰厚平方和冰速乘积呈线性关系[31]，即

式中，β 为相关系数；amax为振动加速度峰值.图14 为塔顶顶端和基础顶端振动加速度峰值与冰厚、冰速的关系，风机两部分振动加速度响应峰值均与冰厚平方和冰速乘积呈线性关系，两者的相关系数R2分别为0.935,0.854.此外，通过对比两条拟合曲线可知，对于任一工况，风机基础顶端的振动加速度峰值大于塔筒顶端振动加速度峰值，这说明结构各部分振动响应存在着差异，距离海冰与结构相互作用位置越近，其振动响应越剧烈，更容易引起结构疲劳损伤，在后期的风机结构的冰激疲劳分析应重点关注.

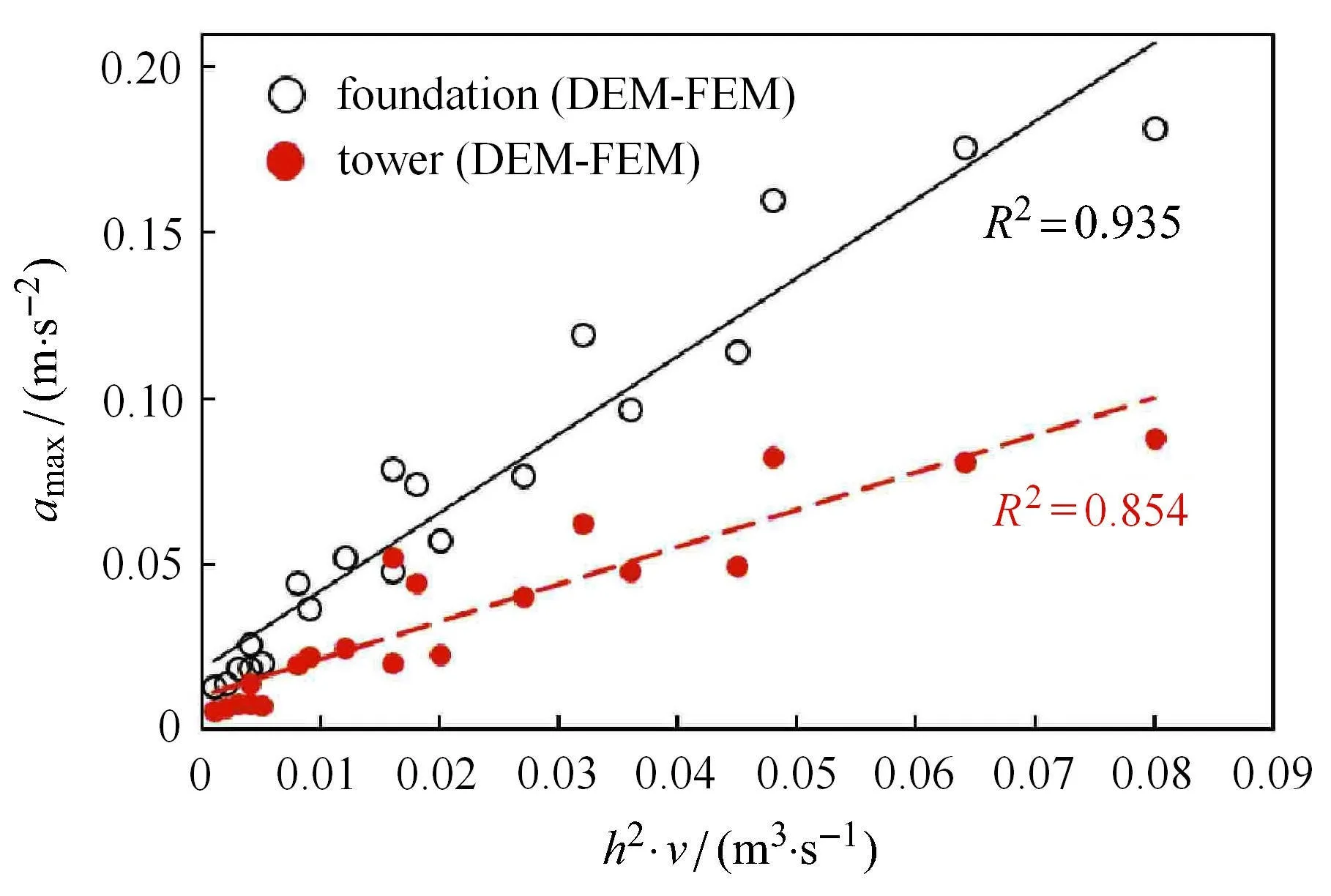
图14 振动加速度峰值与冰速、冰厚的关系Fig.14 Relation between the ice-inducted vibration and ice velocity,ice thickness

通过对风机结构的位移周期和加速度谱分析，在海冰与风机锥体基础结构作用过程中，风机结构的桩基部分以结构的一阶自振频率发生振动.由于海冰断裂长度和攀爬高度的随机性，使得海冰破坏周期没有恒定的值，风机结构产生冰激稳态振动的条件[32]很难出现.因此，海冰破碎作为一种外部激励使得桩基在一阶自振频率持续振动，其振动形式表现为随机振动形式.此外，由于风机结构独有的特点：下部为大刚度桩基和上部为高柔度塔筒，使其动力特征表现为主从式结构特性[15].这种主从式结构特性使得在复杂的冰载荷作用下，风机塔筒(子结构)和桩基(主结构)表现为不同的响应行为，风机不同部位振动周期和加速度谱两者出现差异.

4 结论

本文基于DEM-FEM 耦合模型，采用具有粘结破碎的球形离散单元构造海冰，采用梁单元和三角形板壳单元构造海上单桩式风机结构，模拟风机与平整冰相互作用过程，研究不同冰速、冰厚工况下，风机结构冰载荷特点和结构振动响应能力和行为.研究结果表明，具有抗冰锥体的单桩式风机所承受冰载荷表现一定的随机性与周期性，并且通过与ISO-19906 标准、IEC6100-3 规范中公式对比，验证了本文DEM-FEM 耦合模型计算单桩式风机冰载荷正确性，并得到结构冰载荷与冰厚平方成线性关系；在分析对比不同工况下风机基础顶端和塔筒顶端的位移响应中，通过对两部分振动周期的统计分析发现，塔筒顶部振动周期为结构的一阶自振周期，而基础顶端的振动周期为结构的三阶自振周期.此外，通过引入振幅比，定性地描述结构的动力敏感特性，即塔筒顶端的振幅极值远大于基础顶端振幅极值，两者比值在各个工况中基本不变.这表明由海冰输入的冰力激振能量大部分由风机上部涡轮机吸收耗散，并且能量占比变化很小.在分析对比不同工况下风机基础顶端和塔筒顶端的振动加速度响应中，得到两部分的振动加速度峰值均与冰厚平方和冰速乘积呈线性关系，并且通过对加速度进行谱分析得到风机振动各部分的振动主频为结构的三阶自振频率.此外，由于风机结构的动力特征表现为主从式结构特性，风机不同部位的振动响应行存在很大的差异.综上，基于DEM-FEM耦合模型可为冰区单桩式风机的冰载荷、结构动力行为评估和结构冰激疲劳分析提供有益的数值计算方法，具有很强的工程应用背景.