拟泡-乳曳力模型在大型高温费托流化床反应器中的CFD模拟研究

王 腾，夏梓洪，陈彩霞

(华东理工大学 资源与环境工程学院，上海 200237)

0 引 言

费托合成技术是煤间接液化的核心部分，是煤清洁利用的关键技术之一[1]。根据目标产物的不同及采用的催化剂、反应器形式和反应条件不同，费托合成又可分为低温费托合成和高温费托合成2种工艺[2]。其中高温费托合成工艺在获得大量油品的同时，还可以获得较多的烯烃、含氧化合物等更高附加值的化学品，是未来煤制油行业的重要发展方向之一[3]。气固鼓泡流化床由于其气体和固体颗粒之间传热性能好，床内温度均匀，在高温费托合成反应中具有显著的应用优势[4-5]。

目前，对气固鼓泡流化床中流动、传递和混合过程的研究主要依靠试验完成，诸多关键参数难以直接测量，流场内部特性仍缺乏很好的理解。计算流体力学(CFD)可以得到气固流场的详细信息及其随时间变化的动态行为，已成为流化床反应器开发、设计和放大应用的重要辅助工具。基于双流体模型(TFM)的CFD模拟已经成功预测了气固流化床内的流体力学特性。然而双流体模型基于局部平均的假设，认为单位控制体内气固两相均匀分布，网格必须足够小才能正确揭示介尺度(气泡或颗粒团聚物)的所有细节[6]。对于气固鼓泡流化床，网格尺寸至少需要2～4倍颗粒直径[7-8]。如此细密的网格导致工业级流化床装置的计算量远超现有计算能力。未经修正的粗网格计算又会导致显著的计算误差[9]。因此，应用粗网格模拟大型工业化装置时需要结合非均匀曳力模型对曳力进行修正[10]，以考虑网格尺度内未被解析的局部非均匀结构(或称介尺度结构)对气固流场产生的影响。Wang等[10]采用SGS模型，验证了使用200倍粒径粗网格可以得到与试验结果一致的固含率分布情况。

气泡作为气固鼓泡流化床中最典型的非均匀结构特征，对气固相间曳力具有决定性影响。要建立可靠的非均匀曳力模型，需考虑气泡尺寸对曳力的影响。然而，现有的非均匀曳力模型均是在双流体模型的基础上对传统气固曳力进行修正，以气含率函数的形式体现局部非均匀性对曳力的影响，不能完全反应气泡尺寸的影响。实际上，在气固鼓泡流化床中，气体分别分布于气泡相和乳化相中，气体的不同存在形式使气固相间作用力的作用机制也不同。乳化相内气体和颗粒间通过直接接触的方式作用；气泡与乳化相内颗粒间则通过气泡相和乳化相作用的方式间接作用，且受气泡尺寸的影响。为了描述气泡相与颗粒相之间的曳力，本文提出一种基于欧拉多相流框架的新思路——拟泡-乳三相曳力模型(Pseudo bubble-emulsion triple-phase drag model，PBTD)。PBTD模型将气固鼓泡流化床分为乳化相气体、乳化相颗粒以及气泡三相，分别建立守恒方程，体现气泡的非均匀特性对气固曳力的影响，乳化相内的气固曳力以及气泡相与乳化相内颗粒的曳力分开考虑。

本文采用开发的非均匀曳力模型对大型工业化高温费托流化床反应器进行模拟，考察床层膨胀高度、床层截面气泡和颗粒体积分数的分布规律，研究H2和CO的传质反应速率以及气体组分沿床层高度的分布，并将出口气体组分与试验结果对比，探讨该模型在模拟大型工业化流化床反应器中的适用性。

1 模拟方法

1.1 控制方程

本文采用拟泡-乳三相模型将流化床系统分为气泡相、颗粒相和气相三相，颗粒相和气相组成拟乳化相。气泡相(b)、颗粒相(s)和气相(g)分别采用一套控制方程进行封闭。

质量守恒方程：

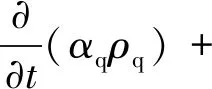
(1)

动量方程：

(2)

(3)

(4)

式中，q为g、b、s相；α为体积分数；ρ为密度；u为速度向量；g为重力加速度；∇·τ为黏性力；α∇p为静压力；∇ps为固相压力；Fg、Fb和Fs为相间作用力项。

应力-应变张量项τq表示为

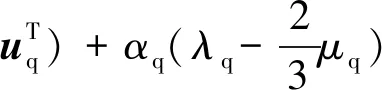
(5)

式中，μq为q相剪切黏度；λq为q相体积黏度；I为单位张量。

颗粒相体积黏度项λS[11]为

(6)

颗粒相剪切黏度μs包括动力部分、碰撞部分和摩擦部分，即

μs=μs,col+μs,kin+μs,fr，

(7)

颗粒相碰撞黏度[12]为

(8)

颗粒相动力黏度[13]为

(9)

颗粒相摩擦黏度[14]为

(10)

颗粒相压力ps方程[11]为

ps=αsρsΘs+2ρs(1+ess)αs2g0,ssΘs，

(11)

其中，ds为颗粒直径；ess为颗粒碰撞弹性恢复系数，取0.9；Θs、g0,ss分别为颗粒温度、径向分布函数；I2D为偏应力张量中的第二不变式；φ为内摩擦角。

径向分布函数[15]为

(12)

式中，αs,max为最大颗粒堆积体积分数。

颗粒温度方程：

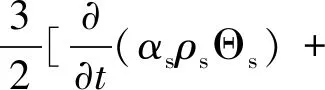
(13)

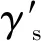
(14)

能量传递项φs计算公式为

φs=-3βgsΘs。

(15)

式中，βgs为气固相间动量交换系数。

1.2 湍流模型

采用混合(Mixture)RNGk-ε模型[16-17]，壁面函数选择标准壁面函数。湍流动能和湍流耗散率控制方程如下：

(16)

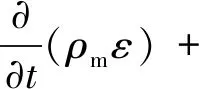
(17)

其中：

(18)

(19)

(20)

(21)

Gk,m=μt,m(∇um+(∇um)T)∶∇um，

(22)

式中，ρm为混合密度；μm为分子黏性，um为混合速度；μt,m为湍流黏度；Gk,m为湍动能产生项；αq、ρq、μq、uq分别为q相的体积分数、密度、黏度和速度；Cμ、C1ε、C2ε为湍流模型参数；σk、σε为湍流动能k和湍流耗散率ε的湍流普朗特数。

1.3 曳力模型

气固流化床中，气固两相密度相差很大，其他作用力对气固流场的影响有限，可忽略不计，只考虑曳力的作用。由于采用了三相假设，原则上会出现3组相间曳力：气泡-颗粒曳力、气泡-乳化相气体曳力以及乳化相内气体-颗粒曳力。本文在模型推导过程中，将颗粒相和气相看作“拟乳化相”，考虑气泡与拟乳化相之间的曳力，并最终将该曳力体现在颗粒和气泡的动量方程中。在计算气泡-拟乳化相曳力时采用拟乳化相的密度和黏度，以考虑乳化相中气体的存在对气泡和乳化相之间作用力的影响。因此式(2)～(4)中相间作用力项可表示为

Fg=βg-s(ug-us)，

(23)

Fb=βb-s(ub-us)，

(24)

Fs=βb-s(ub-us)+βg-s(ug-us)，

(25)

式中，βg-s、βb-s分别为乳化相内气体-颗粒动量交换系数、气泡-颗粒动量交换系数。

在考虑气泡与乳化相颗粒相间曳力时，乳化相为连续相，气泡为离散相。根据牛顿第二定律，乳化相对气泡相的曳力等于气泡相对乳化相的曳力，因此根据通用曳力公式，在单位控制体积内，单个气泡对拟乳化相曳力的表达式为

(26)

其中，CDb为气泡群曳力系数；ρe为拟乳化相密度；Uslip,i为相间表观滑移速度，Uslip,i=(ub-ue)(1-αb)。由此可得，单位控制体内，所有气泡与拟乳化相之间的曳力为

(27)

根据A类双流体模型曳力系数公式[13]，气泡-拟乳化相之间的相间动量交换系数可表示为

(28)

式中，αe为乳化相体积分数；ue为乳化相速度。

由于在PBTD模型中，气泡-拟乳化相曳力最终反映在颗粒相的动量方程中。因此将式(28)中的ub替换为us。气泡相与颗粒相之间的等效相间动量交换系数为

(29)

采用Ishii和Zuber[18]提出的公式，即

CDb=CDb0(1-αb)-0.5，

(30)

式中，CDb0为单气泡曳力系数，由Darton和Harrison[19]关系式计算所得。

(31)

(32)

其中，Reb为气泡雷诺数；db为气泡直径；μe为拟乳化黏度。

db采用Mori和Wen[20]提出的经验公式，即

(33)

db0=0.003 76(u0-umf)2,

(34)

式中，dbm为最大气泡直径；db0为初始气泡直径；h为床层高度；Dt为床层直径；u0为入口气速；umf为最小流态化气速。

本文模拟所用反应器内置大量冷却盘管，内构件的存在会对气固流体动力学特征产生影响，其复杂程度也高于空塔流化床反应器。Ozawa等[21]发现在带有竖直列管的气固流化床中，A类颗粒和B类颗粒床层内部气泡仍符合随着床层的升高气泡尺寸逐渐增大，但受内构件的影响，平均气泡尺寸均小于Mori-Wen关系式预测值。Ozawa等根据列管的影响，对Mori-Wen气泡尺寸公式中的最大气泡尺寸进行修正，提出以下最大气泡尺寸修正公式：

dbm=0.59[DtHt(u0-umf)]0.4，

(35)

式中，Ht为列管中轴线距离。

拟乳化相密度ρe和黏度μe受气体和固体颗粒浓度的共同影响，密度通过拟乳化相内部气固两相体积加权平均求得，黏度计算采用Ishii和Zuber[16]的经验公式，具体为

ρe=ρs(1-αeg)+ρgαeg，

(36)

μe=μg(1-αes/αs,max)-2.5αs,max，

(37)

其中，as,max为乳化相中最大颗粒堆积密度，取0.63；αeg和αes分别为乳化相中相对气含率和固含率，计算公式为

(38)

αes=1-αeg。

(39)

拟乳化相内的气固相间作用力采用传统Gidaspow曳力模型[12]，需要注意的是，方程中的气固体积分数采用拟乳化相内的相对体积分数，相间动量交换系数βg-s表达为

(40)

(41)

CD=0.44(Res>1 000)，

(42)

(43)

1.4 传质模型

基于拟泡-乳三相曳力模型的假设，相间传质存在于气泡相与拟乳化气相之间，该相间质量传递主要由气流穿流项和扩散项两部分组成。Sit和Grace[22]认为在细小颗粒的流化床中，扩散速率是相间质量传递速率的控制因素，而在粗颗粒流化床中，气流穿流是相间传递速率的决定性因素。Kunii和Levenspiel[23]将气泡与乳化相之间的质量传递过程分为2个步骤：首先气体通过气泡传递到气泡晕；其次再从气泡晕传递到乳化相中。并分别用2个交换系数Kbc和Kce的综合表示气泡与乳化相之间的交换总系数Kbe。本文采用Kunii和Levenspiel提出的质量传递模型描述气泡与拟乳化相之间的质量传递并忽略气泡晕相，认为气泡与气泡晕之间的质量交换系数Kbe等于气泡与拟乳化相之间的质量传递系数，表达式为

(44)

其中，Dg为气体扩散系数。等号右侧第1项为气体穿过气泡而引起的质量交换，即穿流贡献项(through-flow contribution)，第2项为扩散引起的质量交换，即扩散贡献项(diffusion contribution)。

除了气泡和乳化相之间的传质，乳化相内中气体混合物之间也存在扩散现象。对于多组分气体中的扩散，组分i在混合物中的质量扩散系数Di,m可表示为

(45)

其中，Xi为组分i的摩尔分数；Di,j为双组分体系的分子扩散系数，其计算公式为

(46)

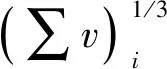
1.5 反应动力学模型

F-T合成反应是一个多种反应并存的复杂反应体系，具有众多的主反应和副反应，其发生的概率随催化剂种类和操作条件的不同而变化[24]。主反应主要生成烷烃类和烯烃类产物，副反应包括水煤气转化(Water gas shift，WGS)反应以及生成含氧化合物的反应。

主反应为：

(47)

副反应为：

(48)

(49)

关于F-T合成反应的动力学，学者进行了深入广泛的研究。目前最常用的是考虑合成气消耗速率的气体消耗动力学模型[25-29]。本文采用某公司通过试验测量数据拟合的动力学模型，具体为

(50)

(51)

其中，RFT、RWGS分别为费托反应和水煤气变换反应速率系数，kmol/(m3·s)；kft、Eft、k1、kwgs、Ewgs为常数，取值分别为：kft=0.003 224 6，Eft=46 239，k1=0.029，kwgs=1.54，Ewgs=7 392。Keq=0.012exp(4 630/T)；P(H2)、P(CO)、P(H2O)分别为H2、CO和H2O的气相分压；R为通用气体常数，取8.314 5 J/(K·mol)。

F-T合成反应除生成烃类产物外还生成相当数量的含氧有机物，两者相对选择性是一定值，其中含氧有机物选择性XCHO为

(52)

其中，m为试验测得的摩尔流率；prod为出口气体；feed为入口气体。由于高温费托合成的含氧有机物组分复杂，模型采用含量最高的乙醇代表含氧有机物。

1.6 反应器几何模型及计算条件

计算几何模型基于某公司开发的4 500 t/a中试规模高温费托流化床反应器装置，如图1所示(L为冷却盘管长度，D为反应器直径，D′为冷却盘管直径)。反应器高度为24 000 mm，直径为900 mm。内部冷却盘管外径为90 mm，高度为7 000 mm。

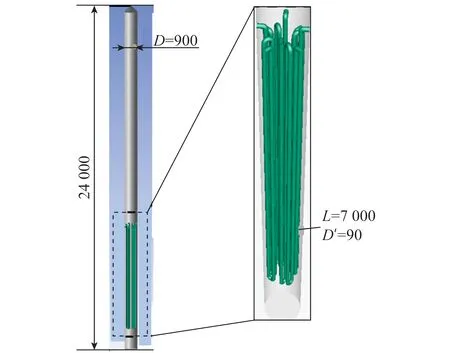
图1 高温费托流化床反应器结构示意

采用六面体结构化网格对几何模型进行网格划分，网格数量约为88万，属于平均尺寸约为600倍颗粒直径的粗网格。为了捕捉壁面对流场的影响，网格在管壁附近进行了局部加密处理，如图2所示。

图2 中试规模高温费托流化床网格

模拟时气相和气泡相采用均匀进气，进气速度U0=0.495 m/s。由于催化剂所用颗粒为Geldart A类颗粒，因此气相进口表观速度为最小鼓泡速度Umb，为0.007 2 m/s，气泡相进口表观速度为(U0-Umb)。入口边界湍流强度为5%，水力直径采用几何直径。气相采用无滑移(no-slip)的边界条件，气泡相壁面采用自由滑移，颗粒相壁面采用部分滑移(partial slip)，其中镜面系数(specularity coefficient)设置为0.05[30]，颗粒碰撞恢复系数设置为0.9[31]。相间作用力模型和气泡尺寸模型通过用户自定义函数(User defined function，UDF)并耦合到Fluent模拟计算。所用时间步长设置为0.001 s，每个时间步长迭代20步。模拟时间总长为100 s，对50～100 s模拟瞬时结果进行数据采集并进行时均处理。

模拟采用的物性参数见表1。试验测得床层内部温度基本均匀，因此本文假设床内温度均匀，不存在温度梯度，模拟不涉及床层与冷却盘管传热，只考虑冷却盘管对气固流场的影响。

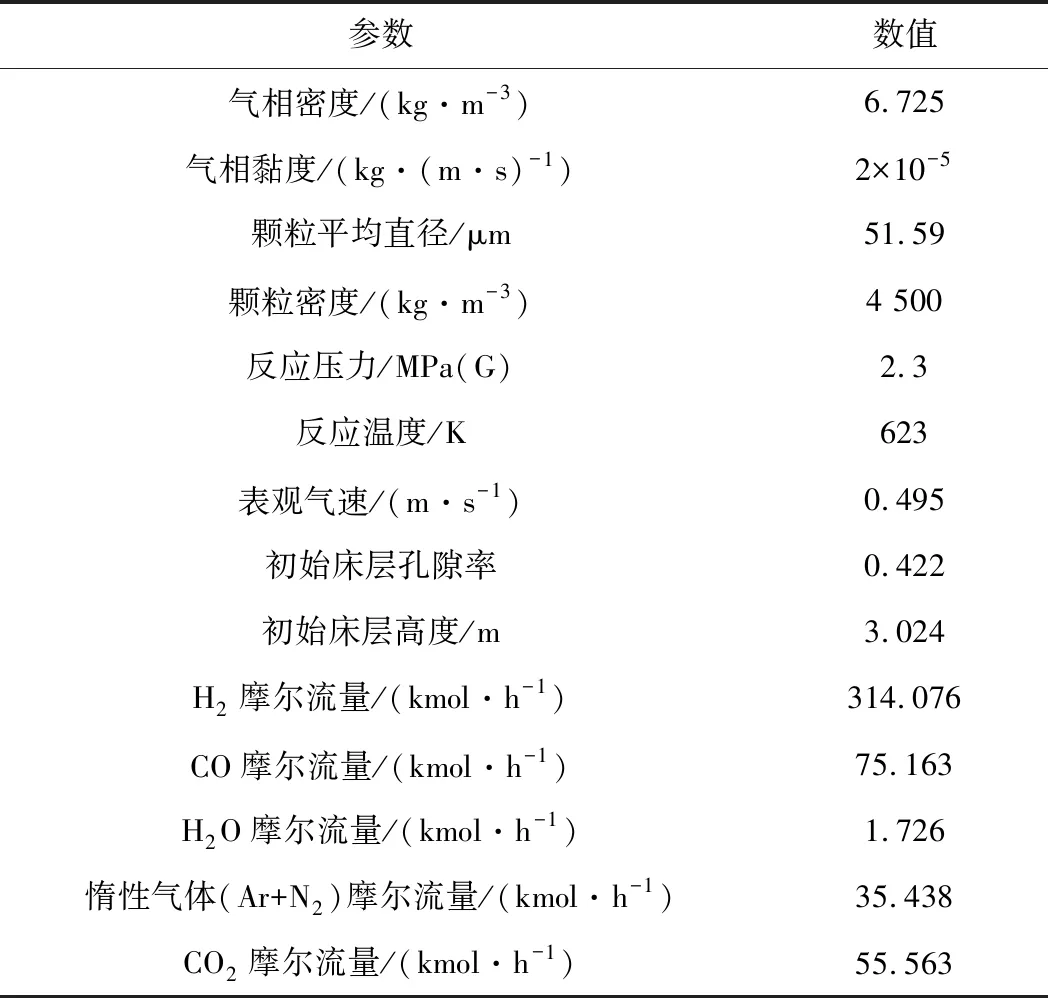
表1 模拟参数

2 结果分析与讨论

2.1 总体流化状态

图3为采用非均匀曳力模型时模拟的床层膨胀高度情况，可以看出，床层稳定时床层高度为初始床层高度的2倍左右。根据Cloete[32]提出的床层膨胀高度判据：床层膨胀高度应该在固含率0.05的位置，模拟所得床层最终膨胀高度为8.2 m。由于中试装置处于高温高压的恶劣环境，无法进行试验测量，本文采用Cai等[33]提出的经验公式(53)计算床层膨胀高度，该经验公式适用于计算高温高压条件下气固流化床的床层膨胀高度。经计算，床层膨胀高度约为8.1 m，模拟床层膨胀高度和经验公式预测值的相对误差为1.2%，PBTD曳力模型能够在粗网格条件下较好地预测床层的膨胀情况。

(53)

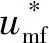
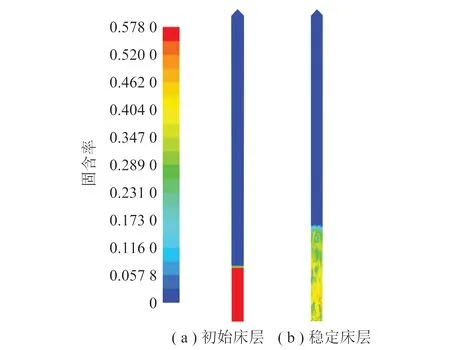
图3 流化床床层固含率分布

2.2 床层时均相含率分布

床层不同高度处的时均气泡体积分数和固体颗粒体积分数分布云图如图4、5所示。可知冷却盘管管壁附近，气泡的体积分数明显高于其他部分，固含率则相反，管壁附近固含率低于其他部分，说明气泡趋于沿着冷却盘管管壁上升，这与Rudisuli等[34-35]的试验现象一致。在流化床壁面，气泡体积分数降低，颗粒体积分数升高，这主要是由于颗粒到达流化床床层表面后，气泡离开床层，颗粒沿壁面下降。表明有内构件存在的流化床仍然具有固体颗粒浓度边壁浓、中心稀的非均匀分布特点。随着高度的增加，床层截面气泡平均体积分数逐渐增大，颗粒平均体积分数逐渐下降，符合流化床颗粒浓度下浓上稀的总体非均匀特性。

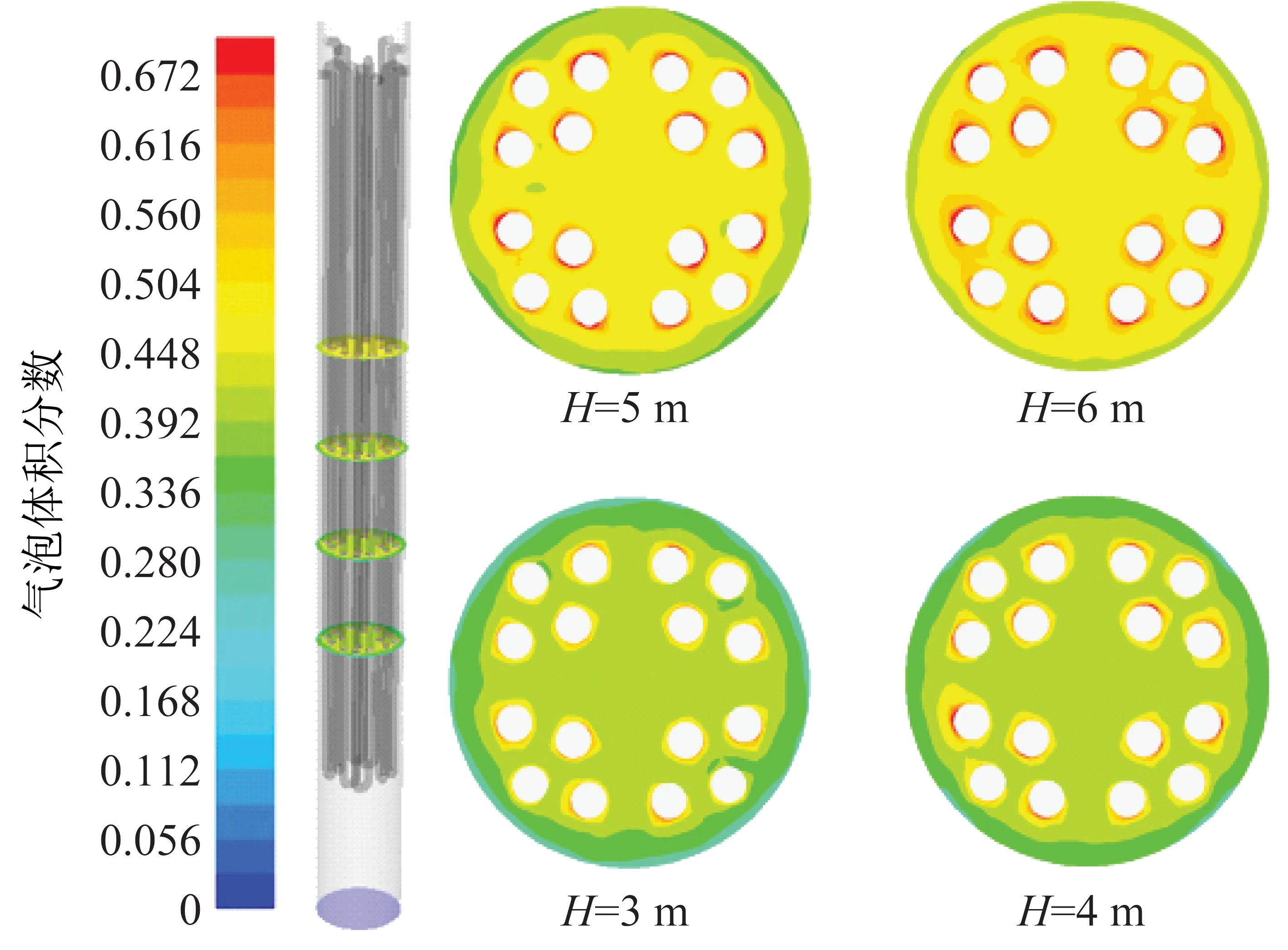
图4 不同床层高度处时均气泡体积分数分布云图

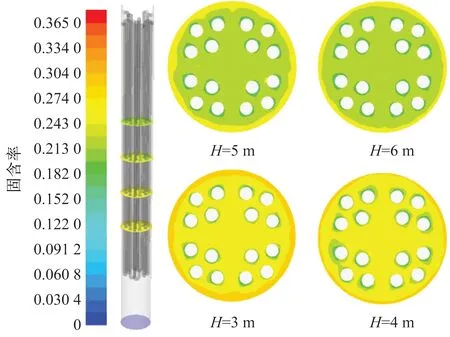
图5 不同床层高度处时均固含率分布云图

2.3 传质速率及各组分浓度分布

合成气的传质速率分布云图和费托反应速率分布云图如图6、7所示。可知，CO传质速率≈H2传质速率/2，与反应方程中的化学计量比一致。由图中还可以看到，伴随着反应器高度的增加，反应不断进行，CO和H2的传质速率和F-T反应的反应速率都呈逐渐减弱的趋势。

图6 H2和CO的传质速率分布

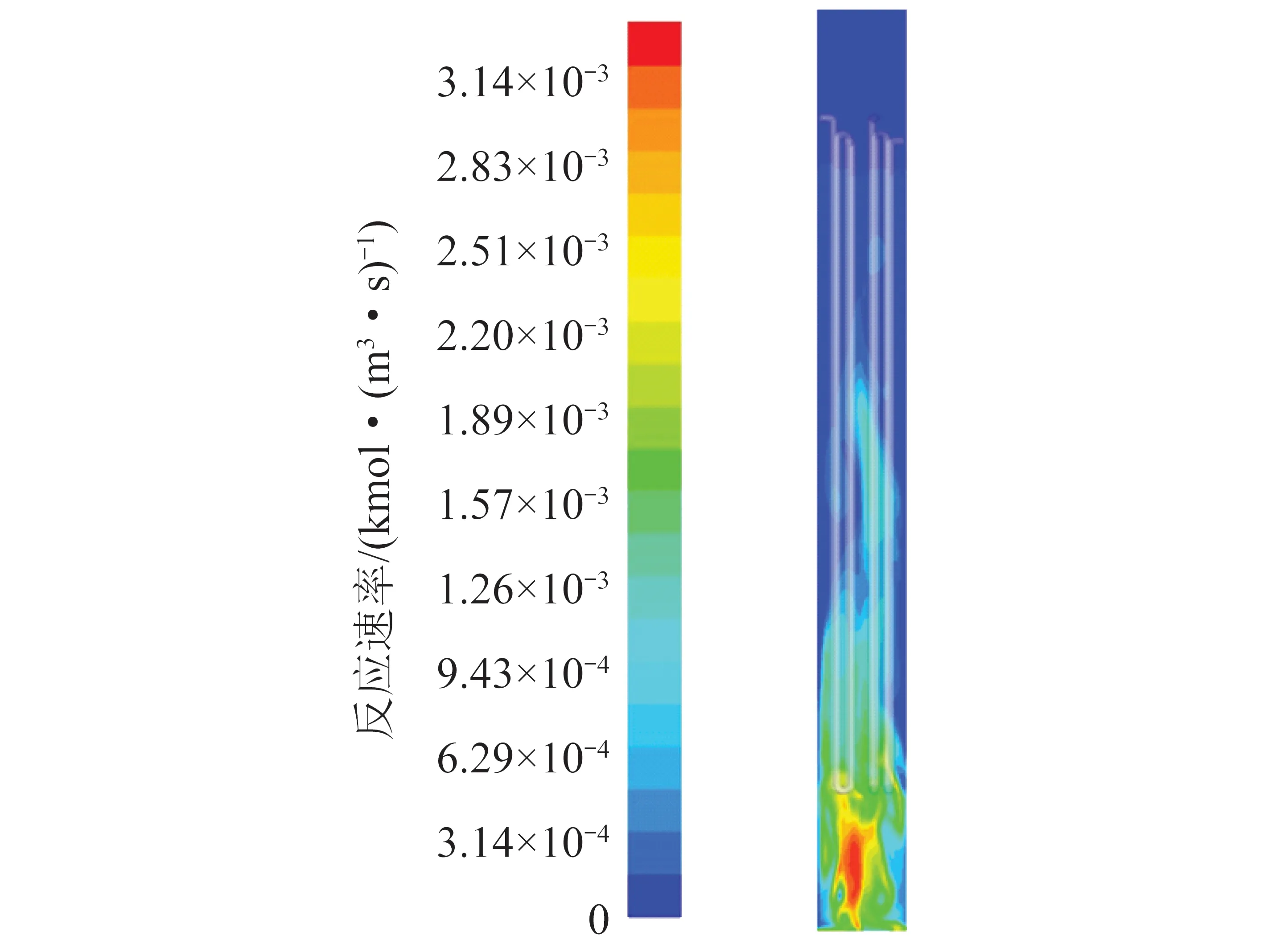
图7 费托合成反应速率分布

床层内部气体成分(CO、H2、[—CH2—]、C2H5OH、H2O、CO2)时均质量分数随流化床床层高度的变化如图8所示。可知随着F-T反应的进行，CO和H2被大量消耗，其含量随床层高度的升高迅速降低。反应生成产物[—CH2—]、C2H5OH、CO2、H2O随着床层高度的升高逐渐增加。床层1.6 m附近，组分曲线明显出现一次明显波折，随后气体组分反应速率变缓慢。这是由于1.6 m后床层开始出现冷却盘管，使气固流场发生明显改变，气泡沿管壁上升，气体传质速率降低，因此反应速率随之降低。

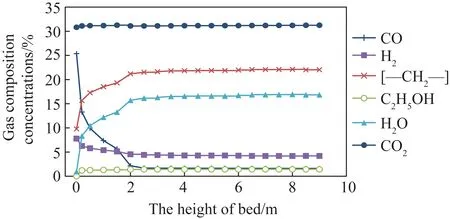
图8 气体组分浓度沿床层高度的分布

反应器出口气体组分质量分数与试验测量数据对比如图9所示，可知主要产物气体组分质量分数的模拟值与试验值之间比较接近，主要生成产物(H2O、CO2、C2H5OH和[—CH2—])质量分数相对误差在1.5%～16.0%，表明PBTD模型基本适用于工业规模的反应器模拟。

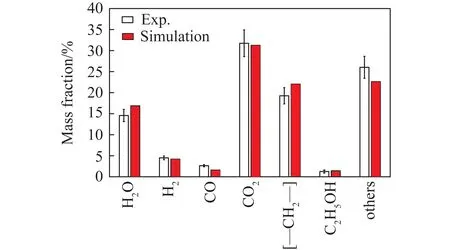
图9 反应器出口气体组分浓度

3 结 论

1)采用PBTD模型结合Ozawa等提出的气泡尺寸模型，在粗网格条件下对反应器进行模拟，得到的床层膨胀高度与文献公式预测值的相对误差为1.2%。PBTD模型能够呈现气泡趋于沿着内构件管壁上升的运动规律，发现有内构件的气固流化床仍然具有颗粒浓度下浓上稀、边壁浓中心稀的宏观非均匀特性。

2)CO传质速率约为H2传质速率的1/2，与反应方程中的化学计量数一致。模拟结果显示，随着反应进行，CO和H2传质和反应速率逐渐降低。

3)冷却盘管的存在影响气固混合效率，从而影响反应速率。模拟出口主要产物气体组分(H2O、CO2、C2H5OH和[—CH2—])质量分数与试验测量值相对误差在1.5%～16.0%，表明本文开发的基于非均匀假设的PBTD模型适用于模拟工业规模的反应器，为大型工业化流化床反应器提供了实用的模拟方案。