基于OpenFOAM的挡板透空式防波堤水动力特性数值分析

王国玉，顾新红，秦世杰，于 明，张恩铭

(1.大连理工大学海岸和近海工程国家重点试验室，辽宁 大连 116024;2.山东港通工程管理咨询有限公司， 山东 烟台 264000)

近年来，随着人们对海洋生态环境的重视，防波堤除了要抵御外海波浪、形成一个供船舶停靠作业的掩蔽水域外，还需具有实现港内外海水交换、发展生态渔业和休闲观光等功能。因此，桩基挡板式透空防波堤越来越受到研究者和工程界的关注。

Ursell[1]于1947年首先理论分析了无限水深情况下直立薄板防波堤的透射系数与反射系数。Weigel[2]于1960利用微幅波理论推导了有限水深情况下直立薄板防波堤透反射系数的解析解。国内关于透空式防波堤的研究始于1986年，邱大洪等[3]在假定波浪遇结构物发生绕射的前提下，推导了任意水深下透射系数与反射系数的解析解，计算结果与理论值和试验值吻合较好，为透空式防波堤的研究奠定了基础。王国玉等[4]利用理论分析方法对T型透空式防波堤进行了研究，发现水平板的潜深和竖直板的高度对其消波性能有较大影响。严以新等[5]利用断面模型试验，对多层挡板桩基透空堤消浪特性进行了试验研究，得出了影响波浪透射率的主要因素，并证明了该种结构可以建于水深浪大潮差大的海区。钟瑚穗等[6]对小间距直桩式、栅栏式和直立挡板式透空堤开展物理模型试验研究，对比了3种模型的透射系数，并提出了消浪效果较好的新型组合式透空堤。王国玉等[7-8]提出了一种多层水平板式防波堤结构，并通过物理模型试验、理论分析等方法重点研究了影响其消浪性能的因素。Laju等[9]设计了一种带有双侧挡板的桩基式透空堤，分别应用特征函数展开法和物理模型试验得到了结构的透射系数，并证明了该结构物适用于深海。Shin等[10]通过将理论值与试验值对比，分析了板间距、吃水深度对双垂板透反射系数的影响，结果表明，当两板间距一定时，随着板的相对入水深度增大，结构物的反射系数增大，透射系数减小，同时也研究了板间的液面振荡问题。程永舟等[11]研究了上下层平板相对间距以及格栅板间隙比等参数对防波堤透射系数和反射系数的影响。Alsaydalani 等[12]研究了三块竖直板防波堤与波浪作用后的反射、透射、能量损耗、波浪力等水动力特性。

现有关于挡板式透空防波堤的文献研究结果表明，学者们主要集中于对防波堤透射系数和反射系数的研究，而对于挡板周围流场的研究工作相对缺乏。特别是在追求较佳的掩护效果时，挡板往往入水深度较大，此时挡板底部海床表面的流速是工程人员关注的主要问题之一。因此，开展透空式防波堤底部流速的分析工作，将对挡板透空式防波堤的优化设计以及减缓防波堤底部海床的冲刷具有重要的参考价值。

1 数学模型

二维数值波浪水槽的建立是基于开源CFD软件OpenFOAM。流体控制方程的离散采用有限体积法，该方法可灵活地运用结构化网格和非结构化网格，便于模拟具有复杂边界形状结构物周围的流体运动。

1.1 控制方程

不可压缩黏性流体的运动应遵循如下连续性方程和动量方程：

(1)

(2)

式中：ui为流体质点在3个方向上的速度分量；ρ为密度；t为时间；p为压强；gi为重力加速度；μe为有效动力黏性系数。

1.2 边界条件

1.2.1自由水面条件

VOF方法是追踪自由液面的一个有效途径，其基本思想是，在整个流场中定义一种流体体积与网格体积比值α的函数，其中α=1处的网格充满该流体，α=0处的网格则不含有该流体，在0<α<1的网格区域含有自由面。体积分数α需满足输运方程[13]：

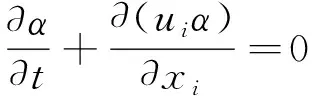
(3)

为避免自由液面附近出现两相流界面模糊不清的问题，OpenFOAM对上述输运方程进行了修正，通过添加人工压缩项来提高体积分数α的计算精度，修正后的方程为

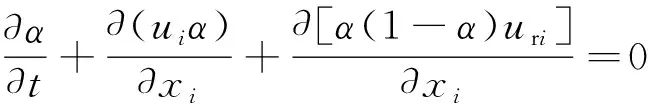
(4)

式中：uri为垂直于两相流界面的速度分量。

1.2.2造波、消波边界

造波边界波浪的产生方法为，依据Stokes 5阶波浪理论，在造波边界直接给出随时间变化的自由表面高程和流体质点速度分布，生成目标规则波浪。水槽左侧造波端设置一定厚度的海绵层，其作用为稳定造波边界产生的波浪并消除波浪二次反射的影响；类似的，水槽右侧尾端设置一定厚度的海绵层，其作用为吸收向右传播的波浪从而消除水槽尾端壁面产生的反射波浪。数值海绵层[14]的基本思想是，在每一个计算时间步长内将自由水面高程η、流体质点速度u从计算值修正至目标值，修正的公式如下：

φ=αRφcomputed+(1-αR)φtarget

(5)

式中：φ为需要被修正的物理量；φcomputed为由控制方程求出未经修正的计算值；φtarget为目标值；αR为修正权重，其在海绵层区域内的分布用如下公式计算：

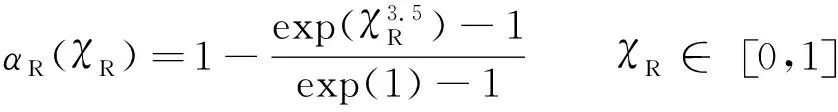
(6)

式中：χR为网格单元在海绵层内的相对水平位置。

αR与χR的关系如图1所示。可以看出，在海绵层区域内，αR平滑的由0过渡到1，可以保证计算值的修正平滑进行。

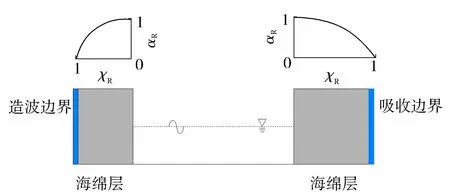
图1 消波区αR(χR)变化示意图

1.3 控制方程的离散及求解

数值计算采用有限体积法进行，将计算区域划分成一系列控制体积，再通过守恒型控制方程对控制体积做积分来导出一组离散方程，各项数值积分通过插值来计算。OpenFOAM提供了多种插值格式供选择。本文所采用的插值格式如表1所示。压力、速度耦合方程采用压力的隐式算子分割算法(pressure implicit with splitting of operators， PISO)进行求解。

表1 插值格式

2 数值波浪水槽

2.1 数值水槽建立

为了验证上述数学模型，在大连理工大学海岸和近海工程实验室的海洋环境波浪水槽(50.0 m×3.0 m×1.0 m)中，笔者设计并完成了规则波与桩基挡板透空式防波堤作用的物理模型试验(图2)。试验水深为0.25 m，入射波高为0.04 m和0.08 m，对应的波浪周期分别为0.91 s、1.10 s、1.28 s、1.46 s和1.64 s。结构物布置在距离造波板27.0 m处，前侧挡板入水深度为0.2 m，流速仪布置在挡板前沿处，流速测点位置在挡板下方距离水槽底部0.02 m位置处。试验中布置了5个浪高仪G1～G5用来观测结构后方的波面历时，第一个浪高仪布置在距离结构物后方1.35 m处，相邻两个浪高仪间距为0.50 m。在挡板的迎浪侧设置了5个波浪压力测点，测点位置如图3所示。

图2 挡板透空式防波堤模型试验布置(单位：m)

图3 物理模型试验压力测点布置示意图(单位：mm)

图4给出了基于OpenFOAM建立的二维数值波浪水槽。水槽长度取为15.0 m，结构物放在距造波板6.0 m处，距左端约3～5倍波长。波面、流速和波压力测点位置与物理模型试验中保持一致。水槽左端造波边界位置处设置了一个宽度为2.0 m的海绵层，用来吸收由结构物产生的反射波浪，从而消除数值波浪水槽中的波浪二次反射问题。类似的，水槽右侧吸收边界位置处设置了一个宽度为3.0 m的海绵层，用来吸收向右传播的波浪。

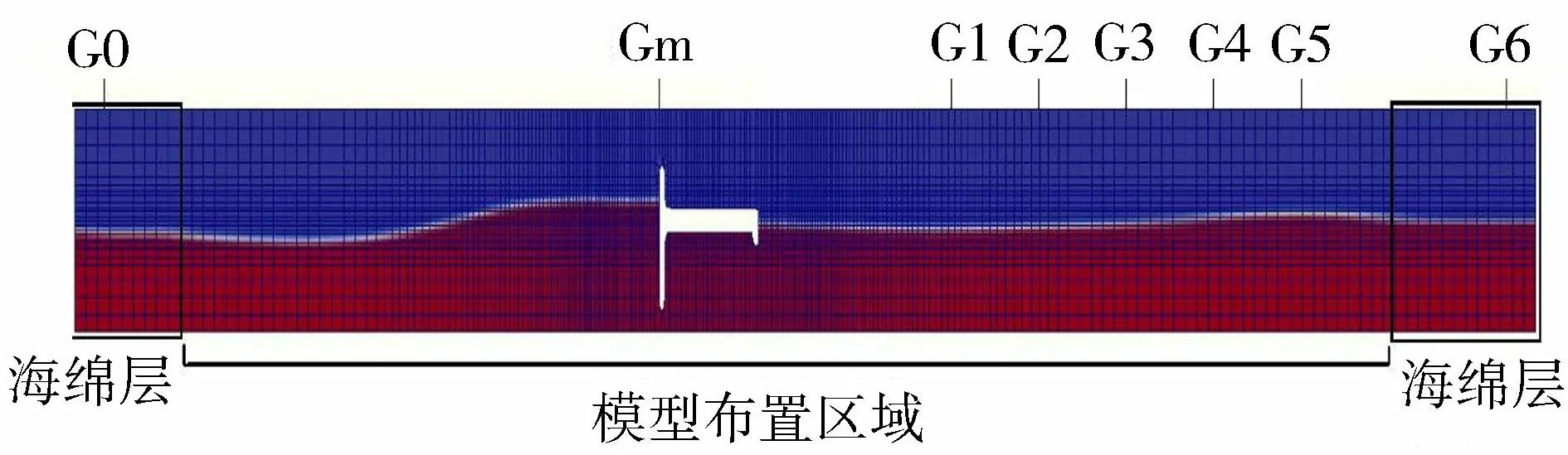
图4 数值水槽计算域布置示意图(单位：m)

兼顾计算精度与时间，经过一系列网格收敛性验证，背景网格的剖分依据如下[15]：波长范围内100个网格，波高范围内10个网格，并对波面附近及结构物周围进行了网格局部加密，以提高波面信息的捕捉精度。时间步长的控制因素主要为Courant数，表示一个时间步长内允许流体质点穿过的网格数量，Courant数越大，步长越大，计算收敛的速度越快。本文中最大Courant数设置为0.25，并设置允许时间步长根据Courant数进行调节。

图5为水槽中未布置结构物(空水槽)时，左侧造波边界处海绵层内G0处、右侧吸收边界海绵层内部G6处和放置模型的位置Gm处3点在入射波浪的波高H=0.08 m和周期T=1.46 s时的波面η历时过程。G0处的波高几乎不发生变化，说明造波边界处的海绵层可以很好地消除波浪的二次反射作用。同样的，G6处的波高几乎为0，这表明右侧吸收边界处的海绵层能够有效地吸收向右传播的波浪。而结构物处Gm点的波面过程线分布均匀，波高随时间衰减的相对误差在2%以内。

图5 空水槽各测点波面历时曲线(H=0.08 m，T=1.46 s)

2.2 数值水槽验证

2.2.1波面验证

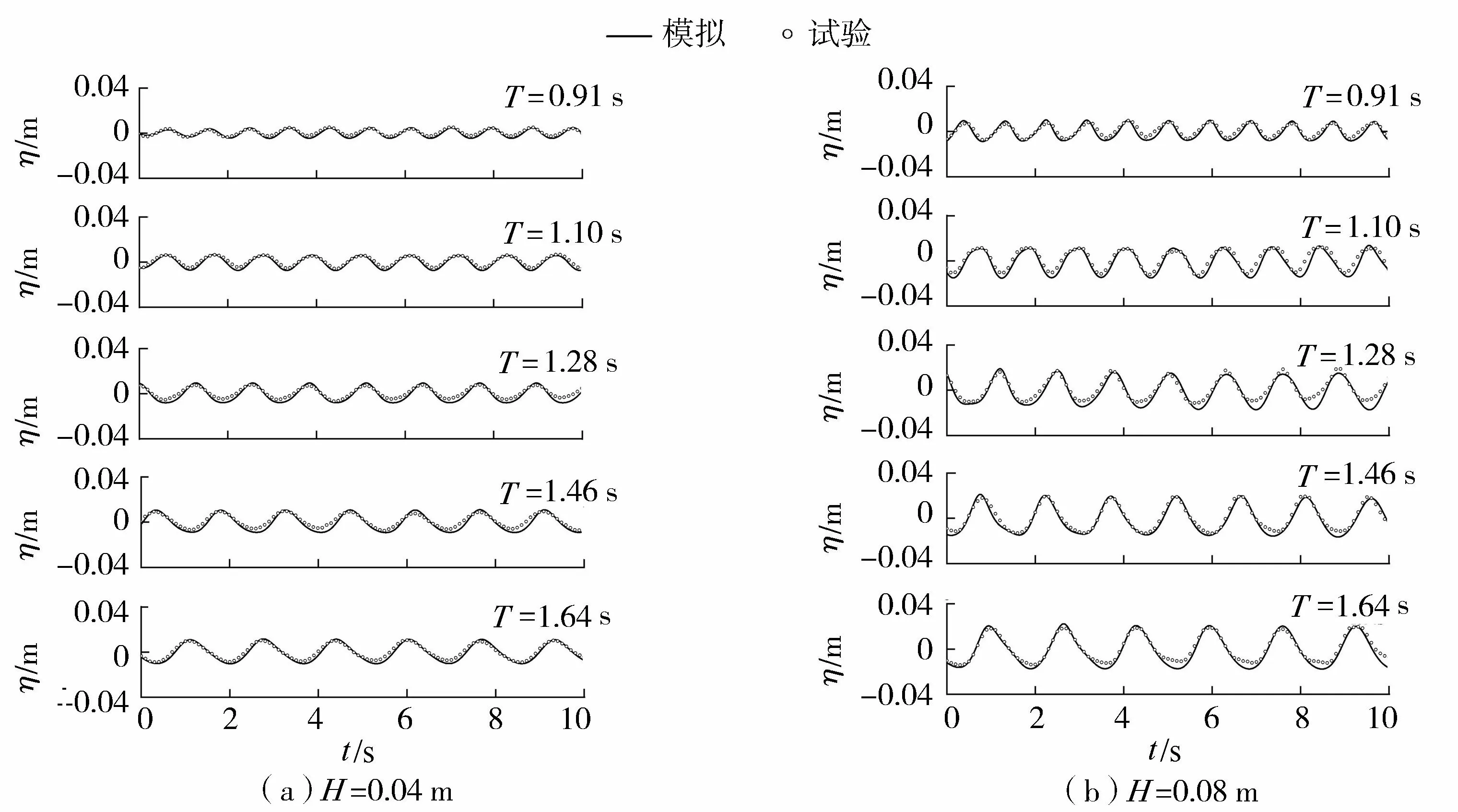
图6 不同周期数值模拟和物理模型试验堤后1.35 m处(G1)波面历时曲线

基于上述数值波浪水槽，图6分别为入射波高H=0.04 m、0.08 m时，不同周期的入射波浪向右传播经过挡板结构物后在G1测点位置处的数值计算和物理模型试验观测的波面η的历时过程。各个波浪周期条件下，G1测点波面历时过程的数值计算结果和试验观测结果吻合良好。数值计算和试验观测结果均表明，随着入射波浪周期的增大，挡板后方G1测点的透射波高逐步增大。这反映出在挡板透空的条件下，入射波浪周期变长，挡板结构后方的掩护效果降低。

2.2.2波压力验证

图7 不同压力测点数值模拟和物理模型试验的压力历时曲线(T=1.10 s)

图7给出了入射波高H=0.04 m、0.08 m且波浪周期T=1.10 s时，挡板迎浪侧的1～5号测点位置处波浪压力历时过程的数值计算结果和试验观测结果的比较。数据结果显示各测点压力的数值计算结果与试验观测结果吻合较好。水面以上的测点压力值均存在数值为0的时间段，这是由于水面以上的压力测点会出现出水而数据回零的情况。

2.2.3底流速验证

图8给出了入射波高H=0.04 m、0.08 m时，不同周期的入射波浪向右传播时挡板底部流速v的数值计算与物理模型试验观测值的比较。各波浪周期条件下，挡板底部流速的数值计算结果与试验观测结果吻合良好。数值计算结果和试验观测数据均表明，入射波高或周期的增加均会增大挡板底部的流速。

上述分析表明，本文建立的数值波浪水槽所模拟得到的波浪与挡板式透空结构相互作用的波面、波压力和底流速历时过程与实测结果均吻合较好。该数学模型可应用于进一步分析波浪作用下挡板式透空结构的水动力学特性。

3 挡板透空结构水动力特性分析

挡板透空结构对波浪的掩护效果主要取决于挡板的入水深度。然而，随着挡板入水深度的增加，结构对波浪的反射作用增强，透射波高降低，但由于在水深方向上，水体在水平方向上的往复运动受到挡板的阻碍作用，挡板两侧水体不可避免的只能通过挡板下方与海床之间的孔隙进行交换，这势必会在很大程度上增加挡板下方的底部流速。为进一步分析挡板透空结构的掩护效果和底部流场特性，基于上述数值波浪水槽，通过改变结构物的相对入水深度(挡板入水深度d/水深h)，对规则波与透空结构相互作用问题展开了数值计算，重点分析挡板的相对入水深度对结构掩护效果和结构下方最大底流速的影响。数值计算的条件和波浪要素与上述物理模型试验中一致，并选取相对入水深度分别为d/h=0.2、0.4和0.8进行水动力特性分析。

图8 不同周期数值模拟和物理模型试验的流速历时曲线

3.1 透射系数

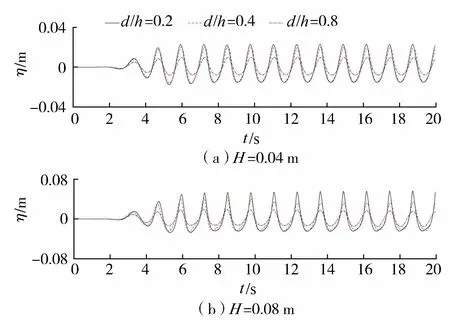
图9 不同相对入水深度时G1处波面历时曲线比较(T=1.28 s)

防波堤的透反射系数是衡量防波堤性能的重要指标之一，而影响其透反射系数的因素很多，如相对水深、相对板宽、相对波长和挡板相对入水深度等，这里主要讨论挡板相对入水深度对透射系数的影响。

图9为在入射波高H=0.04 m、0.08 m和波浪周期T=1.28 s时，不同相对入水深度情况下G1处的波面历时曲线比较。计算结果表明，随着挡板相对入水深度的增加，挡板后方的透射波高逐渐降低，说明增加入水深度可以有效地增强结构的掩护效果。

图10为H=0.04 m、0.08 m时，不同相对入水深度条件下透射系数Ct随波数kh的变化规律，其中k=2π/L。可以看出，当波数一定时，随着挡板相对入水深度的增加，透射系数逐渐减小，说明挡板入水深度增加，结构的掩护效果增强。另一方面，随着波数增加，入射波浪的周期减小，透射系数随之明显降低，这说明对于波长较小或者周期较小的短波情形，挡板式透空防波堤的效果更佳。数值模拟结果显示，当挡板相对入水深度增大到0.8时，对于绝大部分入射波浪情形，透射系数均可降低至0.5以下。

图10 不同相对入水深度的挡板式透空防波堤的透射系数随波数的变化

3.2 底流速

对于工程实际而言，当底流速较大时海床会发生冲刷侵蚀，这将影响海洋生态环境同时也降低结构物的稳定性，因此本节主要讨论挡板透空式防波堤的底部流速问题，包括正向流速和反向流速。

图11为在入射波高H=0.04 m、0.08 m和波浪周期T=1.28 s时，不同相对入水深度情况下，挡板的底流速历时曲线。计算结果表明，不同挡板相对入水深度条件下，挡板底流速变化趋势一致，随着挡板相对入水深度的增加，底流速明显增大。

图11 不同相对入水深度时挡板底流速历时曲线比较(T=1.28 s)

图12为入射波高H=0.04 m、0.08 m时，挡板不同相对入水深度情形下，最大正向和负向无量纲底流速V随着波数的变化关系。底流速的无量纲化是选取正向或负向流速的最大值与波浪传播速度的比值。其中，正向表示流速方向与波浪传播方向一致，负向则表示相反方向。

图12 不同入水深度情况下底部无量纲流速随波数的变化关系

图12中的最大无量纲底流速数据结果显示最大流速的分布在正向和负向上具有一定的不对称性。最大流速的幅值随着波数的增加而减小，这表明对于高频或短周期波浪而言，其传播经过挡板透空结构时，在挡板下方形成的往复流的底流速相对较小。另外，随着挡板相对入水深度的增加，最大底流速的幅值明显增大。特别是在挡板相对入水深度较大时，如d/h=0.8，最大底流速的幅值成倍增加。而且，随着入射波高的增加，底流速也大幅增加。这一点在工程设计上需要特别注意。一般而言，为了谋求更佳的掩护效果，工程人员通常需要增大挡板的入水深度，以达到有效降低透射波高的目的。但同时会使得底部流速大幅增加，这将会对海床形成局部冲刷，进而对结构的安全形成威胁。实际应用时，工程设计人员需结合底流速的具体情况，增设人工护底，以保证海床的稳定性。

4 结 语

本文应用开源计算流体力学软件OpenFOAM，基于有限体积法建立了波浪与挡板透空结构相互作用的二维数值波浪水槽，并通过规则波与挡板透空式防波堤相互作用的物理模型试验进行了验证，结果显示波面、压力和流速的数据结果吻合良好。数值计算结果表明，增加挡板的相对入水深度可有效降低波浪的透射系数。当相对入水深度为0.8时，挡板透空结构对波浪的透射系数可降低至0.5以下。另外，随着挡板相对入水深度的增加，底部水体往复流动的速度也明显增大，这需要引起工程技术人员的额外关注。