基于格子玻尔兹曼方法的液滴撞击移动液膜过程模拟

袁 浩，黄宏宝，郭平措，何小泷

(1.重庆交通大学重庆西南水运工程科学研究所，重庆 400074；2.四川大学水力学及山区河流开发保护国家重点实验室，四川 成都 610065；3.青海省水利水电勘测设计研究院，青海 西宁 810001)

液滴撞击液膜现象广泛存在于泄洪雾化、喷墨打印、雨滴冲击地面积水等自然和工程现象中。通常液滴撞击固壁边界后在固壁上发生聚集现象形成液膜，随后发生液滴撞击液膜现象。早期研究表明液滴撞击液膜后演化过程主要与液滴碰撞速度、流体性质、液膜厚度及壁面物理化学性质相关。

迄今为止，前人对液滴撞击液膜过程进行了大量试验及数值模拟研究。试验研究主要通过高速摄像机捕捉液冠演化过程，并分析各无量纲参数对液冠演化过程的影响，主要包括雷诺数Re、韦伯数We和液膜厚度[1-3]。Rioboo等[3]通过试验研究将液滴撞击液膜后形态演化分成了融合、反弹、部分反弹、液冠及飞溅5种情况。试验结果表明液冠半径与无量纲时间的平方根成正比[1-2]，液滴撞击液膜后在液膜中形成的速度不连续性是液冠形成的原因[1]。然而液膜并非静止的，通常会在平面上发生流动。Alghoul等[4]首先研究了液滴撞击移动液膜的过程，随后不同参数对液滴撞击液膜的影响研究相继展开，如Castrejón-Pita等[5]将液滴撞击移动液膜的形态归纳为融合、剧烈飞溅、部分或完全反弹以及液冠这4种形态，而形态演化的主要影响参数是初始液膜运动速度和碰撞速度；Gao等[6]研究了液冠延伸率和液冠半径随时间的变化，通过试验研究得到了液滴撞击移动液膜时液冠半径与时间的关系和液冠纵向延伸率变化规律。

宏观数值模拟可以获得液冠演化及破碎过程中流场及涡量场的详细变化过程，主要包括边界积分法和基于N-S方程与界面追踪方法的多相流模拟方法。研究者们利用此类方法分析了液滴飞溅的临界条件，指出液冠半径与无量纲液冠演化时间成正比，其破碎的原因是液冠末端的Rayleigh-Taylor不稳定性[7-10]。格子玻尔兹曼方法(lattice Boltzmann method，LBM)作为一种宏观数值模拟方法，已经发展成为研究复杂多相流现象的有效数值模拟方法，被用于多种液滴撞击液膜的复杂多相流现象的模拟。与传统宏观多相流数值模拟方法相比，LBM优势[11-13]在于：①可以实现完全并行和分块计算；②避免了传统宏观方程中的非线性对流项的处理，只需要求解一系列线性方程组；③压力仅与流体状态方程相关，不需要求解泊松方程来获得压力。其中LBM伪势模型由于其简洁性和计算便利性被广泛应用，该模型不需要进行界面跟踪，通过粒子间作用的伪势可以自动形成两相交界面[14]，已被成功用于液滴撞击静止液膜的研究[15-17]。目前基于液膜静止过程的研究还缺乏对液冠演化过程的精确验证，无法保证模型模拟的准确性[15-20]。由于液滴撞击液膜过程中液膜往往无法保持静止，因此研究液滴撞击移动液膜的过程具有非常重要的意义。

本文通过LBM伪势模型模拟了液气密度比为720条件下液滴撞击移动液膜的过程，分析了液膜运动速度等参数对液冠形态演化的影响，并将结果与现有半经验公式进行对比，以分析液冠半径及液冠高度随时间的变化规律，可为深入揭示复杂条件下液滴撞击液膜过程相应机理提供参考。

1 数值模型

本文主要采用多松驰时间(MRT)碰撞算子实现流体对流过程模拟，以获得更好的数值稳定性。采用MRT碰撞算子的相应粒子分布方程[21]可以表示为

(1)

(2)

宏观密度ρ和流场实际速度u可通过以下公式[11]求得

(3)

本文采用的外力格式为Li等[21]提出的满足热力学一致性的外力格式

Fx,-Fx,Fy,-Fy,2(uxFx-uyFy),uxFx+uyFy)T

(4)

式中：ε为调节热力学一致性的参数；ψ为粒子间的伪势；Fx、Fy、ux、uy分别为作用在粒子上的合力F和流场实际速度u在x、y方向上的分量；Fm为粒子间的相互作用力。本文计算伪势ψ时引入Carnahan-Starling(C-S)状态方程[22]：

(5)

式中：a、b、R为相关参数，取值为a=0.25，b=4，R=1；Tc为临界温度；Pc为临界压力。

为获得可单独调节表面张力的模型，式(1)中源项C[21]为

(6)

式中Q可以通过下式求解[21]：

(7)

式中：κ为表面张力调节参数；G为粒子之间的相互作用强度；ωi为不同离散速度方向的权重系数。

2 模型验证

2.1 边界及初始条件

液滴撞击移动液膜计算示意图及液冠形状演化相关参数如图1所示，计算区域为1 001×301矩形区域，图中r0为液滴初始半径，H为液膜厚度，u0为液滴撞击液膜的速度，uf为初始液膜运动速度。计算域上部边界及左右边界为非平衡外推边界，底部边界为无滑移边界。结合液相密度ρl、液相黏滞系数υl、表面张力σ和时间t可以获得液滴撞击液膜时液冠演化形态的控制性无量纲参数：

(8)

式中：Re为雷诺数；We为韦伯数;h*为液膜无量纲厚度;t*为无量纲时间;u*为初始无量纲液膜运动速度。液冠形状演化过程中相应参数如图2所示，图中rc为液冠半径，Hu为液冠上游高度，Hd为液冠下游高度，对3个参数进行无量纲化：

(9)

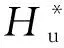
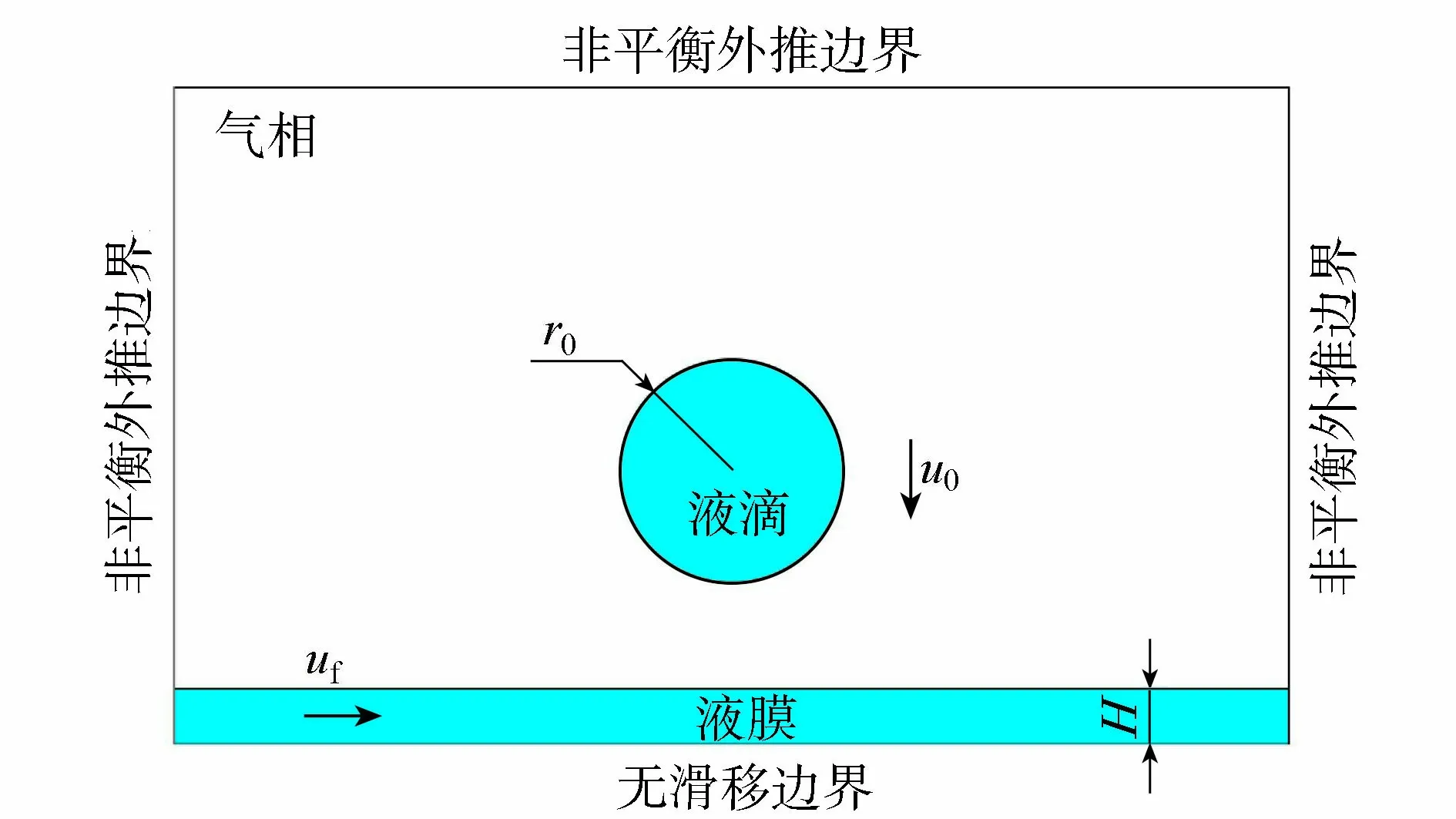
图1 液滴撞击液膜计算区域示意图

图2 液冠演化过程示意图

液滴周边和液膜附近密度场分别通过式(10)(11)初始化：

(10)

(11)

式中：(x0,y0)为液滴中心；ρg为初始汽相密度；y1为气液交界面位置；w为初始界面宽度，考虑到计算稳定性和物理真实性，设为5。

2.2 液滴撞击静止液膜验证

首先利用液滴撞击静止液膜的演化过程来验证模型的可靠性。液滴初始半径r0=50，液膜厚度H=25。本文采用等温模型，选取初始温度T=0.5Tc，对应液气密度比ρl/ρg=720。液滴撞击液膜速度设置为u0=0.125，初始无量纲液膜运动速度u*=0，松弛系数τυ=0.537 5，表面张力调节参数κ=0.2，对应表面张力σ=0.008 3。相应的Re和We分别为500和87.8。液滴撞击液膜后液冠形态演化过程如图3所示。

图3 液滴撞击静止液膜不同时刻液冠形态演化过程

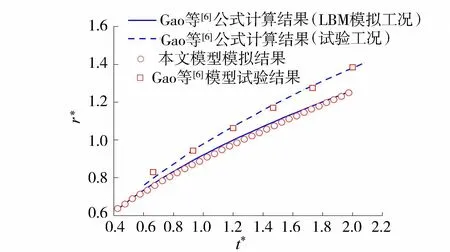
图4 液滴半径演化过程验证

图5 液冠垂向延伸率演化过程验证

液滴半径演化过程本文模型模拟结果与Gao等[6]半经验公式计算结果对比如图4所示，可见两者结果一致。对比发现Gao等[6]模型试验结果在演化过程中，其半径变化略小于公式计算值，其原因在于Gao等[6]在公式推导过程中假设在液冠形成之前液滴会与液膜完全融合，这一假设与试验现象[3]和数值模拟结果[10,14,18-20]存在差异。进一步将本文模型模拟结果中的液冠垂向延伸率St与Gao等[6]半经验公式计算结果进行对比，结果如图5所示。在t*=0.500～1.200时，本文模型模拟结果与Gao等[6]半经验公式计算结果吻合良好，但当t*=1.200～1.500时，本文模型模拟结果突然增大，此时发生液冠不稳定现象，液滴开始脱落，导致液冠垂向延伸率增大。随着液滴脱落，在t*=1.500～2.000时，液冠垂向延伸率迅速下降，低于Gao等[6]半经验公式计算结果。

3 模拟结果与分析

为分析不同Re、We和u*对液冠演化的影响，选取的相关参数如表1所示。模拟过程中保持液滴撞击速度不变，通过调节τυ和κ获得Re和We。

表1 液滴撞击移动液膜相关参数

3.1 Re的影响

不同Re条件下液滴撞击液膜过程如图6所示。随着Re的增大，上、下游液冠厚度减小，同时液冠高度增大，液冠更容易发生破碎。受到初始无量纲液膜运动速度u*的影响，上、下游液冠演化过程呈现不对称性。当t*=1.250时，在Re=500和Re=1 000条件下上游液冠均已发生破碎；当t*=2.000时，在Re=1 000条件下上游液冠已发生二次破碎，但在Re=200条件下上游液冠此时才发生破碎。不同Re条件下，整个演化过程中下游液冠并不发生破碎。

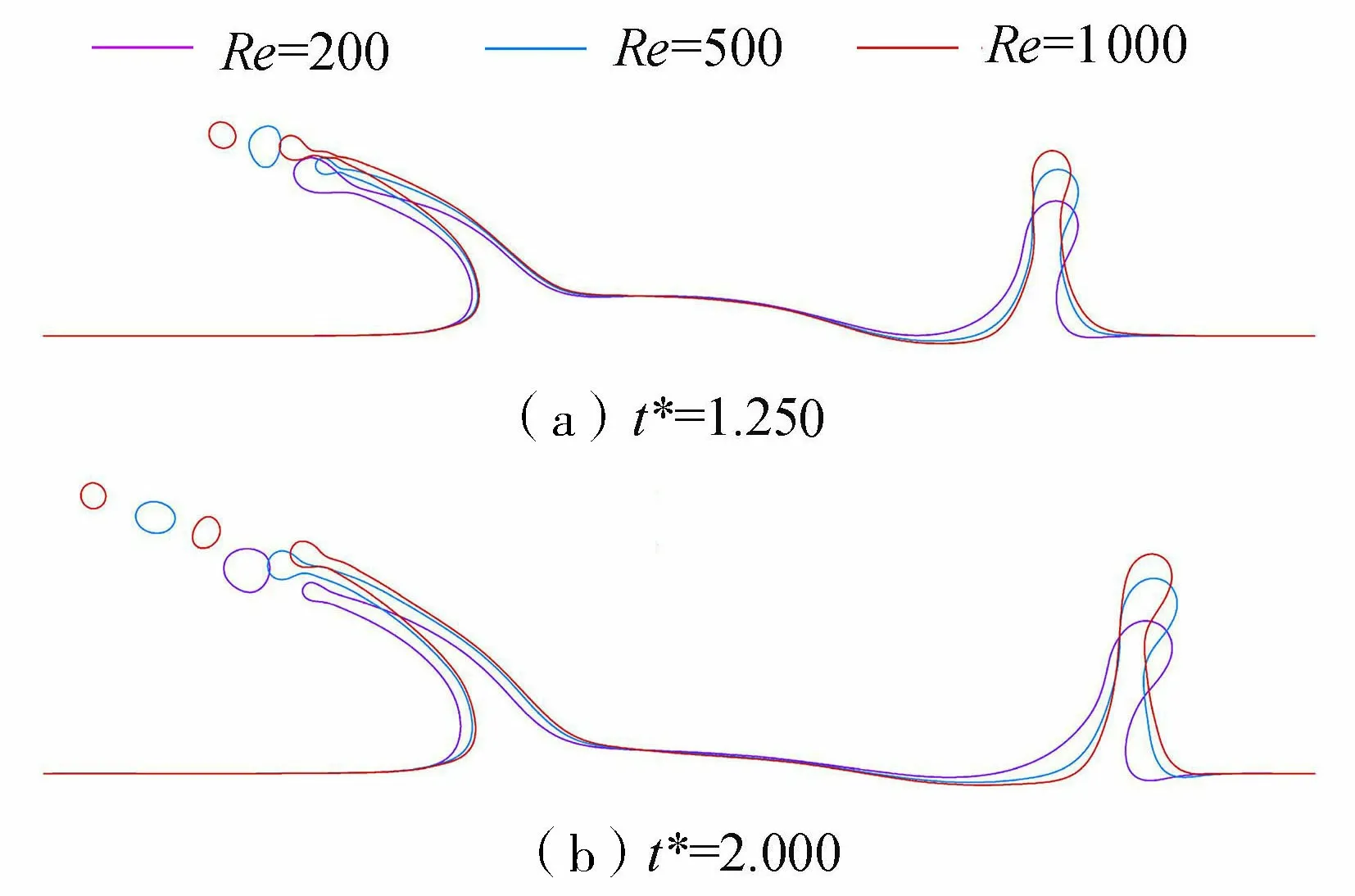
图6 不同Re条件下液滴撞击移动液膜时液冠演化形态

图7 不同Re条件下液滴撞击移动液膜时液冠参数演化过程

不同Re条件下，上、下游液冠高度和半径演化过程如图7所示。上、下游液冠高度均随Re的增大而增大，且在同一时刻上游液冠高度大于下游液冠高度。此时液滴撞击液膜后产生的环向速度与初始液膜运动速度相反，上游液冠处撞击后液膜运动速度不连续性增大，促进了上游液冠生长和破碎过程。而下游液冠处撞击后产生的环向速度与初始液膜运动速度方向相同，减小了下游液冠处撞击后液膜运动速度不连续性，抑制了下游液冠的生长。根据Gao等[6]的半经验公式，在Re=200、500、1 000条件下对应的能量损失系数分别为0.50、0.52和0.52，本文模型计算结果与Gao等[6]的半经验公式计算结果十分吻合(图7(c))。

3.2 We的影响

不同We条件下液滴撞击液膜过程如图8所示。上游液冠随We的增大末端Rayleigh-Taylor不稳定性增强，表面张力减小后液冠难以维持稳定形态更易发生破碎。破碎液滴大小也随We的增大而减小，在t*=1.250时，不同We条件下液冠均可以观察到明显的二次破碎。下游液冠稳定性也随着We的增大而减小，但均未发生破碎。当We=1 165.5时下游液冠变形远大于We=87.8、139.4时下游液冠变形。

图8 不同We条件下液滴撞击移动液膜时液冠演化形态

不同We条件下，上、下游液冠高度和液冠半径演化过程如图9所示。上游液冠高度不随着We的增大而增大，而下游液冠高度随着We的增大而增大。在同一时刻下游液冠高度大于上游液冠高度。上游液冠受到初始液膜运动速度的影响，Rayleigh-Taylor不稳定性增强，末端极易发生破碎，导致上游液冠高度接近。但初始液膜运动速度抑制了下游液冠的Rayleigh-Taylor不稳定性，致使下游液冠并不易发生液滴脱落。同时表面张力随着We的增大而减小，液冠抗变形能力降低，大We时下游液冠变形更大，因此液冠高度更高。由图9(c)可知，We的变化也不影响液冠半径的演化。当We=87.8、139.4、1 165.6时对应的能量损失系数分别为0.52、0.51和0.49，We对液滴撞击液膜过程中能量损失系数变化的影响可以忽略，本文模型计算结果与Gao等[6]的半经验公式计算结果十分吻合。

图9 不同We条件下液滴撞击移动液膜时液冠参数演化过程

3.3 初始无量纲液膜运动速度的影响

不同初始无量纲液膜运动速度条件下液滴撞击液膜过程如图10所示。上、下游液冠高度均随初始无量纲液膜运动速度u*的增大而减小。当t*=2.000时，在u*=0.8和u*=1.0条件下液冠末端均出现二次破碎。随着u*增大，上游液冠处液滴撞击产生的环向速度与初始液膜运动速度方向相反，上游液冠处撞击后液膜运动速度不连续性增大，导致上游液冠末端Rayleigh-Taylor不稳定性增强。而下游液冠处液滴撞击产生的环向速度与初始液膜运动速度方向相同，下游液冠处撞击后液膜运动速度不连续性减小，下游液冠Rayleigh-Taylor不稳定性随之减小。

图10 不同初始无量纲液膜运动速度条件下液滴撞击移动液膜时液冠演化形态

不同初始无量纲液膜运动速度条件下上、下游液冠高度和液冠半径演化过程如图11所示。上、下游液冠高度均随着初始无量纲液膜运动速度u*的增大而减小，上游液冠飞溅角受到初始液膜运动速度和液滴撞击速度的共同作用，随着u*增大，上游液冠飞溅角减小。液冠半径随u*增大而增大，当u*=0.5、0.8、1.0时对应的能量损失系数分别为0.52、0.58和0.62，随着u*增大，撞击过程中能量损失系数增大，由图11(c)可知，本文模型计算结果与Gao等[6]的半经验公式计算结果十分吻合。

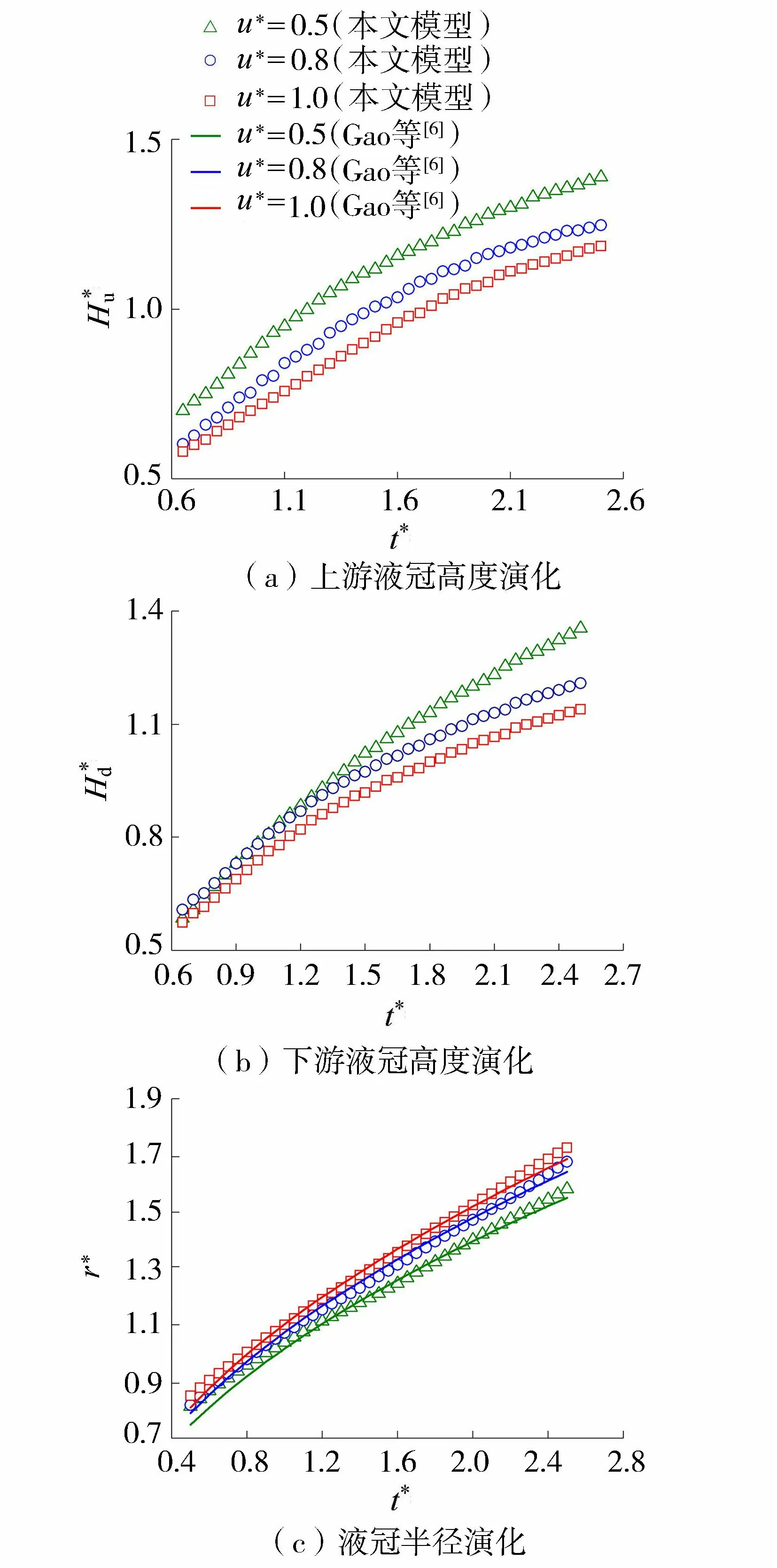
图11 不同初始无量纲液膜运动速度条件下液滴撞击移动液膜时液冠参数演化过程

4 结 论

a. 受到初始液膜运动速度的影响，上游液冠处撞击后液膜运动速度不连续性增大， Rayleigh-Taylor不稳定性加剧，更易发生破碎。而下游液冠处撞击后液膜运动速度不连续性减小，下游液冠更稳定。

b. 上、下游液冠高度均随Re的增大而增大，但液冠半径演化过程不随Re的增大而改变。

c.We的变化影响到液冠末端稳定性，上游液冠高度不随We增大而改变，下游液冠随We增大而发生剧烈变形，液冠高度随We增大而增大。

d. 随着初始无量纲液膜运动速度u*的增大，液滴撞击过程中能量损失系数增大，上、下游液冠高度均减小，液冠半径则随u*的增大而增大。