基于几何光学近似迭代的多重散射波面分析
彭梓齐,杨江河
(湖南文理学院数理学院,中国 常德 415000)
光学遥感作为成熟的测量技术在工业、医疗、环保等领域得到了广泛应用[1-7]。在光学遥感应用中,光在媒质中的传播效率是影响光学测量结果与精度的一项重要参数。在散射粒子大量存在的高散射媒质(生物组织、大气云层等)中,可视光以及红外波段光会发生强烈的散射现象[8-12]。多重散射不仅使光波能量发散,导致传播效率低下,同时使散射光偏光面发生变化,降低光学相干性,导致入射光原有的光学特性发生变化。如果能在高散射媒质中建立一种高效、稳定的传播方法,将有利于提高光学遥感的测量范围与精度。
环形波面的调制光在空气中长距离传播时,通过自身干涉效果可以形成一类强度分布为近似贝塞尔函数的波面。具有类波面的光通常被称为非衍射光。理想的非衍射光波面中心集中大部分能量,波面强度分布不随传播距离的变化而变化,整个波面有抑制衍射的效果[13-17]。相比高斯分布的光源,在远距离传播的情况下环状光在中心部位有着极高的传播效率。
在前期的研究中[18-20],我们研究了在散射媒质中环状光的传播特性。通过实验发现:收紧光学接收机视野角(3 mrad)的前提下,在特定浓度与深度的高散射媒质中,环状光经过4~5次的多重散射之后,最终在出射面中心部形成中心波峰强度相对较高的干涉光,且中心主瓣周围存在强度较弱的旁瓣。针对这一现象,还需要进一步的理论分析与数值解析。
数值解析不仅可以帮助验证前期实验结果的真伪,还为后期实验的可行性提供分析与参考,是一项十分重要的内容。米氏散射理论是众多散射理论中最为常用的理论之一,它以球体为散射解析对象,通过把电磁波的边界条件代入球体模型,然后对电磁波传播过程进行严密的求解从而得到球体后方的散射强度分布。这样求得的单个球体散射模型被称之为单散射。在针对多个散射球体同时存在且个数较少的情况下可以利用巴比涅原理对单散射模型进行叠加来实现分析多个球体的散射。另外,求解格林函数并进行叠加也是常见解析方法之一[21-23]。
前期研究的结果采用的散射媒质浓度较高,媒质中散射粒子极多,且粒子间距极小,这样导致了粒子间发生多重散射,且粒子产生的散射光之间可能存在干涉效果,在这种情况下,采用米氏散射模型的叠加算法不能体现多重散射以及微小距离间散射光相互干涉的效果。在前期研究的实验条件中,我们引入了收紧接收机视野角测量前方散射光的测量方法,在解析中同样需要针对前方散射光的分析方法。根据以上条件,本文提出了一种基于简化几何光学近似的迭代解析方法,分析了环状光多重散射现象中的前方散射光强度。在本文中,笔者首先叙述了简化几何光学近似的原理,运用该原理对单散射模型进行计算并与米氏散射理论结果比较,验证了简化几何光学近似法的计算精度。在此基础上,利用蒙特卡洛模拟与迭代方法,提出了一种由单散射过程迭代来实现多重散射的效果计算方法,对环状光在散射媒质中的传播进行了分析,并与实验结果进行比对,评价了该分析方法的可靠性。
1 解析算法
前期研究采用了一般市场贩卖的低脂肪加工纯牛奶的稀释液作为的高散射媒质的模型。加工纯牛奶中脂肪球粒子大小相对均一,粒子浓度调节相对准确,适合作为散射媒质模型。采用的加工纯牛奶中所含散射粒子主要为脂肪球的脂类与酪蛋白的蛋白质,平均粒子直径分别为1.1 μm与0.1 μm。与脂肪球相比,酪蛋白粒子直径只有脂肪球的1/10左右,散射截面大小只有脂肪球的1/100左右。酪蛋白粒子散射强度相比脂肪球粒子散射强度十分微小。实验中采用了波长为660 nm的半导体激光作为光源,相对于波长为660 nm的光源,脂肪球粒子发生米氏散射,其异向性参数g的大小为0.936,散射光几乎都集中在入射光轴方向。另一方面,酪蛋白粒子直径远小于光源波长,散射类型为瑞利散射,散射光在每个方向上的分布几乎是均等的。根据这两个条件,在收紧接收器视野角,观测前方散射光的实验前提条件下,解析中可以忽略酪蛋白产生前方散射光。本研究的解析算法中只考虑了脂肪球的散射影响。
1.1 粒子单散射模型
在粒子直径大于光源波长的情况下,通常采用米氏散射理论[24]来分析球形粒子的单散射模型。米氏散射的散射强度受光源的波长影响小,而主要受散射角的影响。随着粒子直径的增大,米氏散射中的前方散射光部分也会逐渐增强。研究表明,散射粒子直径相对较大的条件下,运用几何光学近似法分析的单散射模型与米氏散射的分析结果基本一致[25,26]。此外,几何光学近似采用菲涅尔解析可以准确计算出近场空间的散射光。基于以上理由,本文采用了几何光学近似作为解析工具。
一般的几何光学近似手法会考虑在散射球体上所发生的反射、折射、衍射过程,综合分析散射强度[24]。由于前期研究实验中测量的是前方散射光,本文采用的几何光学近似也只考虑透射与衍射,而忽略了在前方散射上效果微弱的反射。光在穿过球体界面时,发生较大偏转的折射光几乎不能被小角度接收机接收,本次解析中为了简化计算,我们同时忽略了光线在散射球体内部的折射偏转,当光线穿过散射球体时,以直线光程来考虑。简化后的几何光学近似的模型如图1所示。在多重散射光的干涉效果定量分析上,一般需要考虑到由多重散射所引起的偏光面变化,而前期研究中测量的前方散射光其偏光面基本不发生变化[20],所以在本解析方法中忽略了偏光面变化,直接采用了菲涅尔衍射公式来计算单散射的散射强度,散射光振幅大小可用下式来计算:
(1)
式中,u,u0分别为入射面与观察面上入射光与散射光的振幅;(x0,y0)和(x,y)分别为入射面与观察面上的位置坐标;k为波数;l为(x0,y0)到(x,y)上的距离,dσ为积分微小光源的宽度。对于任意观察点,参照图1,其光程l可用下式表示:
目前她已成为采油厂唯一的女油藏专家。工作十余年来,先后有150余项科研成果获厂级以上奖励,参与“孤岛中一区Ng3聚驱后井网调整非均相复合驱”等9项中石化、油田分公司重大先导试验项目,创直接经济效益3亿余元。
l=l1·n1+l2·(n2-n1),
(2)
式中,l1为几何光程;l2为光线穿过散射球体内部时球体内部的光程差;n1,n2分别为媒质折射率与散射球体折射率。
在光程l的计算中,由于媒质内部的散射球体的分布是随机的,需要确认二次波光线传播方向与散射球体位置的相互关系。一般的方法是用随机数确定粒子位置,然后从粒子位置与光线方向之间的关系来计算光程长度[27,28]。为了缩短计算时间,本研究采用新的算法来计算光程,平面的计算原理图如图2所示。

图1 几何光学近似Fig. 1 Geometric optics approximation
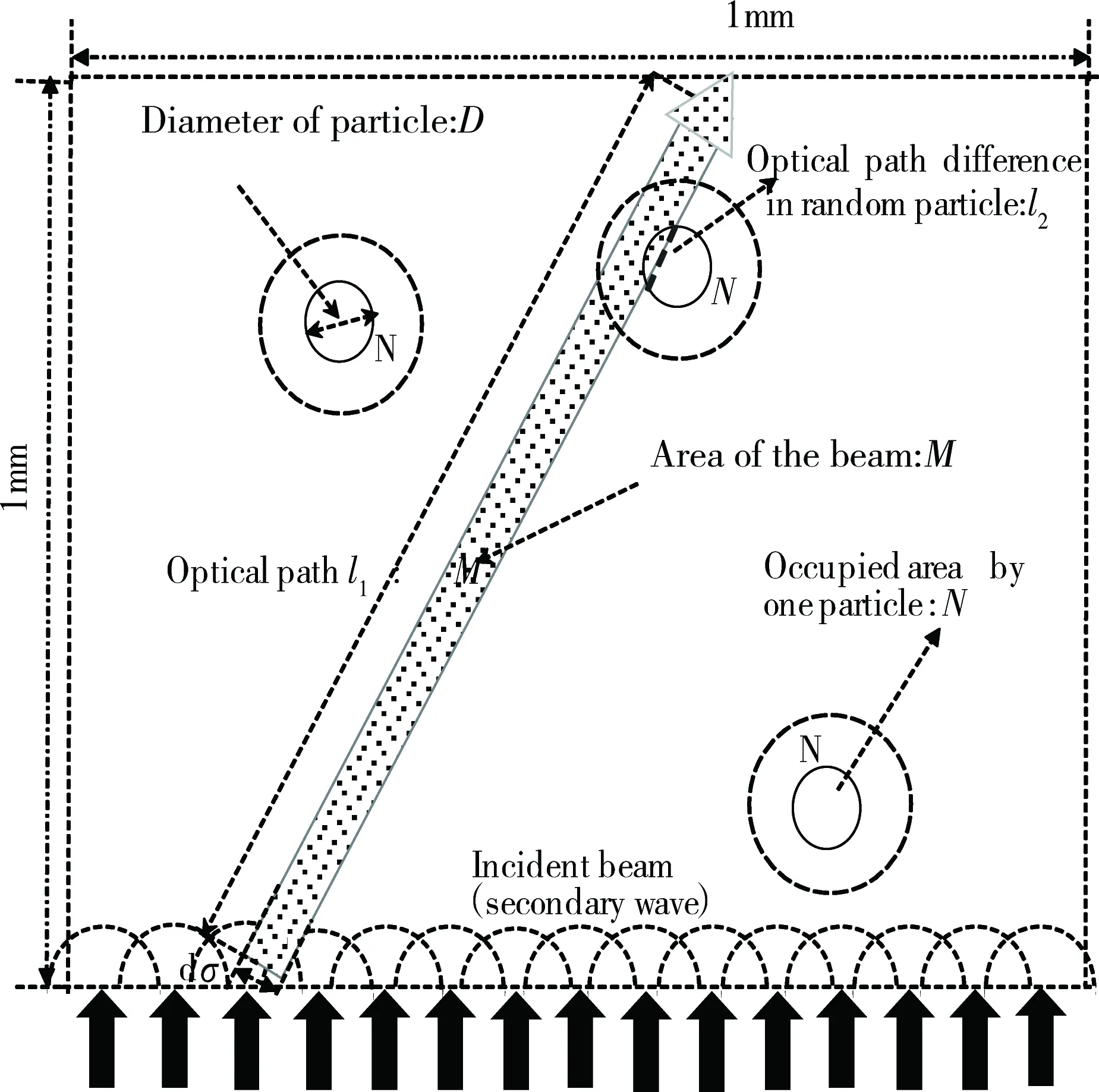
图2 散射媒质中的光程计算图示Fig. 2 Optical path calculation when light transmits in random media
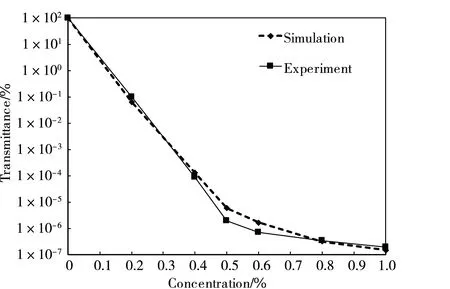
在1 mm长度的立方体空间内,式(1)中宽度为dσ的微小光源(对应图1中的一条光线)在穿过该空间时,在平面上投影面积为M=l1* dσ。根据散射媒质的浓度以及图2平面模型的物理厚度可以算出在1 mm×1 mm的平面内存在n’个散射球体。假设这些散射球体在平面上的投影不重叠且均匀分布,那么每个粒子在1 mm×1 mm的平面上所占有的面积为N= 1/n’ (mm2),每个散射球体在自己占据的面积内随机运动。在这种情况下,把微小光源的光线与散射球体发生碰撞冲突的概率简单的定义为S=M/N。通过产生0~1区间的随机数R,在R>S的情况下光线不穿过散射球体,散射球体内部光程长l2为0;当R 前期研究中所用散射媒质为脂肪浓度1.8%的加工牛奶的稀释液。稀释浓度以0.1%为单位,最高浓度为1.0%(本文中所述“牛奶浓度”均指稀释浓度,牛奶浓度1.0%指将加工牛奶稀释100倍后的溶液)。媒质容器为长度20 cm的立方体玻璃水槽。实验结果表明,在牛奶浓度为0.8%~1.0%的浓度范围内,可以明显观测到中心干涉光效果[18-20]。根据浓度以及脂肪球的其他参数,使用下式可以求出光在此散射媒质中的平均自由程。 (3) 式中,a为脂肪球半径;n为单位体积中的散射球体个数,Q为散射截面参数的Q值,g为异向性参数。 图3 多重散射的分析模型(上方视角) Fig. 3 Analysis model for multiple scattering (view from above) 假设所有脂肪球在入射光方向上的投影没有重叠,参考脂肪球的直径大小、折射率以及生成中心干涉光时的牛奶浓度,可以计算出产生中心干涉光时光在散射媒质中的平均自由程为4~5 cm。实验中采用的媒质容器长度为20 cm,可以计算出从环状光入射散射媒质到射出散射媒质的过程中会发生4~5次散射,所以计算观察面的波面时应考虑多重散射的效果。 为了将1.1节中所述简化几何光学近似的单散射模型扩展利用到多重散射模型中,我们将整个散射媒质在空间上分割成若干层,同时将每层分割为若干更小的单位空间。在每个单位空间中存在的散射球体数极少的情况下,可使用简化几何光学近似作为单散射模型处理。具体的媒质分割处理的平面图如图3所示。 为了检验1.1节中所提出的简化几何光学近似在单散射计算上的准确性,我们计算了空气中水球体的散射光强分布,同时与米氏散射理论的计算结果进行了比较。计算中光源波长为630 nm;散射球体相对折射率为1.33;散射球体直径分别为4,10和15 μm。 计算结果如图4所示,横轴为散射角度,纵轴为散射强度。由于几何光学近似的计算手法中存在米氏散射计算中未考虑的直射光,几何光学近似的计算结果在0°到1°的区间包含了极强的直射光强度,因而去掉了0 °到1 °附近的计算结果便于比较。从比较结果来看,在1°到15°附近的范围里,散射强度的峰值以及该峰值所出现的散射角基本一致。在评价光轴附近的前方散射光的计算中是有效的。由于直射光的原因,两者在0°到1°区间上有明显的数值区别,在实验中接收机所测量前方散射光中也包含了直射光的成分,实际的多重散射解析计算中,与实验一样直射光成分并未被去除,而是包含在计算中并在迭代计算中体现。 图4 单散射波形计算结果 (a) 几何光学近似. (b) 米氏理论Fig. 4 Single scattering waveform calculated by (a)Geometric optics approximation. (b) Mie theory 运用1.2节中所示的分割迭代计算的解析方法,计算散射媒质中光的透射率以及环状光传播的散射波面。计算中光源波长为660 nm,脂肪球平均直径设为1.1 μm,水与脂肪球的折射率分别为1.33与1.45。 图5 高斯光在散射媒质中的透射率 Fig. 5 Transmittance of Gaussian beam in random media 在光的透射率计算中,入射光为宽度6 mm的高斯光,通过在200 mm长的牛奶稀释液中的传播后,计算等宽部位入射前后的光强,将其比值作为透射率。计算所得透射率与实验所得透射率如图5所示。可以看出随浓度变化的透射率在计算结果与实验结果上是一致的,验证了2.1节中所述直射光部分的正确性。散射媒质在0.1%~0.4%的范围内,主要受单散射支配,透射率随着浓度的升高而急剧下降。通过朗伯-比尔定律可知,媒质的散射系数σ可以由透射率的对数对浓度求微分而得到[29]。在浓度0.1%~0.4%范围内,可依据图5中透射率曲线的斜率求得散射系数σ1为158 cm-1,结果与通过米氏散射理论所计算的散射系数一致。在散射媒质浓度为0.5 %以上的区域,多重散射的效果逐渐增大,随着浓度的增加,透射率的衰减率逐渐减小。当散射媒质浓度超过0.8%时,多重散射逐渐占据主导地位,通过图5的透射率曲线斜率可以求得此时的散射系数为23 cm-1。把前方散射光作为透射光的一部分情况下,考虑到异向性参数g为0.936,在浓度为0.8 %的情况下,根据米氏散射理论所计算出的散射系数为23.3 cm-1。这与前述的透射率斜率计算结果也是一致的。其中异向性参数g的计算式如下式所示。 (4) 式中,θ为散射角;p(θ)为散射角为θ时的概率函数。 运用相同的计算方法,我们计算了与实验参数相同的环状光散射光波面,散射媒质长度为200 mm。环状光参数设定为直径40 mm,环厚3 mm。图6(a)和(b)分别为牛奶浓度0.8%和1.0%时散射光波面的解析结果与实验结果。牛奶浓度0.8%时,计算结果在波面中心出现了干涉波峰,其宽度与实验结果相同。牛奶浓度1.0%时,计算结果在波面中心、左右两侧处出现了多个波峰,而实验结果在波面中心、左右8 mm处出现了3个波峰。从比较的结果来看,本文采用的基于简化几何光学近似的迭代方法在多重散射的计算中是一种有效的模型。 我们也计算了牛奶浓度0.9 %时环状光入射散射媒质所产生的散射波面。图7(a)为牛奶浓度0.8%~1.0%时散射波面变化的计算结果,随着散射媒质浓度的降低,散射光波面光强逐渐增强,散射波面中心干涉波峰强度也逐渐增强,而周围的旁瓣有向中心靠拢的趋势。另一方面,在对牛奶浓度0.8%的散射媒质分别静置11,49和86 min后,我们将直径40 mm,环厚1 mm的环状光入射到散射媒质中,实验结果如图7(b)所示。随着静置时间的增长,散射媒质中的散射粒子逐渐沉淀,媒质容器中心部位的粒子浓度逐渐下降,散射波面的强度逐渐上升,中心的干涉波峰的大小也逐渐增大,旁瓣有逐渐向中心靠拢的趋势。该实验结果与计算解析结果呈现了相同的趋势。虽然干涉波峰、旁瓣在位置、宽度上的一定的差异性,这是由于图7(b)的实验采用了不同参数的环状光(环厚1 mm),同时该实验结果出现时的浓度与计算结果上存在差异。通过计算可以知道,对于同样大小的环状光,在环厚比较细的情况下,更容易在近距离上相互干涉产生非衍射光[18]。相比于图7(a)的计算结果,在图7(b)的实验中由于采用环厚更细的环状光,在低于0.8 %浓度的散射介质中产生了中心干涉光,这符合理论依据。 图6 环状光在各浓度的散射媒质中的散射波形 (a)0.8%, (b)1.0%Fig. 6 Annular beam propagation pattern in random media at concentration of (a)0.8%, (b)1.0% 图7 环状光在各浓度散射媒质中波形的变化 (a)仿真结果;(b)实验结果Fig. 7 Variation of annular beam propagation pattern in random media with different concentration (a) Simulation; (b) Experiment 然而在图6中,依然可以看到理论计算与实验结果在散射波形的旁瓣上存在的微小差别。这是因为受到多重散射的影响,波面在时间与空间上都会产生一定的波动,导致散射光在到达测量平面时相干性降低。而在本文中所讨论的手法中我们假设了所有的光子都具有相干性、并没有考虑到散射媒质的波动对散射光相干性的影响。所以在图6(b)中,对相干性要求相对严格的旁瓣位置上,由于多重散射对相干性的影响,实验结果的旁瓣波峰并不明显。 本研究以几何光学近似为基础,运用迭代算法对环状光在散射媒质中的传播进行了数值分析。在单散射模型中,我们运用了简化的几何光学近似进行计算,其结果与米氏理论的散射结果一致,证明了该简化几何光学近似在散射计算中的可靠性。在此基础上,运用迭代算法实现了多重散射的模型。通过透射率的计算,我们发现中心干涉光在散射媒质中出现时,散射媒质的浓度介于发生单一散射与多重散射的浓度之间。在环状光散射波形的分析中,计算的散射波形的中心干涉波峰与旁瓣的振幅、位置与实验结果一致。同时观察到随着沉淀过程的进行,散射波形变化的该过程与计算结果显示了同样的趋势。随着浓度的升高,中心干涉光波峰逐渐强度逐渐提高,旁瓣逐渐向中心位置移动。 在实际的应用中,若要利用环状光在散射媒质中的该传播特性,不仅需要调整散射媒质的浓度,其他光学参数(传播距离、散射粒子的种类、大小、折射率、光源的调制形状等)也需要相应的调整与控制。本文提出的基于几何光学近似的迭代算法可以调整、控制相应参数,可在数值计算上优化环状光在散射媒质中传播效率,为实验提供有效的理论依据。 若需完全构建与实验条件相同的散射模型,在后续工作中需要在数值计算中加入散射媒质实时波动对干涉性的影响。同时运用该算法,探索在更高浓度的散射媒质中形成中心干涉光的条件。1.2 多重散射模型
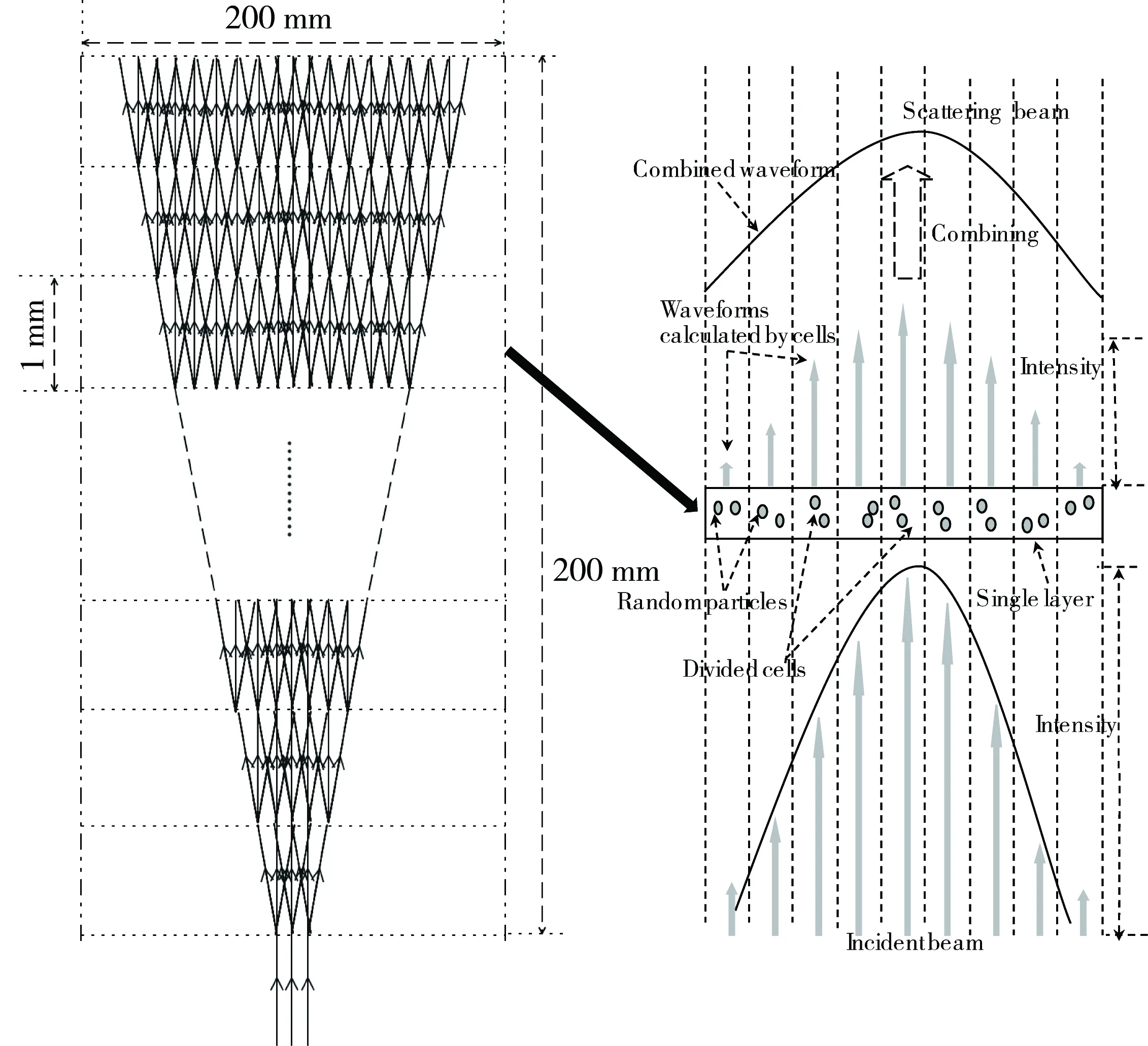
2 解析结果
2.1 单散射模型计算结果评价

2.2 多重散射解析结果
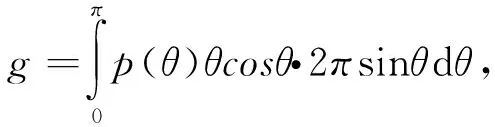


3 结论

