CoFeCrGa1-xAlx合金的电子结构、磁性和自旋零带隙半导体特性研究
方 旭,卢志红,李斯阳
(1.武汉科技大学材料与冶金学院,湖北 武汉,430081;2.武汉科技大学省部共建耐火材料与冶金国家重点实验室,湖北 武汉,430081)
自旋电子学是将电子自旋作为信息载体,利用自旋以实现数据存储、逻辑运算、量子计算等的一门新兴技术[1]。与传统半导体器件相比,基于电子自旋设计的器件具有非易失性、数据处理速率快、功耗低及集成密度高等优点[2]。为了实现对电子自旋的操控,需要材料具备高的自旋极化率,同时,其还需与现有半导体兼容[3]。自旋零带隙半导体(spin gapless semiconductor,SGS)理论上兼具100%自旋极化率与半导体特性,其在自旋向上方向价带顶部和导带底部于费米面处接触,为零带隙,自旋向下方向则在费米面处存在带隙。SGS可看作是零带隙半导体与半金属铁磁体的结合,具有如下优势[4]:①电子从价带激发到导带不需要克服能量势垒;②激发载流子的自旋极化率为100%;③载流子迁移率是传统半导体的2~4倍;④利用霍尔效应,可以实现极化的自旋载流子分离;⑤可通过施加栅极电压来控制费米面的移动,从而实现对载流子浓度的调控。自旋零带隙半导体对外部影响因素(如压力、电场、磁场、电磁辐射、杂质等)非常敏感,这使得该材料在自旋注入、自旋探测器、自旋发光二极管等领域具有广阔的应用前景。
自旋零带隙半导体最早是由Wang[5]在计算稀磁半导体PbPO2的能带时提出的,但稀磁半导体的居里温度较低[6],很难在实际中得到应用。而Heusler合金由于具有高的居里温度和自旋极化率而广受关注,其中Mn2CoAl[7]、Ti2MnAl[8]、CoFeMnSi[9]等Heusler合金被实验证实是自旋零带隙半导体。Bainsla等[10]从理论和实验角度证实了Heusler合金CoFeCrGa是一种自旋零带隙半导体,但CoFeCrGa自旋向下能带的带隙较窄,其费米面位于价带顶边缘,并且基于自旋零带隙半导体器件的使用温度范围取决于其自旋向下的带隙[4],而CoFeCrCa的窄带隙限制了其应用。Xu等[11]和Ozdogan等[12]通过理论计算预测CoFeCrAl是自旋零带隙半导体材料,并且其自旋向下能带的带隙较宽,因而可以通过原子掺杂来调控费米面在能带结构中的相对位置[13-14],而用Al原子取代部分Ga原子,理论上可增大CoFeCrGa自旋向下能带的带隙,同时将费米面调节至带隙中间,在保证自旋零带隙半导体特性的同时提高其半金属稳定性。
1 模拟计算方法
四元Heusler合金CoFeCrGa的晶体结构为LiMgPdSn型,化学式可表示为X1X2YZ,空间群为F-43m,其由4个面心立方晶格相互嵌套而成,在Wyckoff坐标系下,X1(Co)处于(0,0,0)位点、X2(Fe)处于(0.5,0.5,0.5)位点,Y(Cr)处于(0.25,0.25,0.25)位点,Z(Ga)处于(0.75,0.75,0.75)位点。分别用0、1、2、3个Al原子替代四元Heusler合金CoFeCrGa中的Ga原子,得到CoFeCrGa1-xAlx的晶体结构如图1所示,对应的Al掺杂浓度x依次为0、0.25、0.5、0.75。

(a)x=0 (b)x=0.25 (c)x=0.5 (d)x=0.75
本研究基于密度泛函理论(DFT)的第一性原理,采用VASP软件进行模拟计算,用Perdew-Burke-Ernzerhof(PBE)[15]定义交换关联函数,用投影缀加波方法(PAW)[16]描述离子实和价电子的相互作用。以Co(3d74s2)、Fe(3d64s2)、Cr(3d44s2)、Al(3s23p1)、Ga(4s24p1)为价电子组态,平面波截断能设置为550 eV,总能量收敛标准为10-6eV,原子间作用力不超过0.1 eV/nm,结构优化与静态计算使用15×15×15的K点网格精度,在此基础上再使用23×23×23的K点网格进行非自洽计算。
2 结果与讨论
2.1 晶格常数
图2为CoFeCrGa1-xAlx合金晶格常数随Al掺杂浓度x的变化。由图2可见,随着x的增大,CoFeCrGa1-xAlx的晶格常数减小,这是由于Al的原子半径比Ga小,当Al掺杂浓度增加时,合金晶格常数也会相应减小。当x为0、0.25、0.75时,合金为立方结构(a=b=c);x=0.5时,合金为四方结构(a≠b=c)。当x=0时,晶胞中包含4个Ga原子(见图1(a)),x为0.25、0.75时,含Al(Ga)原子的平面在垂直于晶轴a、b、c方向的原子类型和数目是等同的,因而合金呈立方结构;但x=0.5时,原子在b轴上的排列不同于a、c轴,沿b轴,在b=0.25的(010)平面有两个Al和两个Cr原子,b=0.75的(010)平面有两个Ga和两个Cr原子,但沿a轴,在a=0.25或0.75的(100)面上有1个Al、1个Ga和2个Cr原子,沿c轴,在c=0.25或0.75的(001)面上有1个Al、1个Ga和2个Cr原子,所以当x=0.5时,合金呈四方结构。

图2 CoFeCrGa1-xAlx晶格常数随x的变化
2.2 形成能和结合能
为分析Al掺杂浓度变化对CoFeCrGa1-xAlx合金稳定性的影响,特对其形成能Ef和结合能Ec进行计算,结果列于表1中,Ef和Ec计算式为:
(1)
(2)

形成能Ef表示不同类原子从单质状态形成化合物所释放或吸收的能量,负形成能表明化合物可以合成,且其绝对值越大,表明化合物越易形成。结合能Ec是原子由自由状态的孤立原子形成化合物所释放的能量,结合能为负值表明物质能够稳定存在,晶体的强度、结构稳定性与结合能相关,结合能越小,晶体结构就越稳定。由表1可知,CoFeCrGa1-xAlx(x=0、0.25、0.5、0.75)合金具有负的形成能,表明材料易合成,随着Al掺杂浓度的增加,结合能减小,表明CoFeCrGa1-xAlx合金的结构稳定性逐渐增强。
2.3 磁性
表2列出了CoFeCrGa1-xAlx合金的总磁矩Mtot和各原子磁矩,其中MS-P表示根据Slater-Pauling规则计算得到的原胞总磁矩。由表2可见,总磁矩主要来源于Cr原子贡献;随着Al掺杂浓度x的增加,Co的磁矩变化很小,Fe的磁矩线性增大,Cr的磁矩线性减小,而Al、Ga的磁矩始终为很小的负值,由于Al与Ga有相同的价电子数,故掺杂前后合金总磁矩Mtot基本保持不变。另外,理论计算的总磁矩与S-P规则计算的原胞总磁矩(Mt=Zt-24,Mt为总磁矩,Zt为价电子总数)相符。

表2 CoFeCrGa1-xAlx各原子磁矩和总磁矩
2.4 电子结构
为分析CoFeCrGa1-xAlx合金的电子结构,计算得到其总态密度如图3所示。由图3可见,CoFeCrGa1-xAlx(x=0、0.25、0.5、0.75)系列合金均为自旋零带隙半导体。随着x的增加,费米面从价带顶向导带方向移动,带隙宽度逐渐增大,x为0.75时,费米面位于带隙中间,可见CoFeCrAl0.75Ga0.25在系列合金中半金属稳定性最佳。Rani等[17]基于第一性原理研究了Co1+xFe1-xCrGa(x=0、0.125、0.375、0.5)系列合金后发现,当x<0.375时,Co1+xFe1-xCrGa保持自旋零带隙半导体特性,当x≥0.375时材料转变为半金属。由此可见,掺杂和改变成分比例可在一定范围内保持材料的自旋零带隙半导体特性。
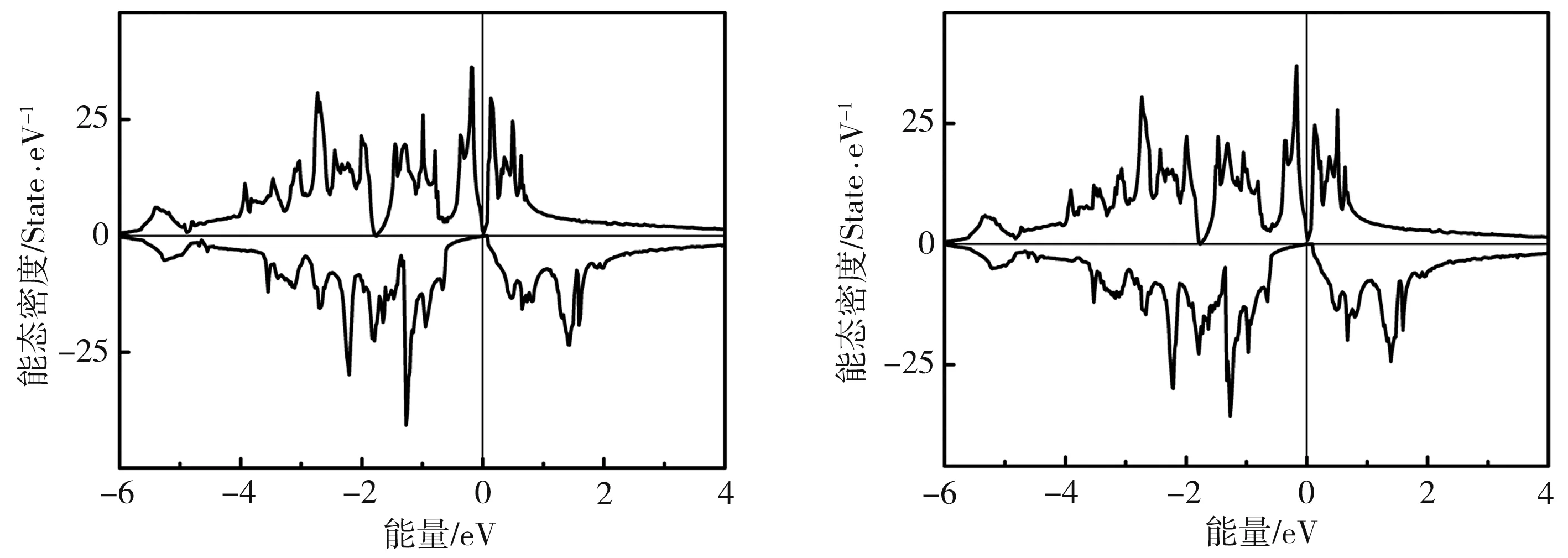
(a)x=0 (b)x=0.25
为更好地说明CoFeCrGa1-xAlx合金总态密度中各轨道的贡献,计算得到CoFeCrGa1-xAlx合金的分波态密度图如图4所示,由于-6 eV以下,能态密度贡献主要来自于Al或Ga原子的s电子,因其对总态密度的贡献很小,在图中并未给出。由图4可见,-6~-4 eV之间,Al或Ga的p电子与过渡金属3d电子轨道发生了p-d杂化,填充了其中的能态;而在-4~2 eV之间,态密度峰的贡献主要来自于Co、Fe及Cr的3d电子轨道杂化作用。对于自旋向上能带,Co、Cr原子在费米面以下分别形成较高的杂化劈裂峰,相对于Co原子,Cr原子形成的杂化劈裂峰更强,意味着总磁矩主要来源于Cr原子的贡献,这与前文磁矩的计算结果相符。Fe原子交换劈裂程度较低,其原子磁矩较小,但其交换劈裂作用逐渐增强,因而其原子磁矩逐渐增大。Cr原子在自旋向下能带中,由于交换劈裂作用减弱,反成键峰向费米面以下区域移动,使得Cr原子磁矩逐渐减小。自旋向下能带的带隙由Co原子与Fe原子的d-d电子轨道杂化作用决定,随着x的增加,Co原子与Fe原子间的d-d电子轨道杂化作用增强,使得Co、Fe的成键态峰向低能态移动,反键态峰则被推向高能态,导致带隙变宽。
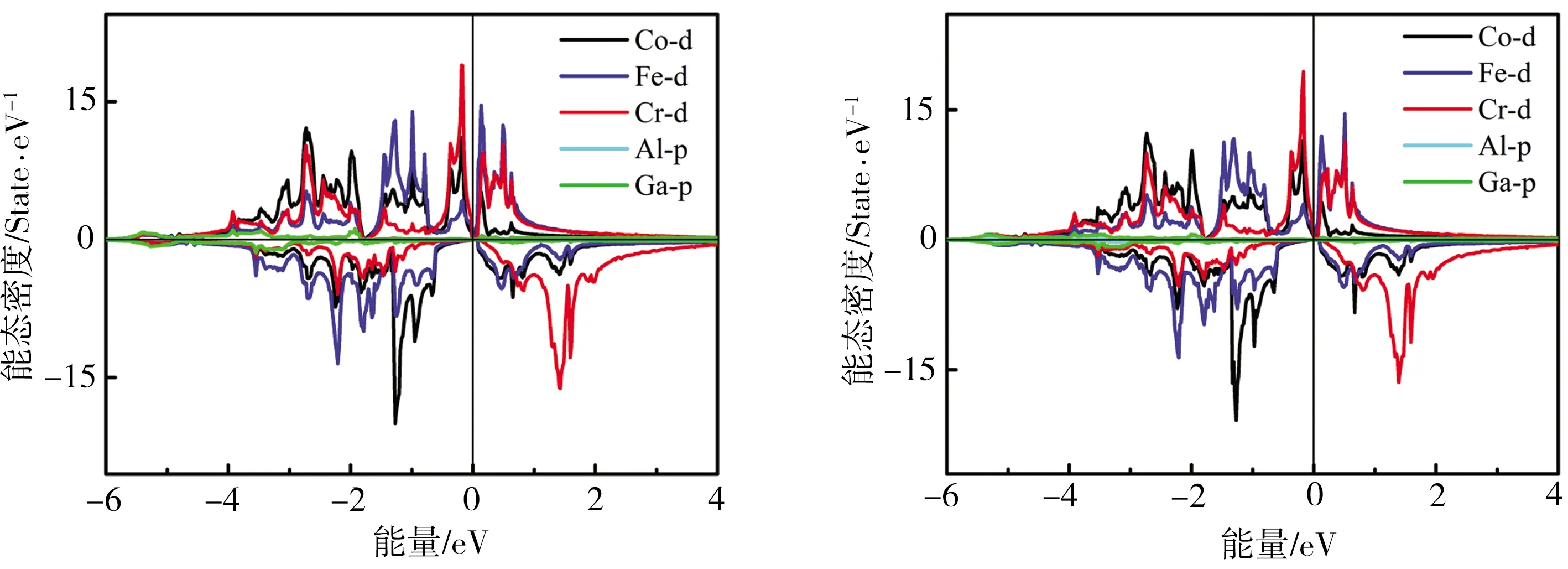
(a)x=0 (b)x=0.25
CoFeCrGa的轨道杂化模型如图5所示,其中,d1、d2、d3、d4、d5分别代表dxy、dyz、dxz、dx2-y2、dz2轨道,dxy、dyz、dxz轨道组成三重简并的t2g轨道,dx2-y2、dz2轨道组成两重简并的eg轨道。Galanakis等[18]在研究Co2MnGe的电子结构时提出了轨道杂化模型,即自旋向下能带的带隙由次近邻的Co原子间的3d电子杂化作用决定。CoFeCrGa合金中,Co原子位于次近邻Fe原子形成的八面体晶体场中,因此Co原子和Fe原子中简并度和对称性相同的轨道发生杂化,形成成键态eg、t2g轨道和反键态eu、t1u轨道。Co-Fe原子所形成的eg、t2g杂化轨道再与Cr原子的eg、t2g轨道杂化,形成了成键态eg、t2g轨道和反键态eg、t2g轨道,其中成键态位于费米面以下被电子填充,反键态位于费米面以上而未被电子填充,由于 Co-Fe杂化形成的反键态eu、t1u轨道与Cr的3d轨道不在同一表象,不能发生杂化。自旋向下能带的带隙由Co-Fe原子杂化形成的eu、t1u之间的能量差决定。对于自旋向上能带,交换劈裂导致所有能级向下偏移,当成键态2eg底部与反成键态2eu顶部相接触时,则形成了零带隙特性。

(a)自旋向上
Al掺杂虽然不直接参与Co、Fe及Cr原子的轨道杂化,但可间接引起费米面的移动和带隙宽度的改变,推测这可能与RKKY相互作用有关[19]。RKKY理论指出,由于sp电子是可以传导的,其与局域的d电子之间存在波函数的重叠而产生交换作用,这种交换作用会导致sp电子发生自旋极化,自旋极化的sp电子又会与另外相邻的局域d电子产生直接交换作用,不同的局域d电子分别与sp电子产生交换作用,sp电子相当于桥梁,将不同的局域d电子相互关联,实现不同局域d电子间的间接交换,间接影响Co、Fe及Cr原子之间的3d电子杂化作用,因而Al掺杂可以实现改变费米面位置、调节带隙宽度的目的。而sp-d之间的作用会导致sp电子和d电子之间反铁磁耦合,在计算中Al、Ga原子的磁矩始终为负值,与Co、Cr原子间的磁矩为反铁磁排列,表明该合金的磁矩符合RKKY机制。
2.5 四方形变
自旋零带隙半导体是以薄膜形式应用于自旋电子器件中的,但其与衬底材料的晶格常数不同,通常会存在晶格失配,在界面处产生较强的应变而引起四方形变[20],导致费米面发生偏移,影响合金自旋零带隙半导体特性,故需要分析四方形变c/a对CoFeCrAl0.75Ga0.25自旋零带隙半导体特性的影响。图6为不同c/a下CoFeCrAl0.75Ga0.25的总态密度图,可以看出,当c/a为0.99、1.01时,CoFeCrAl0.75Ga0.25保持自旋零带隙半导体特性;而c/a为0.95、1.05时,费米面处自旋向上能态出现部分态密度,合金失去零带隙特性,c/a=0.95时,费米面位于自旋向下的带隙之间,此时由自旋零带隙半导体转变为半金属,c/a=1.05时,费米面位于价带顶以下,合金失去半金属性。

(a)c/a=0.95 (b)c/a=0.99
3 结论
(1)随着Al掺杂浓度x的增加,CoFeCrGa1-x-Alx合金晶格常数减小,当x为0、0.25、0.75时,合金为立方结构(a=b=c),当x=0.5时,合金为四方结构(a≠b=c)。
(2)CoFeCrGa1-xAlx(x=0、0.25、0.5、0.75)具有负的形成能,表明系列合金易合成,且随着x的增加,合金结合能减小,合金的结构稳定性逐渐增强。
(3)随着Al掺杂浓度的增加,Co的磁矩几乎保持不变,Fe的磁矩线性增加,Cr的磁矩线性减小,Al与Ga的磁矩始终在很小的负值附近,总磁矩符合Slater-Pauling规则。
(4)CoFeCrGa1-xAlx(x=0、0.25、0.5、0.75)系列合金均为自旋零带隙半导体。在自旋向下能带,随着x的增加,费米面从价带顶向导带方向移动,带隙逐渐增大,当x=0.75时,费米面位于带隙中间,即CoFeCrAl0.75Ga0.25在系列合金中半金属稳定性最佳,在受到一定程度四方形变时,其仍能保持自旋零带隙半导体特性,是具有潜力的自旋电子学新材料。

