大孔径静态干涉成像光谱仪径向畸变导致的谱线偏移误差的校正

安玲坪，王 爽 ，张 耿，李 娟，刘学斌

（1.中国科学院西安光学精密机械研究所光谱成像技术重点实验室，陕西 西安 710119；2.中国科学院大学 北京 100049）

1 引言

成像光谱仪可同时获取目标的二维空间信息和一维光谱信息，具有“图谱合一”的特点，在目标特性检测、空间遥感以及气象探测等领域有重要应用[1-5]。20 世纪80 年代后期出现的无动镜干涉成像光谱技术[6-7]，为实现轻小型、高稳定性干涉成像光谱仪打下了基础。大孔径静态干涉成像光谱仪（Large Aperture Static Imaging Spectrometry,LASIS）出现于90 年代末[8]，无狭缝和运动部件，高通量和高稳定性的优势并存，是实现高光谱成像的重要途经[9]，有着广阔的应用前景。为获得高质量的光学信息，光学系统通常只在近轴区域，即小视场角成像。随着遥感仪器的进一步发展及数据实时性要求的不断提高，增大光谱仪器的视场角已成为一种趋势。

LASIS 面阵探测器包含多个探测单元，当视场角增大时，单次成像包含更多目标信息，可有效减少扫描次数，提高工作效率的同时还可以减少目标随时间变化导致的误差。但是图像边缘的畸变效应也会更加明显，探测单元的离轴角会使光程差改变[10]，此时干涉图像存在径向畸变导致的误差，使得最终复原后光谱图两边相对于中间谱线位置发生偏移，有研究表明这种现象会影响辐射定标精度[11]。谱线偏移后需要对光谱定标系数进行修正，且光谱定标对辐射定标影响很大。因此，校正径向畸变导致谱线偏移产生的误差非常有必要。

在实验室光谱定标过程中采用小视场多次定标的方法可实现精准定标，但是该方法大幅度降低了定标的工作效率，且随着成像光谱仪视场的增大，该方法很难满足实际工作需求。现有的畸变校正方法多为直接校正探测器采集到的信号[12-14]，这些方法并不适用于LASIS 探测器接收到的干涉图，但是通过校正反演光谱可以实现间接校正。本文在分析LASIS 的工作原理及光谱反演过程的基础上，提出了通过探测器畸变数据获得反演光谱偏移率，进而修正光谱定标系数的方法。最后结合实验室定标数据证明了本方法能够有效校正LASIS 光谱定标误差，改善数据质量。

2 误差校正方法的理论分析

LASIS 主要有前置光学系统，干涉系统，傅立叶成像系统和探测器4 个部分[8,15]，结构如图1所示。LASIS 光学系统是普通照相系统的前置镜，没有狭缝限制，能够实现高光通量，能量利用率高，具有大孔径优势。利用Sagnac 横向剪切干涉仪产生光程差，不需要运动部件，系统简单，稳定性高。面阵探测器可获得一维空间的干涉信息强度，再通过主动或被动推扫即可获得另一维空间信息。

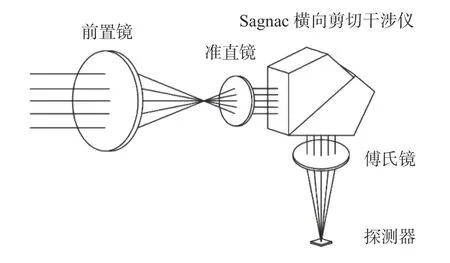
图1 LASIS 结构示意图Fig.1 Schematic diagram of LASIS structure

LASIS 干涉系统原理如图2 所示。傅氏镜焦距为fF，某一像点S被Sagnac 干涉仪剪切成在垂直于光轴方向相距d的2 个虚像S1、S2，视场角为α的两束平行光通过傅氏镜后，在成像面处汇聚到与光轴相距y的一点，此时存在光程差x，从而发生干涉[16]。

图2 LASIS 干涉原理示意图Fig.2 Schematic diagram of LASIS interference

LASIS 测量目标光谱辐射的干涉信息，可通过数学计算方法利用变换的方式反演出目标光谱。光谱强度与干涉强度是傅立叶变换对，关系式如下：

式中，x为光程差，υ为波数，I为干涉强度，B为光谱强度。理想情况下光程差x可以取到无穷大来反演完整的目标光谱B，但是受光学系统和探测器尺寸限制，在干涉图采样过程中无法将光程差取到无穷大，令截止频率为L，得到的干涉图为：

对于每个探测器像元，得到的信号强度是一定范围的积分，探测器像元(i,j)采集到的待测目标像元i的第j个光谱通道的辐射信号为：

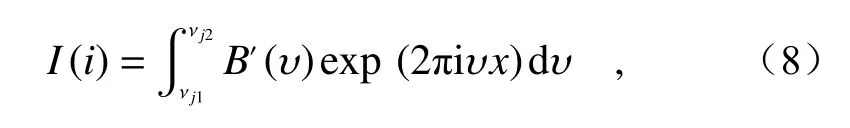
式中，νj1和 νj2表示探测器像元(i,j)包含的最小和最大波数。

当视场角增大时，垂轴放大率会随之改变，成像面干涉图的径向畸变无法忽略，且畸变程度与像元位置到畸变中心的距离的平方成正比。对于图像来说，径向畸变不会改变清晰度，但是会改变图像的几何位置[18]，图2 中两束相干光的汇聚点变为：

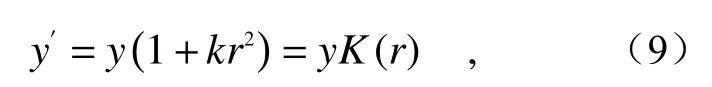
式中，k为径向畸变二次项系数，k=0时无畸变，k>0时为正畸变，即桶形畸变，k<0时为负畸变，即枕形畸变，畸变效果如图3 所示。

图3 径向畸变效果图Fig.3 Diagram of the radial distortion effects

此时，两束光线的光程差为：

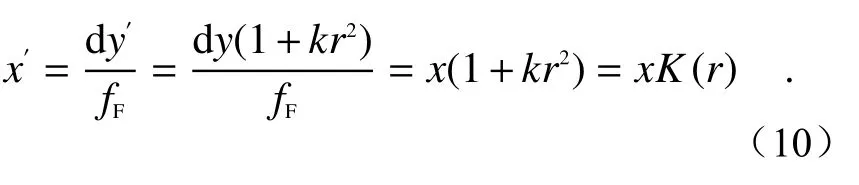
光谱强度与干涉强度是傅立叶变换对，根据傅立叶变换的尺度变换性质，发生径向畸变后的干涉图对应的反演光谱谱线位置会发生偏移，且偏移程度与畸变程度和像元位置有关：

若在进行光谱定标时，将谱线偏移产生的影响包含在定标系数之中，便可以减弱畸变导致的误差，修正谱线位置，改善数据质量。谱线偏移带来的影响可用偏移率表示，将每一条反演光谱原本的定标系数除以该条谱线的偏移率便可校正径向畸变所导致的光谱定标误差。

3 仿真分析与校正模型

选取脉冲谱作为目标光谱，验证本文误差模型的正确性。脉冲信号δ(υ)与常数1 是傅立叶变换对，根据傅立叶变换频移性质，中心波数为 υ的脉冲谱δ(υ−υ0)的干涉曲线为e−jxυ0的实数部分，即脉冲信号的干涉图为余弦曲线。

本文首先利用Matlab 软件对探测器采集信号的过程进行仿真，然后编写程序对数据进行处理，即将干涉数据反演为光谱数据，具体流程如图4 所示。

图4 仿真试验流程图Fig.4 Flow chart of the simulation experiment

余弦曲线由Matlab 软件生成，面阵探测器可同时采集多个目标的干涉曲线，将余弦曲线进行复制，并代入式（9）模拟径向畸变过程，得到待采样干涉图。由于Matlab 的数据是由离散的点组成的，因此m与n的取值要尽可能大才能更接近实际的连续信号。接着，将图像分割成整齐分布的矩形区域，并根据式（8）对矩形区域进行积分，获得待处理干涉数据，为与下文实际的探测器像元数目一致，M取256，N取2 048。根据干涉曲线光谱反演的过程[19]编写数据处理程序，遍历所有干涉曲线得到最终的光谱图。

由于LASIS 的有效谱段为可见—近红外范围，同时为了与实验室光谱定标过程相匹配，本文选用了中心波长分别为400、543、632、694 和900 nm 的5 种脉冲信号模拟目标光源。一般成像光谱仪的畸变都在4%以内[10]，本文分别模拟了无畸变以及畸变率K为1%，2%和3%的桶形畸变与枕形畸变，最终得到每一列谱线峰值波数相对于中心列谱线（无畸变）峰值波数的偏移率P，如图5（彩图见期刊电子版）所示，6 种线型分别代表6 种脉冲信号，不同的畸变率用不同颜色表示。

可以看出，偏移率P随畸变率K和像元位置的改变而改变，同种颜色的曲线近似重合在一起，偏移率P与波长相关性较小，可认为与波长无关。理论上，偏移率为连续曲线，但是经过矩形采样后，采集到的信号为离散信号，加之Matlab 程序计算偏移率的精度为0.001，因此出现了跳变。仿真实验结果显示，径向畸变对反演谱线的影响可以用谱线偏移率表征，偏移率是与波长无关，与像元位置有关的二次曲线，5 种脉冲信号在畸变率相同时，偏移率变化趋势基本一致，通过拟合可得：

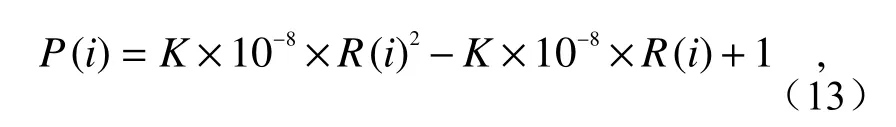
式中，K表示畸变程度，K%为畸变率，R(i)为探测器像元i与畸变中心O之间的距离，R(i)=|O−i|。

图5 Matlab 模拟结果Fig.5 Matlab simulation results

根据所得畸变模型，任意目标点i的第j个谱段中心波数υ(i,j)以及中心波长λ(i,j)的径向畸变误差可通过如下方法进行校正：

4 验证实验与结果分析

为了验证本文所提误差校正方法的性能，本文进行了实验室光谱定标实验，采集了LASIS 探测器的干涉信息，通过进一步的光谱反演处理，确定了不同像元的光谱定标参数（单位光程差和最大光程差），为谱线校正提供了初始光谱定标依据。

图6 为实验室光谱定标实验原理图，定标光源为标准激光器，利用激光器获得特定中心波长的光束，单色光经过扩束整形后照亮平行光管靶面处的毛玻璃，通过平行光管转换成光谱定标所需的平行光。平行光进入LASIS 光学系统后最终在探测器上形成干涉图，利用数据采集软件实现图像采集和存储。最后使用数据处理软件根据图4 中光谱反演部分的流程对干涉图进行数据处理并分析。

图6 光谱定标实验示意图Fig.6 Schematic diagram of the spectral calibration experiment

LASIS 探测器面阵大小为256（光谱维）×2 048（空间维），标准激光器发出的光束无法覆盖探测器空间维整个视场，所以分3 次分别在左、中、右3 个位置进行成像实验。畸变数据利用平行光管对LASIS 探测器进行一维内方位元素标定（空间维）获得。经过成像和拟合，得到探测器采集到的图像为正畸变，畸变中心在第1 070 列，即O=1 070，畸变率为0.3%，即K=0.3。代入式(13)得到该探测器各列像元反演光谱的偏移率为：

实验分别记录了594.1 nm 激光器和632.8 nm激光器成像实验的干涉图像，以及有效像元的反演谱线。图7 展示了实验获得的干涉图像，图8（彩图见期刊电子版）绘出了不同视场归一化后的反演谱线。从图8 可以看出当存在桶形畸变时，两侧谱线的峰值波长向波长增大的方向发生了偏移。

图7 激光干涉图Fig.7 Interferogram of the lasers

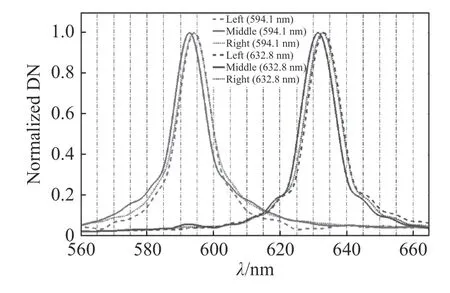
图8 激光三视场归一化反演光谱Fig.8 The normalized inversion spectra of the three fields of view of the lasers

对每一条反演光谱通过高斯拟合得到峰值波长，并利用式（14）、式（15）进行谱线校正。图9（彩图见期刊电子版）绘制了误差校正前后有效成像区域反演光谱的中心波长，表1 列出了部分数据结果。

图9 光谱定标误差校正Fig.9 Correction of spectral calibration

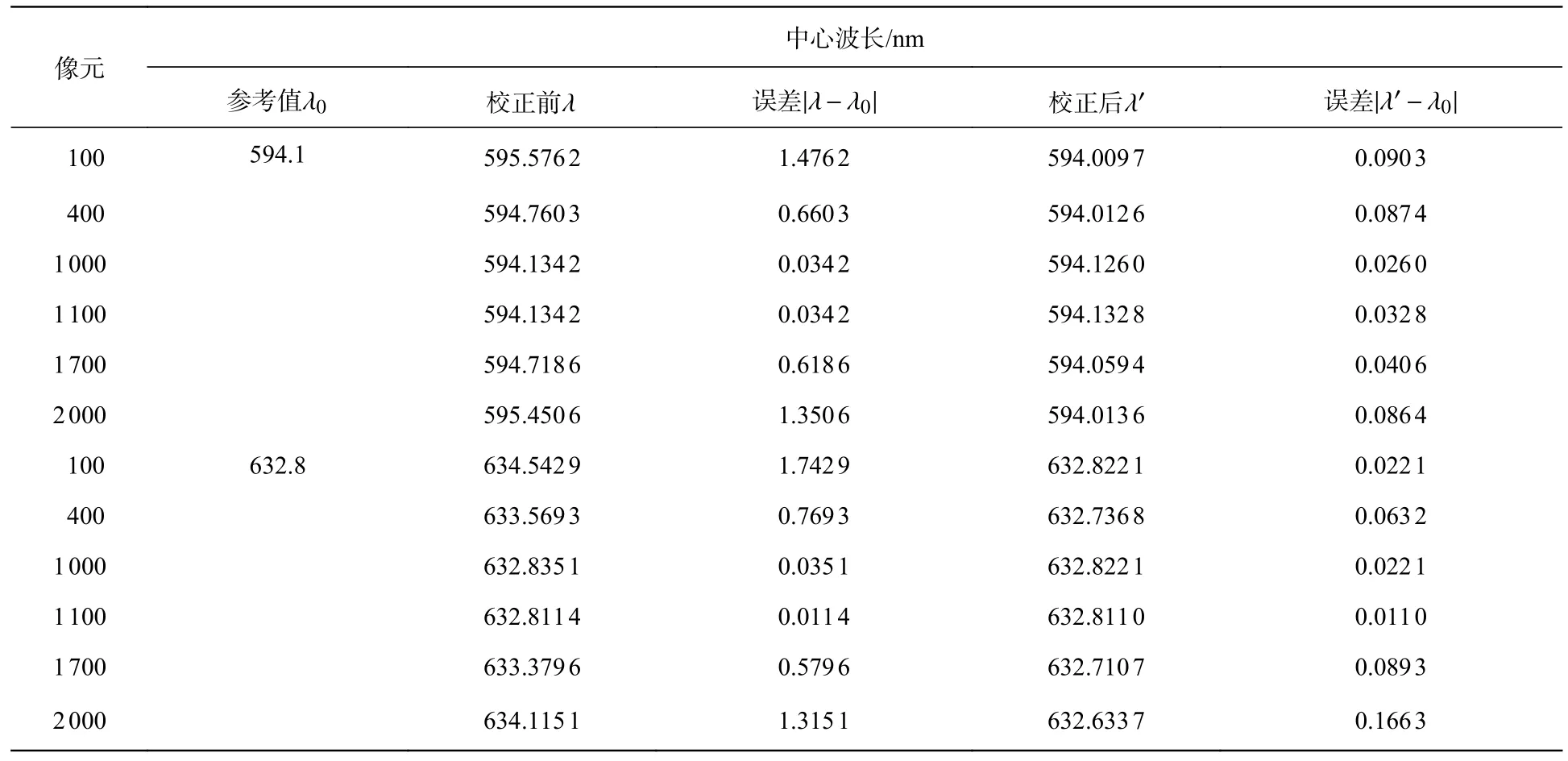
表1 激光中心波长对比Tab.1 Comparison of the lasers’center wavelength

从图9 和表1 可以看出，随着与畸变中心距离的增大，中心波长向长波方向移动，但偏移量与距离不成线性关系。校正前中间误差较小，两侧误差较大，序号为100 和2 000 的像元中心波长的误差均大于1 nm。利用本文的校正方法进行处理后，整体的误差得到了显著降低，图9 中红线与绿线基本重合，由表1 可知，除632.8 nm 右视场边缘外，误差均小于0.1 nm。632.8 nm 在右视场的校正效果略差的原因可能是由于探测器在安装过程中出现了倾斜、旋转等，使得实际畸变分布不是理想的桶形畸变[20]，进而导致了误差。实验证明，本文提出的谱线位置误差校正方法具有较好的校正效果。

为了验证该误差校正方法在红外波段的有效性，本文利用LASIS 进行了室外推扫实验，并选取一帧图像进行光谱反演，分析了不同像元位置处氧气在红外波段的吸收带。分别选取了左中右3 个视场序号为100、400、1 000、1 100、1 700 和2 000 的复原光谱，将746～779 nm 光谱曲线进行归一化处理后，得到的氧气吸收带如图10（彩图见期刊电子版）所示。可以看出两侧视场存在纳米级的偏移，经过校正后，吸收带曲线更加聚集，表明该误差校正方法在近红外波段依然有效。

图10 氧气红外吸收带Fig.10 Absorption band of oxygen in infrared wavelengths

5 结论

本文提出了一种径向畸变误差校正模型以校正光谱反演时出现的谱线偏移，用于大孔径静态干涉成像光谱仪在使用大面阵探测器时的光谱定标。根据干涉图与光谱图之间的对应关系和径向畸变的理论和数学表达式推导出了径向畸变与谱线偏移的模型，用计算机仿真实验验证模型，并给出了误差校正模型，最后实验验证了模型的准确性和可靠性。实验结果表明，本文所提出的校正方法可以有效减少谱线误差，对于594.1 nm 激光，边缘视场的谱线误差从1.5 nm 减少到0.1 nm，对于632.8 nm 激光，尽管右边缘误差校正效果相对较差，但是也减少到了0.2 nm，在近红外波段也有明显校正效果，表明该方法准确可靠，提高了数据质量。尽管该方法是基于干涉型成像光谱仪实验室光谱定标提出的，但当仪器投入使用后，畸变数据可以通过载荷的外方位元素进行修正，从而光谱定标误差也可以不断校正，实现再定标，该方法具有长久的参考价值。