基于多激光传感器装配的自由曲面法线找正方法研究

张 赢，丁红昌,2，赵长福，周义根，曹国华,2

（1.长春理工大学机电工程学院，吉林 长春 130022；2.长春理工大学重庆研究院，重庆 401135）

1 引言

目前，自动钻铆技术已被众多学者关注，这一技术在国产化、技术自主化的大型飞机项目上，更显得极为重要[1]。通过对该领域的调研不难看出，自动钻铆机器人的先进程度和航空业发展程度息息相关，例如：美属捷姆科公司(GEMCOR)[2]、德国的宝捷公司（BROETJE）[3]等，都拥有自主研发的先进自动钻铆技术。以德国BROETJEAUTOMATION 公司为例，其所研发的RACE 自动钻铆系统，得到了市场的一致认可，该机器人是基于法线方向以及基准面进行检测的，因此，可以达到准确定位的更高目标[3]。2019 年，德国FILL 公司研发的ACCUBOT 自动钻铆机器人是一个数控7 轴机器人，它将末端执行器移至处理器提供的钻孔位置后，激光传感器可自动检查部件和钻孔的对准情况，并在必要时重新调整。近些年，国内高校、科研机构和飞行器制造厂商开展了大量研究[4-10]。北京航空航天大学的公茂震团队，应用末端垂直度智能调节法对机械手位姿进行调正[11]。该方法利用三维激光扫描仪对自由曲面进行检测，再通过二元角度调节法调节钻头的角度，但该方法检测效率较慢，只适合离线检测。研究人员战强等提出了“手眼标定”方法[12]。该方法利用相机坐标系和场景坐标系之间的关系，计算出手眼的相对位置及坐标点的空间位置，并将信息传入至机械手，从而大大减少了计算量，但其位姿检测精度不高。沈阳飞机工业（集团）有限公司研制出一整套应用机器视觉技术开发的平面工件检测系统[13]。该系统可以同时检测焊缝和钻铆孔位的信息及相对位置，并将其传递给上位机，上位机根据这些信息实施控制。由于该系统要求摄像机的工作距离与“手眼标定”时摄像机的工作距离完全相同，所以在对自由曲面进行法向标定时，有一定的局限性。针对以上问题，本文提出了一种基于多个激光传感器的非接触法线测量找正方法，该方法适合自由曲面的法线检测并对系统误差进行了有效补偿，在不损伤被测物体表面的前提下提高了检测精度及速度，对自动钻铆系统进行检测时，制孔机器人的垂直度是衡量其性能的主要指标，在一般情况下，这一指标是由钻铆系统的法向找正精度和激光传感定位精度所决定的。另一方面，机器人装备传感器在线在位工作时，必定会产生装配误差、磕碰、偏移等状况，大大降低了制孔定位的准确度，进而影响了装配精度和整个结构件的疲劳性能。因此，如何通过在线在位误差补偿方法提高自动钻铆系统中法线方向检测精度，最终提高连接孔的位置精度，成为一个重要的研究方向[14-17]。

2 多激光传感器装配的自适应法线找正系统

找正待测加工点实际的瞬时法线方向，需要多个位移或距离激光传感器，通过局部微小区域的实时测算，调整机器人的主轴轴线方向[18]。基于此，本文提出了应用多激光传感器装配的自适应法线方向找正法，可对传感器检测中发生的一系列系统误差进行有效补偿，从而提高定位精度，以达到其垂直度要求。

2.1 姿态找正的几何原理

标定系统把装置测算到的位移信息转化成安装了钻铆刀具的载具，建立了能够进行精确调姿的数学模型。工具坐标系中（θ1,θ2,0）的角度数据是由加工点外法向和钻孔刀尖轴线所建立的几何模型确定的，可用于钻铆加工中末端执行器的精确调姿，以提高法线检测精度。

从以上模型可以看出，当被加工点外法向和机器人钻孔刀尖轴线完全重合时，便可视其加工姿态已经找正[19]。图1（a）、1（b）中，P1、P2、P3、P4为激光位移传感器，而Q1、Q2、Q3、Q4为其投射点。要求对角线组成的平面相互垂直，否则需求解其夹角，其交线应为OT。TH为法线方向，其与OT夹角为θ。P1Q1=h1，P2Q2=h2，即P1P2=l12，为安装尺寸，同理P3P4=l34。读取传感器所显示的值：h1、h2、h3、h4。TN、TM为线段TO的投影。TO与TN、TM的夹角分别为θ1、θ2。由图1（a）可以看出θ与θ1、θ2、t1的关系，其中t1为TM与TN的夹角。θ的数值恒正，其为线 段TO与TH的夹角，而θ1、θ2、t1均为向量之间的倒角，有正负之分。现规定：θ1为正向，θ2为正向，t1的正负与θ1保持一致。如图1（c）所示，P1P2垂直于AQ1、BQ2，AQ1与P1Q1的夹角及BQ2与P2Q2的夹角均为λ。由此可得：

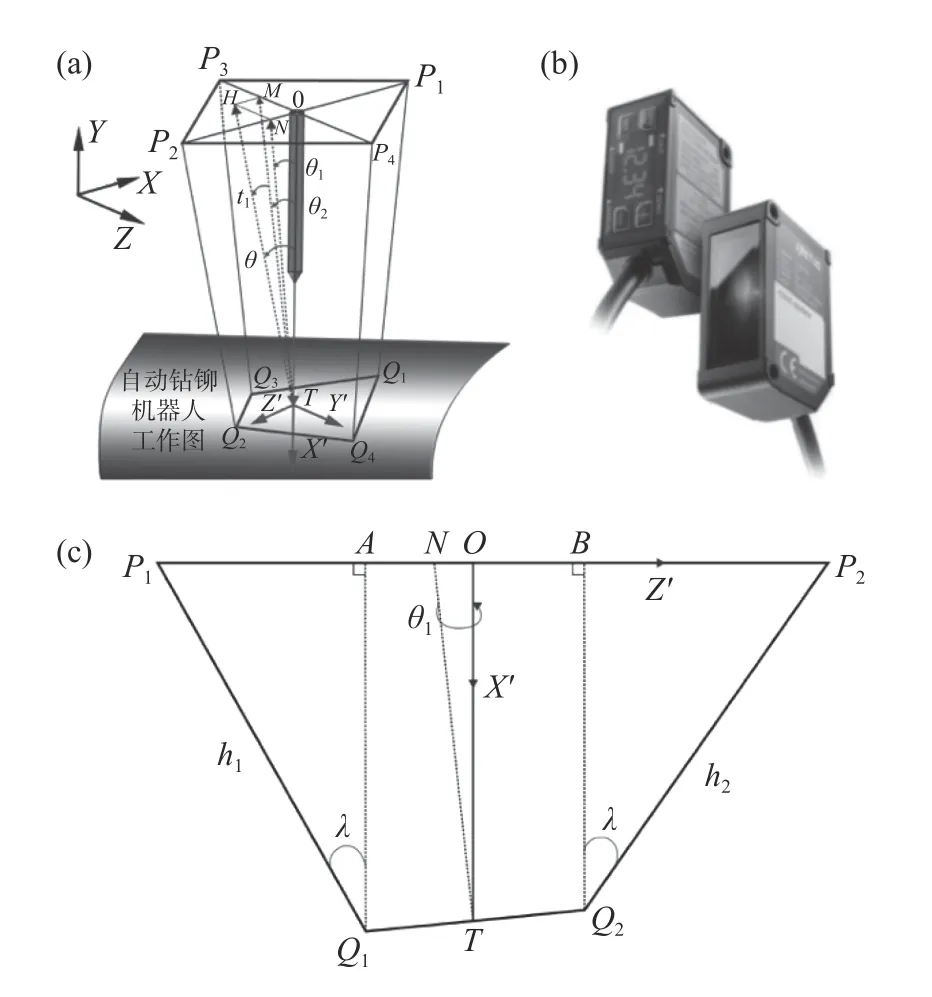
图1 （a）姿态找正模型；（b）使用的激光传感器型号：FASTU/CD22；（c）X'TZ'坐标平面内角θ1与h1h2之间的关系Fig.1 (a)Geometric model for posture alignment;(b)type of laser sensor used:FASTU/CD22;(c)relationships betweenθ1,handh2in theX'TZ'coordinate plane.

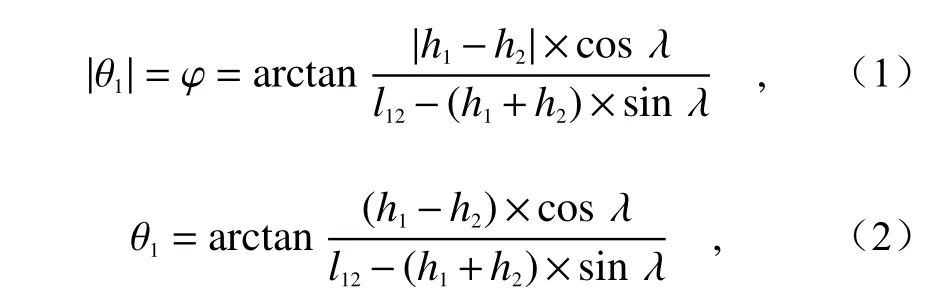
同理可得：

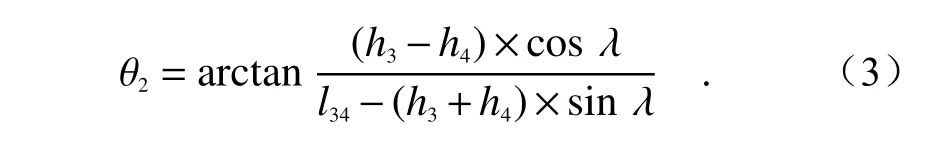
2.2 法线找正方法及数学模型

机器人在使用过程中难免会产生碰撞、偏移及装配误差等，通过对标定块的提前标定，可在系统中对误差进行有效补偿。对于补偿后的机器人，再利用特殊标定块（例如0°标定块）进行标定，确认已经准确补偿之后，再进行后续工作，以保证孔位的准确度，从而完成钻铆机器人在线位姿的自适应修正。

通过几何原理的推导过程可知，自适应找正方法的模型建立主要在于求取θ、t1与θ2、θ1之间的关系。将垂直度误差（被加工点外法向和机器人钻孔刀具轴线的夹角）分解为平面X′TY′与X′TZ′内的两个偏角，并建立该偏角和传感器测量值的数学模型，此时法向偏角θ1、θ2与位移传感器测得的数值（即h1、h2、h3、h4）之间有如下关系：

利用此数学模型求出法向偏角θ1、θ2以后，便可逆推出实际工作状况下机器人的法线方向。实验装置如图2 所示。具体步骤如下：①放置5°的标定块，读取h1和h2；②将法兰盘旋转90°，读取h3和h4；③替换成其他标定块，并记录相应数值；④代入式（4），解得Angle1、Angle2、l12。代入式（5），解得Angle3、Angle4、l34；⑤得到标定后公式；⑥放置0°标定块，读取传感器读数，代入式（2）和式（3），求得θ1、θ2。将θ1和θ2代入式（4），求得θ。用求得的θ与0°标定块的法向（即90°）相比，便可得到法线偏差值，用以验证。

图2 法向标定实验所用的设备。（a）激光传感器安装示意图；（b）标定块Fig.2 Equipments used in normal-direction alignment experiments.(a)Schematic diagram of the laser sensor assembly;(b)calibration blocks

3 误差分析和补偿方案

3.1 法线找正方法的误差分析

飞机的实际制孔过程中，在传感器安装、钻铆压头刀具装配时，存在误差[20]。制孔过程中的具体误差有：（1）传感器装配到工作法兰盘上之后，其检测光束与钻孔刀具轴线异面，存在的误差[21]；（2）钻头接触工作面时轴线和成对角存在的检测光束，这3 条线所围成测量面内的误差。

实验时，多个传感器的实际安装角度和理论安装角度之间存在误差，工作法兰盘加工情况和现场安装环境也会引起比较明显的误差。另一方面，成对安装的两个传感器之间（例如P1、P3或者P2、P4）的理论安装距离和实际安装距离（即l12与l34）也存在明显差异。本文将以上两个误差类型作为下一步补偿模型中主要解决的问题。

3.2 法线找正方法的误差补偿模型

本部分将通过自适应标定方式来补偿以上误差类型。具体步骤如下：建立工具坐标系T-xyz，并获得位姿；然后，分多次将各角度标定块置于T点处，4 个传感器所在平面和工作台平行，即标定块的法向与待测面的法向重合。由于h1～h4已知，Angle1～Angle4未知，同时l12和l34也需求解，据此列出关于h、Angle、l、θ的函数式。测算出3 组或3 组以上的已知数据，便可解算出以上未知量；最后，将0°标定块置于T点处，对精度进行验证。待机器人的相关检测参数合格后，即完成自适应调整之后，再进行被检测面法线方向的检测，以达到误差补偿的目的。标定后的法向偏角检测公式可修正为：

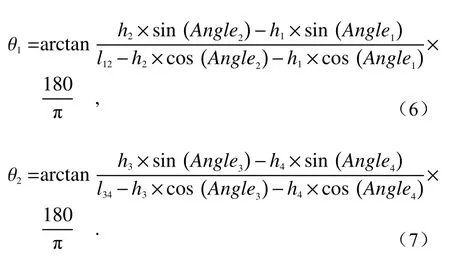
对于标定后的误差修正模型，可测得多激光传感器的精确安装角度：Angle1、Angle2、Angle3、Angle4。考虑到θ1的数值由h1和h2决定；θ2的数值由h3和h4决定，所以可分别进行求解。当传感器P1、P2的检测点在同一直线上时，利用余弦定理和前一步测得的实际安装尺寸，可计算出两组法兰盘相对传感器到测量零点的真实距离，即l12和l34。记录传感器的检测数值时，采用多次取值的方法，这样做是为了增加准确性。

3.3 基于经纬仪标定的误差分析及补偿

由于孔位信息需补偿从机器人制孔前段所产生的传递误差，才可以提高系统定位精度。一般飞机产品均有一定曲率，自适应找正方法的理论推导模型也都是在被测面为曲面的基础上进行的。

为了验证法线标定精度，需要在平面上使用经纬仪进行对标。由于只有在被测面的法线和经纬仪所测出的法线一一对应时，才可以对比相应的法线位置测算结果。前期研究，已经使用电子经纬仪检测过产品的空间角和平面的法线位置，以上均可作为现阶段工作的基础。

本文选择Leica 公司生产的工业电子经纬仪TM6100A，对本文方法确定的法线角度进行检测，测量精度可达0.5"，远远高于本次研究中对于法线位置的检测要求，所以可以用于验证实验中的误差补偿效果。本次实验中，采用标定后检测系统的相关数据，用以对系统中现场的法线变化量进行测量。经纬仪视觉瞄准系统所接收到的相对光强与被测镜面法线偏角之间的关系模型如下：

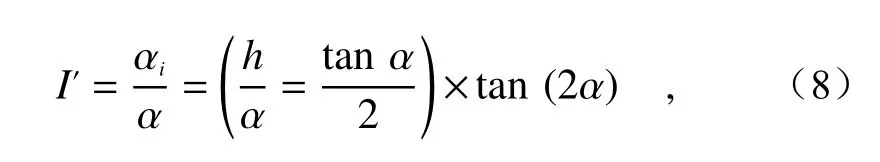
式中，h为视觉系统的工作距离；α为镜面反射的光线在光轴截面上的线性长度[22]。为验证自适应法补偿后的法线方向是否满足检测精度的要求，使用电子经纬仪和角动台对标定块的实际法向变化量进行测量，对实际法线方向变化量与理论变化量之间的结果进行对比。本文所构建的测试平台如图3 所示。

图3 法线检测验证平台。（a）验证平台装置图；（b）实验场景图Fig.3 Verification platform for detection in the normaldirection.(a)Experimental devices;(b)experimental scene

具体实验步骤如下：（1）将20°的标定块以任意方向放置在位置为0°的角动台平面上，并在其同一垂直平面内，固定一个立方镜，便于经纬仪确定角动台平面偏转的准确位置；（2）使用角动台将已固定好的标定块和立方镜依次转动大致相同的角度（如1°、0.1°等）；（3）使用电子经纬仪测得立方镜经角动台调节后的法线变化角度：Angle_act。因为立方镜和标定块已被固定在角动台的同一平面上，故可以认为立方镜的法线变化量与被测标定块的法线变化量相等；（4）重复步骤（3），按照实验时所需测试角度的固定单位变化量（如1°、0.1°等），重复多次操作，以提高实验精度；（5）将标定后系统计算出的法线变化量和经纬仪测量出的法线变化量进行比对，以判断法线方向的找正效果。基于C#语言，将第一阶段实验得出的位移传感器标定系数输入到编写的程序内，可以得出标定后系统计算出的法线变化量Angle_cal。同时根据步骤（1）～（4）得出的经纬仪测量空间姿态变化量数据，可计算出法线变化量Angle_act。将两个角度变化量的绝对值进行做差，就可得出找正偏差值abs_err，以此验证本次实验的找正误差精度。

4 实验验证和数据分析

4.1 基于多激光传感器装配的自适应找正方法的精度补偿实验

本次法线精度补偿模型的验证分两阶段。第一阶段是系统定位精度补偿验证实验，即对整个系统进行标定，并通过计算和误差补偿，从而验证实验系统定位精度。

在第一阶段实验中，检测装置包括：FASTU/CD22-35-485 型号的激光位移传感器，测量范围为20～50 mm，最高分辨率为0.002 mm，检测精度最高可达0.006 mm，绝对定位精度为±0.1%。法兰盘外径为80 mm，将安装角度定为45°。定制从0°到20°的自适应标定块组，其中每增加5°，定制一个相应角度的标定块。用“十”字线给投射点定位。对检测系统进行定位误差样本采集实验，获取式（6）和式（7）的数据源。本阶段的标定流程为：（1）记录数据，取多次平均值，确保数据的准确性，可得到工作法兰盘上的实际安装角准确信息：Angle1=44.430 9°，Angle2=44.374 8°，Angle3=44.374 8°，Angle4=44.430 9°；（2）将求得的实际安装角度信息代入到精度补偿公式（6）和式（7）中，得出实 际安装距离:l12=83.185 4 mm,l34=83.185 4 mm。第一阶段验证实验完成后，将以上所测数据再带回模型中，以使自适应标定补偿算法达到预期的定位精度。

4.2 法线找正精度验证实验

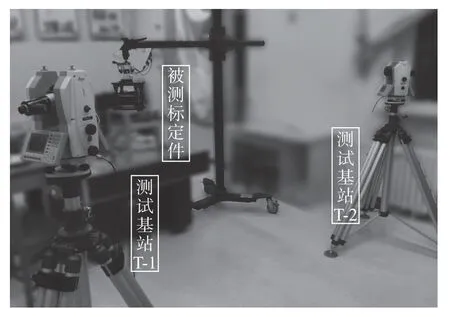
图4 法线找正实验设备Fig.4 Experiment setup of normal-directions alignment

为了测试本方法对法线方向找正的最大有效角度范围，采用前文所述方法，在不同角度下，对实验的测试结果进行了比对。以不同旋转角度进行多次测试（如2°/次、1°/次、0.2°/次、0.1°/次等），并整理了相关数据，以1°/次为例，实验测量数据如表1 和图5 所示。

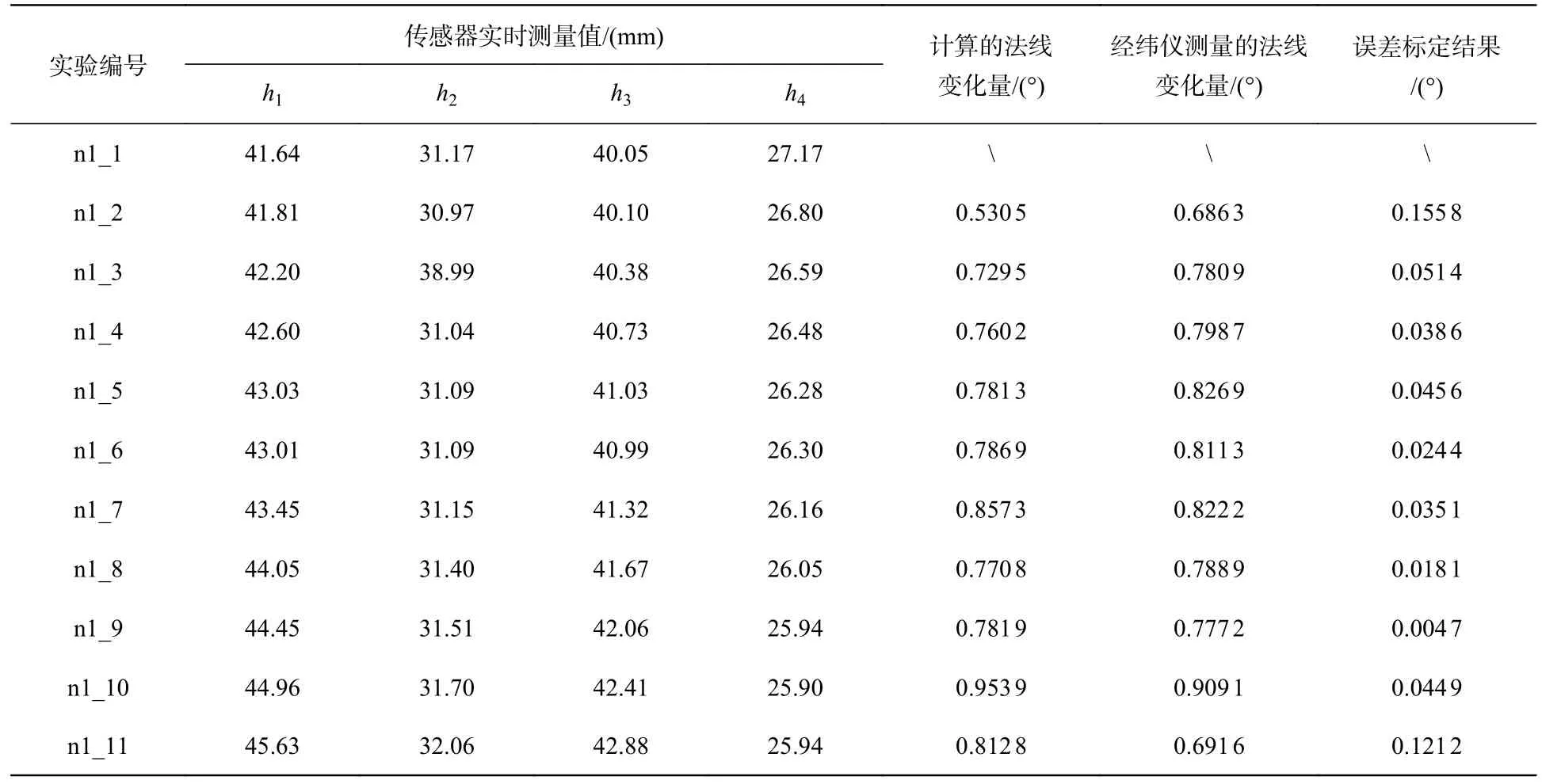
表1 转动角度为1°/次时法线找正实验验证数据Tab.1 Verification data of normal-direction alignment with rotation angle of 1°/time

经过验证实验，将测得的两组法线角度的变化量Angle_cal 和Angle_act 进行比对，即标定精度，或称为找正法线偏差值abs_err。表2 记录了在角动台上，以不同旋转角度进行测试时，实验的偏差值测量数据。目前对航天类装配孔的精度指标要求为制孔系统的法线角度偏差低于0.5°[23]。将得出的具体数据与目标标定精度0.5°进行比较，比较结果如图6 所示。

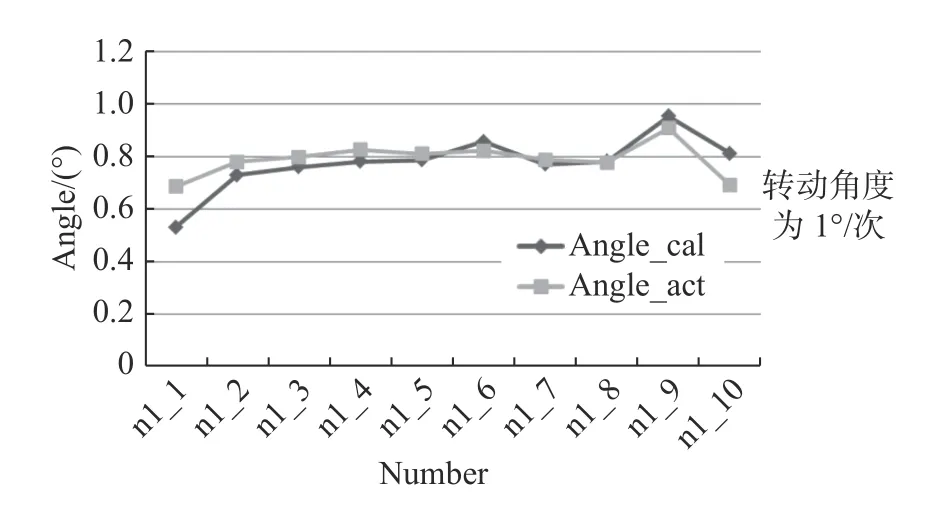
图5 转动角度为1°/次时，计算出的法线偏转角度和经纬仪测量出的偏转角度值分析Fig.5 Data analysis of the Angle_cal calculated and the Angle_act measured by theodolite(rotation angle is 1°/time)

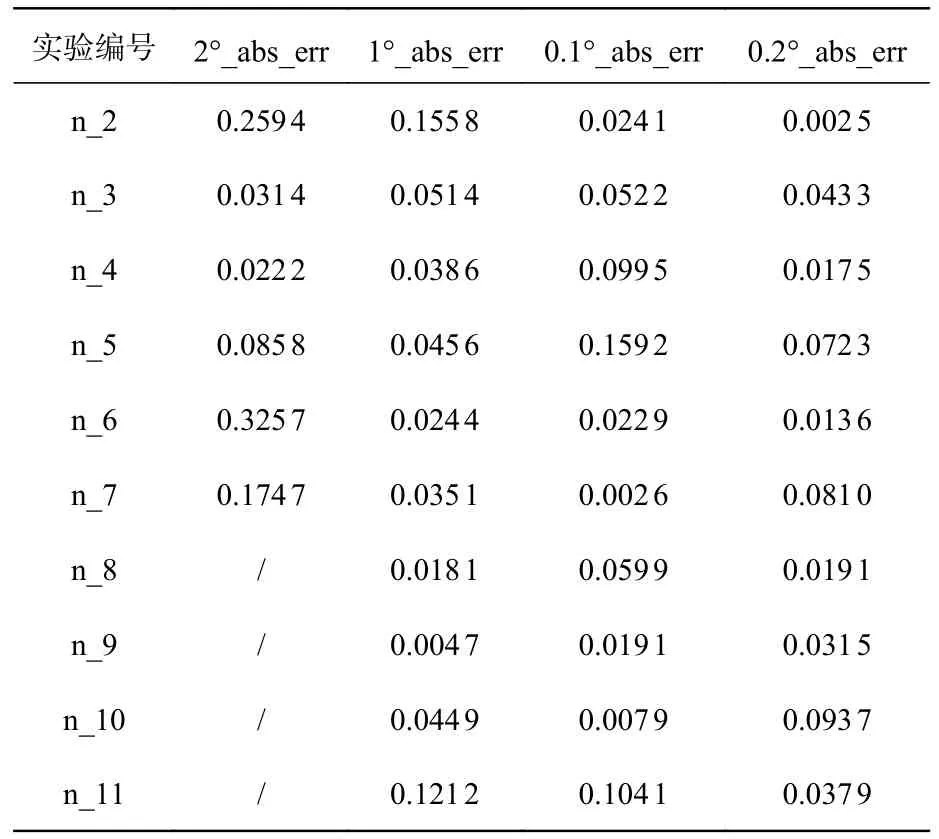
表2 验证实验后所统计的法线偏差值(abs_err)数据Tab.2 Statistical data of normal deviation value(abs_err)in validated experiments

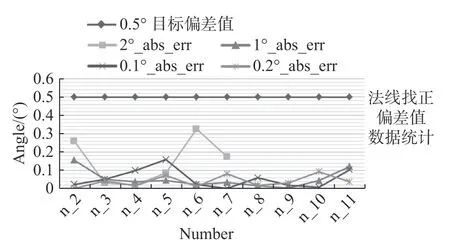
图6 法线检测偏差值与0.5°线进行比较Fig.6 Comparison of the normal deviation data with 0.5°target deviation

图5 所示的两个曲线基本重合，说明检测系统经过误差补偿后，在适合的标定面转动幅度下，与经纬仪所检测到的实际法线方向相比，具有较可靠且稳定的找正精度。

表2 说明，建立相关的模型及进行标定后：在角动台以2°/次的旋转角度进行测试时，其找正法线的最大偏差值abs_err 为0.325 7°，平均偏差值为0.149 9°；在角动台以1°/次的旋转角度进行测试时，其找正法线的最大偏差值为0.155 8°，平均偏差值为0.054 0°；在角动台以0.1°/次的旋转角度进行测试时，其找正法线的最大偏差值为0.159 2°，平均偏差值为0.055 1°；在角动台以0.2°/次的旋转角度进行测试时，其找正法线的最大偏差值为0.081 0°，平均偏差值为0.041 2°。测量数据的偏差值均在数据公差范围(0.5°)以内，这说明本文的误差补偿方法可以有效降低标定过程中的相关误差，提高了检测系统中的法向找正精度，且实验结果具有可重复性。

对比图6 中的数据统计曲线可知，在角动台以2°/次的旋转角度进行测试时，其平均偏差值为0.149 9°，当角动台调整的角度总和超过12°时，便无法在经纬仪中计算到法线位置，即Angle_act的值。同时，除以2°的旋转角度测试外，其余数据组测试时，均小于该组的误差平均值，可知检测系统的误差与标定面每次检测所转角度的幅度大小有关。

为了解决制孔精度低、设备价格昂贵等一系列存在于飞机自动制孔阶段的问题，本文提出了一种基于多激光传感器安装的法线找正方法。实验发现，导致制孔法向精度较低的原因有：（1）坐标系建立的误差；（2）机械手空间移动误差；（3）激光位移传感器测量误差。本文提出的方法可有效补偿激光位移传感器测量时的安装误差及检测设备在加工过程中所产生的误差。从而有效降低法线找正时的角度偏差值，为实际工作中机器人制孔精度提供了保证。

5 结论

自动钻铆系统以其对飞机自动化装配的高效率，被技术人员所认可[24]。但是激光位移传感器在工作中所产生的装配误差、磕碰、偏移等状况，使加工孔定位准确程度受到严重影响。针对以上问题，本文提出了在自动钻铆系统中，基于多激光传感器安装的自由曲面法线方向检测技术，并建立了该方法的几何模型，及其误差补偿模型。该模型基于自适应标定流程，方法简单且检测精度较高。验证结果显示，标定后检测装置得出的法线方向偏差值均小于0.5°，平均值为0.066 7°，满足自动钻铆系统中对于飞机装配孔垂直精度的要求。

通过进一步分析本次实验结果得知，对于本文所研究的自动制孔系统的定位误差，其影响因素较多。在以后的研究里，若要进一步提高实际系统的法线检测精度，可使用设计精密的基准检测装置，如精密电机和直线导轨做平移及旋转运动，以及采用更高精度的传感器测量等一系列策略。本文提出的补偿算法只能补偿加工时由几何参数所造成的定位误差，虽然可以满足现有的项目工况要求，但是如果有更高的工作环境要求，如温度等，则需要进一步研究误差补偿策略，优化自适应法线找正方案，提高标定算法的可靠性与适应性。