注射成型发泡过程中温度和剪切速率对CO2扩散行为影响的分子动力学研究

蔡恒芳，孙 玲*

（南昌大学机电工程学院，南昌330031）

0 前言

PLA 是一种新型环保型塑料，广泛应用于医学、食品、纺织等领域［1-2］。PLA韧性差，质硬等缺点限制了其代替石油基塑料应用于日常生活中。随着微发泡技术不断成熟，通过泡孔大小结构改善PLA在应用中的缺陷，PLA发泡塑料以其优异的隔热、减震、缓冲、密度低等性能在日常生活中得到广泛应用［3-4］。与传统的采用碳氢化合物等作为发泡剂的泡沫塑料相比，采用小分子CO2或N2作为物理发泡剂，超临界流体（Supercritical Fluids）技术发泡成型的微孔发泡塑料的泡孔更加细腻均匀，发泡工艺更加绿色环保［5］。而气体动力学扩散过程对泡孔显微结构及材料使用过程中性能优良起着决定性作用。因此，CO2在PLA扩散行为影响泡孔形态从而影响其力学性能。分子动力学模拟（MD）是通过一系列模拟运算预测体系内粒子间的相互作用从而估算其物理性质，常采用Einstein 法和Green-Kubo 法两种方法计算扩散系数［6-8］。Wang［9］等基于分子动力学的方法研究了在高温和低温情况下，13 种小分子在聚对笨二甲酸乙二醇（PET）中的扩散行为，研究结果表明MD模拟结果与实验值一致。Dumitru［10］等研究CO2和N2在PET和相关芳香族聚酯共混物中的扩散行为，采用分子动力学模拟分析温度、密度、自由体积等对扩散系数的影响，研究发现扩散系数与自由体积的正相关性。尽管国内外研究者对超临界CO2辅助PLA发泡工艺进行大量实验研究，但是基本都从宏观角度分析，从分子和原子水平揭示微发泡注射成型过程CO2的扩散行为研究很少。分子模拟方法可精确设置工艺参数，采用控制变量法从分子水平揭示温度、压力、自由体积、密度和扩散原子等对扩散的影响。在注射发泡过程中，聚合物流体由于注射速度不同将受到不同程度的剪切作用，本文采用分子动力学方法建立PLA和CO2模型，通过计算粒子的平均平方位移并对其进行微分来计算扩散系数（Einstein 法）。研究高分子链运动与CO2分子在PLA中扩散行为之间的关系，模拟计算CO2在PLA中的扩散系数，从剪切速率和温度2个不同的维度来讨论PLA主链的活跃性、均方回转半径、体系能量对气体扩散的影响。

1 模型构建与模拟方法

注射发泡成型与挤出发泡成型相比，可成型较复杂零件，其工艺流程与传统注射成型相似，在充模过程前在聚合物溶体扩散室形成大量微气泡核。根据“蛇形理论”——P G de Gennes提出的用来描述无规线团分子运动以及“管道模型”——Edwards 提出的用来描述聚合物的缠结分子链运动，因此，聚合物链运动行为可近似视为在由其他分子链组成的管状空间或栅格内的蠕动的过程［11-12］，采用Einstein 模型来计算气体的扩散系数。本文采用Materials Studio 软件构建了PLA/CO2复合体系模型。首先用Visualizer 模块构建CO2分子和聚合度为30 的PLA高分子链。用Amorphous Cell构建体系目标密度为1.24 g/cm3的PLA周期性无定形元胞，元胞参数如表1。为使模拟环境接近宏观实际体系，对无定形元胞进行能量最小化处理，得到合理的几何构象，减少“链端效应”。几何优化过程中力场采用第一个从头算（COMPASS）力场、Smart方法，能量收敛水平为0.000 01 kcal/mol，Andersen 控温，Berendsen 控压。对元胞进行温度从300 K 到500 K的5个循环的退火处理，温度梯度为25 K，时间步长为1 fs。最后为消除体内不合理构象，对元胞进行足够长时间的预平衡处理，在恒温恒容（NVT）下进行1 000 ps的分子动力学驰豫。为研究不同剪切速率和温度下CO2扩散系数变化情况，设定压强恒定为12 MPa，对PLA、CO2混合体系在X-Y平面施加不同恒定的剪切应力，剪切速率分别为0、0.01、0.25、0.5、1 ps-1。考虑温度对气体扩散影响，不同剪切应力作用后的模型分别在358、368、378、388 K 温度下驰豫1 000 ps，整个模拟过程采用恒温恒压（NPT）系综，COMPASS力场，Andersen控温和Berendsen控压，时间步长为0.5 fs。

表1 PLA模型元胞组成Tab.1 Cell components of PLA and composite models

2 结果与讨论

2.1 CO2扩散系数

以CO2为扩散分子，模拟在微发泡注塑保压阶段气体在PLA 基体中的扩散情况。在分子模拟中，通常采用Einstein 方程来计算分子的扩散系数，见式（1）。在计算扩散系数时，式（1）可以简化成式（2）：

图1 PLA/CO2模型Fig.1 Simulation models for PLA/CO2

提取构象在NPT 系综下的运功轨迹，模拟分析可得CO2在不同剪切速率和不同温度下在PLA中的均方位移曲线如图2 所示。图2（a）显示，在未受到剪切力作用时，均方位移-时间（MSD-t）曲线先呈指数增长后趋于线性增长，随着温度升高，MSD 值也逐渐升高，扩散系数增大，模拟结果与晏梦雪［13］、石剑［14］等实验结果相同，说明模拟环境合理。当体系受到不同程度剪切力作用时，随着剪切速率（γ˙）的增大，MSD 值逐渐增大。但受剪切力作用后，MSD 随温度变化规律发生改变，当γ˙＞0.1 ps-1时，体系处于368 K 时CO2扩散能力显著增强，优于其他温度（358、378、388 K）。γ˙=1 ps-1，温度为368 K 时，CO2扩散系数达到17.742 6×10-5cm2/s，比未受剪切作用时CO2扩散系数提高了143.96 %。对分子模拟的MSD-t 曲线线性拟合得到斜率k，带入式（2）可得CO2在PLA 中的扩散系数如图3 所示，具体数值如表2。模拟结果表明CO2在PLA中的扩散系数和温度、剪切速率都密切相关，温度、剪切速率大小影响PLA 分子链和CO2分子的运动状态，从而改变CO2扩散系数。

图2 CO2在不同温度和剪切速率下的均方位移Fig. 2 Mean square displacement of CO2 at different temperature and shear rate

2.2 PLA主链活跃性

高分子链在单键内旋作用下会产生分子在空间的不同构象，如无规线团、伸直链、折叠链等等。高分子链构象不同，柔顺性发生变化，能量也发生变化。MSD可表征聚合物分子链在一段时间内的取向迁移情况，为进一步研究CO2在微发泡注射成型过程的扩散机理以及PLA 分子链运动对CO2扩散的影响，模拟计算不同温度和剪切速率下PLA 分子主链的MSD-t 曲线，如图4 所示。PLA 分子主链段的均方位移图可描述主链的活跃性，观察MSD-t 曲线斜率可初步判断主链的活跃性。图4中显示，剪切速率为零时，温度越高，主链越活跃。对比前面CO2分子的MSD-t 曲线图可知，相同条件下，PLA 分子链的取向迁移和CO2的均方位移变化情况一致。PLA 主链活跃性越大，CO2的扩散系数越大。因为在温度较低情况下，PLA 分子链相当于处于“冻结”状态，只有小部分链段和端基小范围运动，体系内扩散通道较少，气体迁移扩散困难。随着温度逐渐增高，体系能量不断增大，PLA 分子链段被激活，CO2分子拥有更高的能量使其越过能量势垒，扩散通道增多，气体的扩散系数增大，与晏梦雪等［13］实验研究结果一致。同温度下，剪切速率越大，主链越活跃。根据描述高分子本体微尺度形态演化的De Gennes［15］模型和描述具有缠结本体的Doi-Edwards［16］模型，在微发泡注射成型过程中PLA 受到剪切应力作用时，克服体系内分子间的作用力、扭结力以及周围大分子链阻碍，受一定程度的剪切应力作用时，分子链解开缠结约束并沿剪切方向产生定向排列和迁移，体系内部存在一个“活化能”［17］。当剪切速率为0.1 ps-1时，“活化能”存在阻碍了分子链形态变化，而当剪切速率增大到0.25 ps-1时，挣脱了这种“活化能”的束缚，原子迁移效应变明显，分子链产生新的构象。分子链越活跃，为气体扩散提供扩散通道，气体扩散系数增大。为验证该理论，应对进一步研究体系内能变化情况。

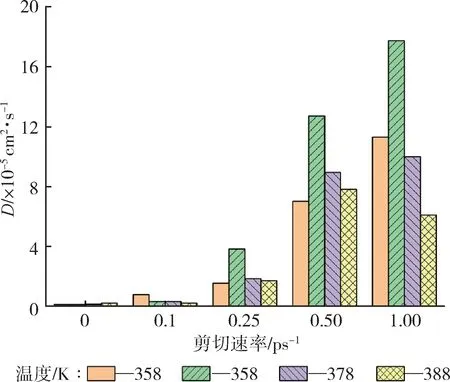
图3 CO2在不同温度和剪切速率时的扩散系数Fig.3 Diffusion coefficient of CO2 at different temperature and shear rate

表2 不同温度和剪切速率下CO2在PLA中的扩散系数10-5 cm2/sTab.2 Diffusion coefficient of CO2 at different temperature and shear rate 10-5 cm2/s

图4 PLA主链在不同温度和剪切速率下的均方位移Fig.4 Mean square displacement of the main chain of PLA at different temperature and shear rate

2.3 体系能量响应

为进一步研究验证CO2在PLA 中的扩散机理，分别模拟计算了不同剪切速率和温度下体系的总能量响应图，如图5 所示。由于γ˙为0.1 ps-1时，剪切速率对CO2扩散影响较小且作用规律相同，篇幅原因不赘述。所有体系随着时间的推移体系总能量逐渐稳定在某一个数值，当剪切速率相同时，体系总能量随着温度的升高逐渐升高。这验证前面体系能量越高，聚合物分子链越活跃，CO2分子能量越高越容易挣脱束缚，扩散系数越大。受剪切作用体系，在剪切力的作用下分子链解开缠结挣脱束缚，体系能量大幅提高且剪切速率越大，能量越高。在恒温恒压阶段前期（0～50 ps），体系能量较高出现能量峰值，γ˙为0.25、0.5、1 ps-1，能量峰值与未受剪切力作用体系相比分别提高32.69 %、53.85 %、198 %。CO2分子和PLA 主链段越活跃，扩散速度较快。

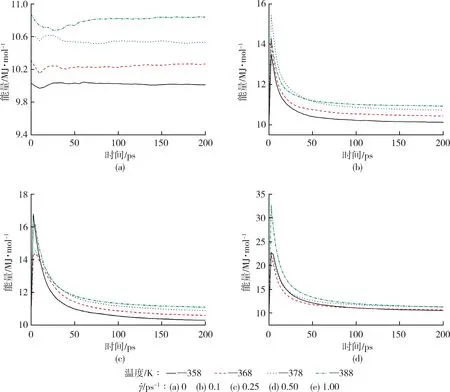
图5 不同温度和剪切速率下体系的总能量Fig.5 Total energy of the system at different temperature and shear rate

2.4 回转半径

聚合物分子链由于内旋转作用会形成不同的空间构象即分子链的柔顺性，同时分子链还具有多样。因此，为进一步了解PLA分子链运动形态对CO2扩散系数的影响，计算模拟PLA 主链在不同温度和剪切速率下的回转半径（Radius of gyration）响应曲线，见图6。在实验中测量聚合物链的回转半径通常采用光散射法，回转半径表征聚合物分子链单体原子到质心的距离，可直观反映分子链的尺寸和空间分布，公式如式（3）所示：

式中 Rg——分子链回转半径

Mi——第i个原子质量

si——第i个原子到质心的距离

n——分子链单体原子数目

由图6可知，从回转半径峰值分布情况来看，温度对PLA主链回转半径影响较小，在相同剪切速率下，PLA主链回转半径峰值分布基本相同，这可能有由于温度梯度不够大，差异不明显。剪切应力越大，峰值分布越分散且逐渐右移。这说明剪切速率较小时，PLA主链在质心位置附近有更大的分布概率。从回转半径径向分布情况来看，随着剪切速率的不断增大，回转半径的分布范围也逐渐变大，分布范围从γ=0 ps-1时的12.91×10-10～21.75×10-10m，增大到γ=0.25 ps-1时13.73×10-10～32.93×10-10m，γ=0.5 ps-1时14.14×10-10～36.95×10-10m，γ=1 ps-1时最后区间增大到13.42×10-10～36.98×10-10m。该情况说明剪切速率越小，PLA主链原子分布越密集；随着剪切应力增大，主链原子分布趋于分散，主链沿剪切方向发生取向变形。微观上表现为未受到剪切力作用时，PLA分子链呈缠结卷曲状态，随着剪切速率增大，分子链解开缠结，沿剪切方向定向排布，回转半径分布范围变大，模拟结果与曹文化等［17］研究结果相符。PLA主链解开缠结，挣脱束缚，分子链能量越高，运动越活跃，从而促进CO2在PLA中的扩散。

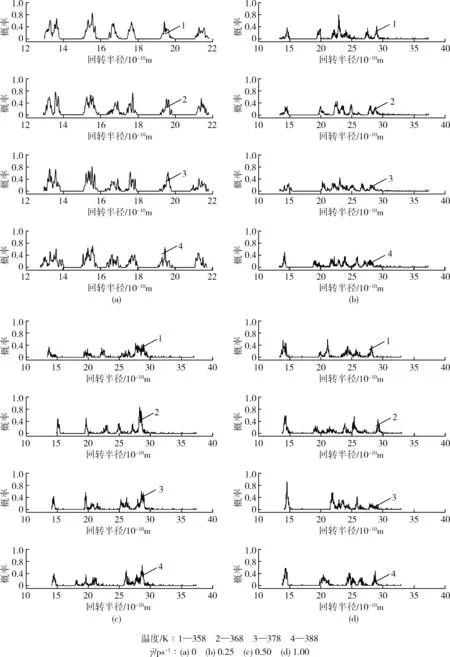
图6 不同温度和剪切速率下PLA主链回转半径的响应曲线Fig.6 Radius of gyration response curves of the main chain of PLA at different temperature and shear rate

3 结论

（1）建立PLA/CO2体系，采用分子动力学模拟方法模拟超临界CO2辅助PLA 微发泡注射成型过程中，体系受到不同的温度和剪切速率作用，模拟计算CO2气体分子的均方位移，PLA 分子链的均方位移、均方回转半径、体系能量等参数，分析对比得到温度和剪切速率对CO2扩散行为的影响；

（2）PLA/CO2体系未经剪切应力作用时，CO2扩散系数与温度呈正相关。在低温情况下，PLA 分子链处于冻结状态，高分子链段能量较小，分子链活跃性较低，体系内“扩散通道”较少，CO2扩散系数越小；温度逐渐升高，高分子链能量不断增大，达到跃迁能量势垒，分子链逐渐挣脱束缚，CO2扩散系数逐渐增大，在温度为358 K 时，CO2扩散系数为0.118 2×10-5cm2/s，温度升至388 K时，达到0.219 8×10-5cm2/s；

（3）体系受到剪切应力作用后，CO2扩散系数剪切速率呈正相关；PLA 分子链受到剪切力的作用，分子链之间的缠结网络逐渐被破坏，分子链脱离缠结产生流动取向，方向和剪切方向一致，剪切速率越大分子链的迁移范围越大，分子链能量越高，运动越活跃；温度对CO2扩散系数影响规律变化，在温度为368 K 时CO2扩散能力显著增强，扩散系数大于其他温度（358、378、388 K）。