基于 Nurbs 曲面引入 Kriging 近似模型对壳体结构进行拓扑优化

谈凤婕

（华东建筑设计研究院有限公司，上海 200011）

0 引言

在空间曲面壳体结构的设计中，合理的曲面可以提高结构空间传力性能。对于复杂的曲面结构，普通的方程不能简单有效地表达曲面，可能需要多段曲线方程来拟合曲面壳体结构，同时增加优化变量的数量，增加优化的计算量，降低优化效率。利用 Nurbs 曲面，可以通过调整曲面上的控制点来改变曲面形状，不仅可以灵活拟合曲面，而且可以控制优化变量，提高优化效率。

国内外学者在利用 Nurbs 进行建模分析的方面展开了多项研究。文献［1］利用 Nurbs 对球艏构型进行拓扑优化；文献［2］利用 Nurbs 对叶轮进行建模分析；文献［3］利用 Nurbs 对汽车壳体进行模拟建模；文献［4］基于 Nurbs提出 TOP-IGA-MMV 方法。

在结构的拓扑优化中，当设计变量的个数变多时，往往需要更多的迭代步骤以找到全局最优解，然而在结构分析中，当结构形式复杂，单元划分数量大时，有限元分析本身就非常耗费时间，再加上优化分析的迭代数量，使得优化过程计算效率十分低下。为了解决计算效率的问题，引入 Kriging metamodel 来近似模拟真实模型，从而简化计算过程。

国内外有大量对近似模型的研究和应用。文献［5-6］证明了 Kriging metamodel 可以提供一个很好的近似模型来模拟真实模型；文献［7］对比了多种近似模型应用于考虑不确定因素时的优化问题，发现 Kriging metamodel的精度最好。

本文利用 Nu r b s 对壳体建模，生成网格，利用 Ansys 进行有限元分析，通过调整控制点的位置改变壳体形状，利用遗传算法找寻控制点最优位置，以壳体的应变能最小作为目标函数，引入近似模型简化优化分析过程，寻找最优化的壳体曲面形状。

1 Nurbs 曲面

Nurbs 是 B-spline 通过等参转换得到。B-spline 的基本方程有很多构成方法，目前最常用的是由 Piegl 和Tiller 提出的 Cox-de Boor recursion 方程，假设｛ui｝（i=0，2，3，…，m）是一系列非减结点（ui≤ui+1）中的第 i 个结点，则在半开区间［ui，ui+1）上的 p 阶基本方程如式（1）所示。

式中：n，m，p 满足 m=n+p+1。

然而 B-spline 不能灵活有效地表达一个圆，因此通过等参转换，得到 Nurbs（见图 1），则 p 阶Nurbs 曲线表达式如式（3）所示。

式中：wi是和控制点Pi相关的权系数。将曲线扩展到曲面，得到 Nurbs 曲面的表达式如式（4）所示。

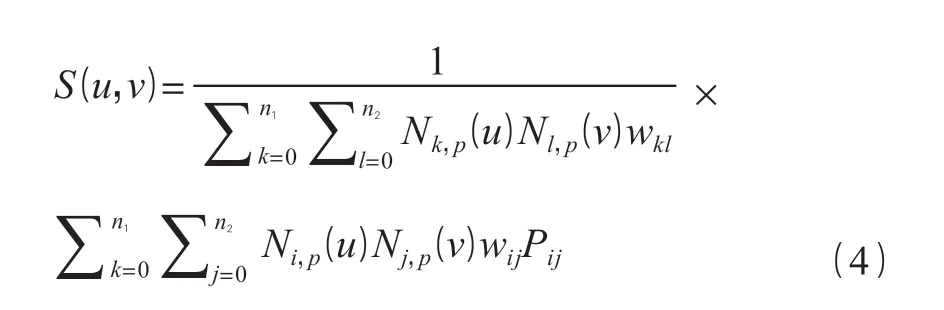
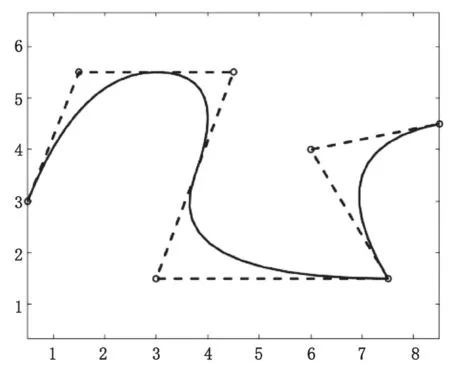
图1 Nurbs 曲线

2 壳体结构拓扑优化实例

当需要建立一个比较复杂的几何形状时，通过分析方程去建立该几何形状，会导致曲线分段过多，分析方程太复杂，计算不方便等问题，然而通过移动控制点来得到想要的几何形状是一种比较灵活有效的方式。

本文案例为一个蝴蝶形空间大跨壳体结构，x 向跨度 280 m，y 向跨度 115 m，底部支撑由剪力墙和摇摆柱组成。本文只探讨结构形状的优化，只从结构形状建模的角度出发。选取壳上 12 个控制点建立结构的几何形状，如图 2 所示。

2.1 优化方程

本文的目的是通过移动建模时使用的 12 个控制点，来调整壳体各个位置的矢高，从而产生拱效应，减小结构产生的应变能。因此选取 12 个控制点的竖向坐标作为设计变量，控制点的竖向坐标变化范围为［2，20］，最小总应变能为优化目标，则其相应的优化方程如式（5）所示。

图2 初始模型

式中：x 是设计变量；f（x）是目标方程；lb 是设计变量取值上边界；ub 是设计变量取值下边界。

2.2 优化方法

本文使用的优化算法是遗传算法［8］，遗传算法是一种全局优化方法，其在指定的搜索区域内，通过模仿遗传学特性，将设计变量编码后看作“染色体”，例如利用二进制编码，将染色体组合交叉和变异逐代演化出更好的近似解，从而得到全局最优解。遗传算法流程图如图 3 所示。

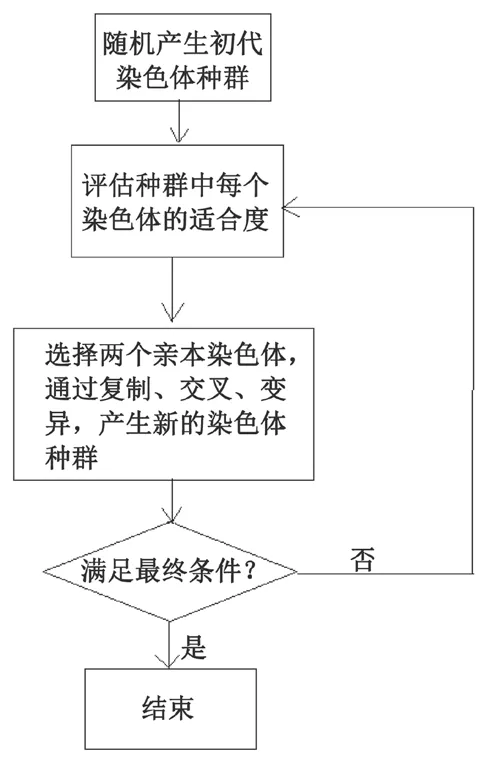
图3 遗传算法流程图

利用遗传算法对上述壳体进行优化，优化后得到的结构形状如图 4 所示，得到结构的应变能分布如图 5 所示。

3 利用近似模型进行优化

图4 优化模型

图5 应变能分布（单位：kJ）

在结构的拓扑优化中，当设计变量的个数变多时，往往需要更多的迭代步骤以找到全局最优解，然而在结构分析中，当结构形式复杂，单元划分数量大时，有限元分析本身就非常耗费时间，再加上优化分析的迭代数量，使得优化过程计算效率十分低下，因此，需要引入新的方法来提高计算效率。考虑利用近似模型，建立设计变量和优化目标之间的关系，可以减小优化分析时对结构进行有限元分析的次数，从而提高优化效率，减少计算时间。

Kriging 是一种依据协方差函数［9］，根据已知数据建立一个空间模型来进行预测的回归算法。在特定的随机过程中，Kriging 可以给出最佳的线性无偏估计。假设建模对象遵循高斯随机过程，则得到相应的 Kriging metamodel 如式（6）所示。

式中： βTf（x）是这个高斯随机过程的平均值，βTf（x）=β1f1+β2f2+…+βPfP）；Z［x，R（x，x′；θ）］是一个均值为零的高斯随机过程；σ2是该高斯随机过程的方差；R（x，x′；θ）是观测点与预测点之间的相关函数；θ是模拟空间的相关长度。

Kriging metamodel 的计算原理为通过已知的设计点 X={x1，x2，x3，…，xN}T和相应的输出值 y={y1，y2，y3，…，yN}T来预测在点 x 处的Y＾=μk（x），根据式（6）可知，设计点和预测点服从高斯联合分布，如式（7）所示。

式中：Fij=fj（xi）（j=1，2，…，P；i=1，2，…，N）；R 为已知值与预测值之间的相关函数（见图 6）；θ 为相关长度。常用的相关函数有线性相关函数、指数相关函数、高斯相关函数、Markov 相关函数。

图6 相关函数（其中 θ=1，τ=x-x′=1）

利用 Kriging metamodel 建立模型的设计变量和目标方程的近似模型，其中相关函数为指数相关函数。随机生成 50 个样本，得到真实模型和近似模型间的对比，如图 7 所示。

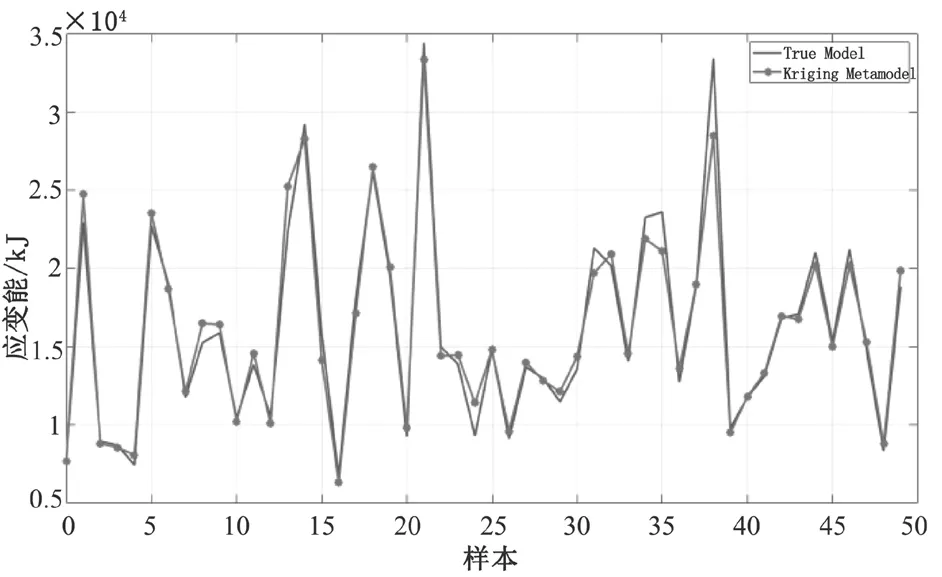
图7 真实模型和近似模型之间的对比

利用近似模型来对设计变量进行优化，得到优化模型如图 8 所示，近似模型优化结果和真实模型优化结果对比如表 1 所示。

图8 优化模型

图9 应变能分布（单位：kJ）

表1 真实模型优化结果和近似模型优化结果对比

由表 1 可以看出，由近似模型计算通过有限元法所得到的优化结构的应变能为 4.386×103kJ，由有限元法计算的通过真实模型得到的优化结构的应变能为 4.066×103kJ，由近似模型计算通过近似模型得到的优化结构的应变能为 3.956×103kJ，由有限元法计算通过近似模型得到的优化结构的应变能为 4.386×103kJ。近似模型能够预判设计变量和优化目标间的关系，由近似模型得到的优化结果接近真实模型的优化结果，然而由于近似模型存在误差，使得由近似模型得到优化结果并不是真实的最优结果。

4 结论

本文利用 Nurbs 曲面建模，将控制点坐标作为设计变量，通过调整控制点坐标，利用遗传算法优化结构形状，避免了通过分析方程去建立几何形状时遇到的曲线分段过多、分析方程太复杂、计算不方便等问题。

近似模型的应用可以大幅地减少计算时间，简化分析过程，提高优化效率。近似模型和真实模型的计算结果对比，近似模型能够很好地预测设计变量和优化目标的关系。但是，近似模型和真实值之间仍然存在比较明显的误差，这会导致所得到结果接近最优解，但不是最优解。

整体来看，近似模型在结构优化中的应用是一种非常有前景的方法，但是仍需要通过引入一些措施，比如神经网络算法、贝叶斯定理等，来提高近似模型的精确度，减小误差，使得近似模型可以更好地模拟真实结构模型。Q