基于隐半马尔科夫退化模型的非等周期预防性维修优化

苏 春 李 乐

(1东南大学机械工程学院， 南京211189)(2湖南科技大学机械设备健康维护湖南省重点实验室， 湘潭 411201)

长寿命产品的可靠性评估面临故障数据匮乏等难题.近年来，从性能退化的视角评估产品可靠性受到关注.总体上，性能退化建模方法可分为3类，即失效物理方法、概率物理方法和统计模型方法[1].统计模型方法利用全寿命周期的先验知识，实现产品剩余寿命和健康状态预测[2].马尔科夫过程(Markov process)具有无后效性或无记忆性，得到广泛的研究与应用.其中，隐马尔科夫模型(hidden Markov model，HMM)是一类用于描述具有隐含未知参数的马尔科夫过程，根据可观察参数确定过程中的隐含参数；隐半马尔科夫模型(hidden semi-Markov model，HSMM)是HMM的一种扩展形式，它在HMM结构上增加时间因素，能够描述系统状态与外在观测值的内在关系.通过观测值预测系统健康状态的变化趋势，为维修决策提供理论依据.

吴军等[3]采用HMM描述装备运行过程，结合切普曼-柯尔莫哥洛夫微分方程推断装备运行可靠性.Jiang等[4]采用HMM动态预警在役电力变压器的亚健康状态，并验证早期故障预测的有效性.Dong等[5]采用HSMM建立液压泵故障诊断和寿命预测模型，并得出HSMM比HMM能更好地识别故障状态的结论.文献[6]在HSMM基础上，采用多隐半马尔科夫模型(multi-HSMM)预测UN-60A黑鹰直升机传动装置故障与寿命.Liu等[7]采用HSMM完成刀具磨损退化过程建模，描述相邻退化状态持续时间的依赖关系.Li等[8]提出基于隐马尔科夫模型的性能退化建模方法，得到风力机部件的性能退化规律，并完成可靠性评估.Liu等[9]提出切换隐半马尔科夫模型，以描述时变工作模式下的退化过程.

目前，HSMM多用于系统状态评估和寿命预测，而针对运行和维修决策的研究工作较为少见.总体上，维修策略包括事后维修(corrective maintenance)、预防性维修(preventive maintenance，PM)、预测性维修(predictive maintenance)等类型.PM又可分为基于时间的维修和基于状态的维修[10].Chen等[11]采用具有自相关观测值的隐马尔科夫模型预测剩余寿命，并根据剩余寿命提出相应的维修策略.苏春等[12]将退化过程离散成有限个退化状态，以长期折扣成本最低为目标，基于半马尔科夫决策过程建立风力机齿轮箱维修成本模型.陈一梅等[13]以系统年平均总费用最小为目标，建立人字门船闸系统维修周期优化模型，优化成组维修费用.苏春等[14]考虑有效年龄和役龄改善因子，建立可用度约束下的风力机单部件顺序维修优化模型.Chen等[15]针对连续监测下的退化系统，考虑不完全维修提出一种新的CBM优化问题，并采用最优预防性维修阈值实现维修成本和可用性的平衡.Lee等[16]以条件可靠性阈值为约束，建立维修优化模型，实现单位时间内的预期总维修成本最小化.

本文基于监测数据研究设备维修决策优化问题，以去噪后的监测数据作为退化特征观测值，利用HSMM状态退化模型完成数据的训练学习.在退化状态转移过程基础上，结合有效役龄建立非等周期预防性维修优化模型.采用增强精英保留的遗传算法(strengthen elitist genetic algorithm，SEGA)求解模型，得到单位时间费用成本率最小化的预防性维修策略，并通过案例验证方法的有效性.

1 基于隐半马尔科夫的性能退化建模

目前，风力机、工程机械、航空发动机等工程装备中已安装多种类型传感器，可以实时获取监测数据.采用HSMM，通过对观测数据的训练学习可获取装备健康状态、预测性能退化趋势.

1.1 隐半马尔科夫理论

HSMM是一个双重随机过程，其中包括2条链[4]：一条链为马尔科夫链，用于描述状态之间的转移过程；另一条链用于描述状态和观察序列之间的对应关系，但不具备马尔科夫性.马尔科夫特性用于描述系统状态之间的内在关系，具有无后效性，即系统将来的状态仅与当前状态有关、与过去状态无关.对观察者来说，观察值的变化未能充分反映状态迁移过程，HSMM能够通过观察序列来感知状态变化和状态的转移过程.

完整的HSMM可以定义为λ= (π，A，B，D)[5-6]：

1) 状态集H= {hi|i= 1,2,…,I}.其中，hi表示HSMM中第i个隐藏状态，I为状态的数目.

2) 初始状态概率分布π= {πi|i=1,2,…,I}用于描述初始时刻下系统的宏观健康状态，其中πi表示初始时刻第i个隐藏状态出现的概率大小.

3) 状态转移矩阵A={aij|1 ≤i,j≤I}I×I.其中，aij表示系统工作过程中由状态i转移到状态j的概率，也就是当前时刻t的状态st为hi隐状态，而t+1时刻状态st+1为hj隐状态的概率，即aij=P(st+1=hj|st=hi).i、j表示系统所处的不同状态.

4) 状态观测概率矩阵B= {bim|1 ≤i≤I, 1 ≤m≤M}I×M.其中，M为观测变量的数目，t时刻的状态st为hi.此时，第m个观测变量om出现的概率bim=P(om|st=hi)，表示在不同状态下观测值的分布情况.

5) 状态持续时间矩阵D={Pi(d)}.其中，Pi(d)表示状态i出现时间持续d个观测时间的概率，即系统在某个状态下的持续时间.

对于HSMM建模，需要解决评价、解码和训练等3类问题.评价问题是在已知模型λ= (π，A，B，D)下，计算时间跨度为T的某观测序列O={ot|1≤t≤T}的发生概率P(O|λ).解码问题是在已知某观测序列O={ot| 1 ≤t≤T}及模型λ= (π，A，B，D)下，选择最有可能的状态序列H′ = {h′t| 1 ≤t≤T}，使得P(H′|O)最大.其中某时刻t下对应的隐状态h′t是隐状态集合中的某一状态，可采用Viterbi算法.训练问题是通过已知某观测序列O= {o1，o2，o3，…，oT}，估计模型λ= (π，A，B，D)，使得P(O|λ)最大.需要指出，当对退化的监测数据观测值进行HSMM训练时，应保证HSMM的稳定性.

综上所述，基于监测数据观测值的多状态退化模型训练流程如下：

①输入观测值序列O= {o1，o2，…，oT}.

②初始化模型λ= (π，A，B，D)、状态观测概率矩阵B和状态持续时间矩阵D.

③采用Baum-Welch算法调整模型并得到模型λ′.

④对重估模型λ′，采用Viterbi算法计算P(H′ |O).

⑤若P(H′|O)已收敛跳转至步骤⑥；否则，转至步骤④.

⑥输出模型λ′.

1.2 时变状态转移的多状态退化模型

通过引入状态持续时间矩阵，HSMM改进了HMM中无法反映状态持续时间的问题，使之可用于评估系统状态、预测剩余寿命.HSMM存在多种拓扑结构类型，其中左右型拓扑结构适合于描述系统的退化过程，如图1所示.

在左右型拓扑结构中，只能够由前一个状态转移至后续状态，而不能由后续状态跳转至前边的状态；系统的退化过程也是如此，即系统在没有维护时只能由健康状态转变为不健康的状态.通常，系统的退化过程共有I(I≥ 3)个隐变量状态，并以hi(1 ≤i≤I)表示.例如：将系统退化过程分为良好、一般、劣化、故障等4个阶段，即I= 4.系统由状态hi转变为状态hj的概率为aij(1 ≤i,j≤I).同时，HSMM中的宏观状态Hi会产生一个持续时间为di的片段观测值，该片段含有di个微观变量hq来生成对应的观测值oq，下标q为状态的持续时间跨度.

利用HSMM训练退化特征数据，能够得到状态转移矩阵A，并建立系统退化模型.设在状态集H下，已知初始状态概率分布π和状态转移矩阵A，由初始时刻开始，t时刻的状态分布ps(t)及期望状态s(t)分别为

ps(0)=π，s(0)=ps(0)H=πH
ps(1)=ps(0)A=πΑ，s(1)=ps(1)H=πAH
⋮
ps(t)=ps(t-1)A=πAt，s(t)=ps(t)H=πAtH

(1)

由式(1)可知，t时刻A(t) = {aij(t)} =At(t= 0，1，2，…).状态转移矩阵A是一个固定矩阵，该方法只能计算离散时间点下的状态转移矩阵.

为计算连续时间下t时刻的状态转移矩阵A′(t)，可采用适应函数fij(t)对{aij(0)，aij(1)，…，aij(t)，…}进行拟合.当t属于(r-1,r)区间(r=1，2，…)时，采用插值法可求得连续时间下的a′ij(t)，以及时变状态概率转移矩阵A′(t) = {a′ij(t)}.其中a′ij(t)可表示为

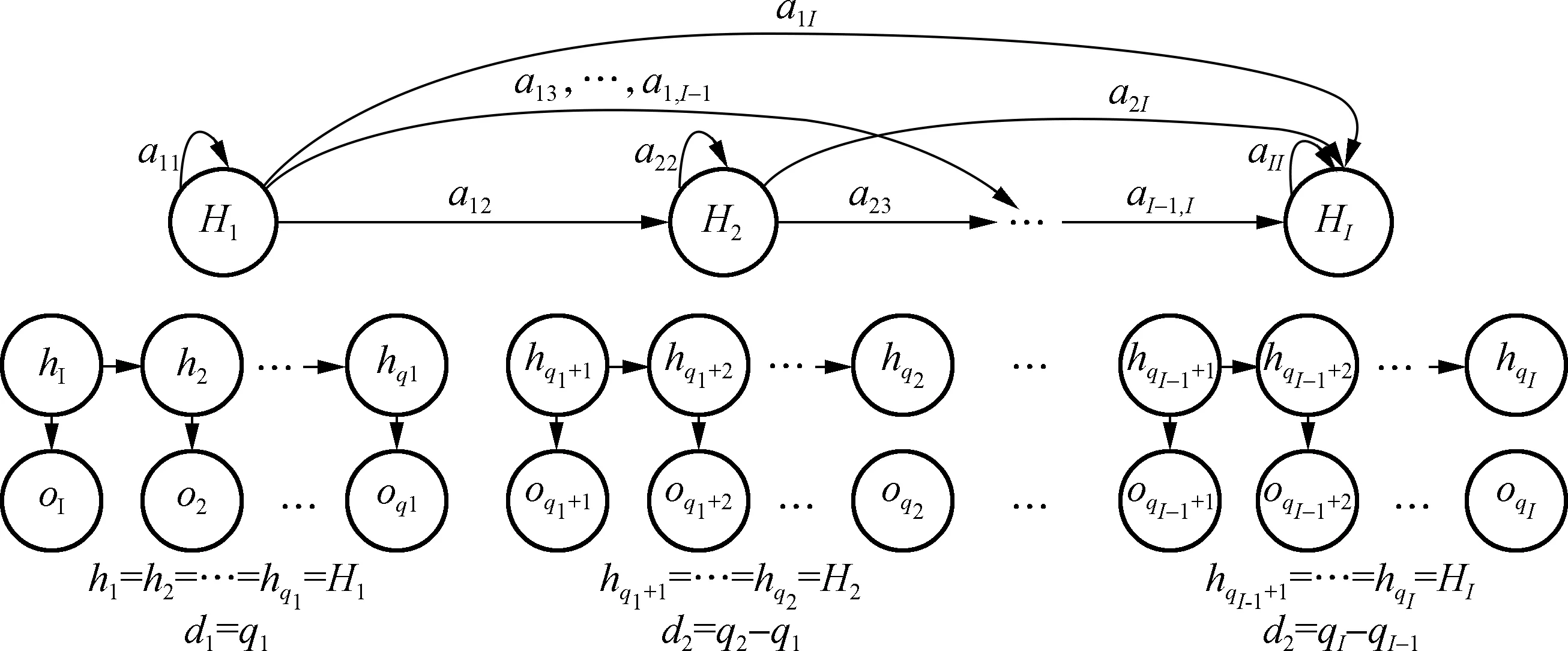
图1 左右型HSMM

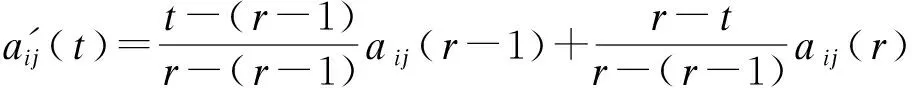
(2)

通过插值法逐个得到a′ij(t)后，时变状态概率转移矩阵A′(t)为

(3)

因此，t时刻下状态分布ps(t)及期望状态s(t)分别如下：

ps(t) =πA′(t)

(4)

s(t)=ps(t)H=πA′(t)H

(5)

HSMM通过对全寿命周期下监测数据的训练学习，能够以时变状态概率转移矩阵A′(t)描述健康状态间的变化关系.对于某个具体系统，在初始状态概率分布π的基础上，可由式(4)、式(5)描述系统随时间变化的退化过程.

2 基于多退化状态的预防性维修模型

系统运行过程通常伴随着维修活动.此外，在系统退化过程中通过采用合适的预防性维修措施可以改善系统健康状态，延长设备寿命.

2.1 非等周期预防性维修模型

图2所示为设备预防性维修过程.其中，L为设备全寿命周期；Tk为第k个预防性维修周期，1 ≤k≤K；K为不同长度的维修间隔期数目；tk为第k(k=1，2，…，K)次预防性维修的时刻.系统在tK时刻进行预防性维修后，当系统不能恢复正常工作状态时，则进行更换，标志着系统生命周期结束.因此，系统全寿命周期可表示为

(6)

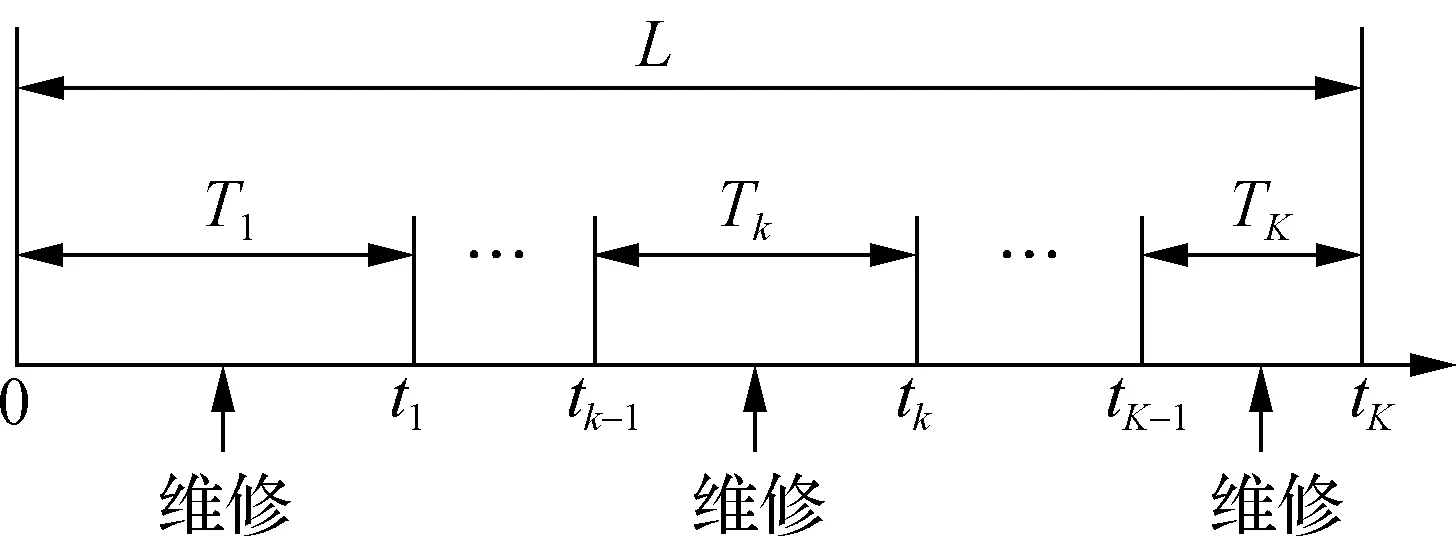
图2 预防性维修过程

随着系统运行时间的增长，状态转移矩阵A′(t)会导致系统状态越来越易于转移至非健康状态，因此预防性维修周期是逐渐缩短的，即T1>T2> …>Tk> … >TK.假设非等周期下的相邻维修周期存在一定比例αk(0 <αk< 1，1 ≤k≤K-1)，即T2=α1T1，T3=α2T2,…，TK=αK-1TK-1，则第k个预防性维修周期为

Tk=α1α2…αk-1T1k=1，2，…，K

(7)

考虑到系统随运行时间和维修次数的增加，其有效役龄将会减少，引入维修改善因子α(0 <α< 1)表示系统状态改善效果.

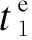
(8)

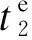
(9)

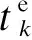
(10)

维修间隔的时间序列{T1，T2=α1T1，…，TK=αK-1TK-1}为递减序列，第k次维修的恢复效果αTk-1也会随着时间减小；维修后的恢复效果越差，维修周期越短.因此，可将α1，α2，…，αK-1等同于改善因子α，即α1=α2= … =αk-1=α,则第k个预防性维修周期Tk以及系统全寿命周期L可以分别表示为

Tk=αk-1T1

(11)

(12)

(13)

由式(5)，若采取预防性维修，在tk时刻系统期望状态为

(14)

假设在全寿命周期L内系统均能正常工作，在任意时刻tk的期望状态应大于正常工作的状态阈值(εs)，即

s(tk)≥εsk=1,2,…,K

(15)

2.2 维修成本模型

预防性维修成本主要包括维修周期内的最小维修总成本(C0)和预防性维修总成本(CK).由于维修周期内发生的故障为非预期故障，系统在维修周期内转换至最后一个状态时，需完成最小维修以确保正常运行，设每次最小维修的成本为c0.因此，在第k个维修周期内的任意时刻tk，发生故障而采取最小维修的概率为p0(tk) =P[stk=hI|tk]，可进一步表示为p0(tk)=ps(tk)[0, 0, …, 1]T=πA′(tk)[0, 0, …, 1]T.因此，系统在K个维修周期内最小维修的总成本可表示为

(16)

设每次预防性维修成本为固定值c，则在全寿命周期内系统维修总成本C可表示为

(17)

2.3 维修优化模型

以维修总次数K、初始维修周期T1为决策变量，以每个作业周期费用率Cr最小化作为预防性维修的优化目标，Cr=C/L.联立式(12)、(16)和(17)可知，Cr是以K、T1、c0和c为变量的函数，可表示为Cr=C/L=g(K,T1;c0,c).因此，维修优化模型可表示为

(18)

联立式(11)、(15)、(17)和(18)，可确定单次最小维修成本c0和单次预防性维修成本c.此外，K和T1需满足K个不等式，以保证系统的期望状态始终不低于正常工作的状态阈值.

可采用SEGA算法求解上述优化模型.SEGA算法能够避免遗传算法中最优个体因选择、交叉和变异操作被破坏的问题.精英个体是种群进化到遗传算法迭代过程中搜索到的适应度值最高的个体，具有良好的基因结构和寻优特性.精英保留策略能有效改进并保留标准遗传算法的全局收敛能力[17].SEGA算法的基本步骤如下：

①初始化种群.

②计算个体适应度函数值.

③基于适应度数值对个体进行排序.

④从个体中选择母体.

⑤交叉母体.

⑥对交叉后的母体进行变异.

⑦合并母体和父代种群产生新的种群.

⑧判断新种群是否收敛.若未收敛则跳转至步骤②，否则结束并输出结果.

3 案例分析

本文采用PHM08数据集作为全寿命监测数据[18].该数据包含218个航空发动机的全寿命数据，每个发动机分别有21个传感器数据，其物理含义分别为：风机入口总温度、低压压缩机出口总温度、高压压缩机出口总温度、低压汽轮机出口总温度、风机入口压力、旁路管道内的总压力、高压压缩机出口总压力、物理风扇转速、物理核心转速、发动机压力比、高压压缩机出口静压、燃料流量与高压压缩机出口静压比率、修正风扇转速、修正核心转速、旁路比、燃烧器燃料空气比、流量焓、需求风扇转速、修正需求风扇转速、高压涡轮冷却剂排放量、低压汽轮机冷却剂排放量.

上述21个传感器对每个发动机由开始工作监测至故障失效.每个发动机的制造误差和初始磨损不同，因此监测数据的时间长度不完全相同.由于传感器数据中含有噪声，因而采用经验模态分解(empirical mode decomposition，EMD)方法将传感器采集的数据分解为若干个分量，将高频分量作为噪声并剔除，将低频部分合成为去噪后的数据[19].如图3所示，以第1个发动机风机入口的总温度数据为例，原始数据模式复杂，噪声造成数据不够平滑.如图4所示，利用EMD算法将该数据分解为6个子信号，其中子信号5和子信号6在数值0附近波动且无规律，为噪声信号.最终，合成子信号1、2、3和4得到去噪后的数据，去噪数据变得平滑并具有一定的规律性，如图5所示.

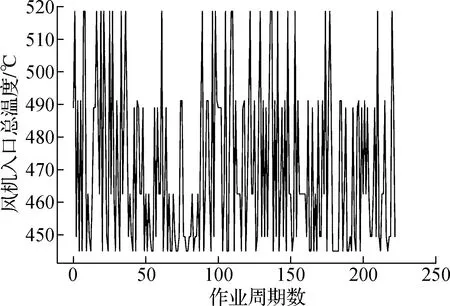
图3 风机入口总温度的原始数据

案例中的观测值有21个维度，训练HSMM时可以采用多维高斯分布函数描述状态观测概率矩阵B.将发动机退化过程分为良好、一般、劣化、完全故障等4个阶段，得到状态集H={0，1，2，3}，其中0、1、2、3分别表示完全故障、劣化、一般、良好.针对HSMM采用改进的Baum-Welch算法完成训练学习，似然概率P(O|λ)的对数值反映了模型通过隐含变量对观测值的拟合程度，即模型的学习效果.随着迭代次数的增加，似然概率对数值也随之增加，但超过一定迭代次数后似然概率对数值不再变化，表示模型已收敛.图6为本例HSMM的训练过程.

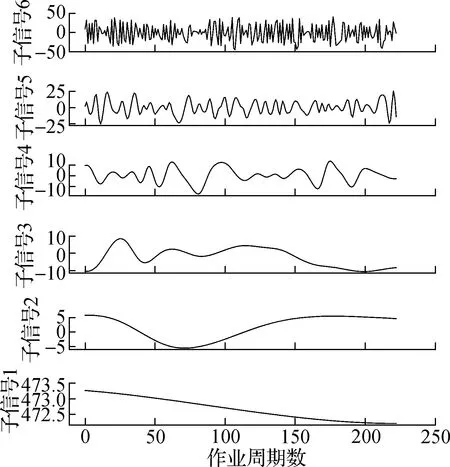
图4 采用EMD算法分解后的风机入口总温度数据

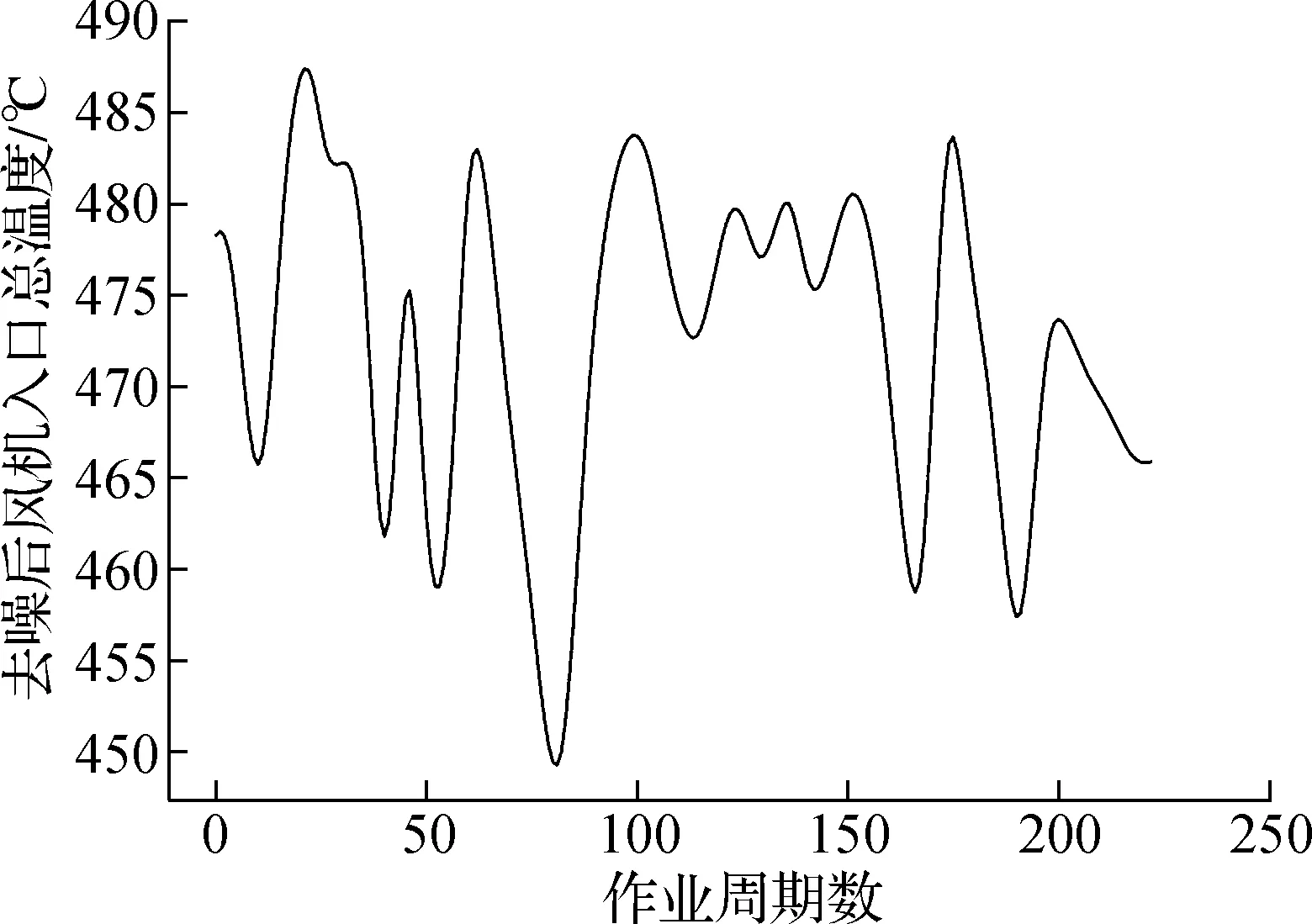
图5 风机入口总温度去噪后数据

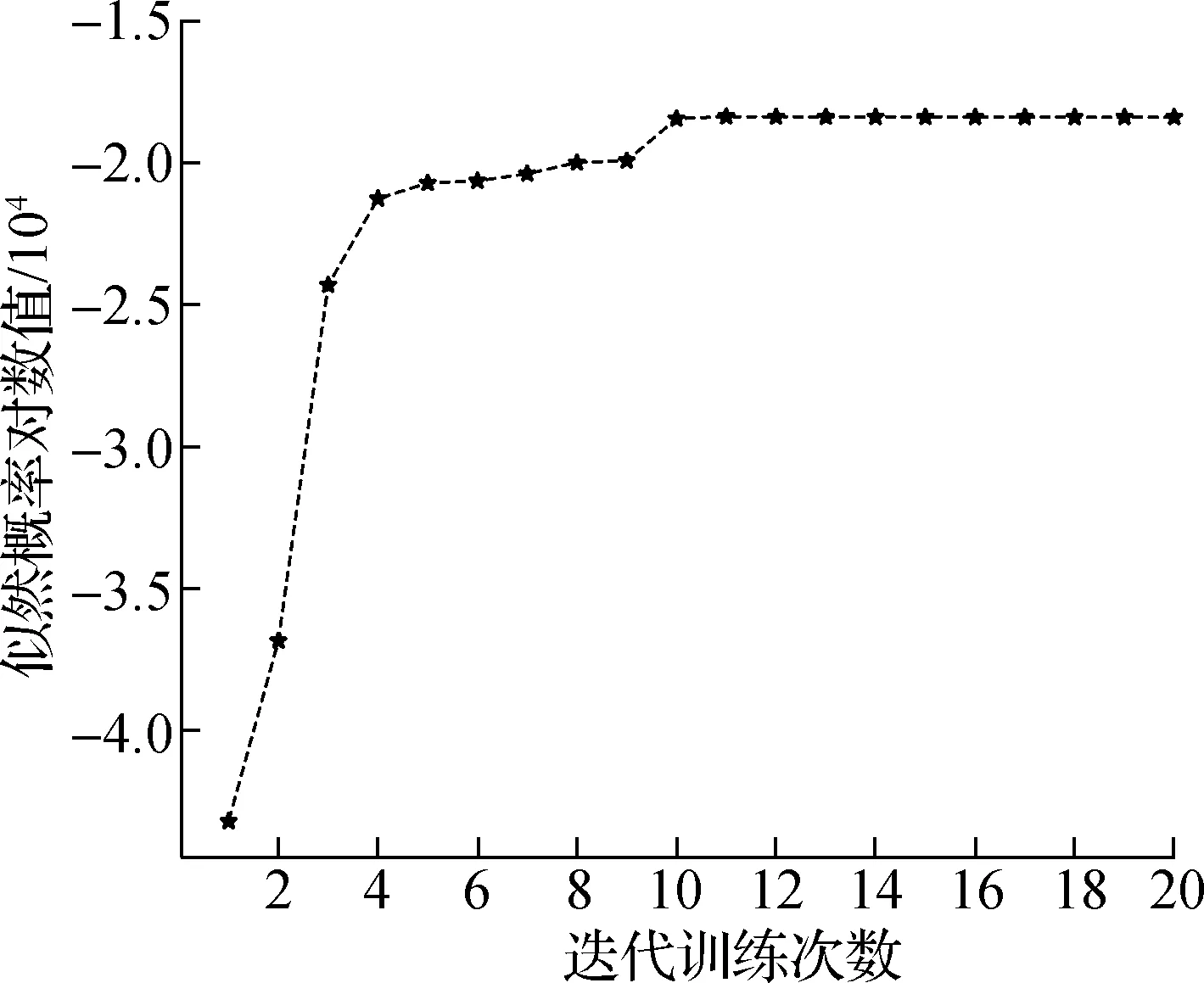
图6 HSMM似然概率对数值迭代过程

本案例中，HSMM在20次迭代训练后收敛，即模型训练完成，状态转移矩阵A为

基于状态转移矩阵A(t) =At(1 ≤t≤T)求得时刻t下离散点aij(t)，由式(2)、(3)、(13)求得有效役龄下的时变状态概率转移矩阵A′(te).由于采用左右型HSMM描述退化过程，因此a21(te)、a31(te)、a32(te)、a32(te)、a41(te)、a42(te)、a43(te)均为0，即系统不能自己由差状态转移至好状态；同时a44(te)=1，即系统一旦到达完全故障状态，将停留在该状态.此外，图7描述了其余aij(te)的时变趋势.a11(te)、a22(te)、a33(te)的数值逐步减小，表明随着有效役龄增加，系统先后越来越难以停驻在良好、一般及劣化状态；a12(te)、a13(te)、a23(te)的数值先增大后减小，即系统越来越容易地由良好状态转移至一般、劣化状态，再由一般状态转移至劣化状态；a14(te)、a24(te)、a34(te)逐步增至1，说明随着有效役龄增长，系统最终将转移至完全故障状态.上述变化过程符合系统退化过程，随着有效役龄的增长，系统停驻在健康状态的概率越来越小，更容易转移至中间状态或非健康状态.当系统有效役龄达到最大值，系统将停驻在最终的退化状态.

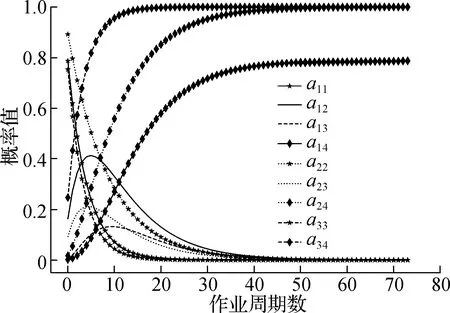
图7 时变状态转移概率值

同时，当t=0时初始状态概率分布π={0.85, 0.15, 0, 0}T，即初始状态下有85%发动机处于良好状态，15%为正常状态.航空发动机的最小维修成本c0和初始预防性维修成本c1分别为 3 012.13、301 312.03美元[20-21].

设预防性维修的改善因子α=0.85，正常工作状态的阈值(εs)和精度均为10-4，SEGA算法的种群规模为50，精英保留策略为锦标赛选择法，最大迭代步数为60，变异因子为0.5，交叉概率为0.5.如图8所示，当迭代步数为20时，种群的平均适应度函数已初步收敛；当迭代步数为60时，目标函数收敛至极小值，每个作业周期费用率为257 499美元.

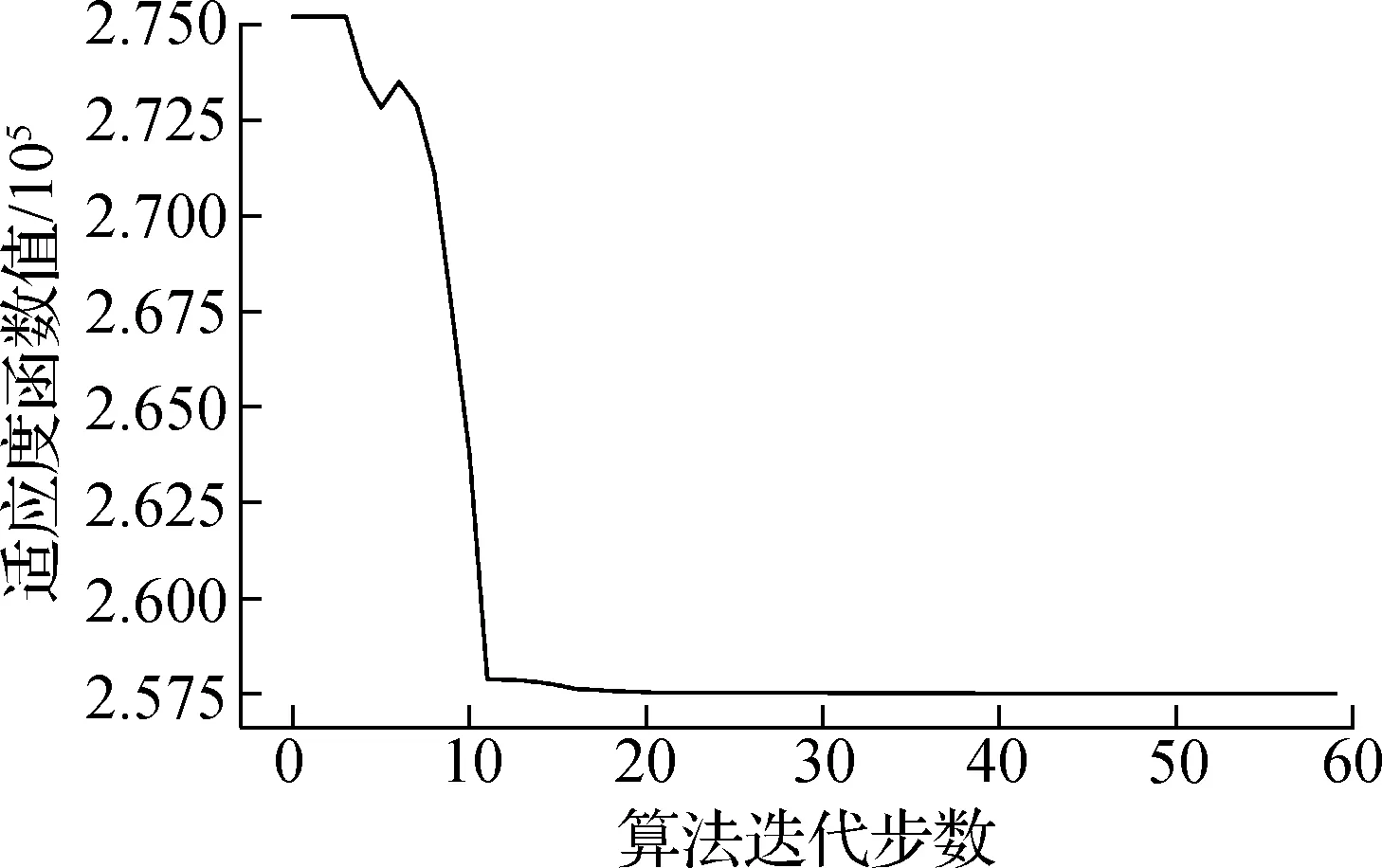
图8 算例优化的迭代过程

当迭代步数为60时，算法收敛至最优解.当初始预防性维修周期T1和维修总次数K分别为 13.79、19时，每个作业周期费用率为257 499美元.变量T1和K的种群方差分别为1.09×10-2和3.36×10-4.此时，精英个体充满种群内部，各个体对应的目标函数值收敛至最优值.

4 结论

1)考虑到传感器监测数据的噪声问题，本文采用EMD方法完成信号降噪并形成有效的退化特征量.

2)采用HSMM完成退化过程的时间序列动态建模，以多维特征变量描述设备退化状态.HSMM能有效描述各退化状态之间的状态转移关系，利用插值等方法可获得连续时间下的状态转移矩阵.

3) 基于HSMM的性能退化模型，采用役龄回退因子描述预防性维修效果，以单位时间维修费用率最小化为目标，构建维修优化模型.以某航空发动机寿命数据为例，采用SEGA算法求得初始维修周期、维修总次数分别为13.79和19，最小作业周期费用率为257 499美元.