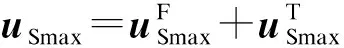考虑土与结构相互作用的建筑地下室抗震设计方法
邱滟佳 张鸿儒,2 于仲洋
(1 北京交通大学城市地下工程教育部重点实验室, 北京 100044)(2 北京交通大学土木建筑工程学院, 北京 100044)
地下结构的地震响应作为土-结构动力相互作用(SSI)问题的重要分支之一,在1995年大开车站发生严重破坏后[1-2],成为专家学者们研究的热点问题.与地上结构的地震特性不同,地下结构在运动过程中受到周围岩土的约束作用.Ramazi等[3]、Bhalla等[4]和Hashash等[5]发现地下结构在地震作用下随周围土体一起振动,加速度、位移等结构响应与周围土体基本一致.也正基于此,学者们提出了地下结构横断面地震反应分析的反应位移法[6-7]和地层响应法[8],用以分析地下结构的地震响应.
建筑地下室作为特殊的地下结构,其地震响应不仅有上述普通地下结构的特点,还受到地上结构的影响.Scarfone等[9]采用3维有限差分法分析了一栋20层建筑的地震响应情况,研究发现地上结构会在地震过程中产生较大的惯性相互作用;且根据Stewart等[10]的研究,地上结构的惯性相互作用与结构的自振特性相关.地上结构产生的惯性力作用在地下室上会造成其地震响应不再与普通地下结构相同.Borghei等[11]发现由于上部结构和基础的惯性作用,基础的实际振动并不等于运动相互作用下基础的振动,也就是说地上结构对地下室的影响是不可被忽略的.
然而工程中应用的各种抗震设计方法并不能综合考虑场地及地上结构对地下室的作用.目前对地下室的抗震设计一般采用基于地上结构的地震分析方法[12].这类方法将周边土体简化为土弹簧而仅仅考虑场地对结构的约束作用,这便忽略了场地对地下室的运动相互作用力;而如果采用常规的地下结构抗震设计方法[13],将建筑地下室看作普通的地下结构,便忽略了地上结构对其惯性相互作用力.显然无论是何种方法均无法准确分析地下室的地震响应.
为了得到一种更加安全、既能考虑周边场地对地下室的作用又能考虑地上结构对其影响的抗震设计方法,本文首先基于土与结构间相互作用的动力子结构法,从理论上说明建筑地下室的地震响应机理,然后参考地上建筑的方法计算得到上部结构的地震作用并将其作用在地下室上部,根据地下室的动力平衡特性推导得到满足上述要求的新方法.
1 建筑地下室抗震设计新方法
1.1 建筑地下室的地震响应分析
如图1所示带有地下室的建筑结构在地震作用下满足动力平衡方程:
(1)
式中,uT、uB和uS分别为地上结构、地上-地下结构边界和地下室在频域内的地震响应;PT、PB、PS分别为地上结构、地上-地下结构边界和地下室在地震过程中受到的外荷载;STT、STB、SBT、SBB、SBS、SSB和SSS分别为地上结构、地上-边界、边界-地上、边界、边界-地下室、地下室-边界和地下室在频域内的动刚度矩阵,频域内动刚度计算公式为[14]
S=-ω2M+iωC+K
(2)
式中,M、C和K分别为质量、阻尼和刚度矩阵;ω为频域分析中的圆频率.由于在地震过程中整个系统仅有地下室受到外部的地震作用,因此PT和PB均为0,故有
(3)
根据平衡方程组(3)中的等式STTuT+STBuB=0,可得
(4)
将式(4)代入平衡方程组(3)中的等式SSBuB+SSSuS=PS中,可得
(5)
从式(5)可以看出,地下室地震响应uS可分为2部分,即
(6)
其中
(7)
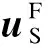
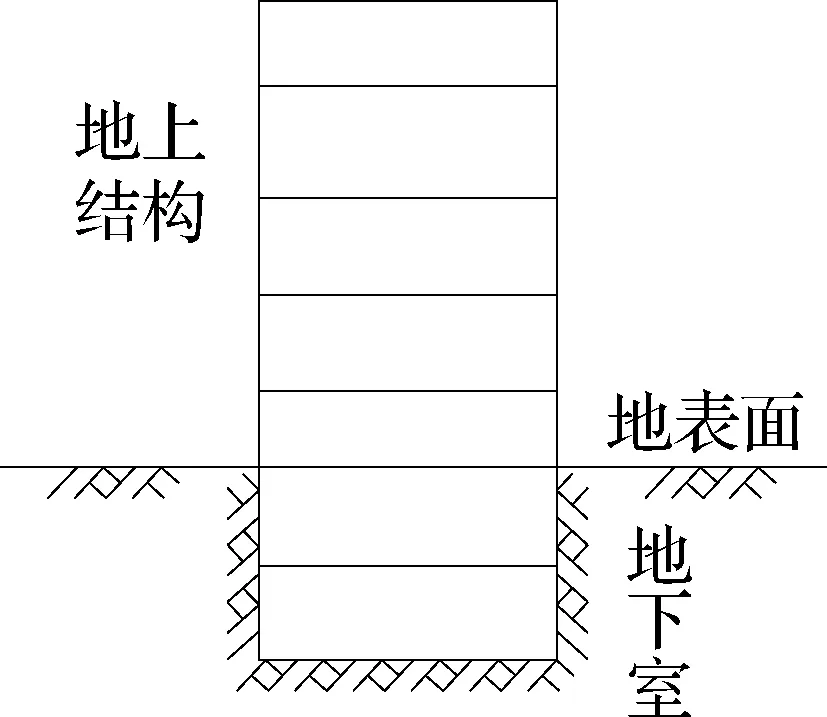
图1 地上-地下结构模型
显然无论是地下还是地上的抗震设计方法都无法准确地计算建筑地下室的地震响应,所以需要一种新方法既能考虑地下室与周边土体的动力相互作用又能考虑地上结构对其的影响,以保证地下室的安全设计.
1.2 新方法的推导过程
对建筑结构地上部分的影响进行深入分析,有
(8)
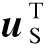
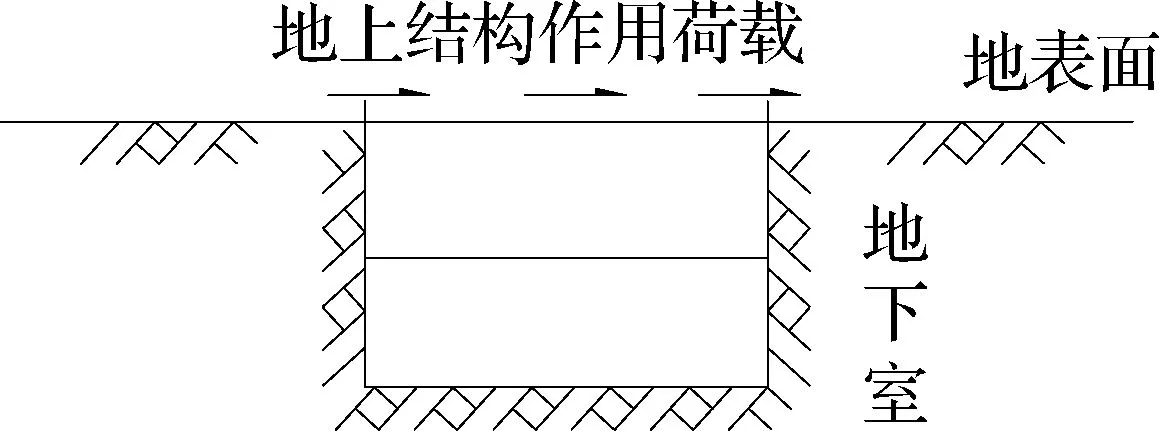
图2 简化分析模型
此时,地下室应满足动力平衡方程:
(9)
其中PB=QT,而根据土-结构相互作用的动力子结构理论[15]可知
(10)

(11)
将式(10)代入式(9)中得
(12)
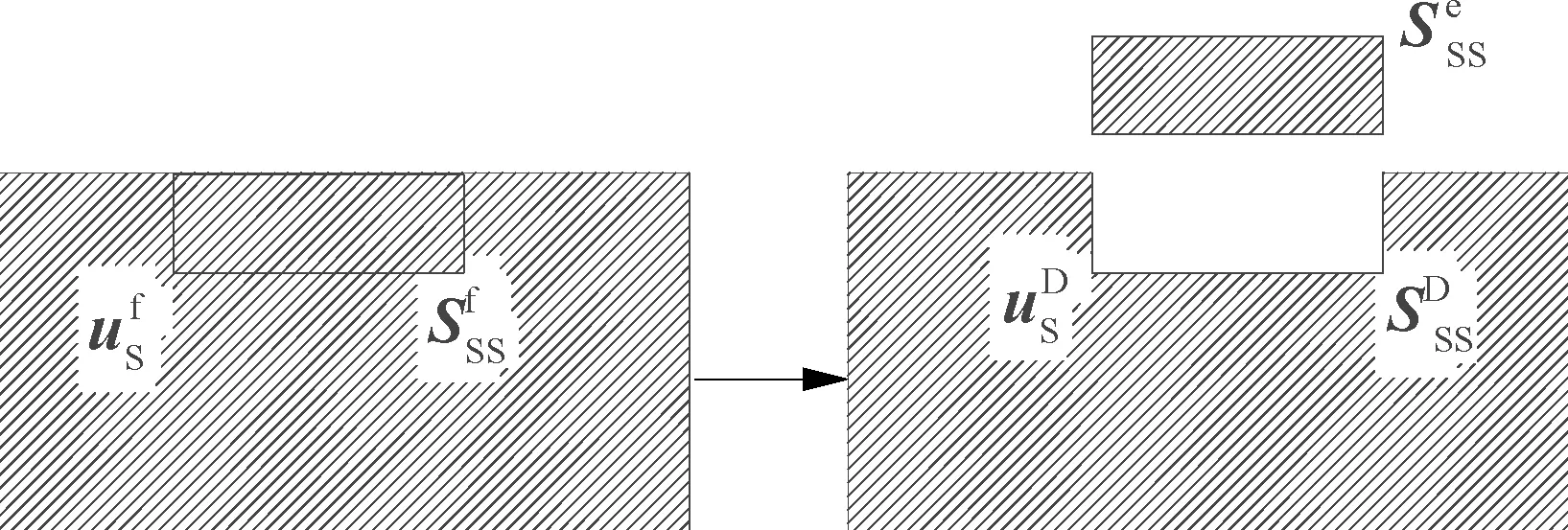
图3 土体系替换
(13)
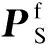
(14)
将频域内的动力刚度矩阵(2)和(11)代入式(14)中,并对公式两边作关于圆频率ω的傅氏逆变换,把频域内的动态平衡方程转换到时域内,即
(15)

由于抗震设计中往往关注结构响应的最大值,此时地上结构对地下室的最大地震作用荷载qTmax可由底部剪力法或反应谱法计算.在变形响应最大时刻,系统的速度等于0,所以可忽略阻尼项的影响.且根据以往的研究[4-6,16],由于场地的约束作用地下结构加速度与自由场同等位置加速度基本相同,即有
(16)
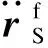
根据上述分析,式(15)可简化为
(17)
式(17)左侧是所需要计算的地震响应,右侧是计算模型上所需施加的地震荷载.根据该方程建立建筑地下室抗震设计新方法的计算模型,如图4所示.
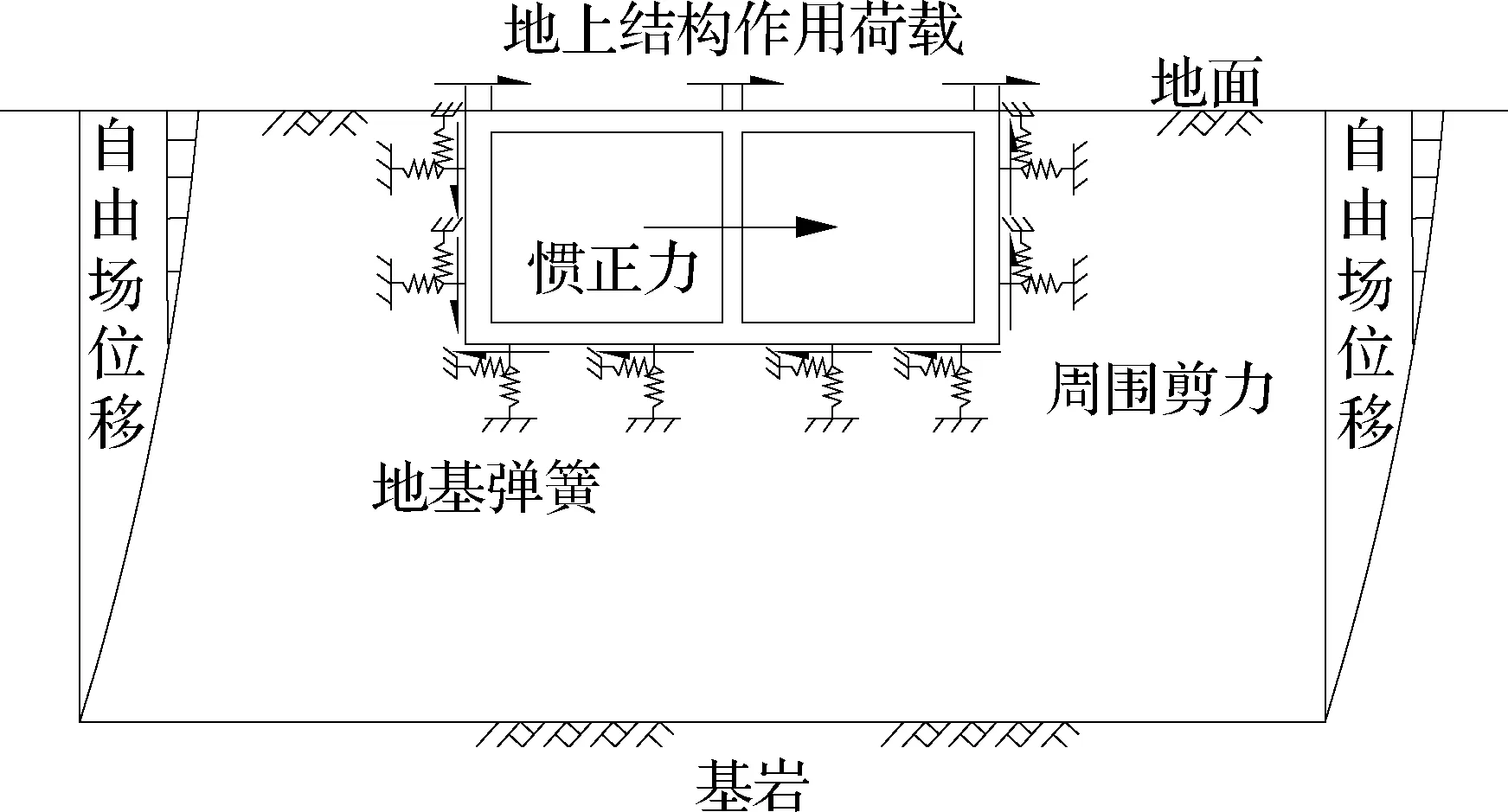
图4 建筑地下室抗震设计新方法
1.3 新方法的计算过程
将新方法的计算模型通过有限元软件编程计算,用于地下室的结构设计.新方法分为如下3步:
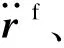
2) 利用底部剪力法或反应谱法计算地上结构的地震作用qTmax(包括底部剪力和附加弯矩).
3) 建立如图4所示的计算模型,并施加地下室加速度、结构顶底及侧边的剪力、自由场变形及地上结构作用在地下室的地震作用;然后进行静力有限元计算,得到地下室内力及变形响应.
1.4 新方法的适用性
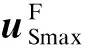
(18)
(19)
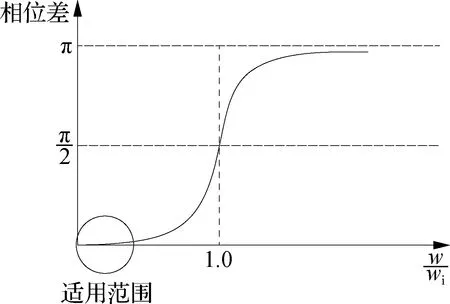
图5 单自由度系统的相频特性曲线
由于场地的过滤作用,最终作用在地下室的地震波频率一般为场地基频.根据上面分析可知,当地上结构基频较高或场地基频较低时才可采用新方法设计建筑地下室.
2 新方法的数值试验验证
为了论证新方法的正确性并确定其设计精度,本文对一系列有限元数值模型算例进行分析.以动力时程法为基准分析新方法的设计精度,并将其与地下结构设计中的反应位移法和地上结构设计中的反应谱法进行对比.所有的模拟均在ABAQUS2016中实现.
2.1 计算模型及单元设置
以标准断面(见图6)的建筑结构(地下室+地上结构)进行模拟分析,图6中序号1~6为内力分析的测点.其中地下室为2层3跨结构,地上结构为5层3跨结构.建筑整体为C35混凝土现浇结构,在分析中采用梁单元模拟结构构件,梁单元长为0.1 m.
地下室模型整体大小为200 m×50 m(见图7).为了能吸收结构产生的反射波,模型边界施加上黏弹性动力人工边界[19].场地土体为单一连续的饱和黏性土,采用等效线性动力本构[20]模拟土体动态应力-应变关系,黏性土的动态剪切模量比、阻尼比和剪应变关系曲线[21]如图8所示.场地土体采用2维平面应变的四边形实体单元(CPE4R)模拟,为了能更好地模拟出地震波在土体的传播,土体网格的大小n应满足如下公式[22]:
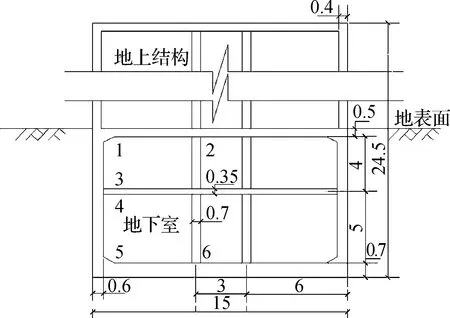
图6 建筑结构断面图(单位:m)
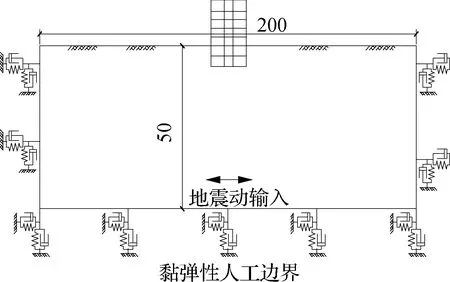
图7 动力时程模型(单位:m)
(20)
式中,cs为场地土体的剪切波速(本文为200、300和400 m/s);fmax为地震波最大分析频率(本文为20 Hz).计算可得土体网格必须小于1.25 m,本文模拟中设置为1.2 m.场地与地下室采用耦合连接.
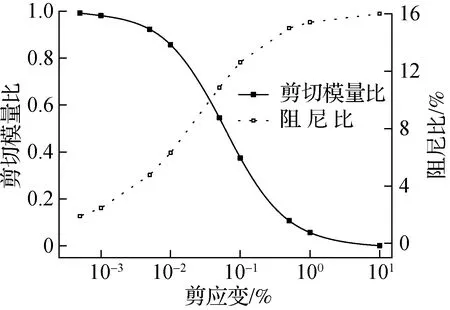
图8 剪切模量比、阻尼比与剪应变关系
2.2 地震动输入
地震动输入包括2条天然地震波(El-Centro波、Kobe波)和1条人工合成波(北京人工波),3条地震波的原始波形见图9.在分析中采取20 Hz的截止频率对原始地震波进行滤波处理,并且在基线校正后进行调幅处理使得输入不同地震波时地表最大加速度响应相同,3条地震波在5%阻尼下的加速度反应谱见图10.
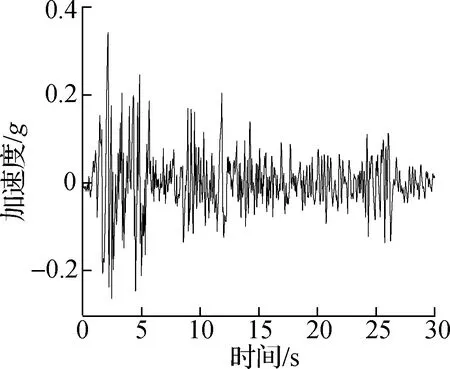
(a) El-Centro波
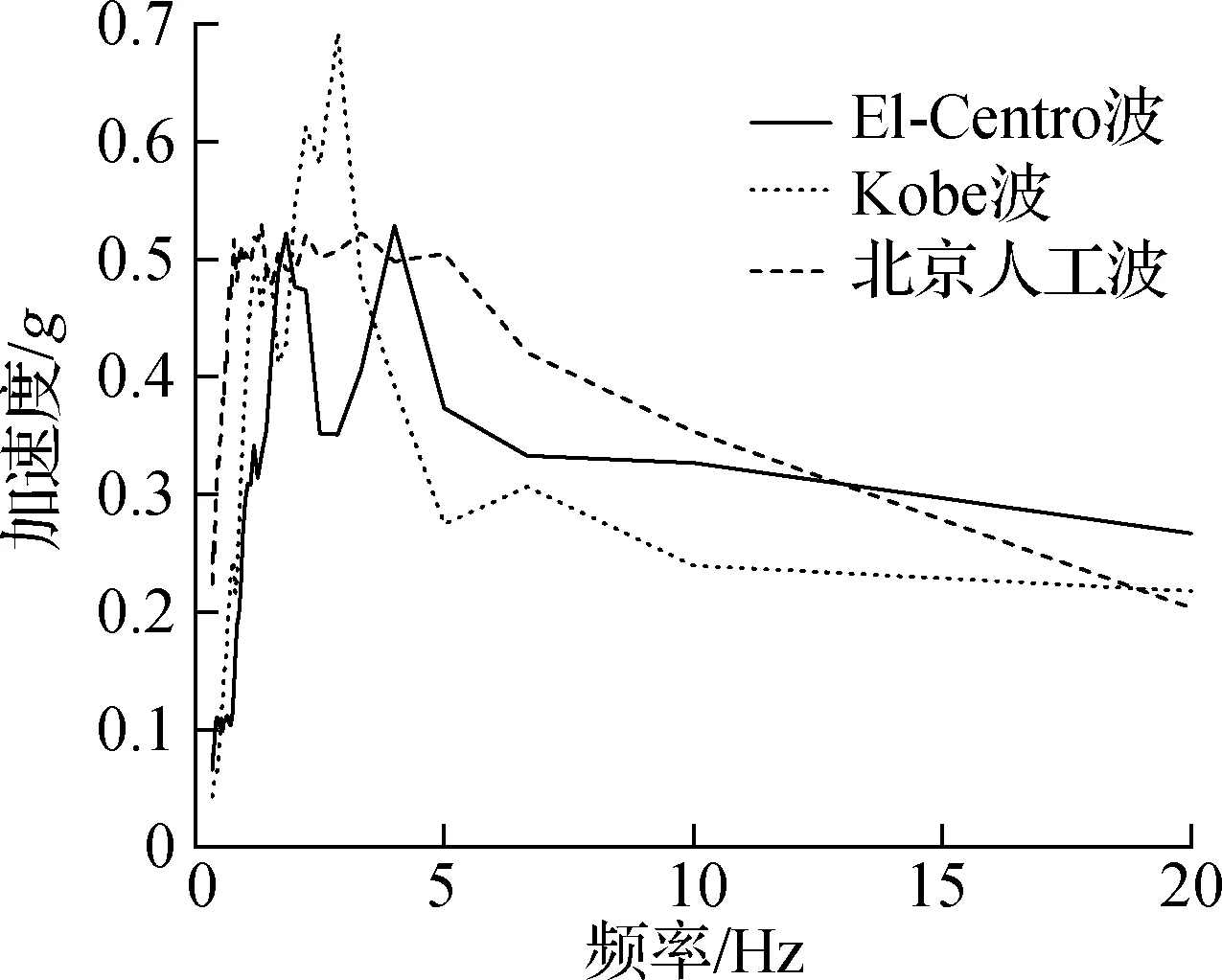
图10 3种地震波的反应谱
3 计算结果分析
选取抗震设计中非常重要的结构变形响应(层间相对变形)和内力响应(结构内力分析测点的弯矩、轴力和剪力)为分析对象,并以动力时程法的计算结果为基准探究反应谱法、反应位移法和新方法的计算精度.
3.1 不同输入波
不同输入波下4种方法在计算建筑地下室的变形响应及误差见表1.从表中可以看出:反应谱法和反应位移法由于各自分别没有考虑场地的作用和地上结构的作用,计算结果都偏小,其中,反应谱法计算首层变形误差一般在-20%左右,但其计算底层位移时变形误差非常大,达到了-70%以上,这显然相当危险;反应位移法的结果则相反,其计算底层变形误差在-20%左右,但计算首层变形误差达到-60%以上;本文提出的新方法结合了上述2种方法的优点,计算地下室首、底两层的变形误差能控制在5%以内.显然新方法无论是从计算精度还是设计安全性上均优于上述2种方法.
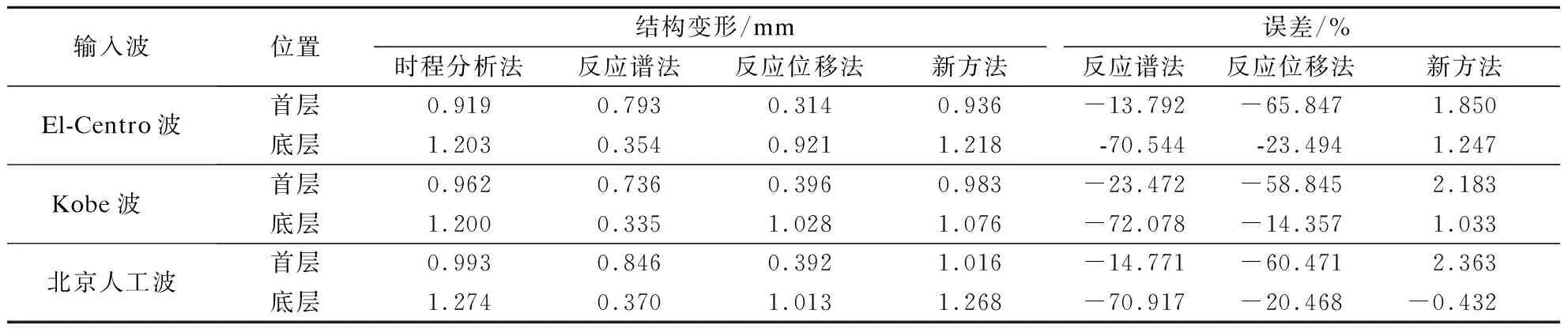
表1 不同输入波下的变形及误差
不同输入波下3种方法在计算地下室内力(弯矩、轴力、剪力)误差见图11.从图中可以看出:与变形响应相同,反应谱法和反应位移法的计算精度都相对较低.其中反应谱法在计算结构底层各点的弯矩时误差非常大,达到了-80%;反应位移法在计算结构底层的弯矩和剪力时相对准确,但是计算结构轴力和首层的弯矩剪力时误差很大,部分位置达到-95%,这显然是非常危险的.新方法在计算地下室内力响应时能控制误差在15%以内,计算精度远超上述2种方法.
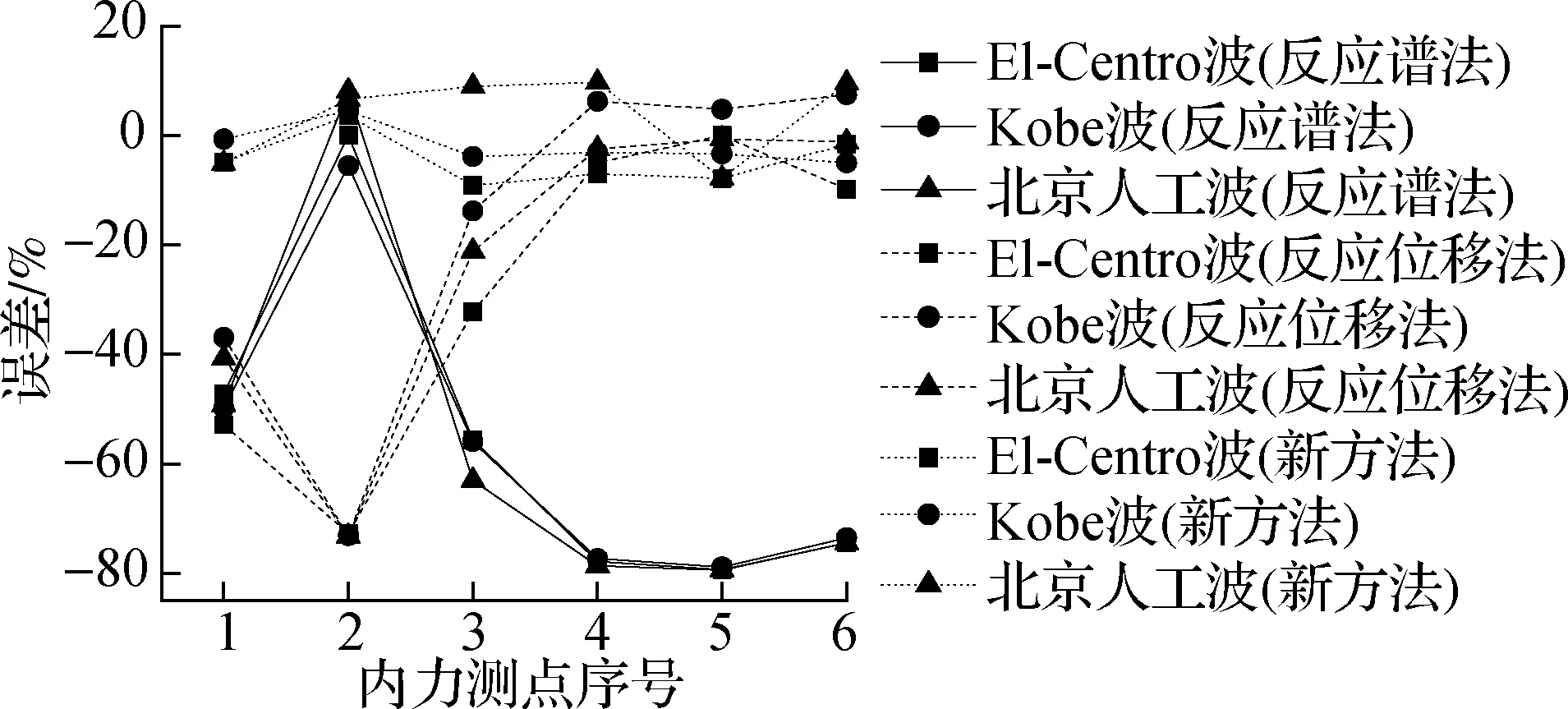
(a) 弯矩
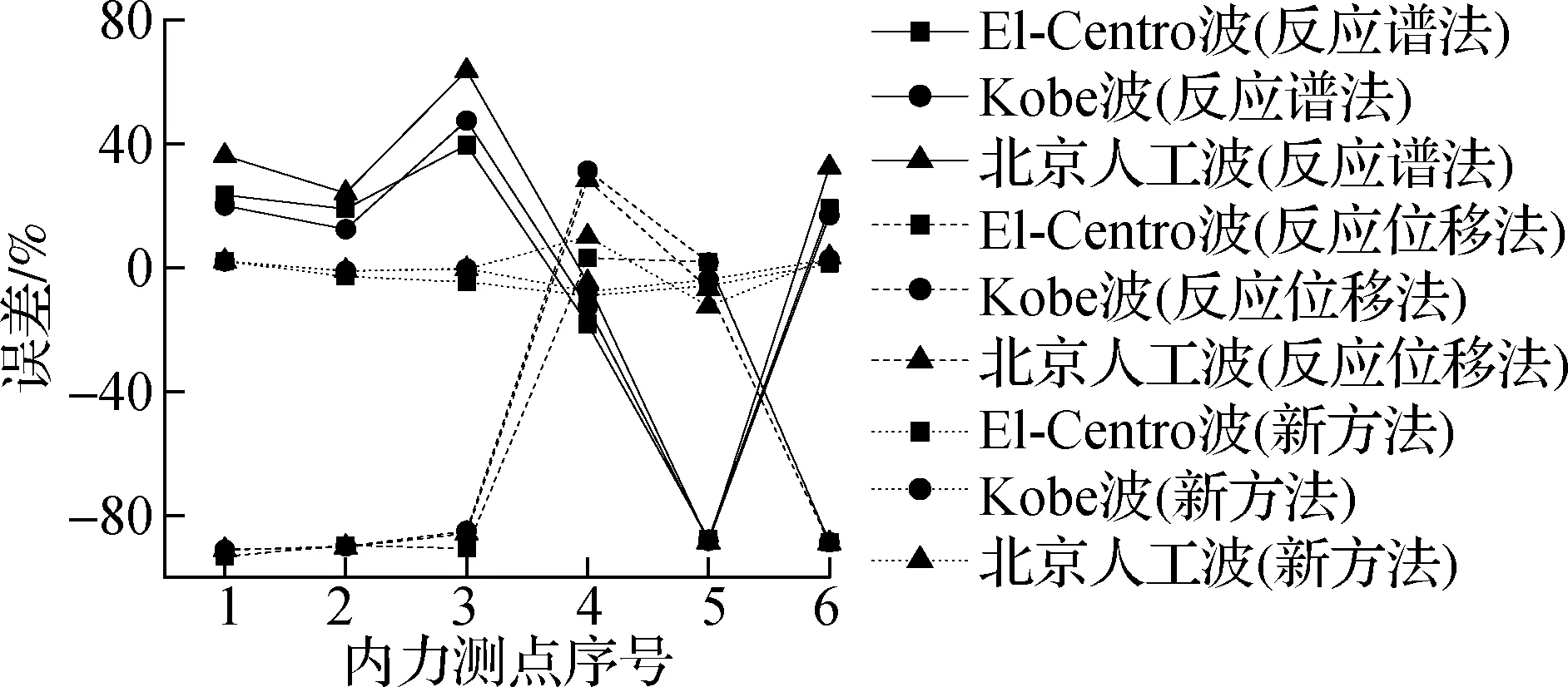
(b) 轴力
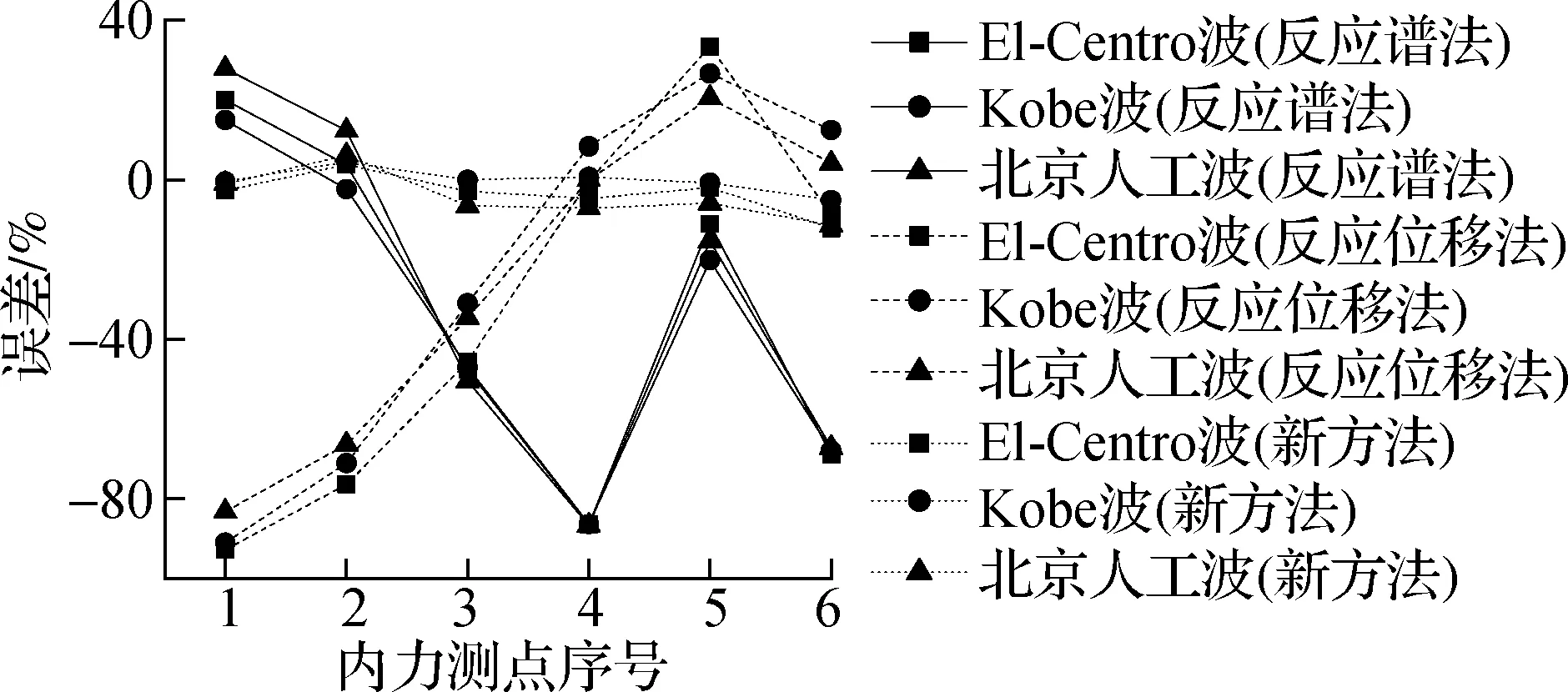
(c) 剪力
3.2 不同场地性质
不同场地条件下4种方法在计算建筑地下室的变形响应及误差见表2.从表中可以看出:与不同输入波的结果相同,反应谱法和反应位移法计算结果均偏小,两者在设计地下室时都偏于危险;相比于上述2种方法,新方法仍然有较为明显的计算精度优势.

不同场地条件下3种方法计算地下室内力误差见图12.从图中可以看出:与不同输入波的结果相同,反应谱法和反应位移法计算结果都偏小,两者在设计地下室时都偏于危险;相比于上述2种方法,新方法仍然有较为明显的计算精度优势.
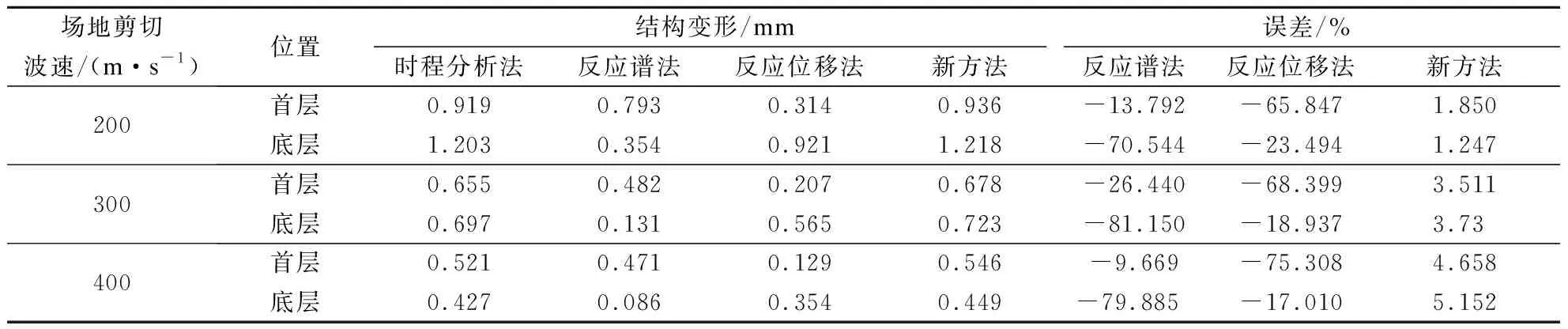
表2 不同场地下的变形及误差
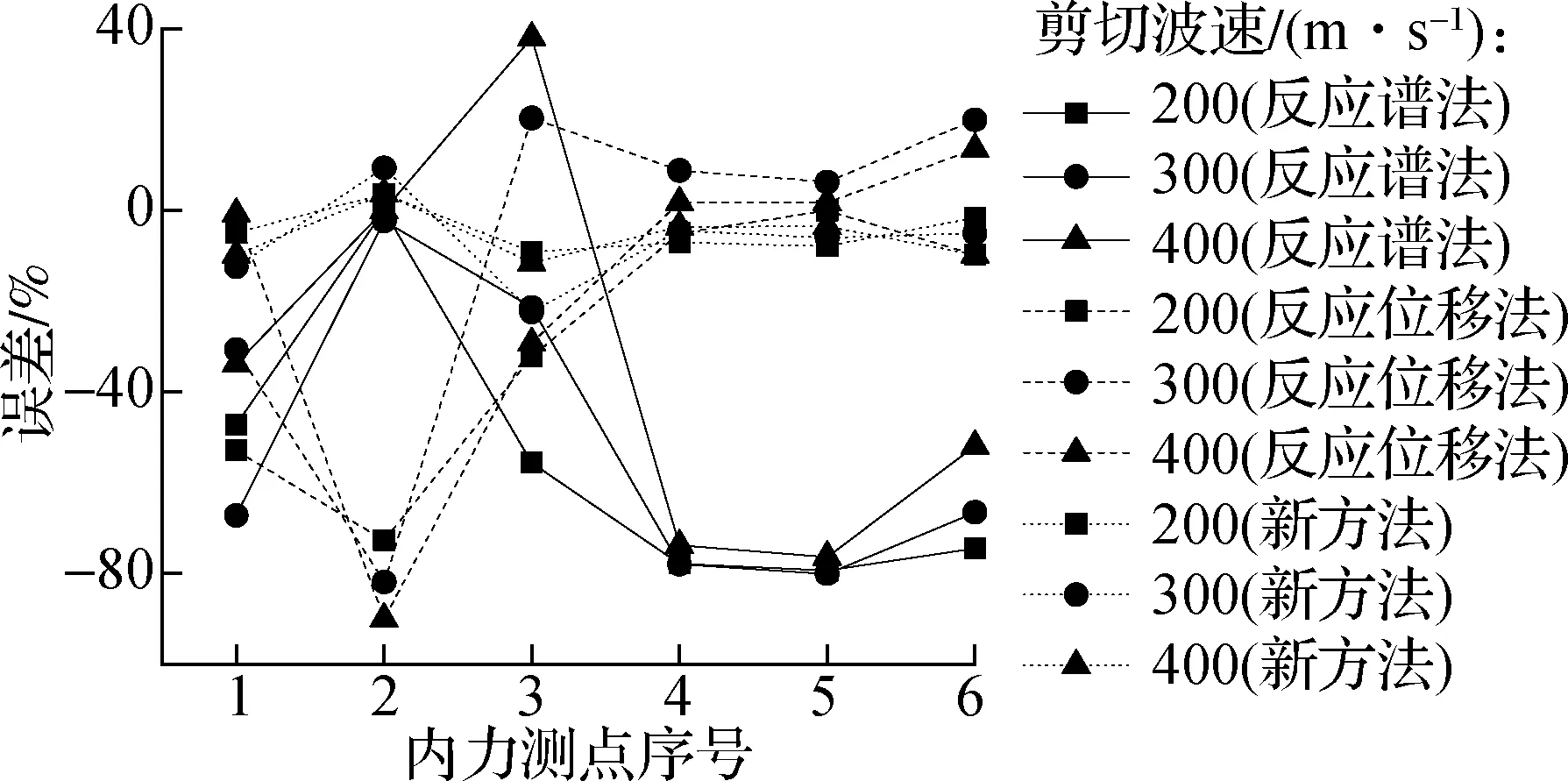
(a) 弯矩
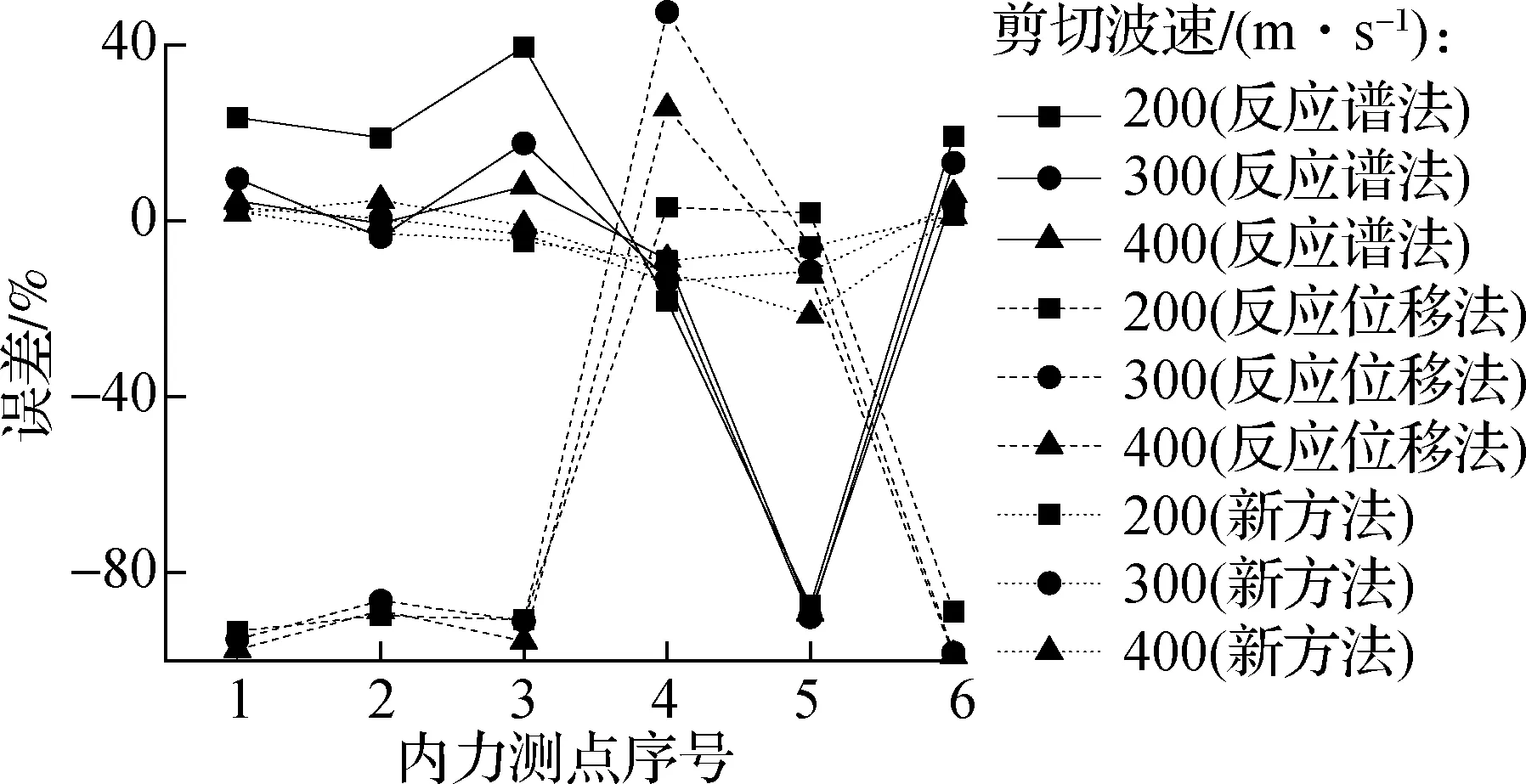
(b) 轴力
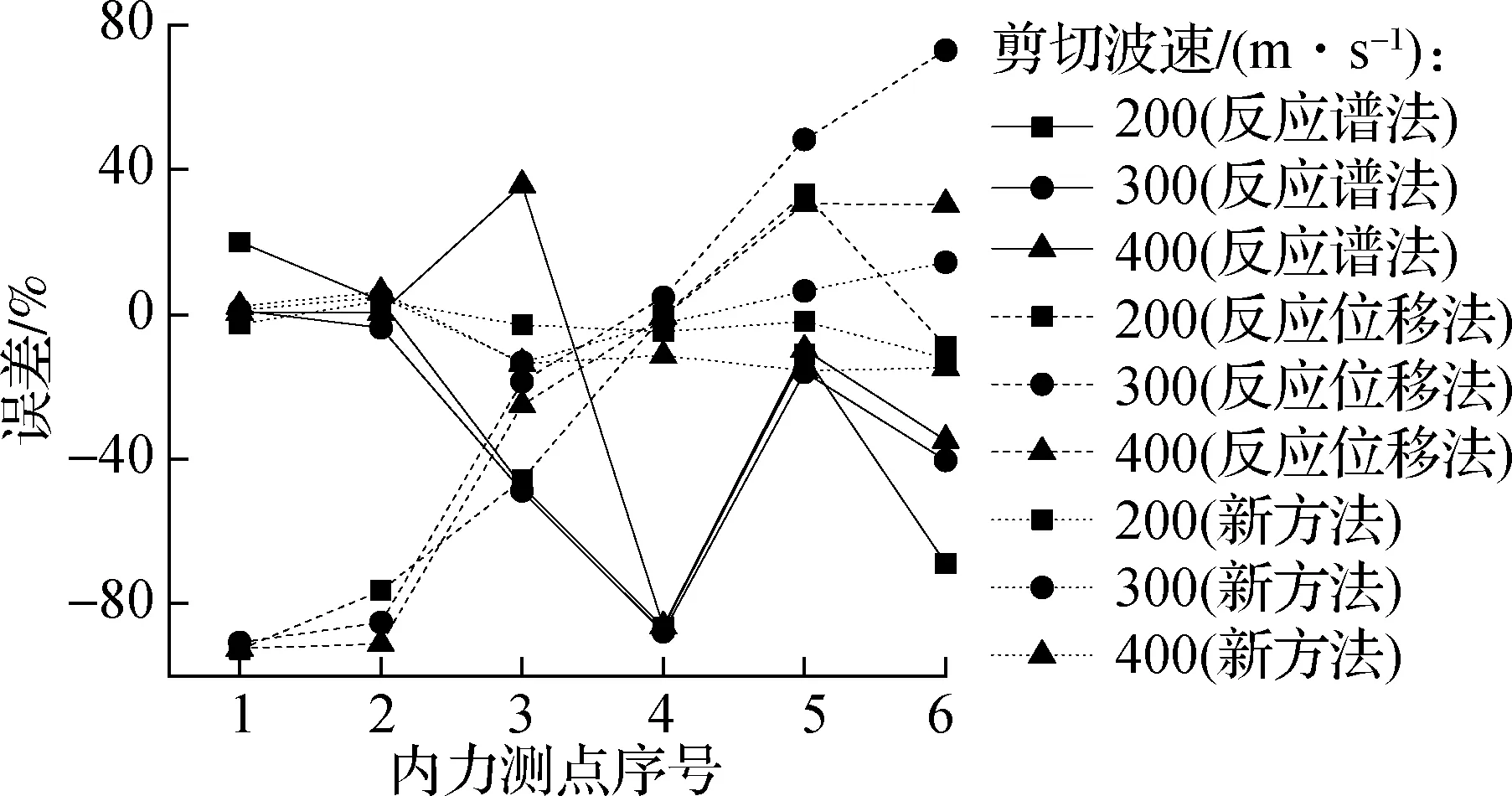
(c) 剪力
3.3 不同地震动强度
不同地震动强度下4种方法在计算建筑地下室的内力误差见图13,变形响应及误差见表3.与前面2种工况下的结果相似,无论是0.1g还是0.2g的峰值加速度,反应谱法和反应位移法由于各自分别没有考虑场地的作用和地上结构的作用,计算结果都偏小.相比于这2种方法,新方法具有明显的计算精度优势.
3.4 不同地上建筑层数
不同地上结构层数下4种方法在计算建筑地下室的变形响应及误差见表4,内力误差见图14.对于5层上部结构时,新方法无论是在计算结构的
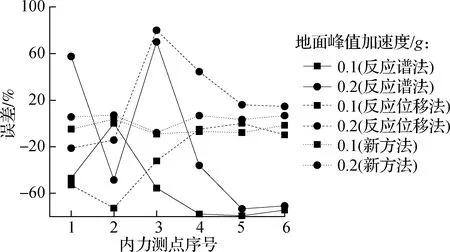
(a) 弯矩

(b) 轴力
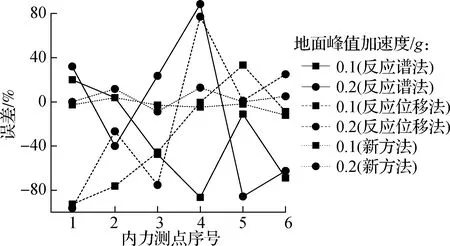
(c) 剪力
变形或内力都比反应谱法和反应位移法精确很多;但是对于10层的地上结构,新方法的计算误差明显增大,有些位置甚至不如反应谱法或反应位移法.
新方法在计算10层结构时误差增大的原因可从新方法的理论推导中看出:采用新方法设计地下室应满足地上结构基频较高或场地基频较低的条件.而当上部结构层数增加时,其自振频率降低,从而降低了新方法的计算精度.

表3 不同地表加速度下的变形及误差

表4 不同地上结构层数下的变形及误差
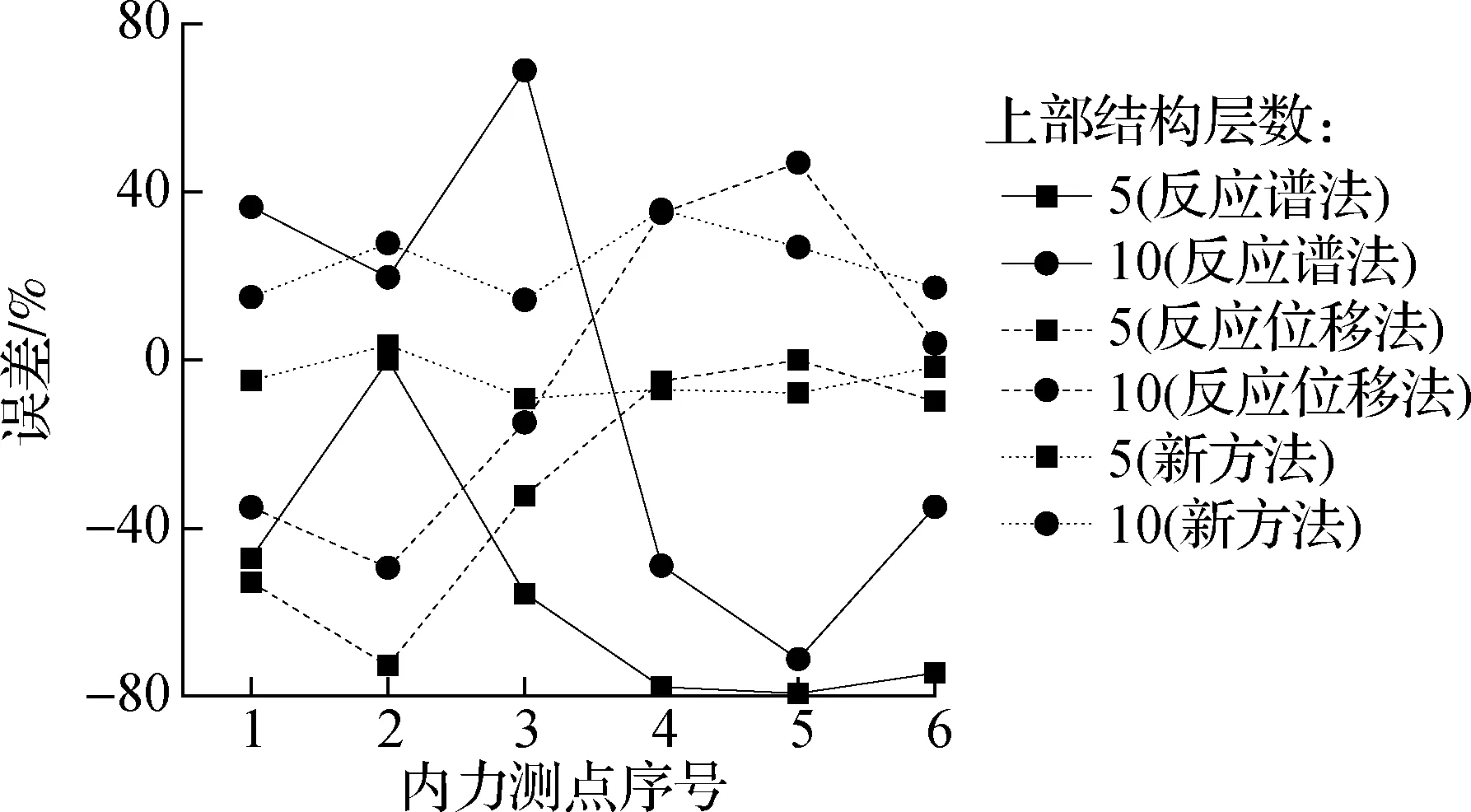
(a)弯矩
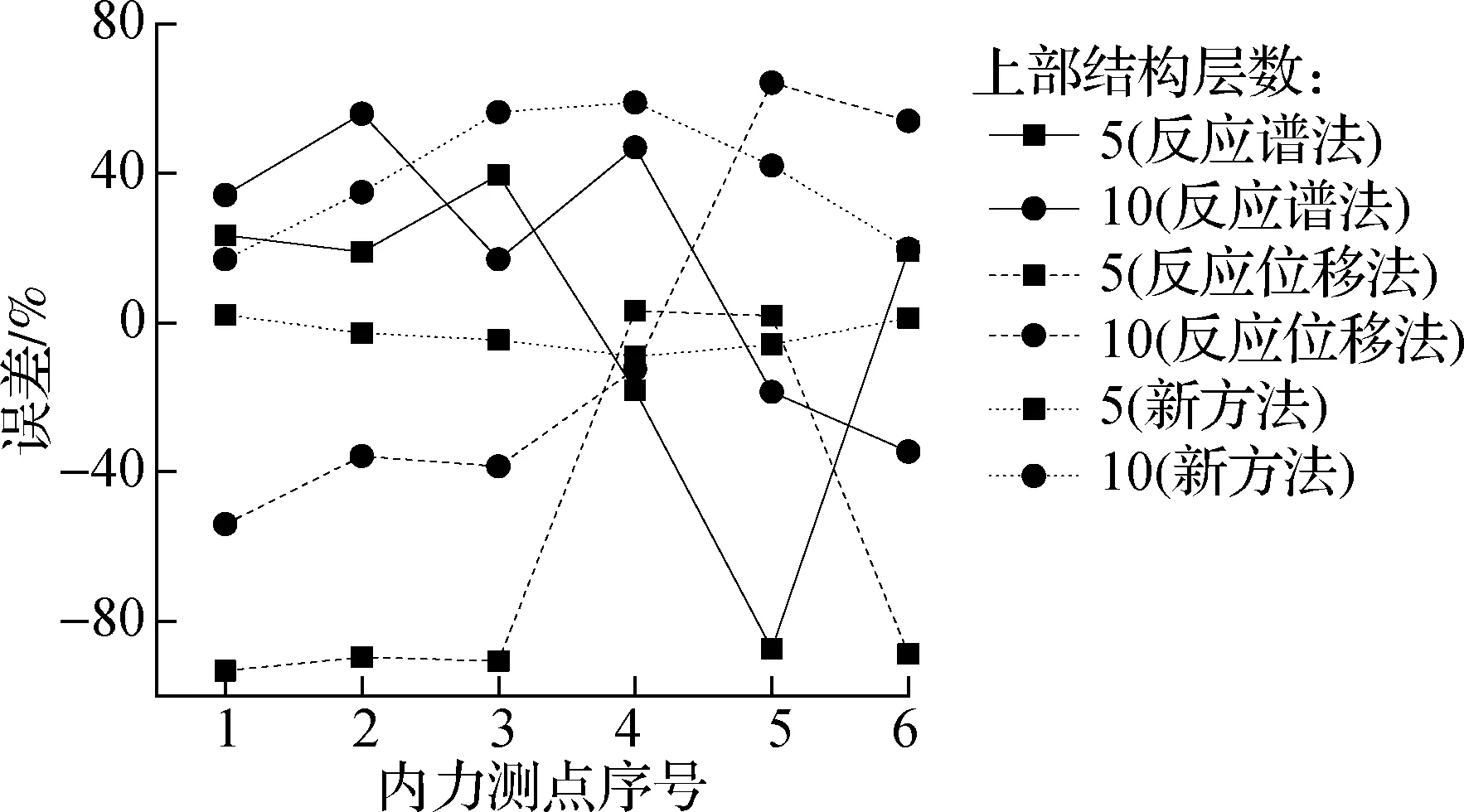
(b) 轴力

(c) 剪力
为了分析上部结构自振频率对新方法计算精度的影响,本文控制地上结构质量不变,通过改变刚度分析结构基频的影响.从图15的结果可以发现:在地上结构基频较高时新方法的计算精度仍很高,相对于反应谱法和反应位移法,新方法仍然具有较大的计算精度优势;但是随着地上结构基频减小,新方法的误差会有较为明显的增加,尤其是在结构基频低于1.5 Hz以后,新方法的计算误差显著增大,若此时仍采用新方法设计,那么结构就会过于保守.在结构基频高于1.5 Hz(一般对应7~8层混凝土结构的基频)时,新方法计算误差相对稳定,采用新方法设计结构无论是精度还是安全性都具有较大优势.
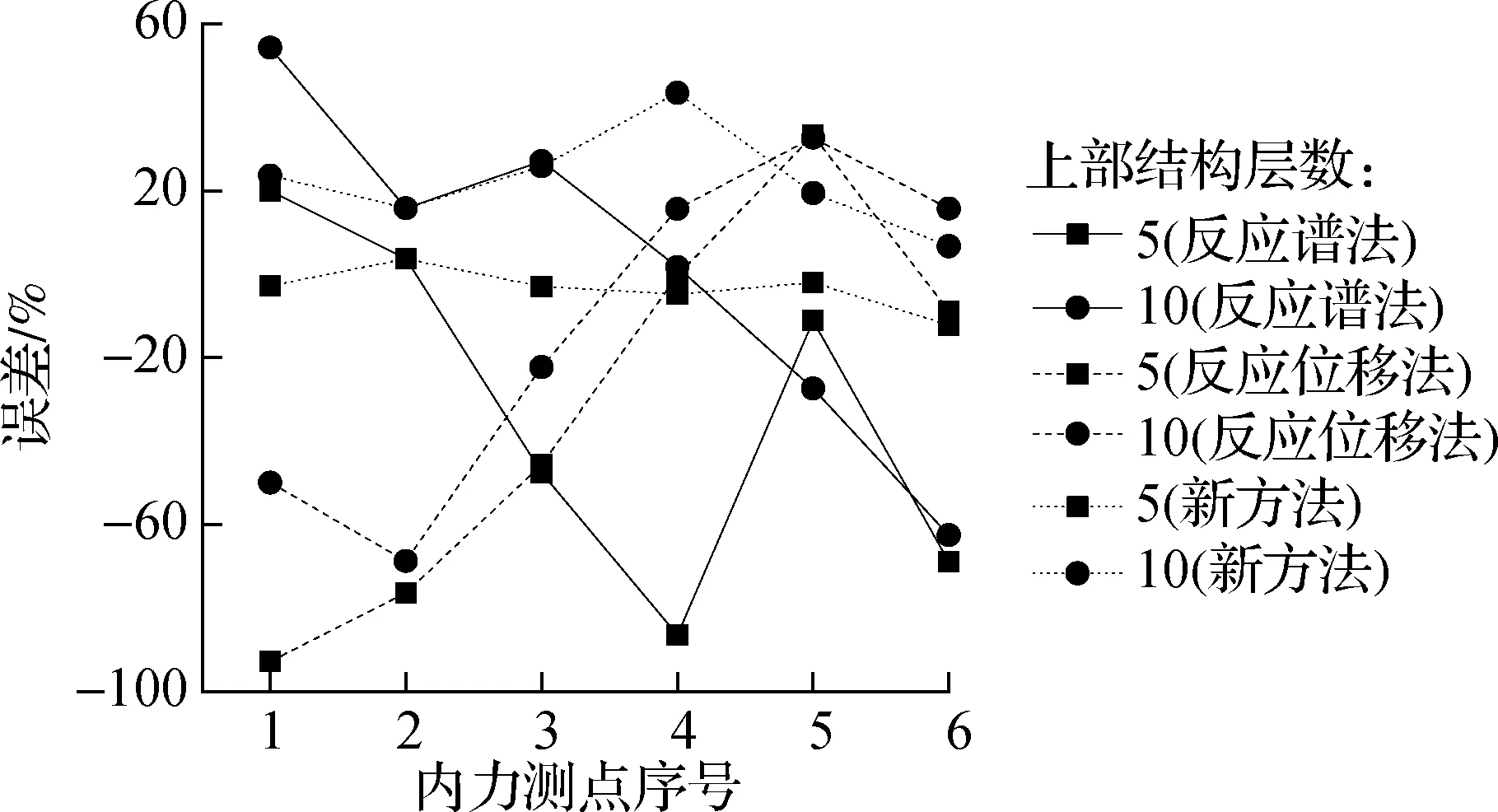
图15 结构基频的影响
4 结论
1) 基于土结构相互作用的动力子结构理论,分析了建筑地下室地震响应的特性,发现地下室的地震响应为场地对其的运动相互作用与地上结构对其的惯性相互作用之和,同时指出了现有方法对地下室抗震设计存在的问题:若采用地上结构抗震设计方法,就忽略了惯性相互作用;若采用常规地下结构抗震设计方法,则会忽略运动相互作用.
2) 将地上结构对地下室的作用简化为地震力,并以此为基础推导出一种既能考虑场地作用又能考虑地上结构作用的建筑地下室抗震设计方法.根据数值分析可知以动力时程的结果为基准,本文提出的新方法在分析建筑地下室的变形和内力响应时,计算精度都远高于现有的反应谱法和反应位移法.该方法是一种计算精度高且更加安全的设计方法.