人工智能与因果语言

吴小安 张 瑜

一、“迷你”图灵测试

人工智能的先驱之一艾伦·图灵曾提出这样一个问题[1]：怎么才能说一个计算机像人一样在思考？他给出了一个称为“模仿游戏”的测试方法（后来人们称之为“图灵测试”）：即向一个计算机提问，如果它对于问题的回答让我们不能区别和我们交谈的是计算机还是人，那么这一台机器就可以算是一个思维机器。当然要模仿一个成人的智能是困难的，随着教育和阅历的发展和推进，她的智能水平也一直在发展和推进。很自然的想法是不妨从模仿孩子的智能开始（“迷你”图灵测试），再循序渐进，最终实现成人的智能。

在珀尔和麦肯齐（Pearl and Mackenzie）[2]看来，对因果的理解是人类认知最普遍也是最不可或缺的一环。只有所造的机器人理解因果，我们才能把对于这个世界的所知教给它们。具体而言，在制造出一个理解因果的机器人之前，至少有两个疑难要面对：只有解决了它们，一个思维机器才是可实现的。首先，人们是如何从环境中获取因果知识的？其次，人们是如何处理因果信息的？第一个问题并不是珀尔关心的，他的主要贡献和努力在于回答第二个问题，即给出如何表征因果知识的方式，也就是因果贝叶斯网络，并说明这种表征方式如何使得我们能够快速地访问必要的信息并正确地回答因果的问题。

所以姑且把如何获取因果知识的困难放在一边，认为已经预存了如下的因果知识和模板（珀尔认为孩子的大脑并不像有些人所理解的那样是白板一块，而是已经有了丰富的机制和预存的模板）。图1表示了我们对于世界的因果认知和表征，季节的变化（SE取值{1，2，3，4}，分别对应春夏秋冬）会影响洒水器的开关（SP取值1 和0 对应洒水车的开关），也决定雨水的丰沛与否（R取值1 和0，对应雨水多与少），而不管是开洒水器还是雨水都会使得路面潮湿（W取值1 和0，对应路面潮湿与否），从而使得路面变滑（S取值1和0，对应路面滑与否）。

让我们从珀尔Pearl所谓的“迷你”图灵测试开始，一个“理想的”思维机器应该能圆满地回答如下问题：

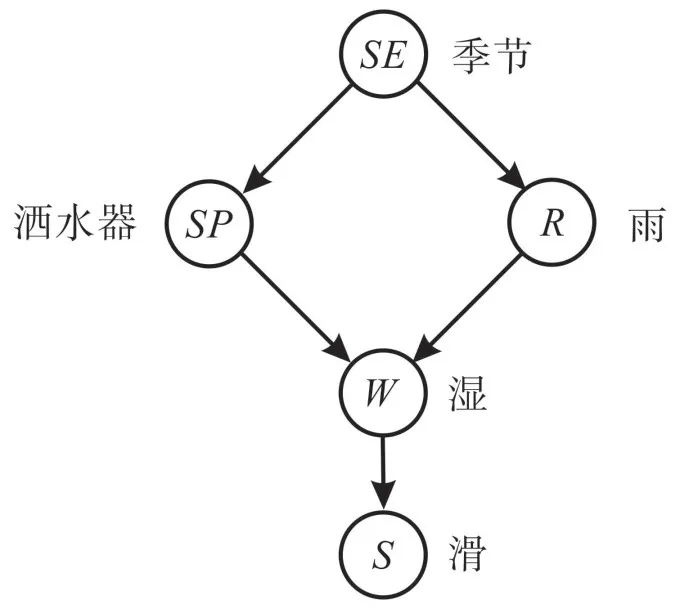
图1 表示五个变元之间依赖关系的因果图

问题1：如果此时正值秋季非常干燥的北京，但是有一处路面却很滑，这说明了天下雨了吗？

回答：并不太可能，更可能是洒水器被打开了，还有一种很小的可能性，路滑并不是因为路湿。而是因为其他原因。

问题2：如果我看到洒水车是关着的，那能说明天下雨了吗？

回答：那就很有可能了。

问题3：你的意思是如果在现实中我打开了洒水器，那么下雨就更不可能了吗？

回答：并不是这样的，你打开洒水器与否都不会影响是否下雨。

问题4：如果你看到洒水车是开着的且路面是湿的，那么设使洒水车关了，路面还会是湿的吗？

回答：路面将会是干的，因为当前是一个干燥的季节，下雨的几率很小。

上述因果图，以及以之为基础对于上述问题的回答，为真正智能的实现提供了思路。我们栖居在这个世界之中，在“烦”与“畏”中与之砥砺，慢慢地，对于这个世界如何周转运行，对于事物如何发展的内在理路和模式就有所掌握，对于上述问题的回答实质上就是以上述预存模式为基础，以新情况为根据对模式做必要之修正而得出的。但是如何让蠢笨的机器人能像人一样思考，回答起因果问题时从容不迫，在因果交谈中游刃有余，在珀尔看来就必须给它们装备因果推断引擎[2]12，[3]57，[4]160，装备了这个引擎的机器人，才能获取存储因果知识，并以之为基础做因果推断，进行有效因果交流，这个引擎中最关键的一环以及所有工作的初始就是：因果语言。

二、因果语言的源起

从一个颇具思维革命意味的、“测量金字塔”的例子来说明因果语言的意义和必要性是有帮助的。当别人问你“金字塔有多高？”假定你没有其他途径能查到金字塔的高度，我相信你不会想着造一个金字塔高的巨大尺子来垂直度量它，因为这样实在辱没了我们的教育，任何一个受过小学教育的人都知道欧几里德几何，都知道五条公设，并因而都证明过“相似三角形的对应边成比例”，如果你知道这个结论，那么测量金字塔的高度就不会那么耗时费力了。

你只要找到一个杆子，测量出杆子的影长（a）、杆子高（c）和金字塔的影长（b），再根据“相似三角形的对应边成比例”这个定理，就可以很轻易地计算出想要的结果。你会疑惑，这样一个人类在数千年前就知道的方法有什么值得大书特书的呢？这种方法的意义在于它昭示了人类思维的巨大胜利，只要倚赖创造的数学，就可以超越一些之前无法跨越的局限，只要在纸上计算一下，就可以得到在之前需要耗时费力才会得到的结果。

而今我们同样也面临这一类异常困难的问题：“吸烟是否导致肺癌”，或者“宏观政策的实施是否会导致通货膨胀”？对于这类问题的一个标准解决：良好设计的随机对照实验（randomized controlled trials）。在一个恰当的随机化对照实验中，除了一个因素（比如这里的吸烟变量或者政策变量），那些影响结果变量的其他因素，要么被固定，要么随机地变化，于是结果变量的改变必然是因为那唯一因素所致，以此求出我们想要的因果关系。

但是这个方法并不是包治百病的良方。首先，在很多时候，随机对照实验是不可能实现的（法律上、实践上、道德上、医学上，甚至经济上不可能）。比如下面这个实验在伦理上就不可行：随机抽样一拨人，随机指派为两组，一组拼命吸烟，一组完全不吸烟，然后观察个几十年，看最后哪一组患肺癌的概率更大一些；或者如果想要知道增加税收对于国家经济的影响，也不可能拿一个国家来作为实验对象，通过加税或者减税来观察对于国家经济状况的影响，代价太大，风险太高，也有太多的不确定。著名的1944 年的明尼苏达饥饿实验（Minnesota Starvation Experiment）在今天的伦理标准之下是断然不能进行的。其次，在执行随机对照实验的过程中，现实的复杂也远超我们的想象。比如研究观看暴力电视节目和学校霸凌之间的关系，很难有效地控制一个孩子看多少的电视节目，也近乎不可能知道是否有效地控制了看电视的时间。

所以，很自然的问题，我们是否有其他的方法或者程序，可以从可观测性研究（observational studies）中推导出想求的因果关系？在这种研究中，研究者只是记录数据，并不对研究本身进行任何干预或者控制，即只有数据集P（X，Y，W，…）。上述的讨论可以总结如下（表1）：

从表1中的比较知道，对金字塔高度的度量我们有两个问题是需要解决的：

1.需要一个相应的语言来表达需要表达的问题，在金字塔的例子中，把金字塔高度用抽象的符号d来表示；

2.还需要一个数学理论，能够以在手的数据求出因果关系，正如在金字塔的例子中，通过欧式几何，把金字塔高度的问题还原为通过一些相对容易可得的量（c，b，a）而计算出来。

表1 金字塔高度度量的启示

与之对照的两个问题珀尔[5]都给出了回答。他给出了因果语言来表征相关的因果问题，发展出结构因果模型来表征具体的情境，并通过干预概念把因果模型和刻画因果的反事实联系在一起（对于因果的反事实理论介绍与讨论，可以参看裘江杰[6]10-17、何朝安[7]3-9等人的研究），进而讨论诸多因果概念。

三、物理语言和概率语言

当然，因果从来不乏讨论。我们熟知的“穆勒五法”就是前现代因果研究的主导方法论，韦伯在《新教伦理和资本主义精神》中对新教伦理和资本主义精神之间因果关系的探讨（为什么资本主义在欧洲发生了，而没有发生在世界的其他地方？），所使用的方法就是穆勒归纳法中的“差异法”。这种探讨更多地依赖于作者本人的勤学苦读、广泛涉猎，形成的对于问题本身的直觉，然后再论证这种直觉的合理性。但是这种方法自有其学理上的弊端，更多是“一家之言”，受制于作者本人的视野和学识，并不具有科学的客观性。今天数据时代的到来，这种纯直观的学理研究必然是要扬弃的，数据来源的多面性和广泛性，使得我们有可能更加接近我们想要探寻的真实，在珀尔看来“数目是盲目的”（Data are profoundly dumb），它需要指导和引领，正如概率论源于赌博、运筹学的发展部分也是战争的需要，在当前新的形势下，传统的学科，比如社会学、政治科学、流行病学、公共健康也开始凤凰涅槃，对一种新的因果语言和方法论的需求迫在眉睫又势在必行。

1.语言的重要性

语言的重要性早就已经被行为科学家和心理学家所洞悉，他们论证说语言塑造人的思维方式和行为模式[8]。比如，在澳大利亚北部约克角城西边一个叫作波姆普劳（Pormpuraaw）的原住民小部落，这个部落里的人说库塔语（Kuuk Thaayorre），这个语言中没有描述相对空间位置的词，比如左、右等，只有描述绝对方位的词，比如东、西、南、北等。对比研究之后发现，使用绝对方向语言的人更精确地把握自己所处的方向。“事实上，他们这种能力之强，已经超出了科学家过去设想的人类所能达到的极限。正是在语言的强化训练下，他们获得了这种认知能力。”当作者在公开演讲时用同样的问题测试那些拥有相对方位语言的听众，他们对于自己身处之东西南北却异常晕圈。

珀尔和麦肯齐[2]10也特别强调语言的重要：“我对语言的强调也源于一个坚定的信念，即语言会塑造我们的思想。你无法回答一个你提不出来的问题，你也不能提出一个你没有词语来描述的问题。”正如像“引力”“熵”“量子”这样的概念，正是因为有了确切表达这些概念的语言，我们才能围绕这些概念发展出相关的科学和理论。

2.物理语言与概率语言

一个很自然的困惑，因果语言的提出是在21 世纪末叶，而彼时，科学的大树早已经根深蒂固，“絜之百围”，为何要大费周章，另辟蹊径，再创造一个因果语言？为何不就地取材，因地制宜呢？

遗憾的是，传统的数学语言表达不了所希望表达的因果问题。比如在物理学中牛顿第二运动定律是：

F=ma

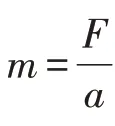
概率是许多特殊科学官方的语言，但是标准概率理论的词汇表中并不包含“原因”这个词。同样我们也不能表达“气压是气压计读数的原因”，“公鸡打鸣不是太阳从东方升起的原因”，因为它们和“气压计的读数依赖于气压”，以及“公鸡打鸣依赖（或者独立于）太阳从东方升起”是不一样的，所以两者的符号表征应该是不一样的。但是这个区分并没有在标准的科学分析中被严肃对待。尽管我们寓居于这个世界，用到太多太多因果的概念，但是迄今为止，还没有一个语言来形式化我们关于世界的因果判断。

于是珀尔提出用“do-算子”来表达因果关系，比如“吸烟是否导致肺癌”的问题可以形式化如下：

其中：

“do-算子”不只是旧的语言的扩充，更是新的语言的开始。如果你刚刚接触统计学，会很难理解它对于因果概念的敌意，比如很多统计学教材开篇都会强调“我们这本书中不会使用‘因果的’或者‘因果’这样的词汇……我们这样做是出于一种谨慎，因为从研究中我们很少能够得到关于因果的靠谱结论”[9]。在珀尔看来，之所以有这样一个对因果的排斥是因为没有与之对应的语言来表达我们想要表达的因果关系，统计的语言是概率，但是概率却不足以成为因果的语言。

3.因果语言的特点

我们需要对这个新的因果语言做一些澄清。首先，我们需要说明这个新的语言和概率之间的区别与联系；其次，我们需要阐述清楚，这种新的语言实现什么样的目的，即这个新语言的使命在哪里，以此，才能发展出与之相应的数学来实现这个目的；再次，将说明这个新的语言对于人工智能和其他研究的意义。

当然，引入一个语言是一回事，正如表（1）所指出的，另一个困难的地方在于，要给出相配套的数学理论，让它和数据结合在一起，把之所以引入这个语言的那些基本想法很好地体现和贯彻出来。“物有本末，事有终始”，姑且把这个困难的问题先搁置在一边，先把因果语言的问题讲清楚。

首先，需要看到这个新的因果表达式和条件概率的区别：

P（Y=1|do（X=1））≠P（Y=1|X=1）

“相关并不意味着因果”（Correlarion is not causation），早上公鸡打鸣，太阳随后就会升起来，这两者之间有相关关系，但是公鸡打鸣并不是太阳升起的原因，它们之间没有因果关系。

具体而言两者的区别有：首先，是方向性。因果是单向的，只有原因会影响结果，结果是不会影响原因的。但是概率公式是对称的，根据贝叶斯法则，可以从P（Y=1|X=1）得出P（X=1|Y=1），反之亦然。

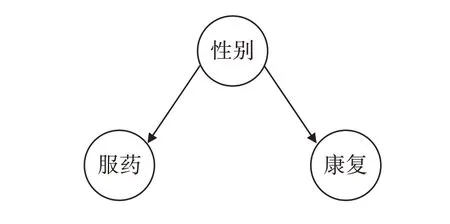
其次，是混杂（即共同原因）。我们求条件概率，比如P（康复|服药），我们首先要知道服药的人数是多少，然后再从中找出服药且康复的人是多少，后者除以前者得出的结果就是我们所要求的条件概率。但是这种条件概率并不能满足我们需要理解因果关系的目的，因为可能存在混杂因素，它既影响病人服药也影响病人的康复（比如性别），所以哪怕你得出P(康复|服药)=1，也并不意味着服药是康复的原因。而因果关系实际上表示的是服药这个行为对于康复的影响，如何来刻画这种行为对结果的影响？显然它和上述条件概率的直观不尽然相同。

从现实的生活中，也很容易认识到观察与干预之间的区别，比如我们都能感觉到人的手掌的大小和他脚掌的大小之间有一种相关关系，脚大的人手一般也不会小，所以一般而言：P（Y=y|X=x）不等于P（Y=y）。P（Y=y|X=x），“∣”的右边是通常的概率演算中的条件化，代表的是证据化条件“假如我们看到”，反映的是在X取值为x的那些个体中，Y的总体分布是什么。注意，当条件化一个变量的时候，并没有改变系统，只是使变量取了我们感兴趣的值，从而把关注点转移到感兴趣的那一类情形中去了（实际上就是一种筛选），如果要谈改变的话，那改变的是我们对于这个世界的感知，而不是这个世界。

但是如果你从小就裹脚，显然你的脚可能就停留在某一个尺寸了，但是你的手掌还是会正常发育，大小不会受到太大的影响。裹脚就是一种干预，但是裹脚对手掌的发育并没有因果影响，所以P（Y=y|do（X=x））=P（Y=y），即不管裹脚与否，手掌大小的概率并不受影响。P（Y=y|do（X=x），“∣”的右边是do算子，代表的是因果条件“假定我们干预了（doing）”，反映的是如果在总体中的每一个个体它们的X的取值为x，那么Y的总体的分布是什么。当干预一个变量时，我们固定它的值，改变了这个系统（即珀尔所谓“手术式的”干预），其他变量的值也可能因为这个值的改变而改变。

在因果模型的理论中，当我们通过干预来确定某个变量的值的时候，与之对应的图表达的就是对图的外科手术（surgery），删除所有指向这个变量所对应的节点的箭头，并把这个节点所代表的变量的值固定为干预的值，由此我们得到了被修改的因果模型（perturbed causal model）。

尽管引入do-算子只是一个开始，但那却是打开新世界的钥匙。珀尔[5]422生动地指出，如果你身处16 世纪，你是一个加法（“+”）运算的专家，迫切感觉需要引入一个新的算子来简化多个相同的数字相加的情况，因为把这个相同的数字一个一个加起来实在是太繁琐笨拙了。你所做的第一件事情就是用一个新的符号来表达这个过程：×，然后你要穷究这个算子的意义，正如你推导出的很多加法的法则一样，你也希望推导出与乘法相关的法则，比如分配律、结合律、交换律等，并说明它与之前的加法运算之间的关系。同样，我们引入了一个新的do-算子，要说明这个新的算子和条件概率之间的关系，以及怎么来计算它，以得到想要的结果。为此需要一个与之相配的理论，在金字塔的例子中我们有欧式几何，那么在这个新的因果语言之下，要给出什么样的因果理论呢？那就是结构因果模型。接下来我们将对do-算子的用处做进一步的刻画，而这需要通过把它与随机对照实验中“随机化”这个概念做一番比照。

总之，观测和干预对应着两种处理数据的方式。条件概率P（Y=y|X=x）对应的前一种，一堆数据在我们面前，我们观察那些X=x的数据，看在这种条件下Y=y的概率是多少。但是概率的语言和因果的语言还是有很大不同，比如因果是单向的，而条件概率本身并不具有方向性；且当一个共同因素（比如Z）决定另外两个因素（比如X和Y）时，我们知道X的改变并不会导致Y的改变，但是在概率中并不能体现这种特性，这也就是为什么要扩充概率的语言，引入do-算子的原因（注意，这里我们对于因果持一种操控主义的理解[10]，原因是某种产生差异的东西，改变原因就能改变结果）。

四、因果语言与随机对照实验

正如在第二节所指出的，因果模型的提出是为了补随机对照实验之憾，挽随机对照试验之弊。但是因为模型本身有很多很强的假设，比如从数据中发现因果结构的“桥接原则”（bridge principle）（对于它的介绍可以参考杨仁杰[11]18-25），讨论的模型是马尔可夫或者半马尔可夫模型，以及用不多的变量及其决定论方程来模拟一个复杂的机制。它能否成为一个合格的“替代”，有待时间的检验，但是不妨先把这些疑虑放在一边，从一个简单的例子来说明因果语言所要刻画的随机对照实验的原理为何。

表2 是观察数据，从中我们发现一个奇怪的现象，如果分别考察男性和女性服药之后的康复情况，我们发现不服药更有利于康复，但是如果考察总体的数据，得出相反的结论，服药有利于康复。当然敏锐的读者立刻就会发现其中的问题，观测数据受性别的影响，女性更倾向于服药，而男性更不倾向于服药，而性别的差异又会影响康复，所以可以把我们从表2中所读到的这些因果假定用图2表达如下：

令X=1 代表的是服药，Y=1 代表的是康复，Z=1 表示的是女性（Z=0 表示的是男性）。显然Z混杂了X对于Y的因果影响，如果要求出X对于Y的因果影响，我们要控制Z。

表2 观测数据（关于药物的例子）

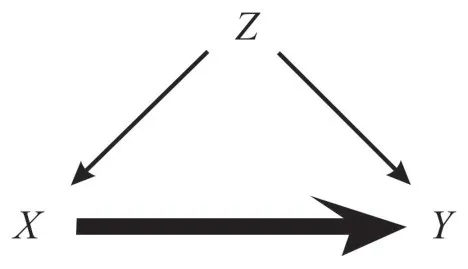
图2 与数据一致的因果图

在实际的随机对照实验中，如果认定混杂因子是性别（Z），就要把总体按性别划分，再在男性总体中随机指派他们进入处理组（treatment group）和对照组（control group），在女性的总体中随机指派他们进入处理组和对照组。

随机对照实验所做的就是破坏Z到X的因果机制，让X对于Y的直接因果效应彰显出来。为了实现这样一种破坏，比如可以通过抛硬币这样一个随机过程来决定被实验者是服药还是服用安慰剂，由此把那些可能影响服药的因素，比如本例子中性别的因素，还有在其他一些情形中的比如教育水平和健康保险等等影响服药的因素给排除掉，使之不再影响是否服药。

对应到我们的因果图3（这里可以把因果图理解为数据的生成机制）中把Z指向X的箭头删除，这种把随机化和因果图中对应箭头的删除联系在一起的直观并不是显然的，正如珀尔[5]244所说：“在听了他斯波蒂斯（Peter Spirtes）在瑞典的乌普萨拉（Uppsala）发表的一个演讲之后，我（珀尔）第一次意识到，执行干预①对于“干预”有不同的理解，伍德沃德（Woodward）[12]认为应该把干预理解为一个因果过程，它独立于模型中的其他变量而起作用。而刘易斯（Lewis）[13]则把这种设定变量值的干预理解为一个小“奇迹”（miracle）。可以被看作从因果图中删除箭头。”

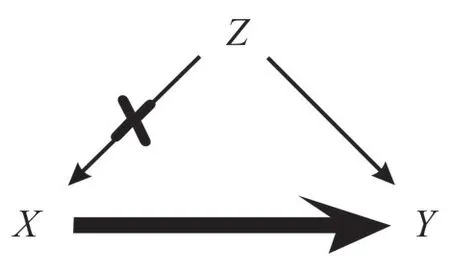
图3 随机指派的作用

正如前面金字塔的例子，我们不需要耗时费力来测量金字塔的高度，只要用相对容易得到的数据在纸上算一算，就可以求出金字塔的高度。同样地，当面对因果问题，也希望不需要做随机对照试验，或者在因为各种阻力不能做随机对照实验的时候，结构方程模型能拥有欧式几何那样的效力，我们只要数据在手，算一算即可求出所要求的因果关系。根本上，我们是比照着随机对照实验来设想因果语言的，它的主业是成为社会科学研究的方法论，它人工智能的蕴含更多是上述工作的引申。

五、总结

有了我们前面所讨论的因果语言，就可以把上述因果问题用它来表征如下：首先，问题1 和问题2 是经典的概率问题。问题1 所说的是，如果季节是秋季且路面很滑的情况下，天下雨的概率有多大，可以形式化为：P（R=1|SE=3，S=1）；问题2 所说的是，如果在秋季，路面很滑且洒水车又关着的情况下，天下雨的概率有多大，可以形式化为：P（R=1|SE=3，S=1，SP=1）。只要有上述图1，以及与图中节点相应的变量的条件概率表（两者组成了一个因果贝叶斯网络），那么根据贝叶斯定理很容易就可以回答上述问题。需要注意的是，上述两个问题都不是因果问题，只是一种回溯推理（Abduction），根据概率就可以得到想要的结果。

问题3 和问题4 则是典型的因果推理问题。问题3 属于“展望式”（prospective）反事实，判断的是一个行动对于一个变量的因果影响，即打开洒水车（do(SP=1)）是不是会对下雨有因果影响，问题可以形式化为：P（R=1|do（SP=1））。问题4属于“反省式”（retrospective）反事实，在给定路面是滑的且洒水车开着的证据之下，如果反事实设定洒水车是关着的，看对于里面的滑有无因果影响，问题可以形式化为：P（W_｛SP=1｝=1|SP=0，W=0）。根据珀尔的结构因果理论，贝叶斯网络加上do-演算就可以回答问题3。但是对于问题4的回答要困难很多，要对事物运行的机制有深刻的理解才行，即需要知道对应变量确切的结构方程，以之为基础，根据珀尔[5]206，给定确切的因果模型M，反事实P（W_｛SP=1｝=1|SP=0，W=0）的判定可以通过如下三步来实现。首先是溯因推理，根据证据{SP=0，W=0}来确定变量SE的概率或者确定的值；其次由表示反事实前件的行动do(SP=1)来修正模型M，得到子模型MSP=1；再次，通过得到的子模型和由证据所更新的SE的信息来计算反事实后件的值，并最终确定反事实的概率。显然地，do-算子在上述问题上的形式化表述中扮演着重要作用。

需要注意的是，首先，一旦给出数学机制，实现上述过程的算法就不再那么困难了。但是也并不意味着珀尔意义上的智能就是唾手可及。人工智能是一个非常宽泛的领域，因果推断只能算是其中认知与推理工作，或者自然语言理解与交流工作的一部分（对于因果推断在人工智能大图景中的地位和作用可以参考：梅剑华[14]86-95），而本文所介绍的因果语言及其直觉、特点和作用更多是一种蓝图性的指南作用，它只是一个支点，如何让机器人真正具有智能？数学的设想在工程上如何可行，如何贯彻？还需要多领域跨学科的合作与努力才行，总之，前路茫茫，任重道远。

其次，任何一个因果理论要配享“理论”之名，至少有四个方面的工作需要完成，首先，以数学的语言来表征因果问题；其次，提供精确的语言来传达回答这些问题所依赖的假定；再次，提供一种系统的方式以回答至少其中一些问题，并把其他的问题标记为“不可回答的”；最后，提供一种方法来决定，为了回答“不可回答的”问题，需要什么假定或者新的度量。限于篇幅，笔者只讨论了第一个问题，并没有具体阐述因果模型理论的成果（即后三个问题），观念固然重要，但是围绕着这个观念发展出一种理论以处理方方面面的问题更是需要经年累月的努力才行（当然还有历史的机运），且更多时候，当奔到终点，初始的想法早已面目全非。

再次，因果语言和概率语言的区分（即干预与观测区分的区分）也给决策理论（decision theory）的研究很多启发，之前的决策理论研究并没有清晰地区分行动和行为（对应着我们讨论中的干预与观测），比如，杰弗里（Jeffrey）[15]就把行动看作是寻常的事件，于是纯粹通过条件化来得到行动的效应，而这将会得到很多显然的悖谬性结论：“病人应该尽可能避免去看医生，‘以减少得重病的概率’；工人也不要急匆匆赶着去上班，以减少他们睡过了头的概率；学生们也不要为考试做准备，否则将证明他们之前没有努力学习，等等（珀尔）”[5]108-109，[16]130。而这种区分能够有力地廓清上述悖谬。

另外，与通过概率来理解因果的思路相对应，在哲学里面也有一种概率的因果理论，即试图通过概率来理解因果，即这是一种认为概率是一种更为根本的语言，并在此基础上来定义因果的理论。我们说X是Y的原因，是因为X的发生提高了Y发生的概率。这在直觉上似乎是完全可以接受的，正如我们说吸烟是得肺癌的原因，并不是说吸烟一定会得肺癌，而是说吸烟提高了得肺癌的概率。珀尔指出概率并不足以胜任作为因果的语言，“因果关系不能简化为概率”，在珀尔[5]249和珀尔和麦肯齐[2]23-51中指出正是哲学家们不假思索地诉诸这种处理不确定性的概率语言，而导致了数十年失败的探索。