螺旋给料机叶片分析及其厚度对挠度影响的模拟验证
李 勇 李忠毅 董 放
青岛科技大学机电工程学院 青岛 266061
0 引言
螺旋给料机是一种常见的连续散体物料输送设备,在实际生产过程中能实现变频调速并准确地控制输送量,主要用于中短距离的物料输送,现已广泛应用于各个行业[1]。但在实际生产应用中常常出现输送效率不高、输送误差大等问题[2],极大地影响了正常生产的需求。对此,国内很多学者针对不同结构参数的螺旋给料机进行了大量的研究。大连理工大学的张东海[3]利用遗传优化算法建立了参数化的螺旋给料机数学模型,计算、分析了螺旋叶片、螺距、螺旋轴等螺旋给料设备的关键部位,提出物料输送的影响因素有填充系数和螺距;杨乐成等[4]通过EDEM 建立垂直螺旋输送机输送物料的仿真过程,对叶片磨损情况进行了分析,得到了叶片磨损规律分析叶片磨损机理。周佳妮[5]提出随着螺旋转速的增大,螺旋叶片的磨损情况也随之加重。宁延州等[6]使用EDEM 软件对螺旋输送机关键部件(螺旋体)的轴径、螺距和叶片形状为变量进行仿真,得出影响水平螺旋输送机输送能力的关键因素是螺距、叶片和轴径的结论。本文就螺旋叶片的参数确定及其厚度的影响进行分析研究,为螺旋给料机的问题解决提供参考。
1 螺旋叶片分析
1.1 按螺旋线展开计算
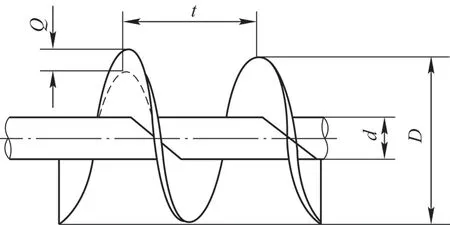
图1 螺旋叶片

图2 叶片的螺旋线展开图
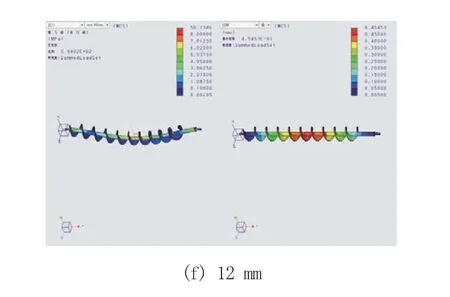
将图1 的螺旋叶片按精确螺旋线展开得到图2,根据图中各量的位置关系,可得外螺旋线L、内螺旋线l、叶片宽度b 和0 式中:L 为外螺旋线长度;t 为螺距;D 为螺旋叶片直径。L 为内螺旋线长度。D 为无缝钢管直径。 因R/r = L/l、R = b+r,可得r = bl/(L-l )。 将R'= R-Q 和L''=L 和代入,得 经过数学分析推导得 从式(6)可知,在d、D 和t 已经确定的情况下,ΔL 是Q 的函数,即ΔL=f(Q),可用数学方法求出ΔLmax和对应的Q。通过改变t(或D、b、d)来改变ΔLmax。但得到了ΔLmax并不能说明找到的相应位置是螺旋弯曲变形最大处,产生变形最大处在ΔL/L'最大值对应的叶片径向位置上[7]。 图3 螺旋叶片平面近似展开图 图4 几何证明 根据正弦定理 由此可知,α 的值决定了(ΔL/L')max,且取最大值时α=β。同时给定(ΔL/L')max的值,α 值也确定了[8]。 通过以上分析计算,得知如何合理选择叶片尺寸:调整t、d、D 的值,使(ΔL/L')max最小。 计算验证法在设计时先定下t、d、D,然后通过图4 的展开图,根据几何关系求出(ΔL/L')max时的α 值(α=β),再把α 代入式中,算出(ΔL/L')max,验证是否符合设计要求。 实例参数与螺旋计算结果如表1~表3 所示。 表1 实例参数 表2 1 号螺旋计算结果 表3 2 号螺旋计算结果 根据设计经验和理论计算,在设计时一般中等尺寸的螺旋叶片可取(ΔL/L')max=1%~4%,因此可得1 号螺旋体和2 号螺旋体叶片尺寸符合参数标准。 螺旋轴的挠度计算常采用材料力学的方法,即只计算螺旋轴本身的刚度,而忽略了螺旋叶片对螺旋轴挠度的影响,这种计算方法与实际挠度值相比有很大误差。 螺旋轴的挠度率为Ymax/L。根据刚度条件,许用挠度率一般为0.000 3~0.000 5,如按照Ymax/L=0.003~0.005和弹性模量E=200 GPa,可得空心螺旋轴径和需要跨度为 式中:L 为空心轴跨度,即轴两支撑之间的距离;q 为均布载荷集度;α 为空心轴的内外径之比,α=(d-2δ)/d。 式中:qd为管轴的均布载荷集度;qy为螺旋叶片的均布载荷集度,与螺旋叶片形式、外径和叶片厚度有关,此项不可忽视,会影响挠曲率的计算。精确计算需按照螺旋外径、螺旋面展开后算出;E 为弹性模量,与钢管材料和使用温度有关。表4、表5 为在下列温度下的弹性模量。 由表4 和表5 可知,通过改变钢管材料,增加弹性模量来降低挠度的方法非常有限,但钢材价格差异较大。由实例各项参数(表6)可以计算出,两端支撑螺旋轴的最大挠度。 表4 常见材料的弹性模量1 表5 常见材料的弹性模量2 表6 实例参数 螺旋轴最大挠度值计算公式为 式中: Ymax为螺旋体最大挠度;E 为钢管材料弹性模量,E=2.06×105MPa。 代入数据,得出1 号螺旋的最大挠度值Ymax=1.15 mm。同理得2 号螺旋Ymax=3.58 mm 。整理上述数据得到表7。 表7 挠度值 螺旋叶片对结构抗弯刚度的加强作用非常小,可以忽略不计,但它的质量影响螺旋轴挠度,故螺旋叶片厚度不宜太厚,但螺旋叶片可使扭转刚度增强20%。 螺旋体由无缝钢管制成的螺旋轴上焊接螺旋叶片制成,按照设计要求,工作时螺旋最大弯曲挠度不得超过5 mm,即螺旋外径与槽体内壁间距要小于5 mm[9]。 目前对于叶片对螺旋的影响,仅把质量作均布载荷加到螺旋轴上,而没有研究叶片对抗弯刚度的加强作用。无轴螺旋的出现说明叶片本身有一定的抗弯刚度。对于炭黑给料机螺旋叶片形状的选取,国内厂家大多数都是使用直线型单螺旋叶片,这种叶片形状加工制造简单,表面相对光滑,适合输送松散型物料[10]。国外炭黑输送行业出现了使用折线型叶片输送[11],故比较这两种类型叶片对螺旋轴挠度的影响。 1)模型建立 炭黑螺旋给料机整体零件较多,结构较为复杂,考虑到模拟分析过程的重点,在不影响模拟验证的前提下进行简化。本次模拟重点是分析叶片厚度和形状对螺旋轴挠度的影响,因此对于螺旋轴模型的建立,忽略中间悬架机构,只需将影响螺旋轴挠度的部分分析即可,因而模型由螺旋叶片、无缝钢管和轴端三部分组成[12]。 表8 螺旋体尺寸 mm 在Creo 界面建立模型,如图5 所示。依次对螺旋叶片厚度为2 mm、4 mm、6 mm、8 mm、 10 mm 以及12 mm,叶片形状变化的螺旋体进行模拟分析,得出模拟结果。 2)定义材料 首先定义模型的材料属性。螺旋轴的材料为45 号钢,在选择材料属性界面,选择标准中碳钢。工具栏材料分配里,选择整体模型分配为标准中碳钢。因为本次模拟的变量为叶片厚度,因此选择材料时,各定义量须保持一致。 3)施加约束 定义旋转约束时,选择两端销,约束只有X 轴方向的旋转,没有位移。定义整体约束可以选择销最右端的平面,固定XYZ 方向的位移。 4)施加载荷 螺旋轴在运行时主要受到重力和螺旋轴自转的离心力,这两个力都会影响到螺旋轴的挠度。选择转速为1 450 r/min 的电机,减速比为25.07,螺旋转速为57.8 r/min。施加重力载荷,全局设置重力加速度g =9.8 m/s2。施加离心力载荷,选择r/min 单位的转速,数值为57.8 r/min,方向为X 轴方向。 5)分析结果 选择测量参数为应力应变,进行静态分析,得出结果后查看有限元分析结果,得到应力及位移图。本次模拟比较的是叶片厚度变化对螺旋轴挠度的影响,因此需要用到应力图和位移变化量,在应力图中选择Von mises 应力;由于螺旋体的挠度是指在变形时其轴线上各点在该点处轴线法平面内的位移量,所以位移图可以显示该螺旋轴的挠度。 Von.Mises(冯米塞斯)准则指的是材料单位体积的变形超过一定的限度导致了材料到达了断裂或屈服的状态,导致材料变形的限度就是单向拉伸(或压缩)到达危险状态(断裂或屈服)的单位体积变形能。冯米塞斯应力是一种根据第四强度理论得到的当量应力,考虑了第一、二、三主应力,可以用于对疲劳、破坏等的评价。 如图6 所示,通过Creo simulate 的分析功能,模拟出了叶片厚度分别为2 mm、4 mm、6 mm、8 mm、10 mm 以及12 mm 时螺旋体的应力和变形量图。在叶片厚度为2 mm、4 mm、6 mm、8 mm、10 mm、12 mm 时螺旋体中间部分的冯米斯应力最大值分别为2.9 MPa、3.8 MPa、4.5 MPa、5 MPa、6 MPa、7.1 MPa,最大位移均出现在螺旋轴中间部分,最大变形量分别为0.164 mm、0.226 mm、0.286 mm、0.343 mm、0.399 mm、0.454 mm。在无缝钢管尺寸、轴端尺寸、叶片直径、螺旋叶片长度不变的情况下,螺旋叶片厚度由2 mm 变化到12 mm,导致螺旋体中间部分的冯米斯应力最大值由2.9 MPa 变化到7.1 MPa,最大位移都出现在螺旋轴的中间部分,最大变形量由0.164 mm 变化到0.454 mm。 图5 螺旋体模型 图6 不同叶片厚度螺旋体应力及形变 应力和变形量随叶片厚度变化如图7、图8 所示,可直观地了解螺旋轴所受的应力及螺旋体中间部位的最大变形量随叶片厚度的变化趋势。螺旋轴叶片厚度在2~12 mm 内变化时,其所受冯米塞斯应力近似呈线性增长,没有骤增的趋势。同样,螺旋轴中间部分的最大变形量也近似呈线性增长,没有骤增的趋势。 图7 应力随叶片厚度变化图 图8 变形量随叶片厚度变化图 折线型螺旋叶片指的是母线形状为折线的螺旋叶片,其优点是可以节省材料,减轻螺旋轴质量,在国外应用较广。为保证螺旋叶片根部的结构强度,设定叶片根部厚度为4 mm,叶片外轮廓厚度为6 mm,根部和外轮廓轴向尺寸相等,截面如图9 所示。其他尺寸不变,生成模型(如图10)。 图9 叶片截面图 图10 模型细节图 对于分析折线型叶片与普通叶片对螺旋轴挠度的影响,其模拟过程与普通叶片模拟过程相同,除叶片形状外,材料属性、约束载荷、测量数据等保持不变。 图11 不同厚度折线型叶片螺旋体应力及形变 通过图11a 模拟结果可得,叶片根部厚度为4 mm、外轮廓厚度为6 mm 的折线型叶片螺旋体中间部分的冯米塞斯应力最大值约为4.1 MPa,最大位移仍然出现在螺旋轴中间部分,最大变形量为0.264 mm。相比较于叶片厚度为6 mm 的螺旋体,其大小约为4.5 MPa,最大变形量为0.286 mm,其冯米塞斯应力和形变量略微降低。为得到准确结论,需要再分析一组叶片根部厚度为5 mm,叶片外轮廓厚度为8 mm 的折线型叶片与厚度为8 mm 的普通叶片的模拟数据。 通过图11b 模拟结果可知,叶片根部厚度为5 mm、叶片外轮廓厚度为8 mm 的折线型叶片螺旋体中间部分的冯米赛斯应力最大值约为4.7 MPa,最大位移仍然出现在螺旋轴中间部分,最大变形量为0.313 mm。相比较于叶片厚度为8 mm 的螺旋体,其大小约为5 MPa,最大变形量为0.343 mm,其冯米塞斯应力和形变量略微降低。 综合两组数据可知,减小叶片根部厚度,螺旋轴的冯米塞斯应力和形变量也会减小,但是幅度很小。推测导致冯米塞斯应力和形变量减小的原因可能是叶片根部厚度减小,螺旋体总重减小,导致的螺旋体挠度小幅增大。 在实际生产中,螺旋体的挠度会受如涂层、焊接工艺、材料处理、输送物料属性等其他因素的影响,但是这些因素在相同的条件下,仅仅由叶片厚度变化导致的螺旋轴挠度变化不大,且螺旋叶片厚度增大导致的抗弯模量增加影响小于叶片厚度增大导致的质量增大对螺旋轴挠度的影响。因此在设计螺旋叶片时,应注意螺旋叶片的厚度不宜过大,在保证螺旋叶片强度的前提下,应尽量减小叶片厚度,节省材料的同时,可略微降低螺旋轴的挠度。同时可酌情减小螺旋叶片根部厚度,虽然对主轴挠度影响较小,但会对加工难度造成影响,应综合考虑。同时,本模拟也证明了工程上螺旋设计挠度计算将螺旋叶片质量分布在螺旋轴上、叶片对螺旋轴的抗弯模量没有影响的这种设计方法是正确的。





1.2 实例验证计算



2 最大挠度计算
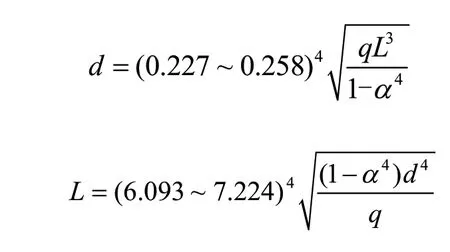
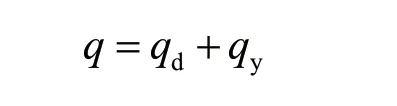





3 叶片厚度对挠度的影响模拟验证
3.1 直线型螺旋叶片





3.2 折线型螺旋叶片


4 结论

