基于GMDH与dce-GMDH算法的上市公司财务危机预测研究

石 峰，胡 燕

(1.湖南工程学院 管理学院，湖南 湘潭 411104；2.中南大学 法学院，湖南 长沙 410012)

对于投资者和其他利益相关者而言，预测上市公司的上市状态至关重要。在我国证券市场，特别处理的股票除了涨跌幅度受到限制以外，其股票名称之前还须注释为“ST”。如果该ST企业仍然持续亏损，将面临被退市的风险。现有研究倾向于应用二进制分类将上市状态分为ST和非ST两类，以便于计量。国外关于上市公司的财务危机预测研究，主要运用支持向量机、决策树、判别分析、神经网络等二进制分类模型进行。国内针对上市公司的财务危机预测研究，主要运用判别分析、逻辑回归、聚类分析和生存分析等传统的分类预测方法。然而这些预测方法通常需要做出假设，例如逻辑回归中要求logit(p)和自变量之间存在线性关系；判别分析中要求各变量相互独立，且服从多元正态分布。因此，当自变量的数量逐渐增多且高度相关时，这些预测方法的估计结果往往会出现偏误。另外，已有研究在指标选择上，主要选取偿债能力、营运能力、盈利能力、成长能力、现金流量和资产结构等方面的少量财务指标，具有一定主观性。

分组数据处理方法(Group Method of Data Handing， GMDH)型神经网络算法是用于对复杂系统进行建模的自组织算法，多种分类集合的GMDH(dce-GMDH)算法是集支持向量机(svm)、随机森林(rf)、朴素贝叶斯(nb)、弹性网逻辑回归(en)、神经网络(nn)等分类器为一体的GMDH算法，二者被广泛应用于回归、分类、聚类和预测等研究领域。与以往应用于上市公司财务危机预测的方法相比，GMDH算法和dce-GMDH算法没有严格的假设限制。由此，本文首次将GMDH算法和dce-GMDH算法应用于我国沪深A股上市公司的财务危机预测中，构建全面反映盈利能力、经营增长、资产质量和债务风险等4个维度的17个财务指标的GMDH和dce-GMDH算法财务危机预测模型，并评价与比较二者的预测性能。

一、GMDH与dce-GMDH算法

(一)GDMH算法的基本原理

IVAKHNENKO为更好地预测河流中的鱼类种群，创造了分组数据处理方法(GMDH)，使神经元成为具有多项式传递函数的更复杂的单元，并简化了神经元之间的互连，同时开发了用于结构设计和权重调整的自动算法[1]。IVAKHNENKO构造的多项式为：

(1)

其中,m表示每个神经元进入回归模型的变量数量；a,b,c…是多项式中变量的权重。y是响应变量；xi和xj是探索性变量。在本研究中，上述模型仅包含主要影响，由此可表示为：

(2)

若上式(2)为二变量多项式，则将构造m*(m-1)/2个候选神经元，其中m是上一层中的神经元数量。如果选择以允许来自上一层和输入层的输入，则m将是上一层和输入层中神经元数量的总和。如果选择以允许来自任何层的输入，则m将是输入变量的数量加上所有先前层中的神经元数量的总和。

在模型建立和评估过程中，数据被分为三组：训练集(60%)、验证集(20%)和测试集(20%)。训练集包含在模型构建中,验证集被用于对神经元的选择；测试集被用于考察评估模型在未观察数据上的性能。GMDH算法是由神经元构成的层次系统，其每层中神经元的数量取决于输入的数量。假设进入某一个层的输入数量等于p，则该层中的神经元数量变为：

(3)

上式(3)考虑了所有成对的输入组合，但这并不意味着所有层都包括h个神经元。例如，输入层中的输入数量仅定义第1层中的神经元数量。在第1层中选择的神经元数量决定第2层的神经元数量。该算法自行组织架构，当存在3个层次和4个输入时，GMDH算法的体系结构如图1所示。

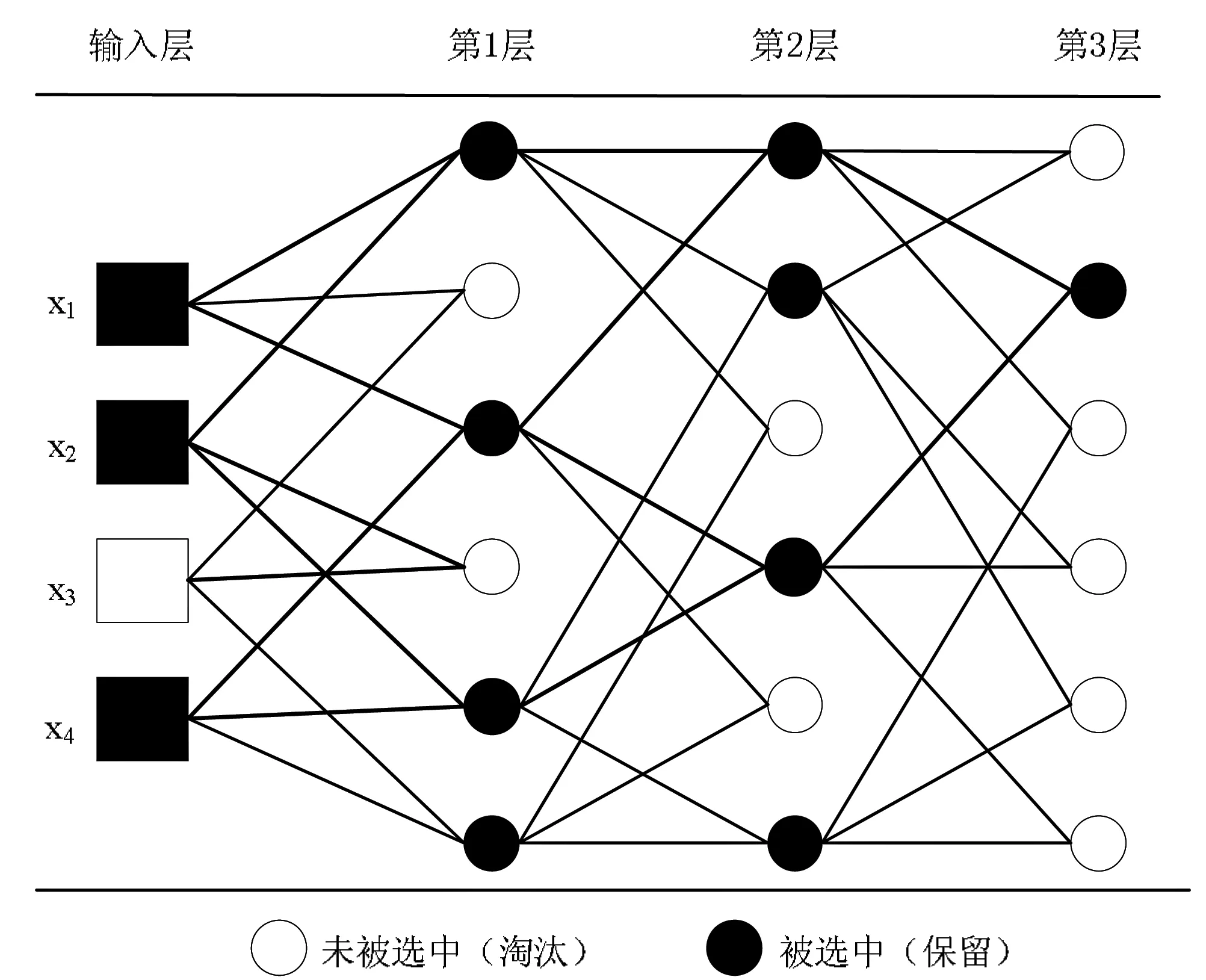
图1 GMDH算法的体系结构

在图1的GMDH算法体系结构中，存在4个输入(x1,x2,x3,x4)，其中3个变量(x1,x2,x4)主导着系统，而x3对分类没有影响。GMDH算法会自组织选择对分类有影响的输入变量，这说明网络中神经元之间的连接不是固定的，而是在训练期间进行选择以优化网络；网络中的层数也会自动选择，以产生最大的精度而不会过度拟合。

(二)GDMH算法的基本流程

GMDH算法的基本流程有以下几个步骤：①构造仅显示每个输入预测变量值的第一层。②使用允许的函数集，使用上一层输入的组合来构造所有可能的函数。③使用最小二乘回归计算每个候选神经元中函数的最佳参数，以使其最适合训练数据。如果选择了非线性函数(例如逻辑或渐近函数)，则使用基于Levenberg-Marquardt方法(LM算法)的非线性拟合。④通过将其应用于训练数据来计算每个神经元的均方误差。⑤按均方误差增加的顺序对候选神经元进行排序。⑥从候选神经元中为下一层选择最佳(均方误差最小)神经元；模型构建参数指定每层中使用了多少个神经元。⑦如果使用训练数据测得的层中最佳神经元的均方误差比前一层中最佳神经元的均方误差好，并且尚未达到最大层数，则跳回到步骤②以构造下一层。否则，停止训练。需要注意的是，当过度拟合开始时，使用训练数据测得的均方误差将提高，从而停止训练。

(三)基于多种分类器集合的dce-GMDH算法

多种分类集合的dce-GMDH(diverse classifiers ensemble based on GMDH)算法是集支持向量机(svm)、随机森林(rf)、朴素贝叶斯(nb)、弹性网逻辑回归(en)、神经网络(nn)等分类器为一体的GMDH算法。与GMDH算法不同，dce-GMDH算法不仅包括基础层，而且将分类器放置在基础层，从而使用通过这些分类器的所有输入来获得预测概率。与此同时将分类器获得的预测概率继续作为第1层的输入，而无须应用任何神经元作为选择过程,其余算法与GMDH算法相同。dce-GMDH算法的体系结构如图2所示。

由图2看出，dce-GMDH算法的体系结构是由输入层、基础层、第1层、第2层和第3层构成的分层系统。输入层存在4个输入(x1,x2,x3,x4)，并从基础层进入到每个神经元。基础层包括5个分类器，即基础层中的神经元数量为5个，其它层的神经元数量由输入的数量决定。该算法通过自组织方法来选择最合适的分类器。在基础层的每个神经元中存在一个不同的分类器，通过分类器利用四个输入获得预测概率。基础层中的5个输入进入到第1层，因此第1层神经元数量为10，根据外部标准，保留了4个神经元，并从网络中淘汰了6个神经元。由于在第1层中选择了4个神经元，因此第2层中的神经元数量变为 6。该过程一直持续到实现停止规则为止。

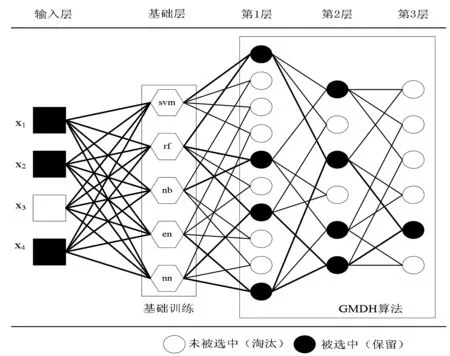
图2 dce-GMDH算法的体系结构

二、实证分析

(一)数据来源与预测变量

本文实证数据来源于巨潮资讯网公布的沪深A股上市公司2019年第4季度的财务指标数据。截止到2019年12月31日，深市A股上市公司2 179家，沪市A股上市公司1 488家，沪深A股上市公司共计3 667家，其中88家是“*ST”公司，52家是ST公司。根据我国大多学者关于公司是否处于财务危机的界定，以该公司是否连续两年亏损和被特别处理进行判断。因此，无论经营连续两年亏损、被特别处理(即“ST”)的公司，还是经营连续三年亏损、被退市预警(即“*ST”)的公司，本文都归类为ST公司，共计140家。

本文进一步对数据进行筛选，以满足GMDH算法和dce-GMDH算法对数据的要求。在140家ST公司中，删除财务指标有缺失数据或为0的两家ST公司，为避免样本不均衡导致的多数类更容易被判断正确，以1︰1配对原则在沪深A股上市公司中随机选取138家非ST公司，由此得到17个财务指标的138家ST公司和138家非ST公司样本组。

本文的研究目的是运用GMDH与dce-GMDH算法对我国沪深A股上市公司是否处于财务危机做出正确预测分类。因此，本文在选取财务指标构建财务危机预测模型时，参考了2006年国务院国资委发布且一直沿用至今的《企业综合绩效评价实施细则》所规定的财务绩效评价指标体系。该财务绩效评价指标体系包括8个基本指标和14个修正指标，共计22个评价指标，且分别隶属于盈利能力、经营增长、资产质量和债务风险等4个维度，能较为全面地评价我国上市公司的财务绩效状况。

由于部分财务指标数据缺失，本文选取了净资产收益率(x1)、资本收益率(x2)、总资产报酬率(x3)、营业利润率(x4)、成本费用利润率(x5)、盈余现金保障倍数(x6)、总资产增长率(x7)、营业收入增长率(x8)、营业利润增长率(x9)、净利润增长率(x10)、总资产周转率(x11)、流动资产周转率(x12)、总资产周转天数(x13)、流动资产周转天数(x14)、资产负债率(x15)、速动比率(x16)、流动负债比率(x17)等17个财务指标作为我国沪深A股上市公司财务危机预测模型的预测变量(见图3)。

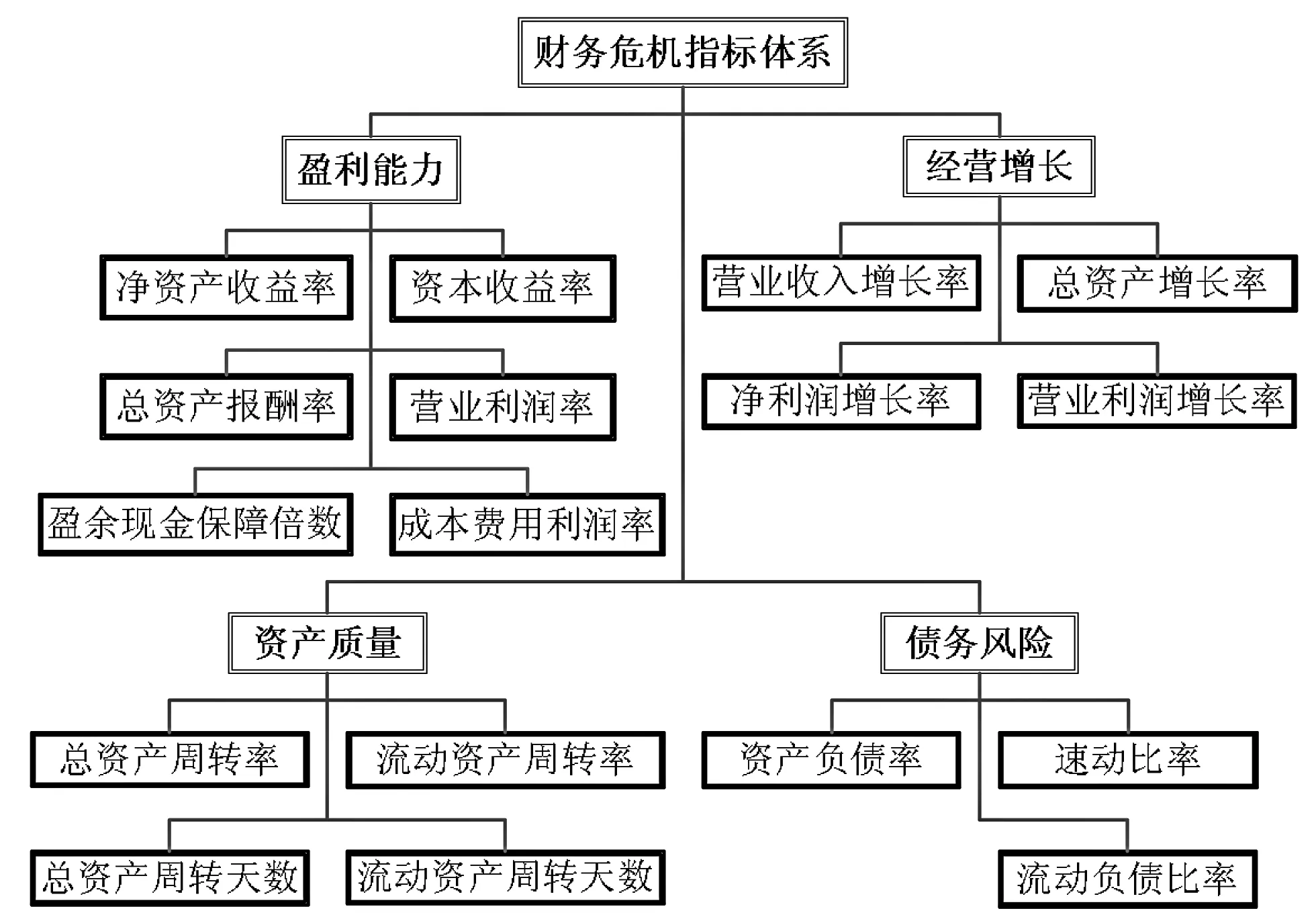
图3 沪深A股上市公司财务危机预测指标体系

(二)基于GMDH算法的特征选择与分类预测

二进制分类可以将二进制目标标签分配给每个观察值,从而通过分组数据处理(GMDH)算法对两标签输出进行分类。GMDH算法适用于复杂的非结构化系统，并且比高阶回归具有优势。通过GMDH型神经网络算法执行二进制分类存在两种主要算法：GMDH算法和基于各种分类器集合的GMDH(dce-GMDH)算法。

本文参考OSMAN和YOZGALTIGIL开发的R语言GMDH函数对我国沪深A股上市公司的财务指标进行特征选择[2]，同时使用OSMAN和ERDEM最新开发的 GMDH2函数进行财务危机分类预测[3]。

首先，本文将数据随机分为训练集、验证集和测试集，然后调用GMDH函数。此函数中的第一个和第二个参数分别是探索变量的矩阵和训练集中的一个因子；第三和第四个参数分别是探索变量的矩阵和验证集中的一个因子。alpha参数是选择压力。maxlayers参数是指定的最大图层数。maxneurons参数是第二层及后续层中允许的最大神经元数量。exCriterion参数是用于神经元选择的外部标准。

运行GMDH函数得到的结果如表1所示。由表1看到，我国上市公司财务危机分类预测的算法结构包括层、神经元、被选中神经元和最小均方误差。该算法结构共计2层，每层神经元的数量分别为136和105；第1层和第2层被选中的神经元分别为15和1。计算神经元的外部标准为最小均方误差，每层对应的最小均方误差分别为0.135 9和0.134 7。

表1 上市公司财务危机预测的算法结构输出结果

图4为GMDH算法在每个相应层的验证集上给出的最小外部标准值(均方误差)。当层数为2时，最小均方误差达到最小值0.134 7。根据GMDH算法的体系结构，GMDH算法会自组织选择对分类有影响的输入变量，该算法从17个变量中选择了4个变量(x1,x3,x4,x7)，即净资产收益率、总资产报酬率、营业利润率和总资产增长率。

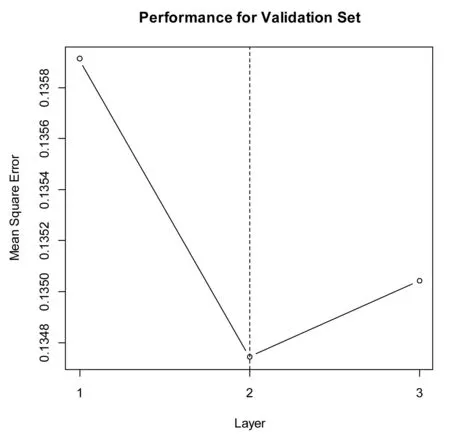
图4 GMDH算法每个相应层的最小均方误差

在模型构建完成后对测试集进行预测。测试集共有55个观测值，预测结果如表2所示。从表2看出，GMDH算法预测第1家公司为“ST”和“非ST”的概率分别为0.93和0.07，由于第1家公司为“ST”的概率大于为“非ST”的概率，因此第1家公司归类为ST公司。在55个测试样本中，归类为ST公司的有1、2、3、4、5、6、9、10、11、12、13、14、17、18、19、21、22、23、25、26、27、28、29、30、32、50和55；其它公司归类为非ST公司。

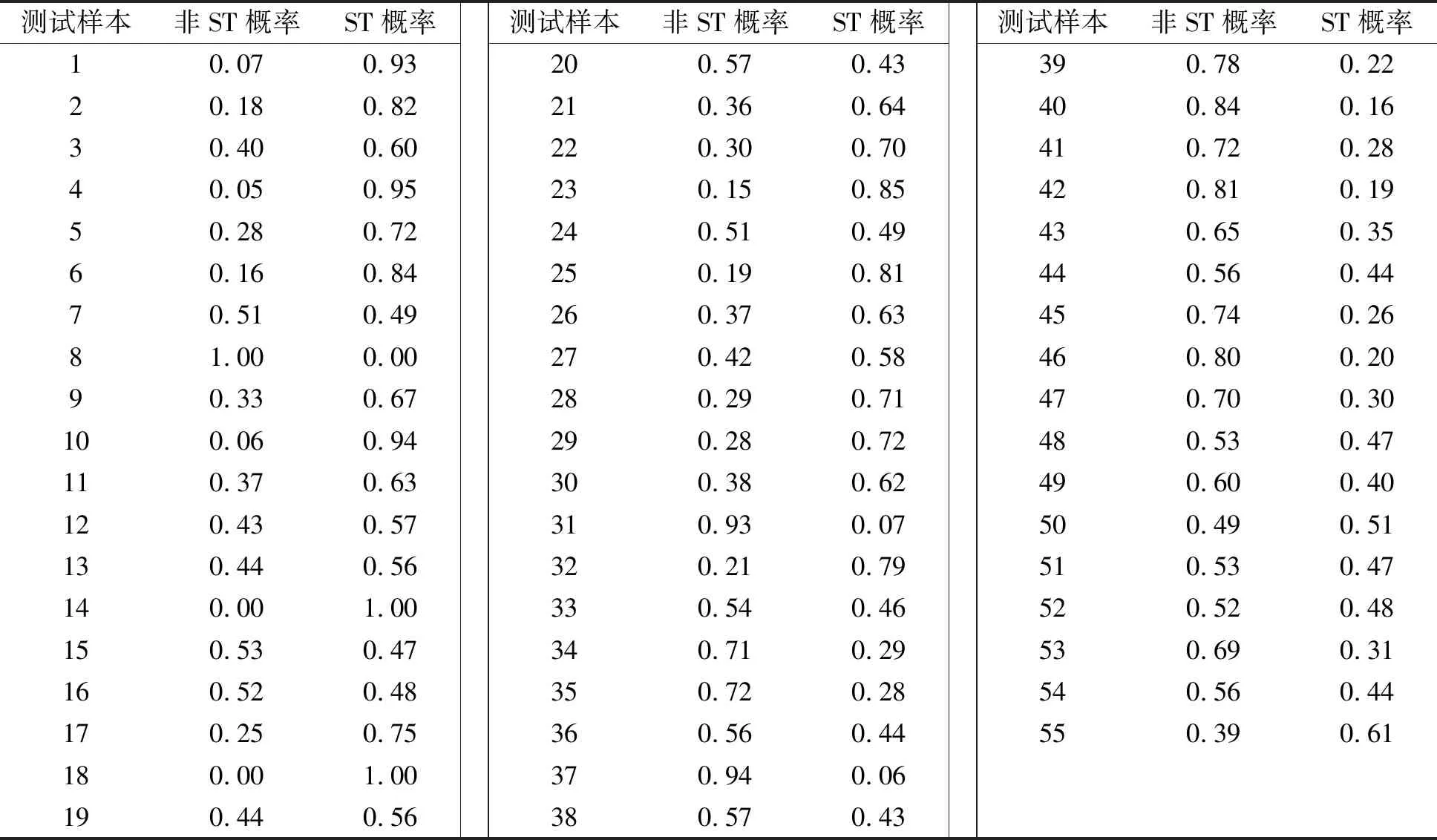
表2 测试集的分类预测结果

随后，利用R软件中的confMat函数为二进制响应生成一个混淆矩阵，并得到预测正确率、敏感性值和特异性值等统计信息。GMDH算法的分类预测正确率为0.836 4。这说明该算法将83.64%的公司分类为正确的类别，即55家公司中有46家公司分类正确，其中25家ST公司分类正确，2家ST公司分类错误；21家非ST公司分类正确，7家非ST公司分类错误。与此同时，由confMat函数计算出的敏感性值和特异性值分别为0.781 2和0.913 0。这表明该算法将78.12%的ST公司和90.13%的非ST公司正确分类，即在分类预测结果中，32家ST公司有25家ST公司分类正确；23家非ST公司有21家非ST公司分类正确。

本文以变量x1和x3为分类标签绘制出二维散点图和以变量x1、x3和x7为分类标签绘制出三维散点图(见图5和图6)。图5和图6中的“FALSE”表示分类错误，“TRUE”表示分类正确；“nst”表示为“非ST”公司，“st”表示为“ST”公司。无论是从图5的二维散点图，还是从图6的三维散点图都能发现：有2家“ST”公司被错误分类成“非ST”公司；有7家“非ST”公司被错误分类成“ST”公司。

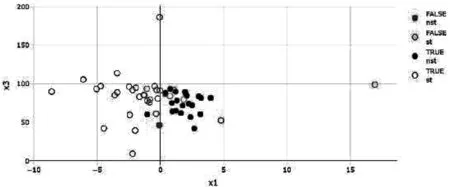
图5 分类标签二维散点图

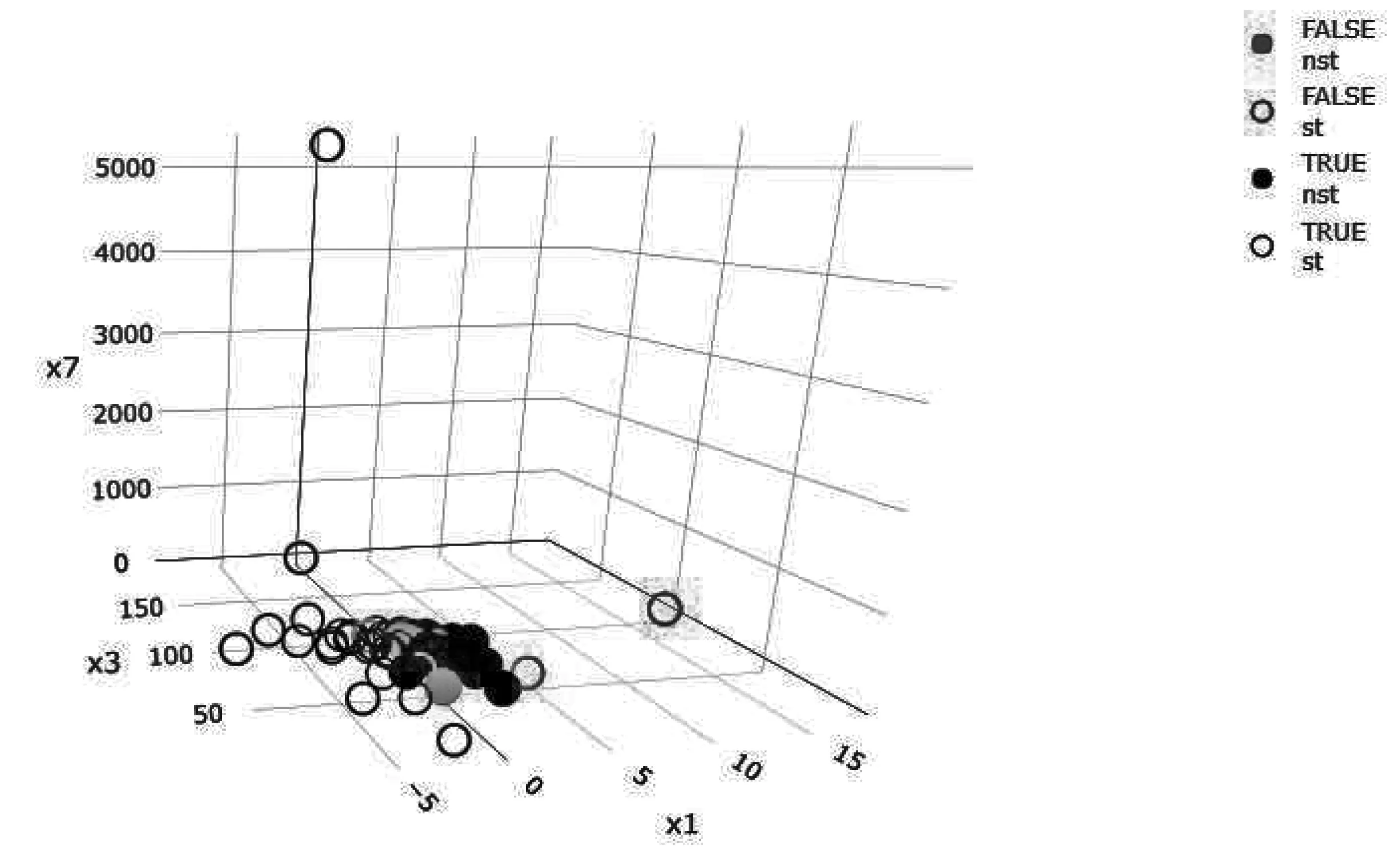
图6 分类标签三维散点图

(三)基于dce-GMDH算法的分类预测

dce-GMDH函数中的alpha参数是选择压力，maxlayers参数是指定的最大层数，maxneurons参数是第二层及后续层中允许的最大神经元数量，exCriterion参数是用于神经元选择的外部标准。dce-GMDH算法是组合了分类器的GMDH算法，因此，dce-GMDH函数用于分类器选项的参数主要有svm_options、randomForest_options、naiveBayes_options、cv.glmnet_options和nnet_options等。

图7为dce-GMDH算法在每个相应层的验证集上给出的最小外部标准值(均方误差)。当层数为1时，最小均方误差达到最小值0.115 2。我国沪深A股上市公司财务危机预测的dce-GMDH算法是将两个分类器(随机森林和神经网络)组合在一起的集成算法。

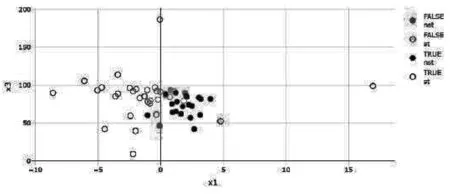
图7 dce-GMDH算法每个相应层的最小均方误差

随后，对测试集的55个观察值进行预测。dce-GMDH算法将测试集中的1、2、3、4、5、6、8、9、10、11、12、13、14、16、17、18、19、21、23、24、25、26、27、28、29、30、32、38、50、55等公司归类为ST公司，其它为非ST公司。

dce-GMDH算法的分类预测准确率为0.854 5，即在55家公司中有47家公司分类正确。敏感性值和特异性值分别为0.875 0和0.826 1。这表明dce-GMDH算法将87.5%的ST公司和82.61%的非ST公司正确分类，即在分类预测结果中，32家ST公司有28家ST公司分类正确；23家非ST公司有19家非ST公司分类正确。从图8显示的以和为分类标签的二维散点图看到：32家ST公司中有4家ST公司分类错误；23家非ST公司中有4家非ST公司分类错误，预测准确率为85.45%。由此可见，与GMDH算法相比，使用dce-GMDH算法可将分类预测准确率提高约2%。

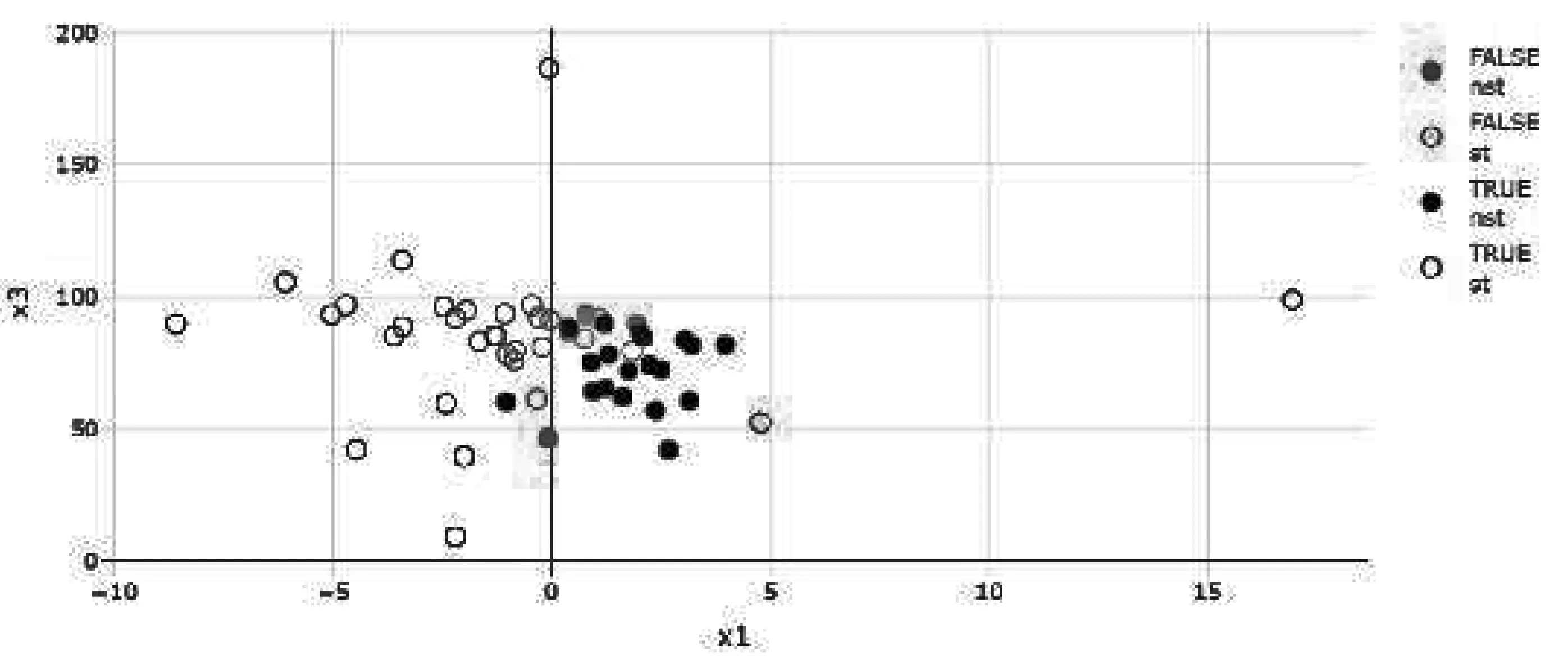
图8 dce-GMDH算法的分类标签二维散点图

三、结语

本文根据国资委发布的《企业综合绩效评价实施细则》所规定的财务绩效评价指标体系，构建了全面反映盈利能力、经营增长、资产质量和债务风险等4个维度的17个财务指标的GMDH和dce-GMDH算法财务危机预测模型。针对我国沪深A股上市公司的138家ST公司和138家非ST公司样本组，基于GMDH算法的预测准确率为83.64%，具有较高的预测精度。敏感性值和特异性值分别为0.781 2和0.913 0，即该算法将78.12%的ST公司和90.13%的非ST公司正确分类；基于dce-GMDH算法可将分类预测准确率提高约2%，达到85.45%。敏感性值和特异性值分别为0.875 0和0.826 1，即dce-GMDH算法将87.50%的ST公司和82.61%的非ST公司正确分类。

GMDH算法是借助生物控制论中的自组织原理而提出的一套建模方法。这一方法是启发式的，不是用解析式的方法进行推导，建模过程是自组织的，即自动进行变量组合、筛选以及判断是否得到合适的模型。MDH算法的主要特点是，以充分合理地利用数据，并用局部的简单的算法建立整体上复杂的模型。特别是在变量多、数据少、现有的其它建模方法很难胜任建模任务的情形下，GMDH算法却可以得到十分令人满意的结果。需要指出的是，GMDH算法和多种分类集合的GMDH(dce-GMDH)算法在ST与非ST公司两类公司中具有较高的分类预测效果，而并非这两种方法本身具有强较的预测能力。