基于区域推荐孪生网络的目标人员锁定与跟踪系统

蒋天翼

（杭州电子科技大学计算机学院 浙江省杭州市 310018）

1 引言

目标跟踪是近年来人工智能方向的热门领域，近年来其发展势头迅猛，并被广泛应用在安防系统、自动驾驶、体育赛事转播、公共交通等领域。在传统的单目标跟踪任务中，首先给定视频初始帧的目标位置，即目标在视频帧中的边界框，使用相关跟踪方法，输出后续视频帧中目标所在的位置信息以及宽高信息。然而在实际运用中，被跟踪物体往往会发生形变、高速运动、干扰物遮挡等问题，给目标跟踪任务带来了极大的挑战。因此，如何克服物体在运动中发生的变化，从而较为准确地跟踪目标，是该领域的一个关键问题。

2 相关工作

目前，许多目标跟踪算法都得到较成熟的发展。在被广泛运用于计算机视觉的各种方法中，均值漂移是一种常见的聚类算法，Comaniciu 等人首次将其与目标跟踪相结合，提出基于均值漂移的目标跟踪算法[2]。具体来说，这种方法无需先验知识，而仅需要先对待跟踪对象建模，在当前视频帧中不断迭代搜索框，使其沿着图像特征均值漂移方向不断移动，最终确定目标坐标。均值漂移方法迭代速度快，计算效率高，但健壮性较差，并且由于目标边界框大小固定，在目标发生大小形变时难以产生准确结果。另一方面，采用相关滤波来进行目标跟踪的方法也随之出现，并逐渐成为一种主流的跟踪手段。Bolme 等人提出的MOSSE 算法[3]，首次将信号处理与目标跟踪相融合。其算法目的是训练一种相关滤波器，使得被跟踪目标能在视频帧中得到最高的响应度。MOSSE 方法只需要图片的灰度特征，这进一步提高了算法的运行效率，跟踪速度可以超过几百帧每秒。在这之后也有许多优秀的相关滤波方法，如CSK[4]、KCF[5]等，其核心目标就是训练一个能够区分当前视频帧前景与背景的分类器。这种算法的执行速度通常较高，能够达到实时需求，但抗干扰能力依旧不是很理想。另外，由于相关滤波方法需要经常对滤波器进行更新，这对算法执行速度也产生一定影响。

自从近年以来，基于深度学习的方法在计算机视觉领域渐渐展露其非凡的实力。Alex Krizhevsky 等人提出的AlexNet[6]首次将卷积神经网络（CNN）用于目标分类任务，获得了十分理想的效果。CNN 网络有着强大的特征提取能力，能够更加准确的挖掘目标浅层和深层的语义信息，这对目标跟踪任务也适用。2015年由Ma等人提出的HCF 算法[7]，在KCF 算法的基础上，将深度学习中的CNN 网络与相关滤波的方法融合，用深度学习特征替代原有的HOG 特征，使跟踪器能够应对目标较大的位移变化，并有效防止跟踪器漂移。在深度学习的一系列方法之中，孪生网络借由其共享网络权重的特点，非常适合相似性度量的任务。SiamFC[8]算法通过将模板帧和跟踪帧经过CNN 提取后的特征进行互相关操作，得到目标位置的预测分数。Siamese-RPN[1]在其基础上进一步提出了区域举荐网络（Region Proposal Network），使得目标候选框的生成更加准确。但在大部分孪生网络的跟踪方法中，它们只能从非语义的背景中识别前景，而不好识别的背景就很容易被认为是干扰物。为了解决孪生网络难以识别干扰物的问题，本文提出了基于概率回归的方法模型，将其用在目标跟踪领域，有效提高了网络的抗干扰能力，在VOT2018 数据集上表现优秀。

3 基于孪生网络的神经网络结构

孪生网络是众多神经网络中较为特殊的一种，它由两个或以上子网络构成，同时可以接受两个以上的输入，并共享这几个网络分支的权值。孪生网络的核心思想是找到一组参数，使得目标空间的距离近似地等价于输入空间的“语义”距离，使得相似度度量在同类别中较小，不同类别中较大。

基于全连接层孪生网络框架的跟踪模型：

由于孪生网络结构非常适合相似性度量，事实上，早在2016年来自牛津的Luca Bertinetto 便基于此网络结构推出了基于全连接层孪生网络框架的跟踪模型——SiamFC[8]。算法的核心思想是通过训练一个函数f(z,x)来比较样本图像z 和待查询图像x 的相似性，如果是一致的目标则判定为分数较高，反之给予较低的分数。

图1描绘的是全连接孪生网络的架构。首先特征提取网络将对网络的两个输入z 和x 进行相同的变换φ，并且把得到的输出传递给互相关模块。相似性度量函数也可由此过程后得到：f(z,x)=g(φ(z),φ(x))。本文采取该架构，针对搜索到的图像x 进行全连接卷积操作，并输出含有标量值的分数图，同时以图像大小来决定尺寸。

这种跟踪模型选用视频上一帧中预测的目标中心位置作为当前帧的位置来进行搜索并跟踪。其中需要的最大的得分的位置，其值与得分图的中心有关。用这个值乘上方法中网络的步长，从而可以得到不同帧之间的目标的相对位移。在单次的操作中，以多种不同的尺度对目标进行搜索，进而得到合适的候选框。

4 基于概率回归的孪生网络目标跟踪方法

视觉目标跟踪的任务本质是将一个视频拆分为若干帧图片，并对每一帧图片预测目标状态的一种任务，其中最普通的情况就是使用矩形框来框选需要跟踪的目标范围。和别的机器视觉任务，如目标检测还有定位等类似，目标跟踪任务也可以看作一个回归任务。跟踪器算法需要去学习一个比较通用的模型，这种模型能够识别目标在每一帧中的位置和状态。传统的跟踪模型使用置信度回归作为优化方向，采用置信度预测值s(y,x)来描绘视频输入帧的特征x 与当前区域y 相似的可信度。完成这步之后，采用置信度分数y*=argmax{s(y,x)}，对所有y 来进行估计并最大化这个分数，从而得到这个条件下最好的结果。

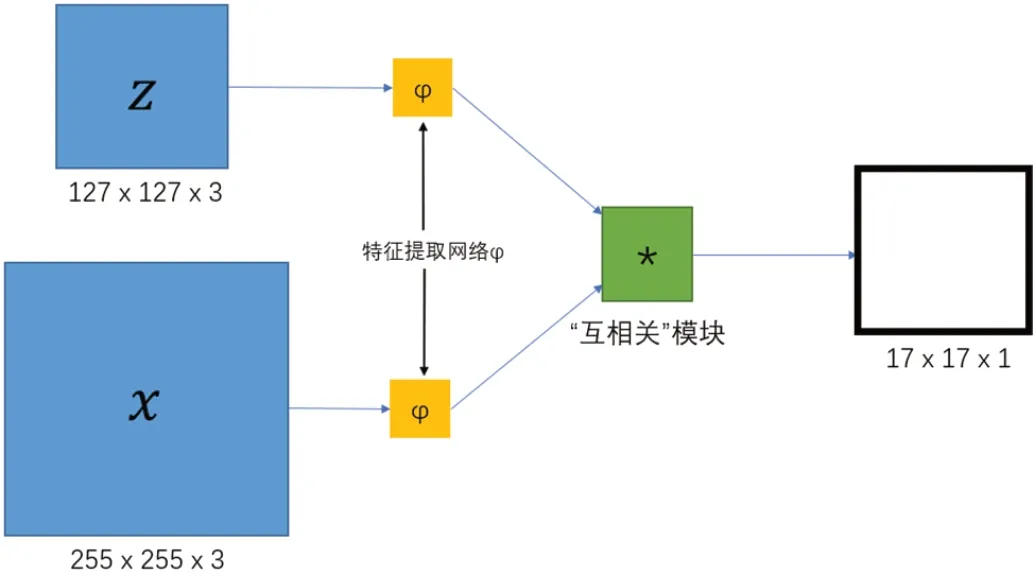
图1：全连接层孪生网络框架图

图2：目标框和目标中心对比

图3：经处理后的训练集图像

基于置信度回归的目标跟踪方法，主要用在主流跟踪算法，如相关滤波方法或基于深度学习的方法等之中。不同于在直接回归方法中采取y=f(x)来预测单个y，而忽略背景中的其他信息，基于置信度回归的方法在表达一些不确定的物体上非常灵活。但同时，在置信度回归中，所谓的置信度值并没有比较明确清晰的解释，仅仅是一个应当被最大化的目标分数而已，在解释为何产生分数会最大上面欠缺说服力。由于置信度值的范围和特性很依赖模型选择的损失函数和生成训练的伪标签，这令研究者难以设计出合适的估计方法，而在推理预测的过程中也会因这些原因而倍感压力。另外，在目标跟踪任务中，只要目标产生微小的变化，目标框中心位置和目标的中心位置就会有很大的不同，如图2所示。由于一般的回归方法只专注回归目标中心本身，而忽略了目标框中心和目标中心的差别，这对跟踪准确度来讲是一个不能忽视的挑战。

本文在Saimese 网络中使用概率回归目标框的方法替代置信度回归，使得上述问题得到解决。

4.1 基于概率回归方法

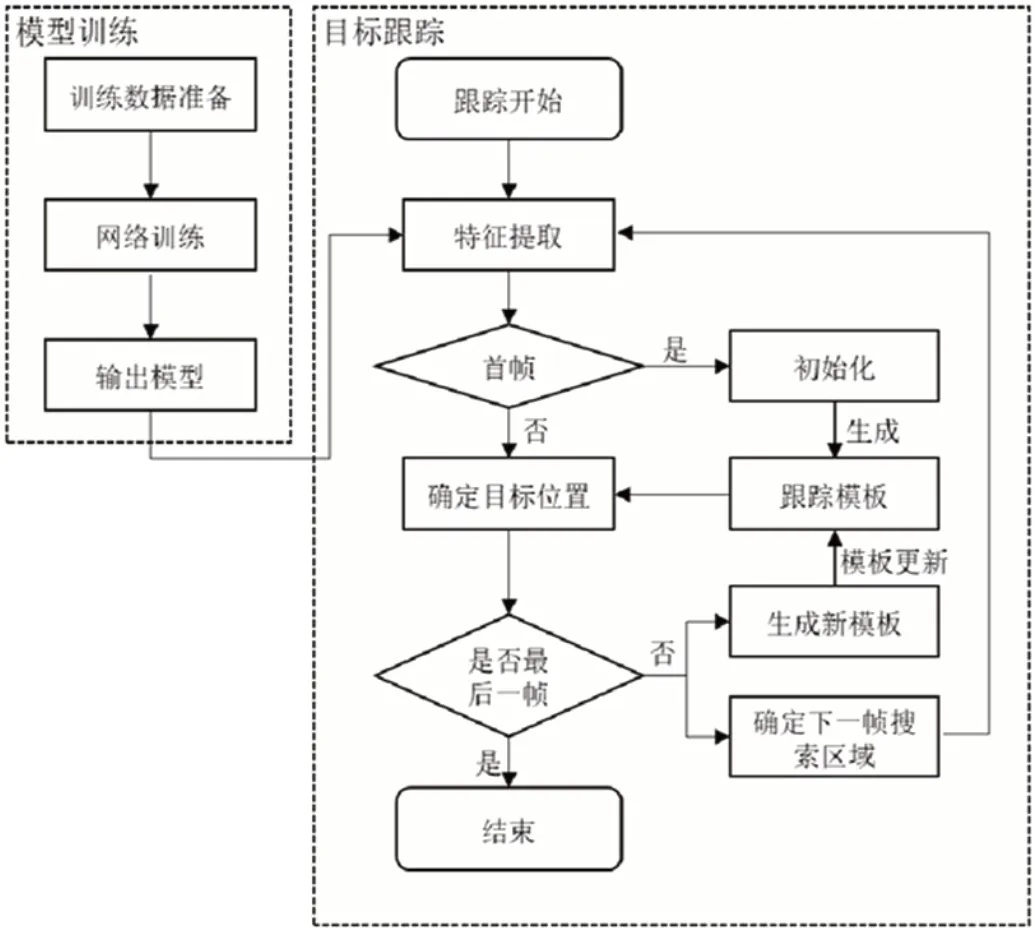
图4：目标跟踪算法流程框架图

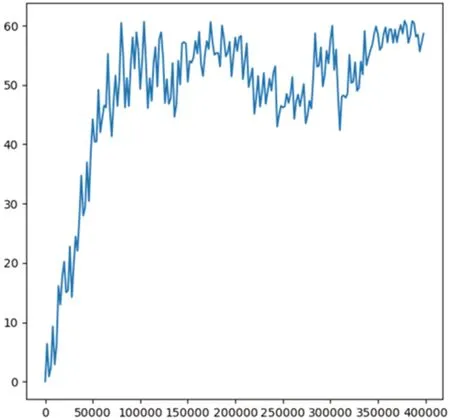
图5：准确率AUC 与迭代次数关系图

本文用概率回归替换置信度回归，并将其用于Siamese 网络框架之中。这种方法拥有大部分置信度回归方法的优点。但与其不同的是，本方法用预测的概率分布p(y|x,θ)，其中θ 是概率分布的参数。网络的优化方向是最小化预测概率分布p(y|x,θ)与条件真值的概率分布P(y|yi)之间的KL 散度。在测试中，选择概率密度最大的点作为预测结果，也就是目标中心点。

与普通的回归方法相比较，这种方法有如下几个特点。首先，在一般的回归方法中，预测值s(y,x)和实际回归任务之间的联系难以确定，同时这个值也容易受到实验者选择的损失函数以及伪标签的影响。其次，这种方法不需要选择损失函数，而是采用最小化KL 散度的方式替代了最小化损失函数这个步骤，这种方法可以直观反应预测概率分布和真实概率分布之间的差别。在下一节，本文将会给出一般性的回归模型，并将其与基于孪生网络的跟踪算法相结合。

4.1.1 一般性方法

本小节提出了一种有效的办法来训练网络，从而预测概率分布。首先给出在得到输入x 情况下预测输出y 的概率分布p(y|x,θ)：

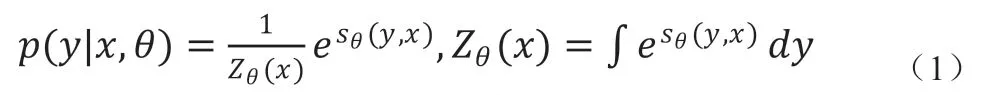
由于sθ(y,x)本质上来讲是置信度预测值，也是输入和输出关系被神经网络所转化为的一个标量值，这个式子表达的就是将这个值转化为概率密度，然后通过归一化常数进行调整和局部减少操作。

在参数训练方面，算法无需选取一般的Loss 函数，或者用负对数似然的方法来描述条件真值概率分布P(y|yi)与预测的条件概率值分布p(y|x,θ)之间的差异，而是选用KL 散度来将这两个概率分布的差异量化为标量值，KL 散度的一般性定义可以写为：

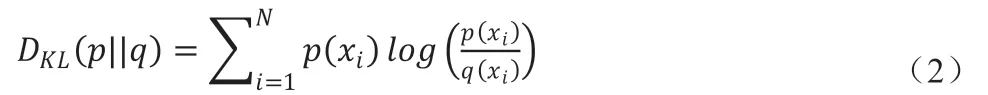
其中q(xi)是事件的近似分布，而p(xi)是事件的真实分布。根据式子，KL 散度的取值是从0 到无穷大的，近似分布与真实分布之间差异越小，KL 散度的值也就越小，反之亦然。在给出KL 散度的一般性定义之后，就可以给出用于训练网络来训练参数的KL散度：

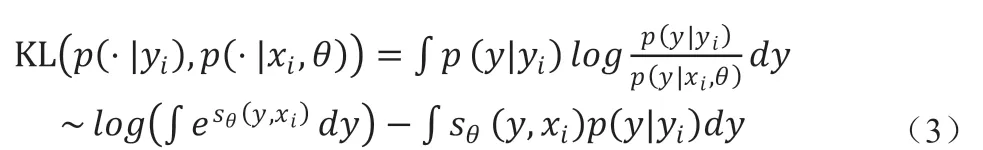
通过最小化KL 散度值，就可以获得与真实分布最匹配的预测概率分布参数。

5 模型训练

5.1 数据集处理

本算法使用ILSVRC2015 竞赛所用数据集进行训练。视频序列总量大概为4500 多组，分为前80%和后20%，分别进行训练和测试。选取该数据集是因为其中很多数据拥有人工标记，可以省去手动打标记的时间。对于每一个视频帧，本算法对边缘部分进行了裁剪并填充，从而保证输入图像为255*255*3 的RGB 图像。如图3所示。

5.2 算法框架流程

整个算法框架的执行流程如图4所示。

本算法可以分为两个环节。首先是进行离线模型训练，然后是进行在线目标跟踪。在模型训练环节中主要是数据的预处理和网络的训练。在目标跟踪环节中，首先给出待跟踪目标在视频首帧中的中心坐标和目标框尺寸，并为此建模。之后在视频的后续帧中持续执行跟踪任务，并输出目标框的位置坐标。

5.3 回归模型训练

在本算法执行目标跟踪的过程中，涉及两个回归任务，下面给出两种回归任务模型构建方法。

5.3.1 目标中心回归本算法采用网络采样的方法来训练目标的KL 散度值。其中条件真值密度可以设置为高斯分布。对于回归中心的分支预测权重模块，可以通过KL 散度损失函数和正则化来优化。之后本算法进行了快速下降结构的优化，并采用了二阶泰勒展开去近似优化目标。这是基于一个事实：线性预测中的目标函数是凸的，同时也因为梯度相关信息，所以可以这么做。

5.3.2 边界框回归

表1：模型测试指标分数

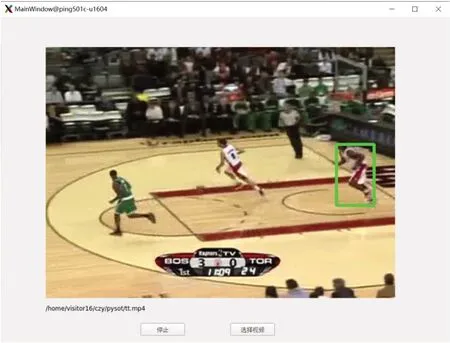
图6：篮球运动员跟踪效果演示

对边界框的回归模型采用和孪生网络中类似的结构，并应用本文使用的一般性概率公式进行优化。之后本算法采用了负似然估计的方法进行损失估计，并且使用近似方法扩展了概率设置。

6 实验结果分析

本文对改进后的基于概率回归的孪生网络目标跟踪方法在多个数据集上进行了训练和测试。所有实验均在AMD Ryzen51600x3.6GHz，16GB 内存和 NVIDIA GeForce RTX2080 显卡的PC 上运行。操作系统为Windows，采用Pytorch 1.7.1 作为机器学习库，编程语言为Python 3.6。

经测试，跟踪器能够达到40FPS 的跟踪速度。我们保存了模型训练每迭代2000 次取得的准确率（AUC）分数，绘制了模型迭代次数与准确率之间的关系。其中准确率是预测正确样本与总样本数量之间的比值。如图5所示。

将本模型与目前流行的孪生网络跟踪算法进行横向对比，涉及的算法模型有全卷积孪生网络目标跟踪算法（SiamFC），基于干扰物感知的孪生网络跟踪算法（DaSiamese），基于概率回归的孪生网络跟踪方法（PrSiamese）。评价指标有准确率（AUC），期望平均重叠率（EAO），健壮性（Robustness）。测试集基于VOT2018 数据集，其中对各个模型进行了测试并统计总体结果。其中各个评价指标评价表如表1所示。

从指标上来看，在孪生网络跟踪器中使用概率回归替代置信度回归是一种有效的优化手段。

6.1 系统演示

笔者搭建了简单的前端框架来实现跟踪过程的可视化，效果图如图6所示。

7 结语

本文首先分析并列出了目标跟踪领域的机遇和挑战，这些问题主要有背景快速变化和干扰、光照变化、物体的模糊和多尺度变化等。在分析目前主流跟踪算法的优劣点之后，提出一种基于区域推荐孪生网络的目标跟踪算法，并对其进行优化。本文采取概率回归的方法来替代传统目标跟踪中的置信度回归方法， 将Siamese 网络构架与基于概率回归的模型相融合，经测试算法模型在遇到干扰的情况下依然有较好的表现。

展望未来，本算法依然有可以改进之处。首先本文实验数据集有限，没有在足够的训练集上进行训练。可以预想，若对模型进行充分训练，则算法的泛化性能将会更好。同时本文中的概率模型仅运用在了基础的孪生网络上，未来可以和更多更复杂的孪生网络模型进行融合，这也是一个重要方向。