一种基于形状特征与SVM的列车故障连接件识别方法

孙美卫

（泉州经贸职业技术学院 信息技术系，福建 泉州 362000）

2018 年我国铁路货运量接近40 亿吨，列车货运是国家货物运输的重要组成部分，同时大批量、高频率的列车调配给其故障检测提出了更高的要求。目前，货运列车的故障检测及排查主要以人工现场勘察为主，该种检测方式劳动强度大、主观性强，难以保证检测质量。基于机器视觉的货车故障图像检测系统（Trouble of moving Freight car Detection System，TFDS）可有效克服人工检测的局限性，该系统采用智能算法与自动化装备以提高列车故障的检测效率。虽然该技术离工程应用还有一定距离，但其具有重要的研究价值[1-2]。

基于图像的TFDS 研究已经取得较大进展，张洪健提出了一种识别算法以解决货车螺栓丢失故障，该算法采用自适应中值滤波，LBP 特征以及模式选择来有效识别货车螺栓部位故障状态，取得一定效果，但是其受环境影响较大[3]。孙国栋等提出了一种基于几何特征的形状匹配算法以解决列车集尘器定位问题，该算法基于形状特征与改进的曼哈顿距离来计算识别算法的相似性，具有很强的抗刚性变化能力以及鲁棒性，但是该算法缺乏泛化能力[4]。Sun 等采用卷积神经网络完成货运列车的部分故障检测，取得了一定的效果。该方法在质量较差的环境中也有较高的精度与鲁棒性，但是深度学习网络需要海量的样本是制约其推广的最大局限[5]，其他相关的研究将不再列出。

本文研究对象是列车的连接件，如图1 红色矩形框所示，主要用于连接车体一些重要的结构件，如液压杆、插销、挡键等，防止其松动，脱落，因此连接件是货运列车安全的重要纽扣。由于连接件存在较大的安装误差，且受外界环境的光照干扰，故难以通过初级的特征识别算法定位所在区域。综合图像与机器学习的研究成果，提出了一种基于形状特征与支持向量机（Support Vector Machine，SVM）的连接件识别算法。该算法采用形状特征来提高识别与定位的鲁棒性，引入SVM 来加强识别判别模型的泛化能力，且识别算法几乎不受伸缩、旋转、平移等几何刚性变换的影响，具有较强的适应性。

图1 TFDS 采集的列车连接件图像

1 连接件识别算法总体方案

1.1 连接件图像识别的流程

提出的连接件识别算法是以目标形状为主体进行的研究，其总体识别算法流程如图2 所示，首先通过相机实时采集货运列车底部相应区域的图像，采用阈值处理以抑制光照对算法轮廓提取性能的影响，然后基于极半径的生成轮廓的形状特征，且用直方图对其形状进行量化处理，再引入SVM 判别学习模型对连接件进行识别。学习模型主要分为训练与预测两个阶段，训练阶段用于生成具体的判别模型，由于SVM 是监督学习，因此要提前对样本空间对正负样本进行标记，然后对各个轮廓进行类别预测，对预测结果为正样本类型的目标记录其中心位置，完成连接件的识别[6]。

图2 列车连接件识别算法总体流程图

1.2 目标图像预处理

大多数TFDS 论文注重形状识别算法的研究，并不专注于环境变化对目标轮廓的提取，而轮廓获取是整个研究的基础。针对这一问题，本节采用门限阈值处理来获取目标的轮廓信息。

基于上述分析，选择多个阈值进行连接件目标的分割，进而提取其轮廓，具体的步骤如下：

（1）通过实验，选择所有成功分割目标的阈值中值作为最终的分割阈值T，本文选取T=80，预处理后的效果如图3(a)所示。

（2）为保证采集图像轮廓的细节，多阈值图像空间的第1 层采用低连接阈值的Canny 进行边缘检测，边缘检测如3(b)所示。

（3）为抑制光照对连接件识别算法效果的影响，后续会对图像进行均衡化处理。

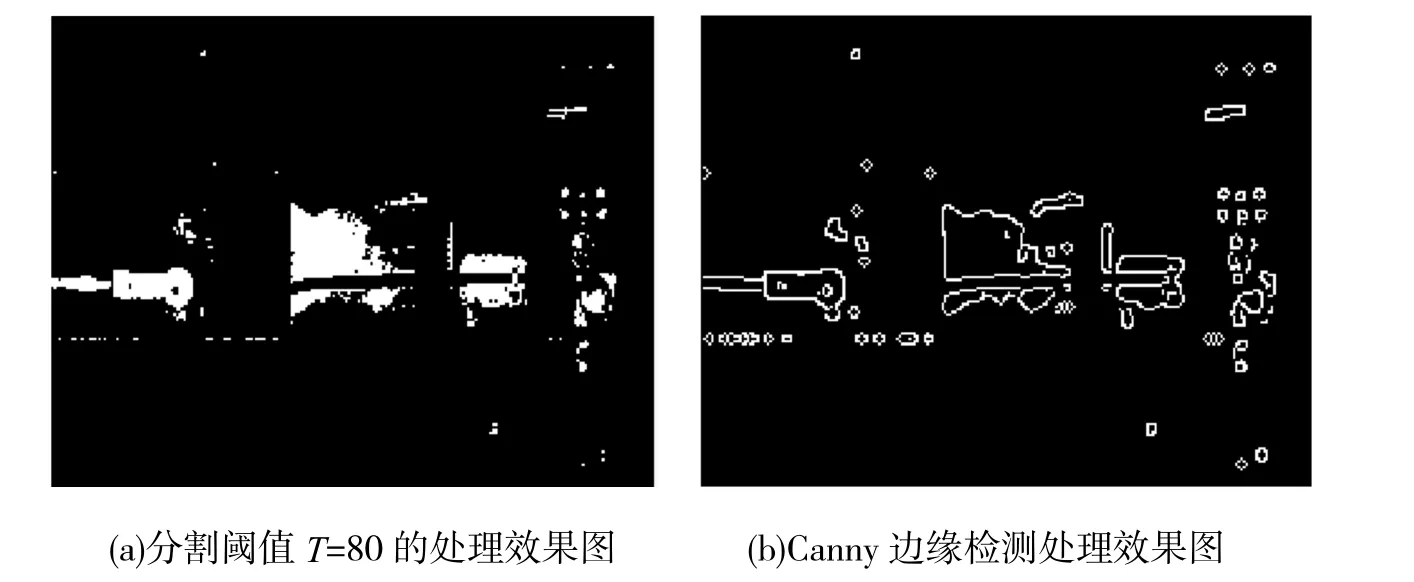
图3 列车连接件预处理效果图

2 识别算法描述子

2.1 特征描述

从式(1)可看出，fi描述的是轮廓采样点与形心的相对位置关系，且相对关系不会随着目标刚性变换的影响而发生波动。即使目标发生平移、缩放、旋转，单个采样点的向量值也不会受到影响。以连接件的形状为例（如图4(a)所示），现简要说明特征向量的描述过程，连接件是由左边矩形与右边圆形两个基元共同组成。约定变化波形以最远点为起点，逆时针方向为正方向，首先波形处于波峰位置，随着矩形上边离形心距离越近，波形向下延伸，然后进入弧形区域，波形逐渐向上爬升，遇到圆的下弧面，波形下降，再经过波形的临界点，波形开始上升，最后过渡到出发的起点。连接件的轮廓提取图与特征向量波形图如图4(d)标准图示例波形所示，基本符合理论分析。同时可以发现连接件由于图像质量的影响，最远点的位置并不是完全确定的，有可能会发生畸变，因此最远点来寻找分布波形的映射关系可能会发生匹配错位。

图4 列车连接件形状特征分布

但是在目标形状特征构造中存在以下问题：（1）由于拍摄工况的差异，目标的尺度与类型目标存在维度差异，造成轮廓采样点的数量不同，在形状特征向量中表现为维度差异，见图4(d)标准图示例波形与维度变化示例波形。（2）识别的目标由于列车的抖动，位置可能会发生旋转，造成特征起始点的错位，在特征向量上表现为波形的相位的偏差，如图4(d)标准图示例波形与旋转图示例波形。因此直接将特征输入给SVM 判别模型，会削弱分类器的识别精度，不利于学习模型的实际判别。针对以上问题，在2.2 节采用直方图量化的方法解决这个问题，规整后的特征波形如图4(e)所示。

2.2 特征量化

通过上述分析，目标的形状特征维度难以统一。若直接引用，不仅无法输入到特定的SVM 判别模型，而且由于特征权重不同造成学习判别模型下降，因此，该节引入直方图对特征进行量化及维度规整，详细的步骤如下。

（1）根据式(2)计算出目标的形状分布特征，记为 fn= { fn| fin, i = 1,2, …, N}，经过归一化后，值域fn∈ (0,1)，N 表示形状特征的取值数，对于每个形状目标都不一定常数。

（2）对特征量 fn包含L 个bin 的直方图，因此每个bin 的值域为：[( l -1)/ L, l / L]，l 为统计直方图bin 的数量索引，初始值为1，若存在一个特征量落入对应的bin 值区域，该bin 的计数器加1，其值初始化为0。

图4(e)是连接件在各种姿态下（见图4(a),(b),(c)）形状特征分布图，可以看出量化后的梯度特征基本不受几何变化的影响，分布基本重合。抗干扰能力很强，分布线重合。特别说明直方图bin 的数量与特征分布信息复杂结构有关，与目标的采样点以及统计范围没有关系，在SVM 的判别模型中发现，在bin 大于25后，基本可以得到理想的实验结果，增加bin 值会减少识别算法的实时性，因此本文取bin=30。

3 连接件判别模型

经过推导可知，引入拉格朗日乘子求导获取模型参数，模型中具体的参数定义可参考文献[11]。最终得到的模型为

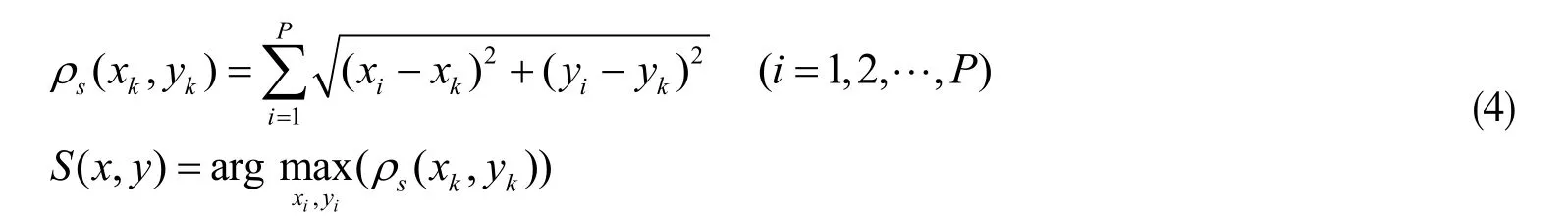
该节通过引入线性核函数使得低维线性不可分x 转化为高维线性可分，从而实现SVM 对高维特征的线性分类，为进一步提高SVM 的对伪样本的容错性，引入松弛变量来估计训练中错误样本对分类面的影响，其目标函数为

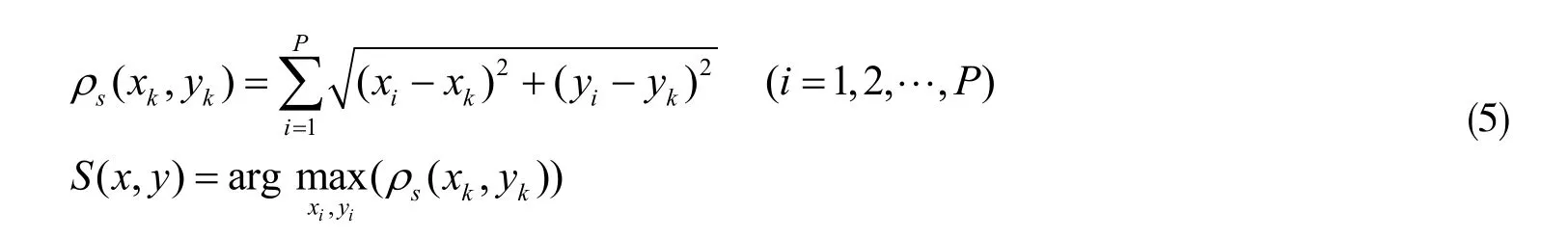
通过上述参数与样本训练完成SVM 的判别模型后，SVM 具有预测连接件类别的功能，，若判别为正样本类型，则其为连接件，否则不为连接件类型，完成连接件的识别。

4 实验结果和分析

为了验证识别算法描述子的描述特性，以连接件为例，选择在不同姿态下（缩放、旋转）的相似度值进行验证，其描述子相似度函数如式(6)所示，计算结果见表1。

CM,T表示模板M 和测试目标T 之间的匹配值，h 表示特征量化后的直方图的对应的分布值，K 表示bin的数目，并且取K=30。根据式(6)，计算的不同姿态下的连接件的匹配值如表1 所示。

表1 各种几何变换下的识别描述子值

从表1 可看出，提出的识别算法描述子基本上不受几何变换的影响，值的偏差也在很小的数量级内，因此，该识别算法描述子受几何变换的影响很小，具有一定的稳定性。采用SVM 学习模型密度估计定位连接件示意图如图1 矩形标记所示，证明了提出的识别算法能够适应外界的复杂环境。

5 结束语

为实现TFDS 的货运列车连接件的智能检测，提出了一种基于形状特征与SVM 的识别算法。该算法首先采用实验门限阈值以抑制光照对识别性能的影响，且取得了不错效果。然后，本文采用形状特征来提高连接件识别与定位的鲁棒性。最后，引入支持向量机来加强识别判别模型的泛化能力。该识别算法几乎不受伸缩、旋转、平移等几何刚性变换的影响，具有较强的适应性，但是该算法稳定性与实时性是今后的主要工作。