视均质潜山油藏不规则边界产能模型及影响因素

王瑞娟，徐铜浩，龚郁峰

（成都理工大学能源学院，四川成都 610059）

随着我国对能源需求的逐渐增加以及油气勘探开发的不断深入，加之常规油气藏的数量有限，非常规油气藏的勘探开发显得越来越重要[1]。视均质潜山油藏属于典型的非常规油气藏类型，储量规模较大，历史开采数据表明其具有较高的产能，对我国石油的未来开采方向具有重要的指导意义，但由于视均质潜山油藏储集空间形态复杂多样[5-8]，渗流场分布非均质性强且潜山油藏储层产能和组合关系差异大，因此，没办法合理且有效地对视均质潜山油藏进行开发。

视均质潜山油藏是一种特殊类型的基岩油藏，这类油藏具有岩性致密，储层非均质性强，直井开发动用程度低等特点，因此潜山油藏开发方式的研究也显得日益重要。本文通过开展视均质潜山油藏不规则边界产能模型测试，从渗流力学基本原理出发，建立视均质潜山油藏不规则边界产能预测模型并分析产能影响因素，研究表明，分析井筒储集系数、复杂边界形态、表皮系数对视均质潜山油藏不规则边界单井直井产能的影响，通过现场数据验证了本文建立的数学模型的可靠性。本篇文章的研究结果能够进一步为合理有效的潜山储量动用评价技术提供一定的支撑，为提高视均质潜山油藏不规则边界的采收率，实现稳产和高产具有十分重要的意义。

1 视均质潜山油藏储层不规则边界产能预测数学模型

由于建立边界积分方程时对基本解的利用方式不同，边界元法一般可分为直接法和间接法两类。直接法是指用具有明确物理意义的变量来建立边界积分方程，从这个方程解出来的就是未知的边界值。间接法则不用边界的待解边界值作为未知函数，而是在无限大区域内沿着该问题的计算边界配置某种点源分布函数作为间接的待解变量，它对计算区域的影响是一系列点源影响函数（基本解）的叠加。间接法的待解点源分布虽然往往是虚构的，但其计算效果与直接法完全相同，而公式比较简单[2]。本文选用直接法进行复杂油藏系统渗流问题。应用边界元理论求解渗流问题时，其边界元基本解应满足方程（1）。

对于P 点，其压力响应函数PD（P，u ）应满足油藏渗流微分方程（2）。

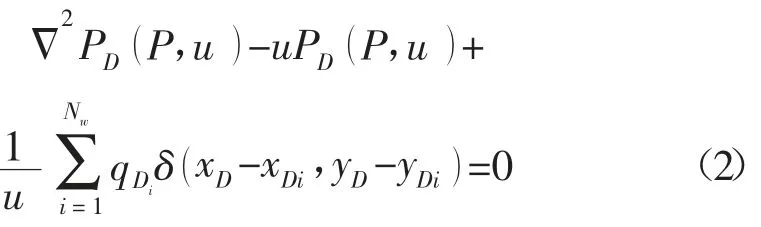
在研究区域内积分、用格林积分性质的第二公式及δ 函数的性质将式子化简，则区域积分公式可以简化为边界上的积分公式（3）。

将边界Γ 分割成Nb个单元段，以单元的端点作为边界元的节点（G 和P 代表的点），假设单元内的点按线性规律分布，为避免单元段节点成为奇异点，把节点附近的边界看成以节点为中心的一段圆弧，则边界Γ分割后其边界积分方程可以表示为[9]：

式中：θk-与边界节点处几何形状相关的常数，定义βk为边界Γk-1与Γk的内角。

1.1 视均质潜山油藏复杂边界形态边界元积分方程的求解

在积分单元Γi上建立无因次局部坐标系ξ，坐标原点位于中点），坐标轴的正向指向节点的反方向。

其中：l－距坐标原点的距离；li－线性元Γi的长度，－1＜ξ＜1。

函数PD在单元段内按照线性规律变化，根据线性插值公式可得到任意一点的PD值：

其中：PDi、PDi＋1－边界单元上Γi的两端点函数值。

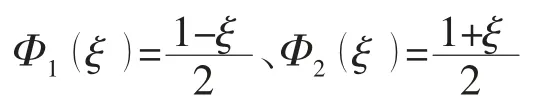
将上式代入边界积分公式（4）得公式（8）。

边界积分公式（8）可以变形为公式（9）。

边界积分方程（9）可以简化为：

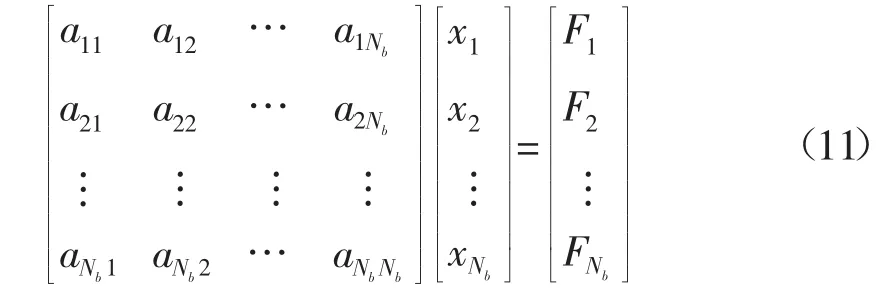
其中：xi为或PDi，Fi为 包 含及其他已知项的常数项。

未知的边界变量被计算出来后，便可利用边界积分方程（12）计算研究区域内任意一点的PD值。

2 视均质潜山油藏不规则边界储层产能影响因素

从图1 可以看出视均质潜山油藏顶底封闭压力导数曲线和双对数压力响应，从双对数曲线中可以看出，直井渗流有两个流动阶段：早期纯井筒储集阶段和过渡流动阶段。第一个阶段，在压力和压力导数双对数曲线上表现为斜率为1 的直线段,该阶段压力和压力导数曲线主要受油藏早期井筒储集效应的影响；第二个阶段，在压力导数曲线表现为一驼峰，该阶段压力和压力导数曲线主要受油藏表皮系数的影响；中期径向流动阶段，在压力和压力导数双对数曲线上压力导数曲线出现水平段且值为0.5，该阶段反映了水平方向上的系统总径向流动；实际过程中由于不同参数的相互影响，有些渗流阶段有可能被掩盖[10]。

图1 s 对井底压力响应曲线的影响

2.1 井筒储集系数对油藏产能的影响

井筒储集系数对视均质潜山油藏无因次产能的双曲线坐标影响关系图（见图2），井筒储集系数对视均质潜山油藏无因次产能的笛卡尔坐标影响关系图（见图3），井筒储集系数对产量的影响主要体现在排采阶段的初期，井筒储集系数越大，过渡流动段的驼峰越高，无因次产量曲线值就越大，中后期产量曲线基本重合。

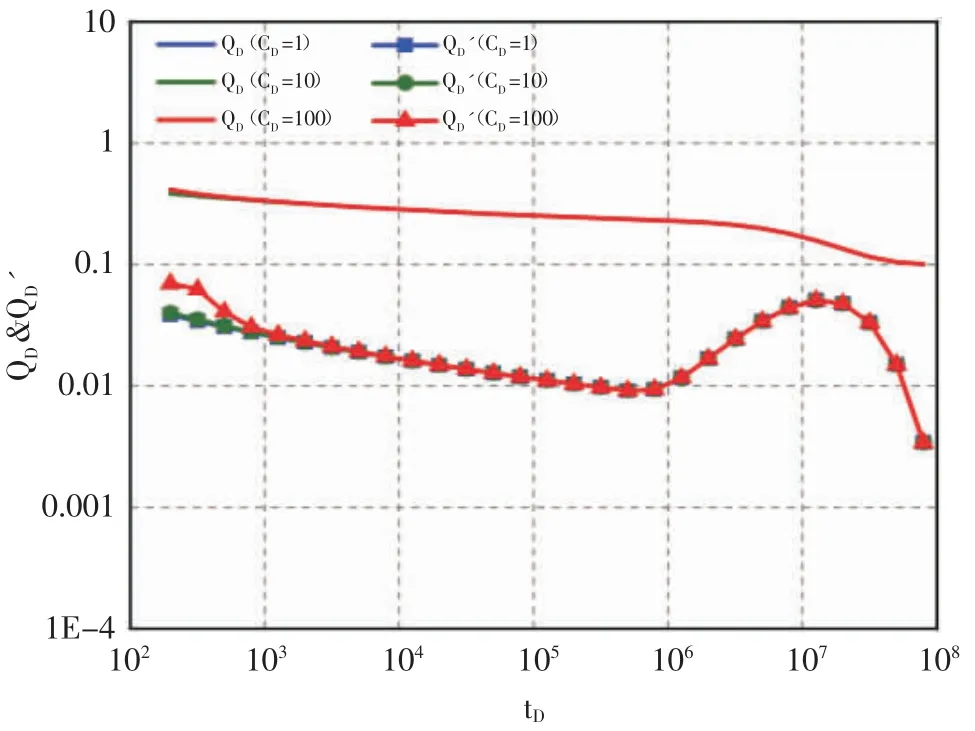
图2 井筒储集系数对视均质油藏无因次产能影响因素（双对数坐标）

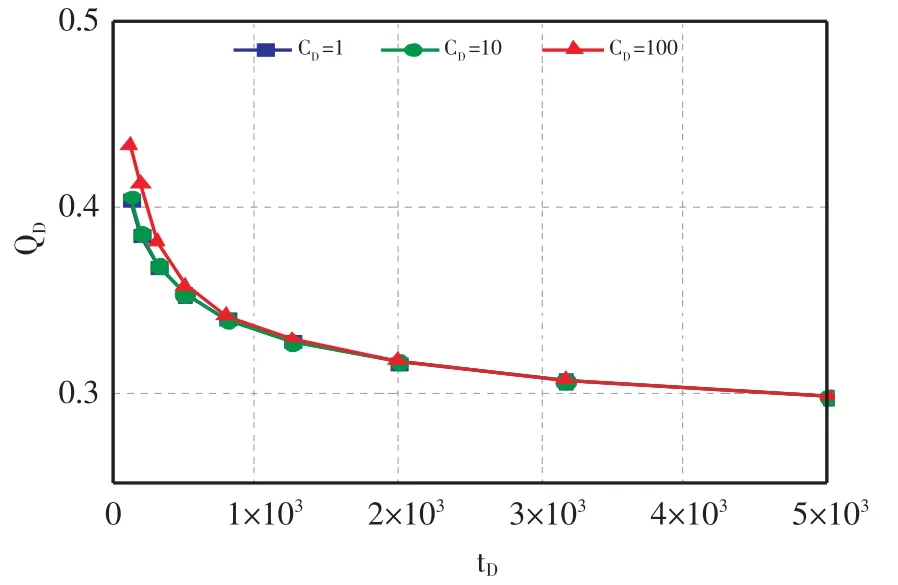
图3 井筒储集系数对视均质油藏无因次产能影响因素（笛卡尔坐标）

2.2 不规则边界形态对井底产能的影响

为了研究不规则边界形状对视均质潜山油藏产能的影响，特设计了正方形、矩形、六边形、五角星形等多种边界，具体边界形态（见图4～图7）。利用边界元程序绘制了视均质潜山油藏复杂边界形态无因次产能双对数曲线（见图8），由图8 可以看出，边界形态对产能和产能导数有一定影响，主要影响排采阶段后期产能递减规律，五角星形边界递减速率最快，矩形边界最慢[11-18]。

图4 正方形边界

图5 矩形边界

图6 六边形边界

图7 五角星形边界

图8 视均质潜山油藏复杂边界形态不同外边界双对数曲线图

边界大小对视均质潜山油藏无因次产能的双曲线坐标影响关系图（见图9），边界大小对视均质潜山油藏无因次产能的笛卡尔坐标影响关系图（见图10），边界距离对产量的影响主要体现在排采阶段的后期，影响后期产能递减规律，产量递减曲线上出现类似的水平台阶，边界距离越大，无因次产量曲线值越小，前中期产量曲线基本重合。

图9 边界大小对视均质油藏无因次产能影响因素（双对数坐标）

图10 边界大小对视均质油藏无因次产能影响因素（笛卡尔坐标）

2.3 表皮系数对油藏产能的影响

表皮系数对视均质潜山油藏复杂边界形态无因次产量双对数影响关系图（见图11），表皮系数对视均质潜山油藏复杂边界形态无因次产量笛卡尔坐标影响关系图（见图12），表皮系数对视均质潜山油藏复杂边界形态无因次产量影响较小，表皮系数越大，无因次产量越高。

图11 表皮系数对视均质潜山油藏复杂边界形态产能影响因素（双对数坐标）

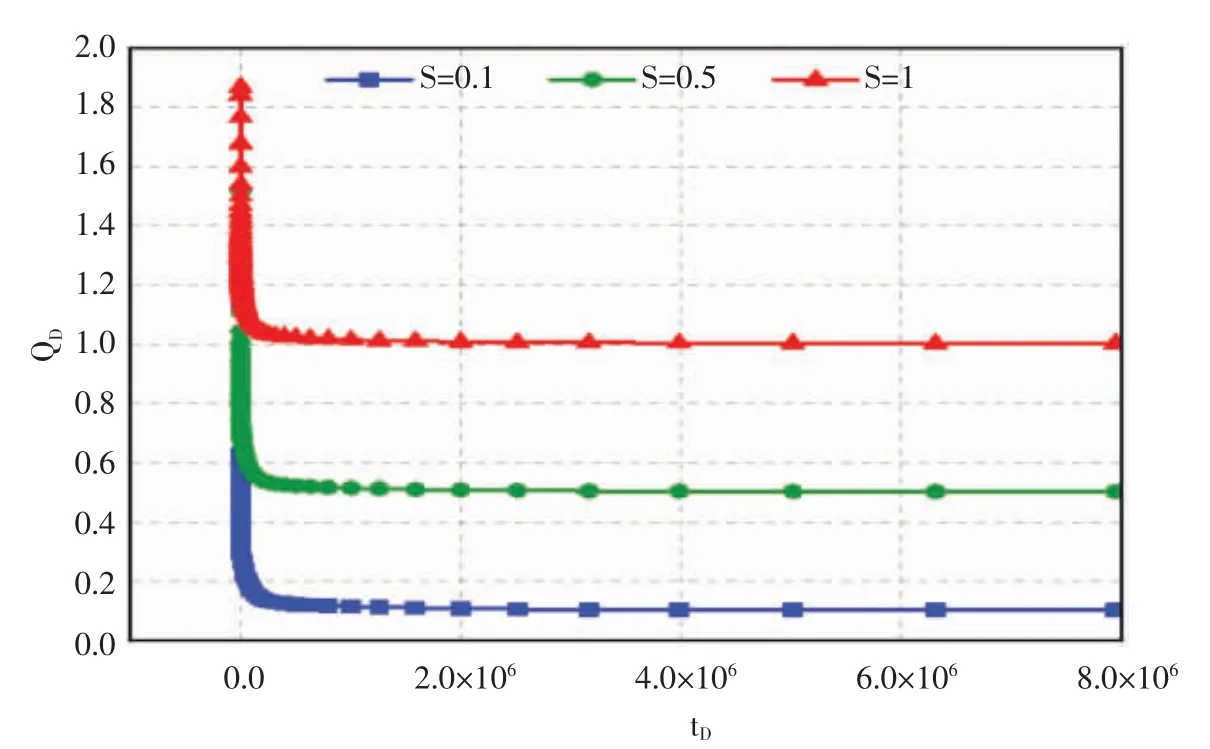
图12 表皮系数对视均质潜山油藏复杂边界形态产能影响因素（笛卡尔坐标）

3 现场应用

渤深6-1 井于2013 年1 月1 日投产，由河口采油厂采油三矿采油二队负责开采，地层原油密度为0.450 7 g/cm3，原油黏度为0.20 mPa·s，体积系数为3.053，饱和压力为39.83 MPa，压缩系数为5.12×103MPa-1。

利用本文建立的理论计算模型和分析软件，对该井进行了动态分析，渤深6-1 井选取2013 年1 月2日－2013 年2 月7 日的生产数据进行拟合[19，20]，从拟合效果来看（见图13），井口压力和产气量拟合程度较高，表明本套理论研究与实际开采过程较为吻合。拟合结果表明，该井地层压力7.78 MPa，表皮系数为1.34，井筒储集系数为0.006 4，边界为486.4 m，原始地层压力为8.64 MPa，初期实际产量为13.8 m3/d，计算产量为14.03 m3/d；后期实际产量为13.5 m3/d，计算产量为12.69 m3/d。

渤深6-2 井于2013 年1 月1 日投产，由河口采油厂采油三矿采油二队负责开采，初期产液量10.5 t/d，后期最高产液量5.7 t/d，累积产液量28 104.3 t。

图13 渤深6-1 井单井产量和压力拟合效果图

通过本文所建立的理论计算模型及分析软件，对该井进行了动态分析，渤深6-2 井选取2013 年1 月2日-2013 年2 月7 日的生产数据进行拟合，从拟合效果来看（见图14），井口压力和产量拟合程度较高，表明本套理论研究与实际开采过程较为吻合。拟合结果表明，该井地层压力为11.56 MPa，表皮系数为1.18，井筒储集系数为0.006 4，边界为1 008 m，原始地层压力为11.56 MPa，初期实际产量为10.5 m3/d，计算产量为9.99 m3/d；后期实际产量为9.6 m3/d，计算产量为11.44 m3/d。

渤深6-12 井为本工区的一口水平井，该井2013年1 月6 日投产，初期排水127 m3/d，初期产液量45 t/d，后期最高产液量9.0 t/d，累积产液量33 896.5 t。

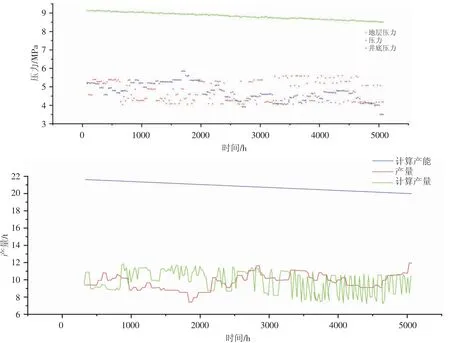
图14 渤深6-2 单井产量和压力拟合效果图

图15 渤深6-12 单井产量和压力拟合效果图

通过本文建立的理论计算模型和分析软件，对该井进行了动态分析，渤深6-12 井选取2017 年6 月16日-2018 年1 月23 日的生产数据进行拟合，从拟合效果来看（见图15），井口压力和产量拟合程度较高，表明本套理论研究与实际开采过程较为吻合。拟合结果表明，该井地层压力为11.56 MPa，表皮系数为1.2，井筒储集系数为0.008，边界为792 m，原始地层压力为17.6 MPa，初期实际产量为14.1 m3/d，计算产量为12.91 m3/d；后期实际产量为13.5 m3/d，计算产量为11.12 m3/d。

4 结论

（1）在视均质潜山油藏地质模型的简化基础上，从渗流力学基本原理出发，建立视均质潜山油藏不规则边界产能预测模型并分析产能影响因素，通过对渤深6-2 的单井产能评价，验证了本文所建立的数学模型的可靠性较高。

（2）视均质潜山油藏不规则边界产能影响因素分析结果表明：井筒储集系数越大，产量递减速率越快；边界距离影响后期产能递减规律，边界距离越大，无因次产量曲线值越小；表皮系数越大，无因次产量越高。