瞬变电磁法救援井方位角误差分析与仿真

杜芙蓉，党瑞荣，王 港

（西安石油大学电子工程学院，陕西西安 710065）

在实际钻井工作中，油井发生井喷是钻井作业中最为严重的灾难事件[1，2]。而救援井是控制井喷事故最有效的方法，在实施中，救援井和事故井套管的距离探测、方位测定是救援的关键工作[3，4]。文献[5]采用瞬变电磁探测系统对事故井和救援井的相对位置进行分析，设计出了定位与测距作业过程，给出了确定连通点和初始探测点的选择办法。文献[6]采用注入电流法，通过分析事故井套管上汇聚电流产生的环形交变磁场分布规律，从而得到事故井与救援井的相对位置关系。但是，这种方法需要大功率的电流源，如果探测端的地层电阻率较高，那么在事故井套管上的汇聚电流就很小，这将严重影响事故井套管的探测精度。

针对上述问题，本文在瞬变法理论的基础上，通过建立瞬变电磁法救援井探测模型，分析仪器探头接收线圈的二次涡流场信号与两井相对距离的对应关系。并提出了事故井空间几何定位法，利用救援井与事故井在不同深度的距离计算相对方位，实现事故井的空间定位，为提高救援井与事故井连通率提供支持，从而提高定距。

1 救援井瞬变电磁探测原理

以法拉第电磁感应定律为物理基础，建立救援井井下分层模型（见图1）。将磁芯作为最内层介质，采用双发一收的探头结构，发射线圈和接收线圈位于第二层的空气媒质中，仪器外护管位于第三层，从第四层到第六层分别是钻井液、冲洗侵入带与原状地层。其中磁芯、空气、仪器保护套是有源区，救援井周围的介质井液、冲洗带、地层是无源区。

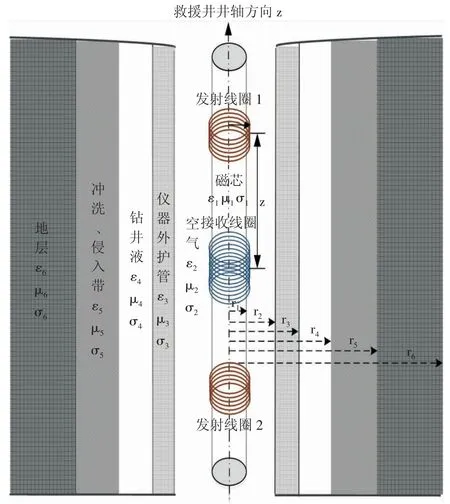
图1 救援井井下分层模型

假设第j层介质的电参数和几何参数分别为（μj，εj，σj）和rj。引入磁矢A，考虑到柱坐标的对称性，Ar＝Az＝0，令，将二次场满足的齐次亥姆霍兹方程表示为[7]：

其中：kj为波数。求解式（1），可得第j 层介质中的二次场矢量势大小为：

其中：NT－发射线圈匝数；IT－发射电流；Aj、Bj-待定系数）－第一类和第二类1 阶复宗量贝塞尔函数；z－发射线圈与接收线圈之间的距离。

结合矢量磁势与场量关系式，可得z 方向磁场分量的值为：

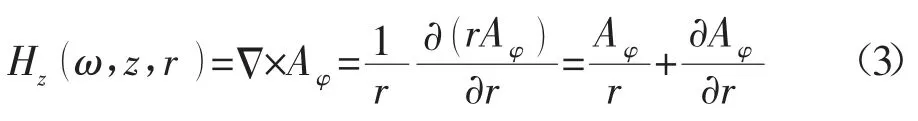
将（2）式代入（3）式，可得接收线圈z 方向的磁场强度。再根据各层介质的边界条件，可推导出位于介质1 中接收线圈频域的感应电动势为：

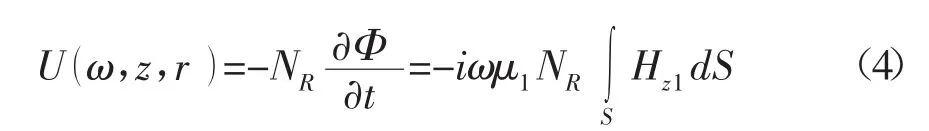
其中：ω－角频率；NR－接收线圈匝数；S－感应场接收线圈有效面积。采用G－S 逆变换法将（4）式从频域到时域进行转换，可得接收线圈时域的感应电动势：

其中：z-已知收发距；Kp-G-S 方法的滤波系数，越多的G-S 逆变换点数对应的结果越精确，与解析解之间的误差越小。分析可知式（5）中的未知量仅为t 和r，其中t 为采样时间，r 为磁芯中心轴与异常地质体之间的距离，当固定采样时刻t 时，两井相对距离与感应电动势便呈现对应关系，通过对接收线圈感应电动势的信号进行采集、分析和处理之后可获取与事故井套管相关的信息[8]，以反演出事故井套管与救援井的相对距离。

2 事故井套管空间几何定位方法

根据救援井中接收线圈的响应对两井的相对距离进行反演，利用相对距离，采用两点空间几何定位方法对两井的实时方位信息进行计算。救援井与事故井套管的方位计算流程（见图2）。

图2 救援井与事故井套管的方位计算流程

救援井两点空间几何定位模型（见图3），假设事故井套管垂直，以A'为原点，A'D'为x 轴，A'B'为y轴，A'A 为z 轴，建立空间三维坐标系。救援井沿A-KC'方向钻进，与事故井套管异面。救援井倾角指救援井与事故井套管的夹角，在图中即为AA'与AC'的夹角α。当探测仪器位于A 点时，根据探头探测到的感应电动势反演的救援井与事故井的相对距离为AB，记为r1，当仪器下放距离L 至K 点时，由感应电动势反演的两井相对距离为r2，r2与r1异面。r1在平面A'B'C'D'上的投影是A'B'，r2在平面A'B'C'D'上的投影是OB'，仪器从A 到K 的下放距离L 在平面A'B'C'D'的投影是A'O，则事故井套管与救援井的方位角即为A'B' 与B'O 的夹角β。以此类推再以K 点为原点，救援井的轨迹为对角线建立三维直角坐标系，直到实现救援井与事故井的交汇连通。

由几何关系可知，当仪器位于救援井中A、K 两个位置处时，事故井套管与救援井的位置关系在三角形A'B'O 中满足勾股定理，利用算法定位公式得到的方位角为：

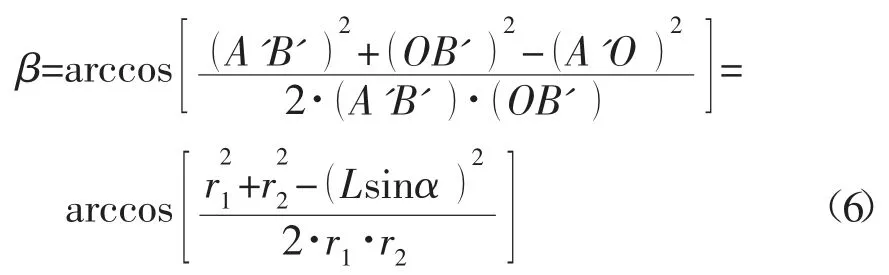
当探头处感应电动势反演的两井距离多次不变时，则说明两井的姿态处于平行状态，此时，只需利用方位角来判断救援井与事故井的相对位置[9]。

图3 救援井空间几何定位模型

分析式（6）的方位角计算公式，探测距离、救援井倾角以及深度步长均会对方位角的测量产生影响，对方位角与这三种因素之间的关系进行分析，从而得出对方位角的影响规律，以便降低方位误差。

3 方位角影响因素仿真分析

在救援井方位探测方法中，根据空间几何定位模型推导出方位角的理论计算公式，但并未结合实际测试情况对方位计算精度的影响因素进行分析。下面以某口正钻救援井720 m 处的真实钻井信息为例，利用MATLAB 软件对影响方位角的各个因素进行仿真分析。当测井仪器处于深度为720 m 的位置，根据接收线圈上的感应电动势反演的两井距离r1=4.955 0 m，r2=4.882 9 m，取步长L=1 m，根据先验信息得到的救援井倾角α=4.991 3°，由此得到的方位角β=0.567 2°。

3.1 救援井倾角对方位角的影响

井斜角是指井眼轨迹的斜度，范围一般为0°～180°。常规定向井的井斜角一般小于60°，这是因为在救援井中井斜角过大会导致测井作业工具无法下放至探测位置，影响测井作业的速度。为了研究救援井井斜角对方位角的影响，根据实际测井数据进行如下仿真。

当α 变化时，变化范围为0°～180°，变化间隔是1，保持r1、r2的值不变，即r1=4.955 0 m，r2=4.882 9 m。在不同深度步长的情况下，观察救援井倾角随方位角误差的变化情况（见图4）。图中的纵坐标方位角误差为公式计算的方位角与720 m 处真实方位角之差。

由图4 可知，当救援井倾角在0°～180°变化时，随着救援井倾角的增大，方位角误差呈现增大-减小的趋势。救援井倾角在α=90°时方位角误差达到最大，约为34.93°。当救援井倾角接近于0°和180°时，即救援井与事故井的相对姿态接近于平行状态时，方位角误差最小。当事故井不垂直时，如果下井前没有足够详细的信息而假设事故井是垂直的，就会导致倾角误差，进而会产生方位角误差，所以在下井前应尽可能多的获取与事故井套管方位有关的信息来降低方位误差。

图4 救援井倾角对方位角的影响

3.2 深度步长对方位角的影响

当L 变化时，变化范围为0.9～3 m，变化间隔是0.1，保持r1、r2的值不变，即r1=4.955 0 m，r2=4.882 9 m。在不同救援井倾角的情况下，观察深度步长随方位角误差的变化情况（见图5）。

图5 深度步长对方位角的影响

分析图5 可知，当深度步长在1～3 m 变化时，随着深度步长的增大，方位角误差逐渐增大。步长为1 时，方位角误差最小，步长为3 m 时，方位角误差最大，方位角最大误差约为2.4°。在深度步长的变化范围内，救援井倾角为85°时，方位角误差曲线斜率最大，最大方位误差约为34.69°，救援井倾角为5°时，方位角误差曲线斜率最小，最小方位误差约为0.04°。说明计算方位的深度步长会对方位精度产生影响。所以在假设事故井垂直的基础上，通过自动调节两点之间的深度步长可以提高救援井与事故井方位信息的计算精度，实现更为精确的接近并探测事故井套管。

3.3 两井相对距离对方位角的影响

当r1变化时，变化范围为4.8～4.965 m，变化间隔是0.005，保持L、α 的值不变，即L=1 m，α=4.991 3°。方位角误差随救援井与事故井套管相对距离的变化情况（见图6）。

图6 两井相对距离对方位角的影响

由图6 可知，当两井相对距离r1在4.75～5.05 m变化时，方位角误差随着相对距离的增大呈现先增大后减小的变化趋势，方位角最大误差约为0.56°，方位角误差较小，说明了前期距离反演的准确性。但需要说明的是，距离信息是根据感应电动势反演得到的，当探测距离过近或过远时，由于磁信号发射能量的分散性或仪器探测范围的局限性就会导致距离探测的误差较大，从而引起方位角的偏差。

4 结论

基于瞬变电磁法救援井探测理论，通过建立救援井与事故井套管的两点探测定位模型，根据空间几何关系确定救援井的方位角。对于方位角的影响因素通过MATLAB 仿真分析，结果表明：

（1）在步长和两井相对距离一定的情况下，随着救援井倾角的增大，救援井与事故井的方位角误差在一个周期内呈现先递增后递减的趋势。

（2）在救援井倾角和两井相对距离一定的情况下，救援井与事故井的方位角误差随着步长的增大而增大。

（3）保持救援井倾角和步长不变，随着救援井与事故井的相对距离增大，其方位角误差先增大后减小。