黄麻纤维毡吸声模型构建与试验验证

林 萍，徐晓美，吴晓莉,Lee Heow Pueh

（1.南京林业大学 汽车与交通工程学院，南京210037；2.新加坡国立大学 机械工程系，新加坡117576）

与传统的合成纤维相比，天然纤维具有来源广泛、绿色环保等优点，其天然形成的相互贯通的多孔结构使得声波更容易发生能量耗散，从而使其具有较好的吸声性能。黄麻纤维是天然纤维中性能较优异的一种，常用作汽车顶棚、内门板骨架、座椅背板等内饰件基材和声学包装材料[1]。但黄麻纤维毡材的吸声性能多数通过试验获取，其吸声预测模型尚需进一步研究，以更好地指导黄麻纤维产品的声学设计与应用。

吸声性能通常以吸声系数为评价指标，材料的吸声系数可以通过描述特征阻抗和复数传播常数的材料基本特征参数推演得到，即通过构建材料的吸声模型预测得到[2-4]。目前，应用较多的多孔材料吸声预测模型有两种，即以Delany-Bazley（简称DB）模型[3]为代表的经验模型和以Johnson-Champoux-Allard（简称JCA）模型[4]为代表的唯象模型。经验模型仅需测量流阻率一个非声学参数，用归纳统计的方法，通过拟合大量阻抗管试验数据，分别建立特征阻抗、传播常数与流阻率和声波频率之间的幂指函数关系，因此模型简单，能快速预测结果；但是经验模型没有考虑孔隙的微观结构，且每种经验模型仅适用于预测一种类型的材料和某些频率范围的吸声系数，因此不具有普遍适用性。唯象模型不同于经验模型，它考虑了黏滞和热传导效应等微观因素对声能的影响，引入多个特征参数描述材料性质，构建了多孔材料微观结构和吸声系数之间的关系，因此计算精度较高且参数物理意义清晰，目前得到了更多的应用[5]。Soltani 等和Taban 等[6-7]研究了凤兰尾植物纤维和天然椰壳纤维，对比分析了JCA吸声模型以及其他模型对纤维材料特征阻抗和吸声系数的预测能力，结果表明JCA吸声模型对于天然纤维的预测效果最好。Bansod等[8]基于试验数据预估了毡状黄麻材料的非声学参数，并利用JCA吸声模型计算了其吸声系数，研究表明，基于JCA吸声模型计算的吸声系数与试验结果吻合较好。

鉴于此，本文对基于JCA吸声模型的黄麻纤维毡的声学有限元模型构建与验证开展研究，以进一步考察JCA模型用于预测黄麻纤维毡吸声性能的效果，以及所建立的黄麻纤维毡声学有限元模型的可靠性，从而更好地为黄麻纤维毡的产品设计与应用提供理论指导。

1 JCA吸声模型

JCA吸声模型引入5个物理特征参数：流阻率σ、孔隙率φ、曲折因子α∞、黏性特征长度Λ和热特征长度Λ′，又称为五参数半经验模型。流阻率是最为重要的影响材料吸声性能物理参数之一，定义为空气流经单位厚度多孔材料时所受到的阻力，单位为N·s/m4。孔隙率计算的是多孔材料中饱和流体（一般为空气）的体积与材料的总体积之比，数值在(0，1)之间，一般孔隙率高的材料，即取值接近于1，吸声性能较好。曲折因子是体现孔隙结构复杂度的因子，反映声波在材料厚度方向上传播时实际通过路径与直线路径之间的偏差。黏性特征长度和热特征长度分别描述了高频下孔隙中的流体与固体框架间的黏滞力大小和热交换程度，单位为μm。该模型对材料的动态密度ρe(ω)和有效体积模量Ke(ω)的描述见式(1)和式(2)。式

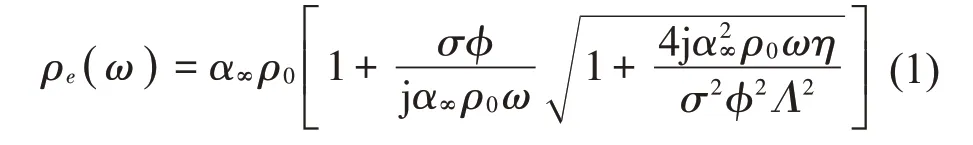
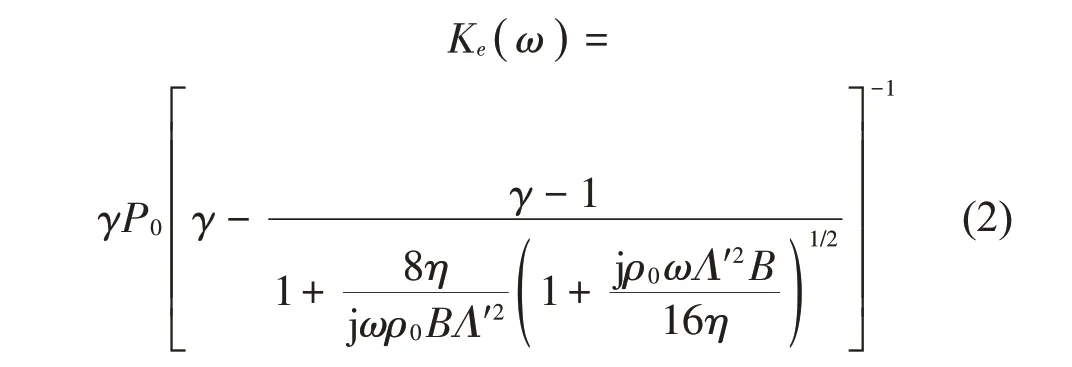
中：j为虚数单位，ρ0是空气的密度，B是普朗特数，P0是环境大气压，η是空气的动力黏度，γ是空气的比热容比，ω为入射波角频率，黏性特征长度Λ和热特征长度Λ′可写为

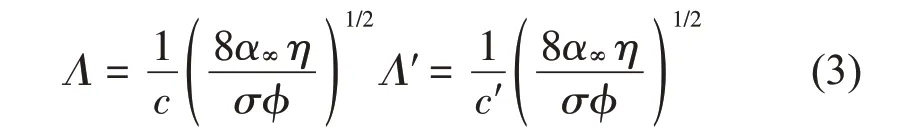
式中：c和c′是孔的横截面形状因子和尺度因子。

由式(1)和式(2)可表征材料的特征阻抗Zc(ω)和复数传播常数ke(ω)。

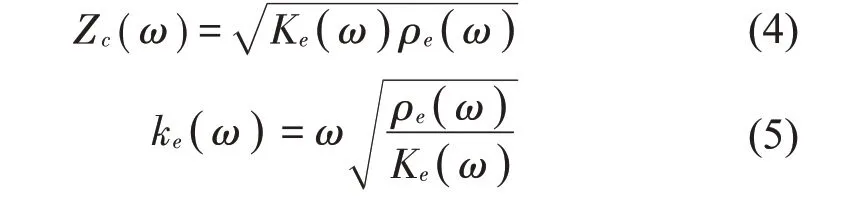
考虑厚度为d的多孔材料背衬刚性壁面的情况，吸声系数α可由式(6)至式(8)表达。

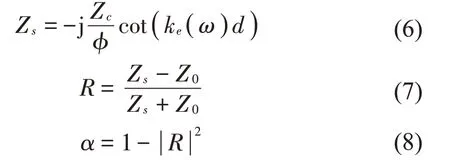
式中：Z0是空气特征阻抗，Zs是材料表面阻抗，R是声压反射系数。

2 吸声系数测试与参数辨识

为获得JCA吸声模型中的物理特征参数，本节利用阻抗管法对黄麻纤维毡进行吸声系数测试，并基于试验数据通过粒子群算法辨识得到相关参数。

2.1 试验样品

选取的黄麻纤维毡样品如图1所示。其经过开松混合和梳理成网工艺后堆叠加热粘合而成，在环境扫描电镜下的微观形状如图2所示。统计得到的纤维平均直径为23.67 μm。

图1 黄麻纤维毡样品

图2 黄麻纤维毡环境扫描电镜图

为方便后续阻抗管试验，将黄麻纤维毡制作成两个直径不同的圆形样品，样品直径分别与大、小阻抗管内径（100 mm 和30 mm）相匹配。需要注意的是，因为毡材质柔软，为避免样品和阻抗管间产生间隙泄露，使样品的直径略大于阻抗管内径，大样品直径为100.92 mm，小样品直径为31.5 mm，平均厚度为18.79 mm，平均密度为41.93 kg/m3。样品的孔隙率可以根据式(9)计算[9]。

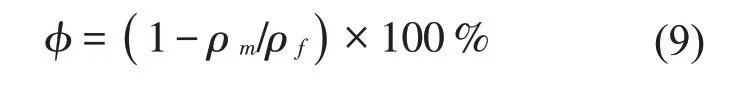
式中：ρm为样品的密度，ρf为黄麻纤维原材料的密度，为1 084.4 kg/m3，由此可得样品的孔隙率为0.96。

2.2 吸声系数测试

利用B＆K4206型声学阻抗管测试系统，基于传递函数法（ISO 10534－2:1998 基准）测量黄麻纤维毡的吸声系数。测量系统如图3所示，由两套阻抗管套件（内径分别为100 mm和30 mm）、功率放大器、声校准仪、PULSE分析软件等组成，扬声器安装在右侧半段管的顶端，被测样品放置在另一侧半段管中，调整尾部的螺杆使样品背衬刚性壁面。黄麻纤维毡在阻抗管中的安装如图4所示。

图3 声学阻抗管测试系统

图4 样品安装图

在阻抗管试验中，B＆K阻抗管的大直径管和小直径管分别负责测量250 Hz 至1 600 Hz 和500 Hz至6 400 Hz的偶数频率点的吸声系数。显然，在500 Hz 至1 600 Hz的频率范围内数据有重叠，考虑此间各个频率的权重，重叠频率段吸声系数的计算式如式(10)所示[10]：

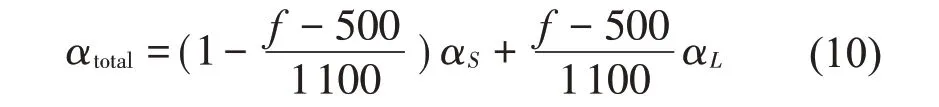
式中：αS和αL分别代表样品在小直径管和大直径管中测得的吸声系数。

黄麻纤维毡的吸声系数曲线如图5所示。由图5可以看出，黄麻纤维毡的吸声系数随频率的增加而增加，在高频范围内具有较好的吸声性能，其最大吸声系数可达0.82。

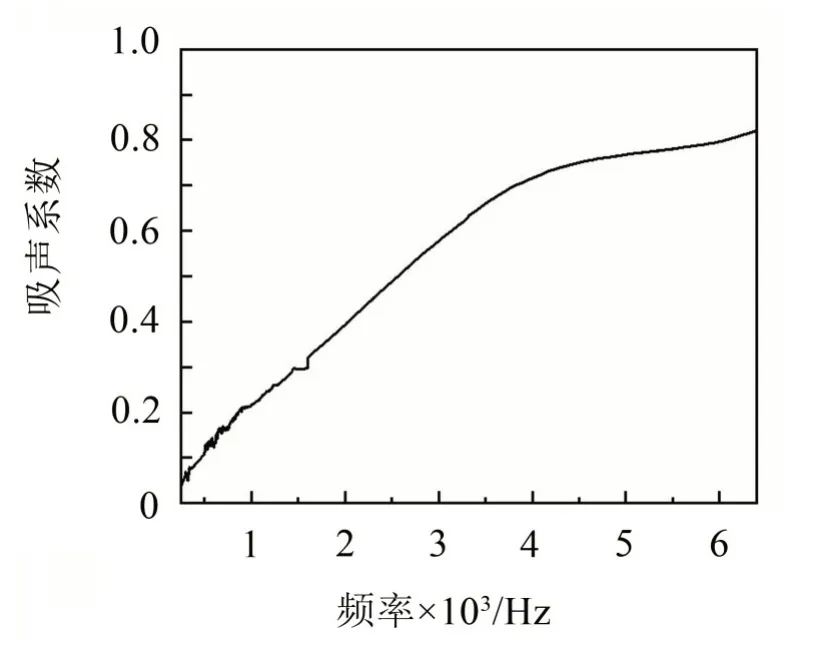
图5 黄麻纤维毡的吸声系数测试值

2.3 参数辨识

JCA吸声模型中有4个参数需要辨识，即流阻率、曲折度、黏性特征长度和热特征长度。其辨识思想是根据阻抗管测得的吸声系数与孔隙率，通过拟合模型逆推JCA模型中的未知参数。粒子群算法是求解声学参数逆问题的一种高效可行的算法[8]，因此本文采用粒子群算法进行参数辨识。算法的目标是寻求全局最优变量使JCA模型理论预测的吸声系数值与试验获取的试验值吻合程度最佳。基于最小二乘法，将各个频率下吸声系数实测值与预测值的差值平方和设计为目标函数，也称为适应度函数，适应度值越小表明预测值与实测值越接近，辨识的精度更高。JCA模型参数的辨识问题可以描述为：

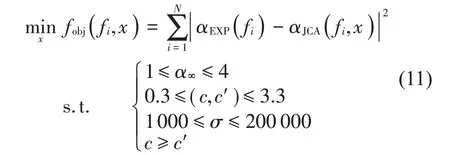
式中：fi表示250 Hz～6 400 Hz 之间的偶数频率，N是测试频率段的采样频率点个数。αEXP表示在各频率点测得的吸声系数，αJCA表示在各频率点用JCA模型计算时的取值。

在MATLAB 软件中编写相应的粒子群算法程序，设置算法参数：粒子个数为N=100，粒子维度为D=4，学习因子c1=c2=2，惯性权重为ω=1，迭代次数M=500。对算法独立运行30次，求出使理论计算值与实测值最接近的参数值作为最终的辨识参数，其辨识结果为：流阻率为12 742 N·s/m4，曲折因子为1，黏性特征长度为267 μm，热特征长度为267 μm。这些参数将作为下节黄麻纤维毡声学有限元模型中JCA吸声模型的参数输入。

3 黄麻纤维毡声学有限元模型构建

为考察采用JCA吸声模型预测黄麻纤维毡吸声性能的准确性，同时呈现黄麻纤维毡在声波垂直入射情况下的声压与声强分布情况，本节构建了黄麻纤维毡的声学有限元模型。

在COMSOL中黄麻纤维毡的建模过程如下：

（1）选择模块。为了减少计算量和节约时间，在模型向导中选择二维轴对称模型，调用声学-压力声学模块，选择频域研究。

（2）构建几何模型。在r-z平面内建立一个二维轴对称模型，如图6所示。从上往下分为3个域，依次是完美匹配层PML 域、声入射域和纤维材料域，高度分别为Hpml、Ha和H，半径都为R。声入射域和纤维材料域分别代表空气和黄麻纤维毡，建立PML域的目的是模拟材料处于无反射的空气域内。设置纤维材料域的尺寸与黄麻纤维毡的实测尺寸相同，具体数值为：H=18.79 mm，R=50.46 mm，Ha=100 mm，Hpml=20 mm。

（3）定义相关计算变量。式(7)中的声压反射系数在声场中可由散射声压Pscat与入射声压Pinc的比值表示，如式(12)所示[11]：

式中：Pscat等于总声压减去入射声压；aveop表示在入射端边界上定义的一个平均值算符，用于计算空气与材料交界处入射声压和散射声压的线平均值；因为事先不知道纤维材料中的入射场，所以散射声压表达式只在声入射域中有效，故需输入down作为边界的下部算符。确定声压反射系数后，即可根据式(8)计算材料的吸声系数。

（4）添加域材料。声入射域为空气，其属性参数直接用软件内置空气材料的默认数值。然后创建黄麻材料，用JCA吸声模型的5个物理特征参数表征。

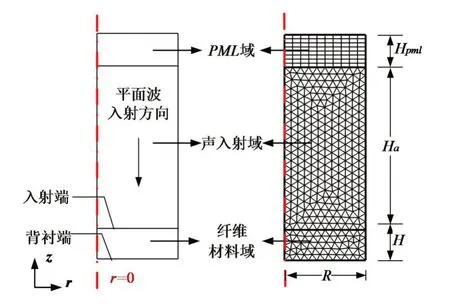
图6 二维轴对称模型图

（5）设置声场和边界。将“背景压力场”应用于声入射域形成声激励，设置入射声波类型为幅值为1 Pa的平面波，声波行进方向为-ez，用来模拟入射波从入射端垂直向下进入材料的情况。用“多孔介质声学”JCA吸声模型表征黄麻纤维材料，注意要将空气属性赋给流体，黄麻材料属性赋给多孔基体。考虑样品背衬刚性壁面的条件，在其背衬端施加硬声场边界，同时，因为模型预测的是声波垂直入射时的吸声系数，所以声入射域和材料域的右端边界也设为硬声场边界。

（6）划分网格。划分声入射域和纤维材料域网格时，要保证这两个域的网格尺寸不超过最小波长的六分之一，该模型仿真频率的最大值为6 400 Hz，即网格尺寸要小于8.93 mm。在模型中设定三角形网格划分，大小选择“较细化”，其最大单元格尺寸为5.14 mm，满足要求。采用映射的方式进行PML 域单元格划分，沿侧边划分8个单元。对黄麻纤维毡二维轴对称模型共划分了682个网格。

（7）频域研究设置。为方便比较理论仿真值与试验值，设置与阻抗管试验相同的频率范围和步长，即仿真频率范围为250 Hz 至6 400 Hz，仿真步长为2 Hz。

4 仿真模型验证与分析

构建完成黄麻纤维毡的声学有限元模型后，进行仿真运算，可得到如图7所示的吸声系数与频率的关系曲线。图7还通过对比呈现了由阻抗管试验得到的黄麻纤维毡的吸声系数曲线。

由图7可以看出，在整个分析频率范围内，根据有限元仿真得到的黄麻纤维毡的吸声系数曲线与根据试验得到的曲线具有较好的一致性，两根曲线几乎重叠在一起。这表明，JCA吸声模型能较好地描述黄麻纤维毡的吸声性能，基于COMSOL软件所建立的黄麻纤维毡的声学有限元模型是可靠的。

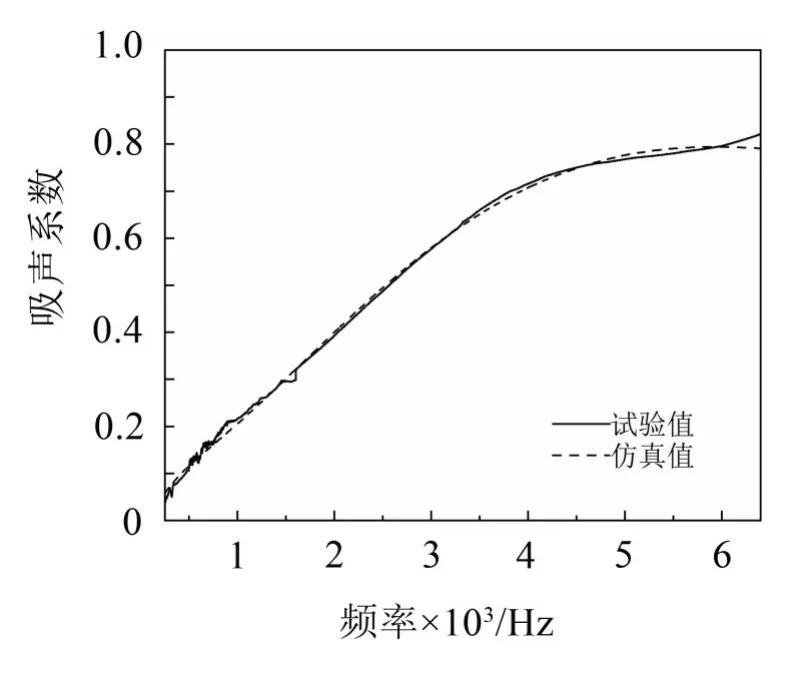
图7 黄麻纤维毡吸声系数试验值与仿真值比较

黄麻纤维毡在仿真环境下的最大吸声系数为0.794，对应的频率为5 930 Hz。为展现在此频率下有限元模型中各区域的声压与声能量分布，图8给出了频率f=5 930 Hz时空气域和纤维材料域内声场的声压级分布状况，图9给出了频率f=5 930 Hz时的声强矢量和声能分布情况。

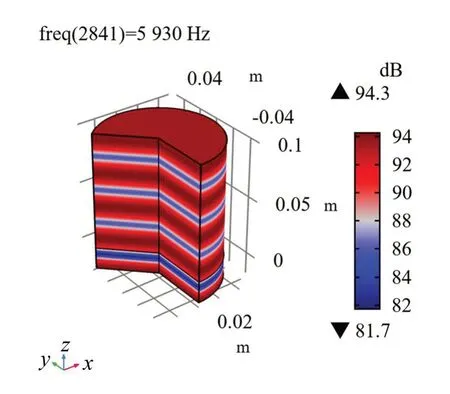
图8 频率f=5 930 Hz时各区域的声压级分布

由图8可以看出，纤维材料域的声压级明显低于空气域，最低声压级出现在纤维材料域内部，说明黄麻纤维毡具有良好的吸声性能。

由图9可以看出，在声入射域声强矢量的方向均垂直向下且长度都一样，对应的声能密度云图颜色未发生改变，可知声波在此区域没有发生能量损失，这与背景压力场设置的幅值为1 Pa的平面波的特性一致；而在纤维材料域内，声强矢量的长度沿着声波入射方向逐渐减小，与之对应的声能密度云图颜色由红色过渡变化为蓝色，表示声能逐渐衰减，这是因为声波通过纤维内大量孔隙时产生的黏滞耗散以及热耗散吸收了声能。

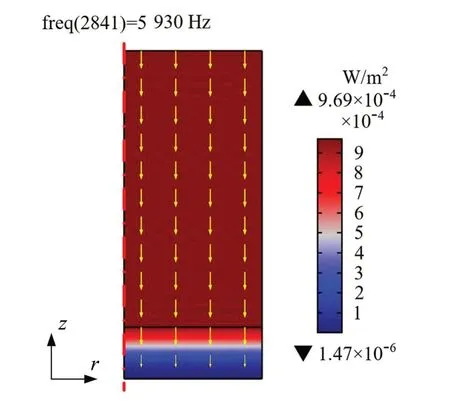
图9 频率f=5 930 Hz时各区域的声强矢量与声能分布

5 结 语

本文采用JCA吸声模型预测黄麻纤维毡的吸声性能，为获取黄麻纤维毡的物理特性参数，利用阻抗管对黄麻纤维毡进行了吸声系数测试，采用粒子群算法对JCA吸声模型相关参数进行了辨识，基于所建立的黄麻纤维毡声学有限元模型，仿真出黄麻纤维毡的吸声系数和声压与声能分布。研究表明，在高频范围内，黄麻纤维毡具有较好的吸声性能；JCA吸声模型能较好地描述黄麻纤维毡的吸声性能；基于COMSOL 软件所建立的黄麻纤维毡的声学有限元模型经过试验验证证明是可靠的，可用于植物纤维材料吸声性能的仿真分析，从而可指导该类产品的声学设计与应用。