高速列车车体抖振现象研究

韩兴晋，周劲松，厉鑫波，陈江雪

（同济大学 铁道与城市轨道交通研究院，201804 上海）

我国高速列车取得了高速发展，车辆舒适性研究不断进步，其中由于轮轨接触不匹配、悬挂参数不匹配、部件疲劳损伤等因素引起的车体异常抖振现象逐渐引起重视。曾京等建立了铁道客车振动模型，分析了弹性车体对客车振动的影响，提出车辆的1阶弯曲自振频率应远离构架的浮沉自振频率以减弱共振[1]，张晓阳等通过轨道状态测试、台架试验和悬挂参数对比等方法研究得出，轮轨匹配关系不良导致了高速列车的异常振动[2]，厉鑫波等基于ODS（Operational deflection shape）工作变形分析和轮轨匹配等效锥度理论提出转向架接近蛇行失稳是晃车的主要原因[3]，夏张辉等基于样条插值原理提出车辆模态频率的追踪方法，指出轮对模态与车体模态间的振型切换导致了车辆低频横向晃动[4]，宫岛等分析了车体弹性模态与转向架的耦合振动，提出车体弹性共振是由于垂向1阶弯曲频率接近车体点头频率引起的，在车体纵梁上安装阻尼器可以抑制车体的垂向振动[5-6]。周劲松等分析了车辆刚度对运行平稳性的影响，提出当车身刚度降低时，会出现明显振动[7]。

根据实际调研，某高速列车在运营线上运行时会出现车体抖振现象，表现为车体出现异常抖动、人感到脚部发麻、行李架出现挤压异响，严重降低列车的运行平稳性和乘客的乘坐舒适度。本文实测了该高速列车在运营线上的车体异常抖振加速度信号，将其与非异常抖振加速度信号的时频特征、Sperling平稳性指标进行对比，对抖振加速度信号进行工作模态分析(Operational modal analysis，OMA)并结合工作变形分析(ODS)结果识别车辆各阶模态对抖振变形的贡献量，分析了抖振时车辆的轴箱加速度信号和传递函数，归纳车体抖振现象的发生原因。

1 车辆测试试验设计

1.1 车体振动测试

以该高速列车实际运营线的一节MP车作为研究对象，依据《铁道车辆动力学性能评定和试验鉴定规范》（GB5599－1985）[8]，加速度计布置在车体地板二位端距车体中心线1 m 位置，测点布置如图1所示。采集运行全线的振动加速度信号，测试方向选择为横向和垂向，列车以AWO 模式运行，时速为140 km/h，采样频率为2 048 Hz。

图1 车体振动测点布置

1.2 车辆模态测试

对车辆进行模态分析可以求得各阶模态参数，包括频率、阻尼和振型，模态测点布置在转向架构架上方车体截面、车体中心截面以及转向架构架上，测点以能表征结构的大致形状为原则布置，测点布置如图2至图3所示。

图2 车体模态测点布置图

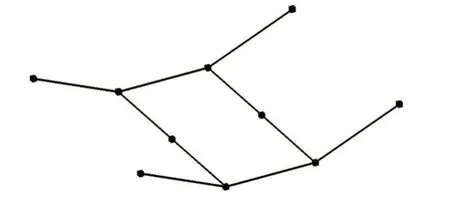
图3 构架模态测点布置图

1.3 传递函数测试

高速列车运行时，钢轨波磨和车轮磨耗引起轮轨接触不匹配，产生的激励通过悬挂系统传递到车体，为分析车辆抖振信号的传递特性，在轴箱、转向架构架、空气弹簧、车体地板位置布置加速度传感器，测点布置如图4所示。

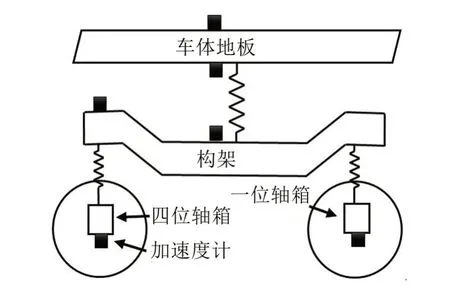
图4 传递函数测点布置图

以上测试中选取的加速度传感器参数如表1所示。

表1 加速度传感器参数

2 车辆测试结果分析

2.1 车体振动测试结果

基于该高速列车实际运营线获取车体抖振时的加速度信号特征，发现车体横向时域频域信号均异常，以图1所示车体地板测点为例，图5为在平稳运行和发生抖振现象时的横向加速度时域信号，从图中可以看出，车辆平稳运行时信号比较密集，而发生抖振时信号特征明显区别于平稳信号，呈现低频谐波信号特征，幅值相比平稳信号波动更大。

通常，时域信号比较复杂，频域能更清晰反映信号的频率成分，对抖振信号进行频域变换，与平稳信号进行对比，结果如图6所示。可以发现，车体发生抖振时，主频为10 Hz 附近的加速度幅值远高于平稳信号。

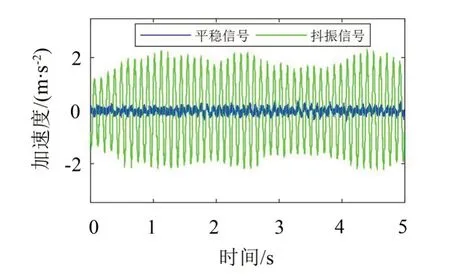
图5 横向振动时域信号

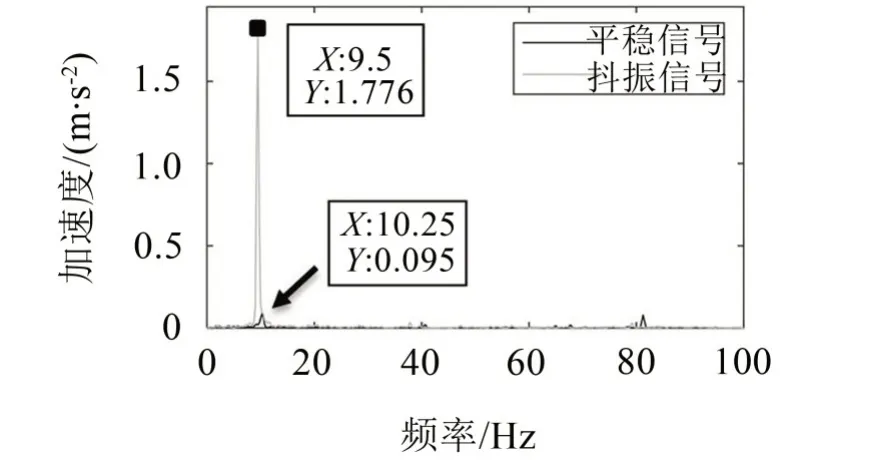
图6 横向振动频域信号

我国通常采用Sperling 提出的平稳性指标来评价车辆的运行品质，理论公式为式（1），Sperling指标值低于2.5为优，低于3为合格。表2为车体地板测点在平稳运行和发生抖振现象时的横向加速度Sperling指标计算值，可以看出，车辆在平稳运行时，横向Sperling值为1.57，而当车辆出现抖振现象时，Sperling值超过“合格”限值，说明抖振现象对车辆的运行平稳性有很大影响。

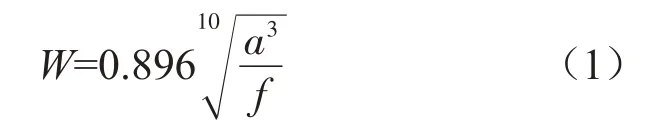
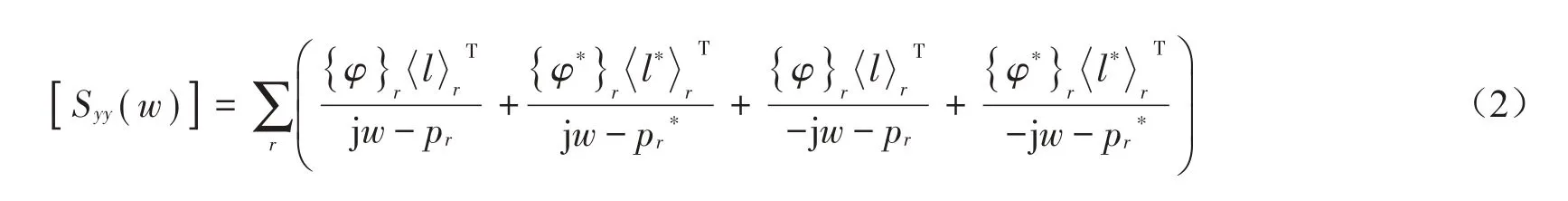
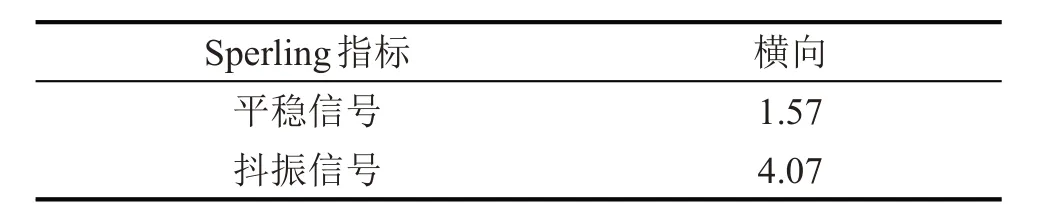
表2 Sperling指标计算值

2.2 车辆模态分析

工作变形分析（Operational Deflection Shape，ODS）也称为运行响应模态分析，其代表结构模态振型按某种线性方式叠加的结果，对抖振时车体和构架整体的加速度信号进行时域ODS分析，结果如图7所示，可以发现，在抖振区段，车体随构架蛇行运动而来回晃动，振动幅度较大。

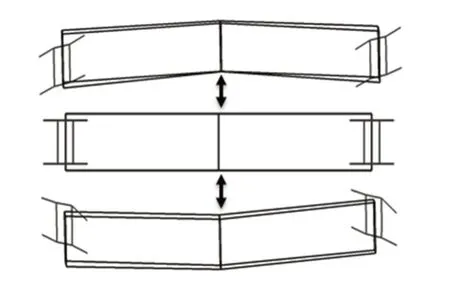
图7 抖振时域ODS分析

工作模态分析（Operational Modal Analysis，OMA）又称为环境激励模态分析，模态识别方法采用PolyMAX算法，也称多参考最小二乘复频域法，利用LSFD 法求模态振型，理论公式为式（2），对车体和构架整体的加速度信号进行OMA分析，共识别11阶模态，模态参数如表3所示。

表3 OMA分析模态表

其中：pr为系统的极点为工作参与因子向量，为模态振型向量。

为评价基于OMA 分析所得振型几何上的相关性，使用模态置信准则（MAC）来进行模态验证，理论公式为式（3），当MAC值接近1时，代表振型向量非常相关，校核结果如图8所示，可以看出，非对角线MAC值很低，任意两个振型相关性小，模态识别质量高。

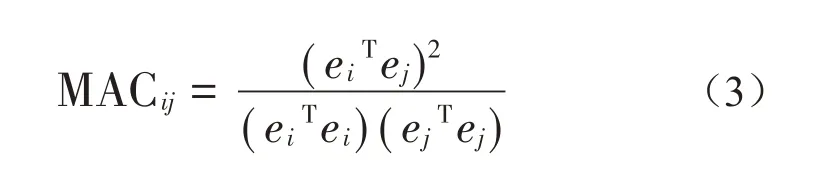
其中：ei、ej为振型向量。

为识别车辆各阶模态对抖振变形的贡献量，随机选取10个时刻，将基于OMA 识别得到的模态与工作变形ODS 进行比较分解，结果如图9所示。可以看出，车辆第1阶模态振型（9.461 Hz）对抖振变形贡献量最大，这与图6抖振加速度信号主频相吻合，第一阶模态频率为9.461 Hz，车辆振型与时域ODS特征相同，构架蛇行运动振型明显，车体随构架蛇行而同向蛇行运动。根据以上分析，推测构架由于受到轮轨不匹配引入的横向激励作用发生蛇行运动，车体受到构架向上传递的横向激励作用，出现抖振现象。

图8 MAC准则判定结果

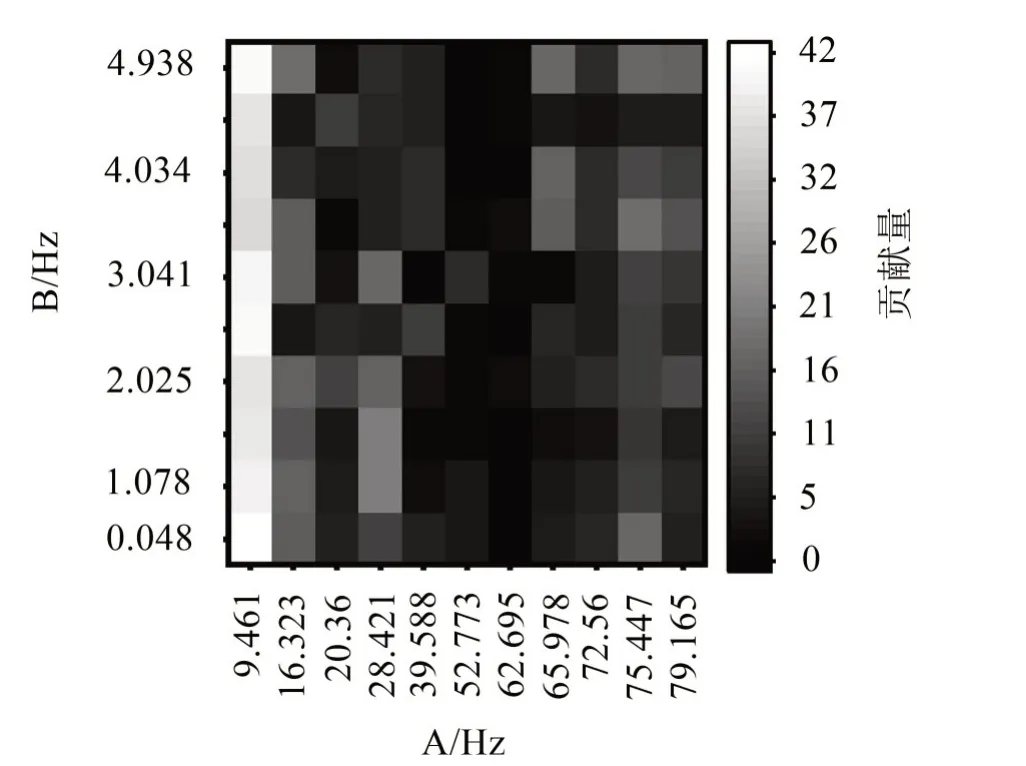
图9 模态贡献量分析

2.3 传递函数分析

为确定抖振发生时的轮轨匹配关系是否存在问题，取一位轴箱和四位轴箱横向加速度时域信号存在异常波动时的信号进行分析，如图10所示。可以发现一位轴箱和四位轴箱所受到的冲击存在明显时延，根据轴箱所受冲击的时延推算车辆运行速度为140 m/h，由此可见，轮轨匹配关系存在异常，使轴箱受到延时性冲击。

相干函数可以用来检测传递函数测量的有效性，取值为0～1，相干函数取值为1时，说明输出完全由输入引起，理论公式为式（4），依据图4所示传递函数测点布置，对轴箱-构架、空气弹簧下-空气弹簧上、空气弹簧上-车体地板横向加速度信号进行相干性分析，结果如图11 至图13所示。可以看出，抖振现象发生时，各传递环节之间的信号在10 Hz附近的相干性较好，而平稳运行时，各传递环节之间信号的相干性较差，故认为抖振区间内轮轨横向激励是引起抖振现象的重要原因。

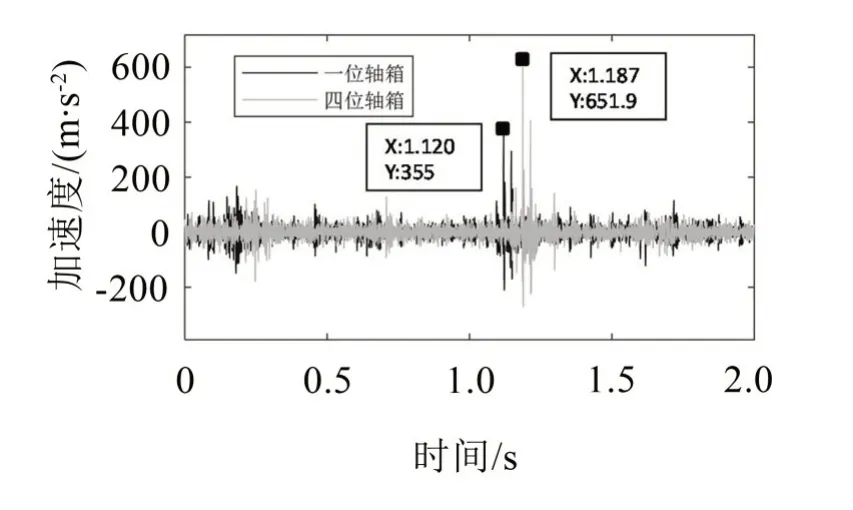
图10 轴箱信号时延分析

其中：Gxx为输入自功率谱，Gyy为输出自功率谱，Gyx、Gxy为互功率谱。

图11 轴箱-构架相干函数

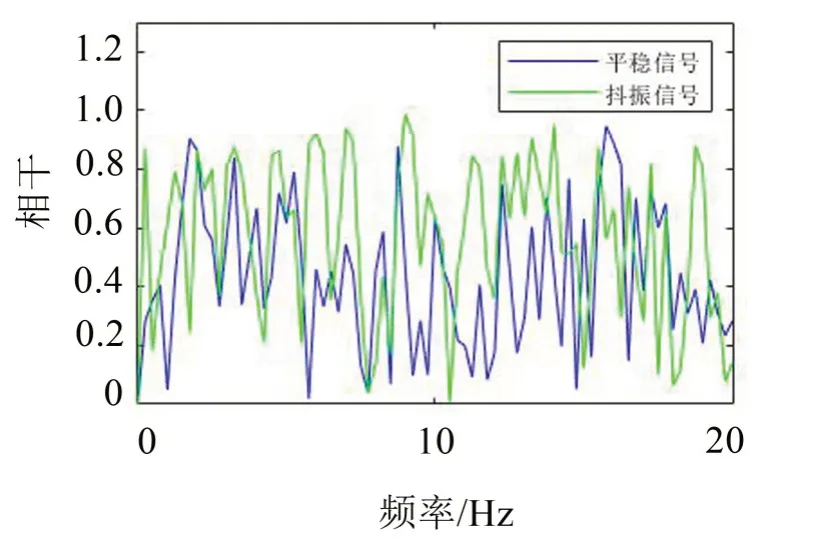
图12 空气弹簧下-空气弹簧上相干函数

3 结语

实测某高速列车在运营线上的车体异常抖振加速度信号，将其与非异常抖振加速度信号的时频特征、Sperling 平稳性指标进行对比，对抖振加速度信号进行OMA分析并结合ODS分析结果识别车辆各阶模态对抖振变形的贡献量，分析了抖振时车辆的轴箱加速度信号、传递函数，提出以下结论和建议。

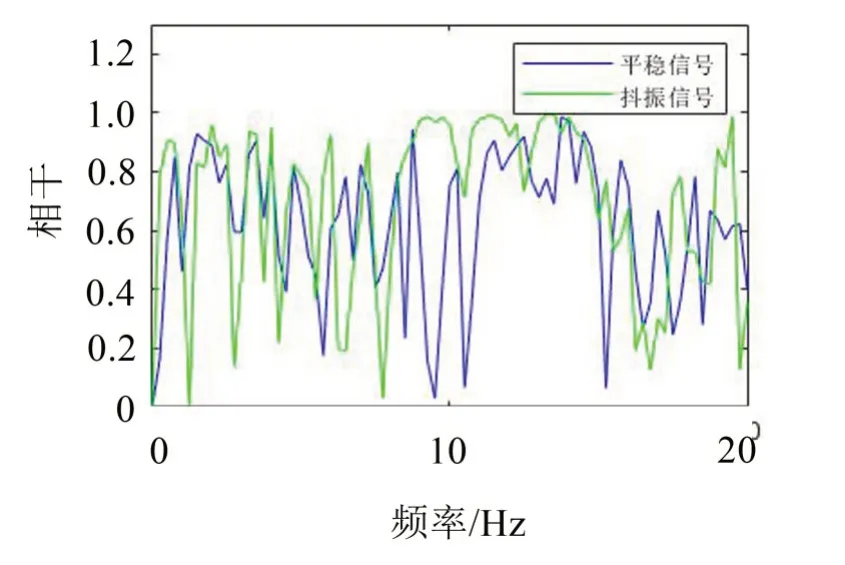
图13 空气弹簧上-车体地板相干函数

（1）此高速列车出现抖振现象的主要原因是轮轨接触不匹配引入冲击，产生的激励通过车辆悬挂系统向上传递，激起了频率在9.461 Hz处的车辆模态振动，使车体随构架蛇行运动而来回晃动，振动幅度较大，发生抖振。

（2）建议在综合考虑运营安全和工程实际的基础上，对抖振常发区间进行降速，缩短车轮和钢轨的检修周期，对踏面磨耗严重的车轮进行镟修，对波磨严重的钢轨进行打磨，保证轮轨匹配良好，抑制车体抖振现象，提高车辆运行舒适性。