Lamb波在铝板缝类缺陷检测中的应用

苗育茁，黄 浪，柯 耀，王 琪，陈汉新

(武汉工程大学 机电工程学院，武汉430205)

板状金属结构在各类机械装备中被广泛使用，尤其是铝合金薄板，在航空航天、高压容器等装备制造业得到广泛应用[1]。金属板材在加工的过程中会出现裂纹、气孔、折皱和分层等缺陷，长时间工作会导致金属结构内部的微小缺陷发展成宏观裂纹，最终造成结构断裂，严重时可能会导致装备的损坏，引发严重的灾难性事故[2-3]，近年来非线性Lamb 波检测技术越来越受到关注[4]。

李喜朋通过理论分析和测试实验，分析了采用Lamb波检测板中缺陷损伤的可行性[5]。艾春安等发现利用超声斜入射进行Lamb 波的激励是切实可行的，通过实验发现入射角对Lamb 波模态的影响很大，在工程应用中具有一定指导意义[6]。刘镇清对薄板的超声Lamb波传播特性进行了研究，并重点研究了超声Lamb 波的激发方法和板厚范围内的振动位移变化等，这些都为超声Lamb波在无损检测中的应用奠定了基础。

基于超声Lamb波的复杂性，在对缺陷信号进行检测时，对回波的信号处理成为本文的研究重点。本文建立了一个非线性超声检测系统。通过研究非线性波动方程，分析了二次谐波幅值与非线性系数之间的关系、超声非线性系数随缺陷深度和疲劳裂纹大小变化的关系，检测了铝合金板材中Lamb波随缺陷变化的规律，验证了采用该方法检测金属板材微缺陷的可行性。

1 非线性超声检测表征参数的选择

某一列的超声波信号在待测试件内部传播过程中，会与试件内部的缺陷相互作用，导致最终接收到的回波信号产生畸变，由于基波能量传输到谐波，因此会导致高次谐波的产生。假设在大振幅声波和小形变状态的情形下，当纵波在均匀固体中沿X方向上传播时，其一维纵波方程为

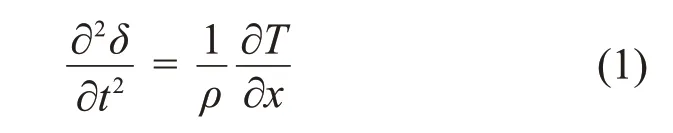
其中：δ为x轴方向上的位移，T(x,t)为x轴方向上的应力，ρ为材料密度，x为传播距离。结合应力-应变非线性关系T=∫E()1+βε+γε2+… dε、应变-位移关系以及声速-密度-弹性模量关系c2=，得到固体中的非线性波动方程为

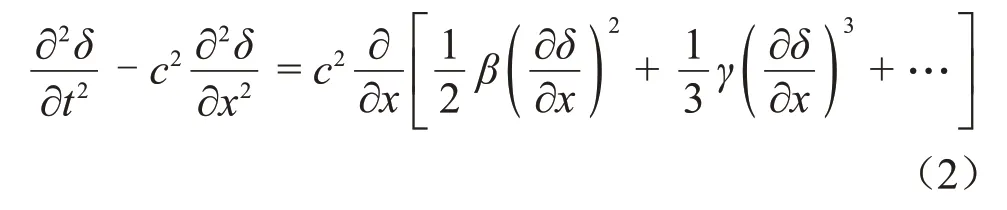
采用渐进分析法求解得到固体中的非线性声波方程的解为

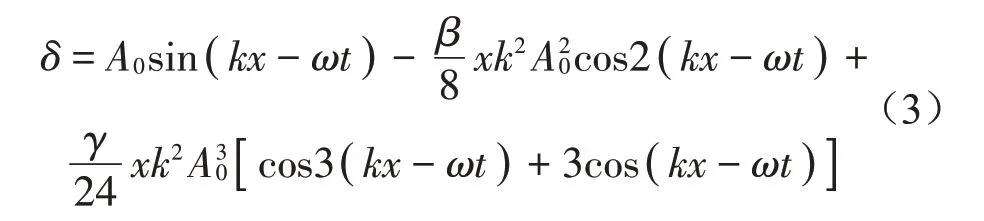
式（3）中基波幅值A1、二次谐波幅值A2和三次谐波幅值A3分别为

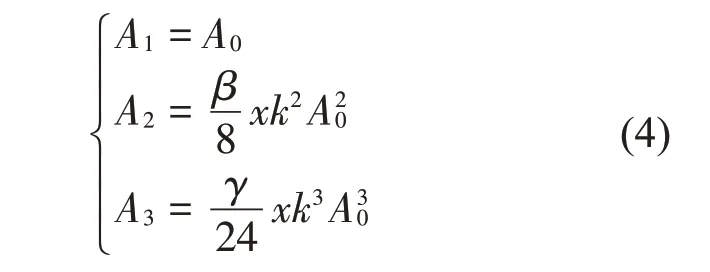
本文的主要目的是建立铝合金表面裂缝深度与超声非线性Lamb 波之间的对应关系。因为非线性Lamb 波的非线性效应对于三次谐波现象的产生极不明显，故重点推导二阶非线性系数。根据式（4）所示非线性波动方程得到非线性系数β与基波幅值A1和二次谐波幅值A2之间的关系式：

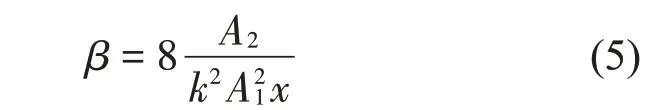
当材料属性、波数k和传播距离x确定时，β与成正比，引入相对非线性系数。

待测样品的非线性来源由两部分构成：一是金属材料固有的非线性，一是来源于金属近表面缺陷产生的声学非线性，因此可以建立非线性系数与缺陷深度之间的关系。

2 试验装置及结果分析

2.1 试验

本实验试件材料为6061铝合金和5A06-O铝合金，缺陷分为两种：（1）6060 铝合金尺寸为250 mm×100 mm×10 mm，在试件的中间位置沿宽度方向采用线切割的方法分别加工出深度为0mm、1mm、2 mm、3 mm、4 mm、5 mm且宽为0.1 mm人工裂缝，研究非线性系数与裂缝深度之间的关系；（2）5A06-O铝合金尺寸为300 mm×50 mm×2 mm，在试件的中间位置开一个三角形缺口，进行疲劳拉伸试验，振动周次为0、10 000、15 000、20 000 周次，形成宏观裂纹，观察不同疲劳周期对非线性效应的影响。

采用同侧超声激励接收方法。激励探头激发的超声信号沿着试件方向传播，经由接收探头后被接收，并采用角度可调探头以激发固定模态Lamb 波，其中选择的激励信号为汉宁窗调制的15个cycles单频正弦脉冲串。非线性系统检测原理图如图1所示，由RAM-5000-SNAP非线性高能超声测试系统、PC机、50 Ω负载、衰减器、高通和低通滤波器以及前置发大器组成。

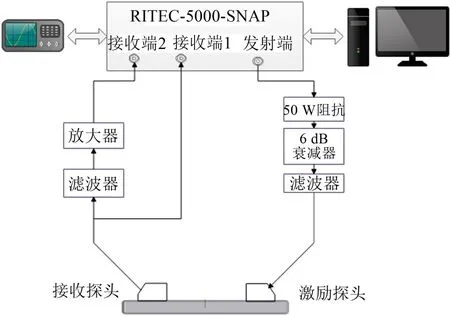
图1 试验装置示意图

2.2 实验结果分析

本实验所采用的非线性Lamb 波检测平台可以实现基波和二次谐波时域波形的接收，激励换能器中心频率为2.25 MHz，接收换能器中心频率为5 MHz。实验期间，基波和二次谐波幅值的测量条件应保持一致，对裂缝深度不同的试件和疲劳程度不同的10块试件依次进行基波和二次谐波的测量，对采集到的时域波形进行快速傅里叶变换（Fast Fourier Transform，FFT），该算法的最大优点是：不仅可以看到信号中包含哪些频率成分，还可以观察到频率成分的出现时间，且计算量小，变换后的基波振幅和二次谐波振幅如图2、图3、图4、图5所示。

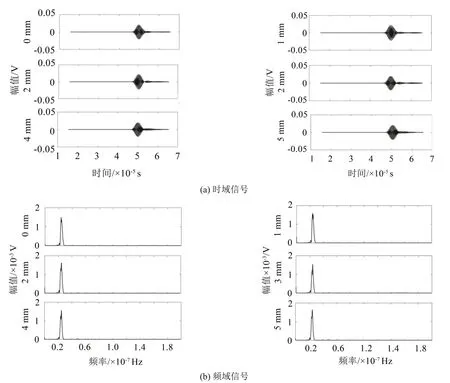
图2 人工裂纹试验的基波信号

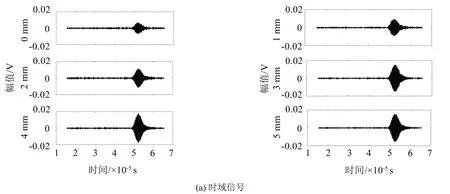
图3 人工裂纹测试二次谐波信号

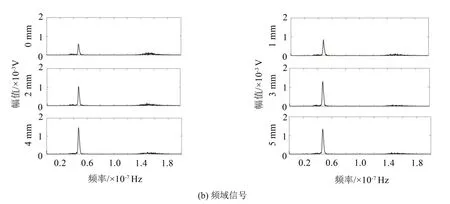
图3 人工裂纹测试二次谐波信号

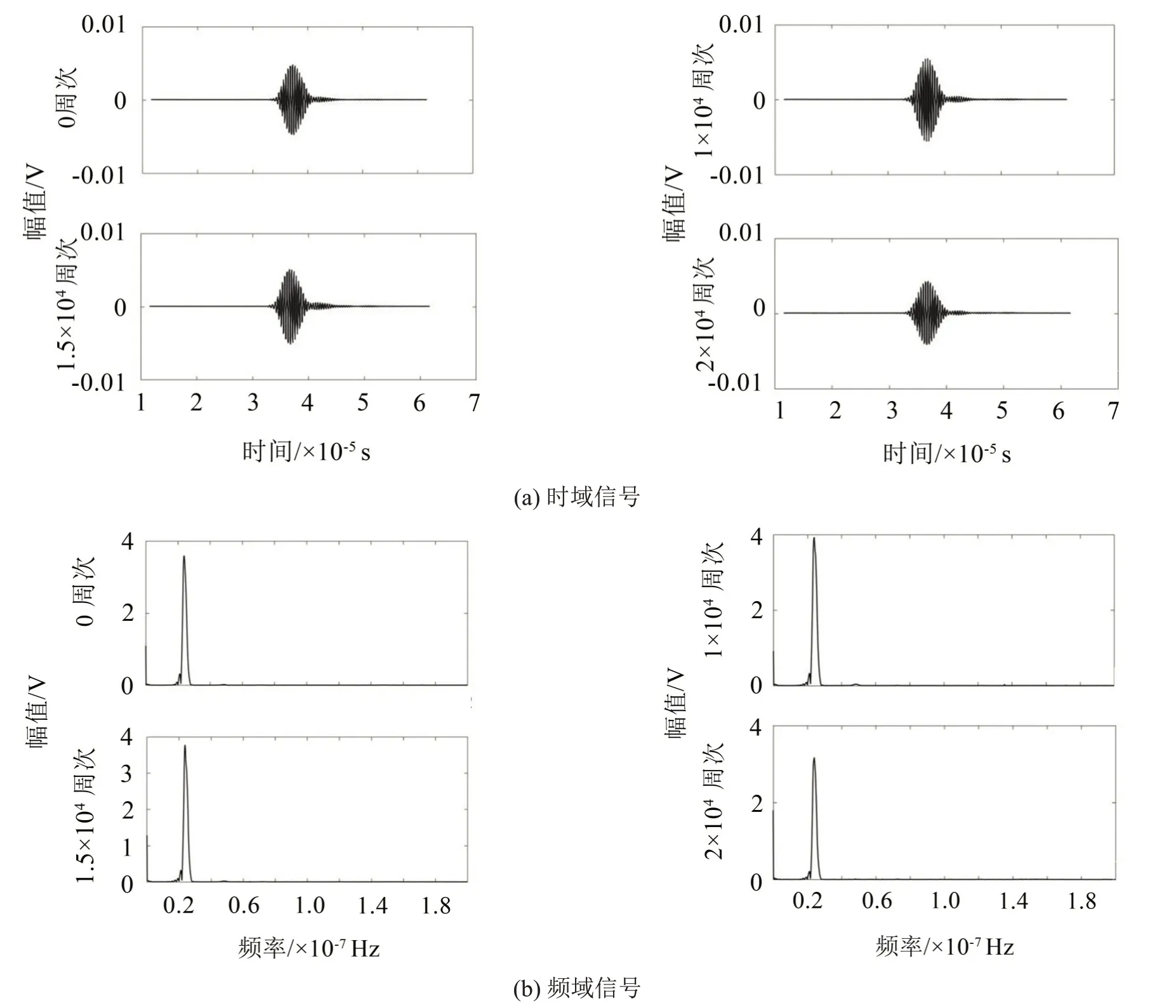
图4 疲劳裂纹试验基波信号

图2和图4分别显示了人工裂缝和疲劳裂纹的基波信号幅值，图3和图5分别显示了人工裂缝和疲劳裂纹的二次谐波信号幅值。从图2(b)和图4(b)中可以直观地看出，基波的幅值基本变化不大，而在图3(b)和图5(b)中，二次谐波的幅值对于缺陷损伤的大小比较敏感。因此，二次谐波幅值可以大致表征缺陷的深度，但是先前的非线性超声检测理论表明，相对超声非线性系数通常用于表征非线性效应，因为这是基波幅值和二次谐波幅值的综合性能的表现，能更好体现非线性效应的变化规律。将测量值代入式（6）得相对非线性系数β′，未处理试件的非线性相对系数为β′0。对线切割试件的相对非线性系数参数进行正则化处理，即所获得的合格相对非线性系数与缺陷试验片的缺陷尺寸之间的对应关系如图6、图7所示。

图5 疲劳裂纹试验二次谐波信号

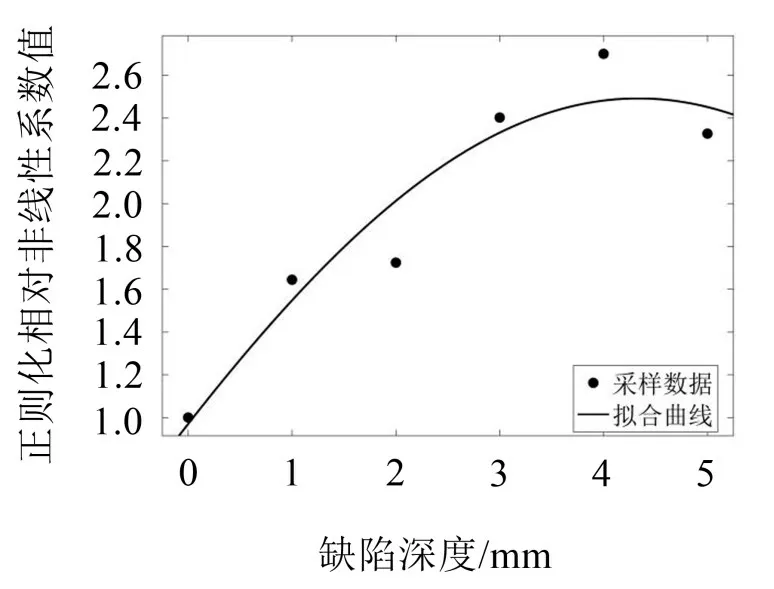
图6 正则化相对非线性系数与裂纹深度关系

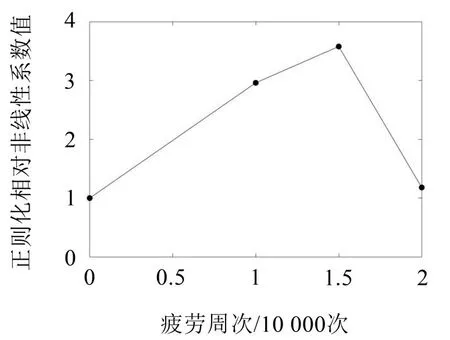
图7 正则化相对非线性系数与疲劳周次关系

从图6可以看出，该曲线可分为2个阶段：第1阶段在4 mm之前，正则化相对非线性随着裂纹深度的增加而增加；第2阶段为深度达到4 mm 后，超声非线性系数出现波动并呈下降趋势，表明随着缺陷深度的增加，相对非线性系数的变化并没有线性增加。这是因为lamb 波是在自由板中产生的平面应变波，其产生的频率与介质的厚度和激发波长的数量级相同，因此lamb 波对所检测薄板的结构敏感。因此，当金属板超过一定厚度时，lamb波的传播受到限制。

从图7可以看出，在试样整个裂纹扩展过程中，lamb 波非线性系数的变化趋势为：随着试样疲劳程度的增加，lamb波的相对非线性系数先增大后减小，前3个试件的数量依次增加，并且在第4个试件出现宏观裂纹后显示出下降的趋势，说明基于Lamb波的非线性超声检测对于疲劳损伤较为敏感，对于宏观裂纹的测量并不具有优势。

3 结语

（1）对采集到的两种缺陷对应的基波和二次谐波信号使用FFT进行分析、转换，可以有效观察接收信号随试件缺陷变化的幅值。

（2）通过分析对应不同深度缺陷的导波接收信号可知，缺陷深度在一定范围内与导波幅值之间具有较好的对应关系，Lamb波相对非线性系数能够很好地表征缺陷深度的大小，但是相对非线性系数并不随着裂纹深度的增加而线性增加，因此该方法只能应用于钣金件的近表面检测。

（3）在金属薄板疲劳裂纹加剧的过程中，裂纹产生的非线性效应随着疲劳程度的加深呈现增加趋势，但在试件疲劳断裂后呈下降趋势，说明材料的非线性效应主要由疲劳裂纹引起，此时的宏观裂纹对非线性效应影响不大。