非视距环境下基于二阶锥规划的RSS定位算法

金小萍，梁俊，谢少枫

（中国计量大学，浙江 杭州 310018）

1 引言

近年来，无线传感器网络（wireless sensor network，WSN）由于其低能耗和高效率，而在目标跟踪、室内定位、海上救援、森林火灾监测等领域得到了广泛的研究与应用。在WSN应用中，获取传感器节点的位置是必不可少的部分，关于节点位置确定的定位技术主要有如下两大类。

· 第一类：基于非测距的方法，如重心法、DV-HOP、APIT等方法[1-2]，这些方法虽然易于实施，成本较低，但定位精度受传感器网络布置的限制。

· 第二类：基于测距的定位方法，如RSS、AOA、TOA、TDOA等方法[3-5]，相比非测距方法，这些方法虽然需要额外的测距硬件，但定位精度更高，其中基于RSS的测距方法仅需要测出信号的衰减信息，且硬件实现成本相比其他测距方式也更低，在小规模传感器网络中，是一种高性价比的定位方式。然而基于RSS测距方式的定位精度易受非视距（non-line-of-sight，NLOS）环境的干扰，尤其是在障碍物密集的室内环境中，例如地下车库、监狱、医院等室内场景。在对人员进行定位时，墙壁、人流、房间的非视距干扰就很大，如果仍将传感器之间假设为视距（line-of-sight，LOS），则会导致RSS信息收集的不准确甚至RSS信息的丢失，最终造成较大的定位误差。

以往关于非视距环境下RSS定位问题的研究，主要包括3种类型。第一种方法基于非线性优化算法，参考文献[6]利用高斯混合模型将噪声项的非视距与视距分布变换为指数形式后再利用牛顿法进行求解。参考文献[7]基于最大似然（maximum likelihood，ML）准则构建了一个非线性方程组，合理设置初始点，再利用牛顿迭代法的思想进行求解。然而，此类方法需要对噪声误差以及非视距环境具有良好的认知，且非线性优化算法本身就存在估计误差较大的问题，定位精度无法保证。第二种方法基于加权最小二乘（weighted least squares，WLS）算法，此类方法的思想是将问题转化为线性的估计器再利用二分法进行求解。参考文献[8]使用无味变换（unscented transform，UT）将基于RSS的传感器定位问题转换为WLS估计问题应用于室内定位模型中，但该方法仍然需要对非视距状态具有良好的认知。参考文献[9]应用平方域（squared range，SR）和最小二乘（least squares，LS）准则将非视距偏差作为平衡干扰参数与目标位置一起进行估计，最终构建了一个WLS问题，但其中线性化的近似会带来额外的误差，从而导致求解精度不够准确。第三种方法基于凸优化技术，此类方法的思想是将非凸的定位问题转化为凸问题求解，参考文献[10]研究了RSS与TOA在非视距环境中的定位算法，对误差项进行一阶泰勒公式展开，在此基础上利用LS准则构建了定位问题，最终将原始的非凸问题转换为二阶锥规划（second-order cone programming，SOCP）问题，虽然此类方法可以有效地提高定位性能，但由于TOA定位对硬件要求较高，再结合RSS和TOA信息硬件设备的实现难度较大，并且将测距方程进行泰勒近似，会造成一定的误差。

基于上述背景，提出了一种基于SOCP的鲁棒性定位算法，与参考文献[6-10]不同，本文考虑在非视距干扰量的影响达到最大的情况下去处理非视距RSS定位问题。首先，利用对数乘法法则将RSS模型化为线性乘积形式，接着，采用最小平方相对误差（least squares relative error，LSRE）准则[12]构建了鲁棒性的节点定位方程，然后，利用凸优化技术提出了SOCP算法，从而解决原始定位问题的非凸性，最后，将问题推广到未知发射功率的情况，提出了迭代估计的SOCP算法。与以往的方法相比，所提算法不用识别非视距的状态以及分布，仅考虑非视距偏差达到最大的最坏情况，对非视距偏差具有鲁棒性，减轻了非视距偏差的影响，从而提升了定位性能。

2 非视距RSS系统模型及问题分析

考虑一个二维平面的无线传感器网络，该传感器网络具有N个锚节点si(i=1,…,n)，锚节点固定位置用来接收未知的待定位目标节点x的RSS信息，如图1所示，假定目标节点向锚节点发出信号，锚节点可以良好地从接收信号中提取RSS信息，在非视距环境下，对应着第i个锚节点的接收信号强度为[10-11]：其中，P0是参考距离处的发射功率（dBm），γ是路径损耗指数，d0是参考距离，设置为1 m，ni是测量的噪声误差量，一般设定服从零均值的高斯分布， 如ni～N(0,Oi2)。bi是非视距偏差（当bi=0的时候，i∈lLOS，当bi＞0，i∈lNLOS，其中lLOS与lNLOS分别代表视距传感器和非视距环境下的传感器的数目，对应的有lNLOS=N-lLOS），在本文中，假设非视距偏差的大小受一个已知常数bmax的限制， 如0 ≤bi≤bmax，·均表示二范数运算。

图1 RSS定位示意图

基于式（1）中的测量值Pi，可以得到关于未知节点x和bi(i=1,…,n)的最大似然估计：

式（2）的求解非常困难，由于未知的非视距偏差ib的存在，该问题的解是不确定的，需要去识别传感器节点之间的连接状态，才可以求解；其次，式（2）中的目标函数具有严重的非凸和非线性，难以获取全局最优解。为了解决这些问题，在第3节中，将通过假定非视距偏差的上界来构建鲁棒优化问题，以此克服非视距偏差的影响，并利用凸优化技术处理定位估计中求解量是非全局最优的问题。

3 鲁棒性SOCP定位算法

3.1 已知发射功率

首先，在发射功率已知（即0P已知）的情况下推导鲁棒性SOCP定位算法。针对式（1），在其两边同时加上变形移项后得到：

利用对数运算法则，将式（4）改写为线性乘积形式：

基于式（5）的乘积形式，得到如下关于未知节点x的鲁棒最小平方相对误差（robust least squares relative error，R-LSRE）估计表达式[12]：

该问题就是在最坏的情况下，对节点估计方程进行鲁棒优化，也就是最大化ie的情况下再最小化该目标函数。与参考文献[10]中利用LS估计构建的目标函数相比，LSRE估计比LS估计具有更好的估计精度[12]。此外，由于考虑了非视距干扰量的影响达到最大的最坏情况，对非视距偏差量具有鲁棒性，故利用该估计方法可以减轻非视距偏差带来的影响。

为了解决式（6），以ie为自变量，引入一个函数y=f(ei)，可以得到：

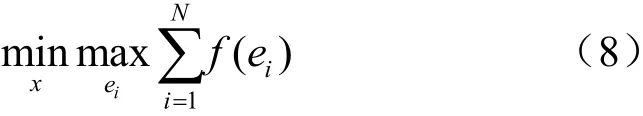
要解决式（8）对应的问题，需要计算函数算该问题，分为两种情况进行分析：

基于上述两种情况，式（8）可以等价为如下最优化目标节点问题：

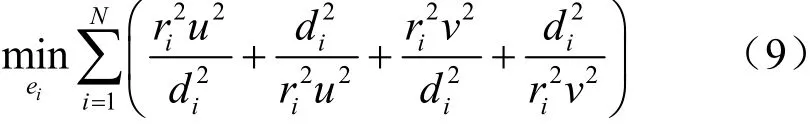
式（9）中最优化问题的目标函数是非凸非线性的。针对该问题，将利用凸优化松弛技术将原始节点估计问题转化为一个SOCP问题，首先，式（9）可以等价为如下上镜图形式问题[13]：

其中，t1i、t2i、t3i、t4i分别是所对应的约束条件的第i个变量的上界。

可以看出目标函数是线性的，而约束条件仍为非凸的。引入二个等价变量和基于此，把约束条件（10b）和引入的二个等价变量同时松弛到二阶锥（second-order cone，SOC）中，最终式（10）转变为[13]：

这是一个标准的SOCP问题，可以由内点法求解未知的目标节点，具体可由CVX仿真软件实现[14]，在后续描述中，将该发射功率已知的鲁棒性SOCP定位算法定义为R-SOCP。

3.2 未知发射功率

在实际情况下，传感器的发射功率0P往往随着外部环境的变化而发生改变，而这将造成额外的定位误差，针对这一情况，本节将在定位方法（11）的基础上进行改进，并通过一个迭代SOCP算法来提升性能。

当发射功率未知时, 等价于di参数未知。重新改写式（5），可以得到：

其中，对应参数n是未知量，类似地，可以得到如下最优化问题：

对于问题（13），其中的约束条件（13b）和（13c）是非凸的，因为其中的未知量在二阶锥约束中是非仿射非线性的。通过添加二阶锥松弛条件将发射功率量等价成伪线性形式，由此，式（13）可以二阶锥松弛（second-order cone relaxation，SOCR）为[13]：

式（14）也是一个SOCP问题，同样可由内点法求解，此外，为了进一步提升式（14）中SOCP方法的性能，提出了一个同时估计发射功率与目标位置的迭代SOCP算法，如算法1所示，后续把发射功率未知时的鲁棒性SOCP定位算法定义为R-SOCP-U，最终，将所推导的发射功率已知与发射功率未知情况下的鲁棒性SOCP定位算法归纳如下。

算法1鲁棒性SOCP定位算法

步骤1输入锚节点位置{si}；最大非视距偏差为{bmax}；噪声标准差为{σi}；路径损耗指数为{γ}；接收信号强度为{Pi}；发射功率为{P0}；最大迭代次数为{kmax}；极小正值为{}δ；

步骤2当发射功率已知，求解式（11），得到估计的目标位置；当发射功率未知，求解式（14），得到估计位置xk1-，令k=1；

步骤3将xk1-代入式（1）中，反解出发射功率pk-1：

步骤4利用Pk-1求解式（11），得到估计位置xk；

步骤5判断如果＜δ或者k＞kmax则得到估计的目标位置，如果不是，则令k=k+1，重新计算步骤3。

输出步骤2或步骤5的目标节点的位置x。

4 定位性能仿真

在定位性能仿真中，主要选择了3种方法用来对比R-SOCP与R-SOCP-U算法：基于牛顿迭代思路的NR法[7]、基于WLS的UT法[8]、基于LS的SOCP法[10]。其中，SOCP等凸问题可使用CVX软件包进行仿真，并且仿真中只涉及RSS算法的部分。定位环境设定如下：所有传感器均匀设定在30 m×30 m的平面区域，其中的仿真参数设定如下：发射功率P0=-4 0 dBm ，路径损耗指数γ=4。简单起见，假设RSS测量模型的所有噪声标准差都相等，也就是σi=σ。定位的性能采用均方根误差（root mean square error, RMSE）进行分析，定义如下：

其中，Mc是蒙特卡罗仿真次数，本次仿真，进行运算3 000次，ix为第i次不同定位算法运算所产生的估计位置，ex为每次实验当中随机产生的目标节点的真实位置。

图2展示了R-SOCP算法的RMSE与噪声标准差σ之间的关系的性能比较图形，设定噪声标准差从1 dB到6 dB均匀地增加。如图2中显示，所有算法的RMSE都随着σ的增长而变大，这是因为随着环境中的噪声干扰增加，传感器接收的信号会受到较大的干扰，从而造成误差。最后，图2显示，对于所有考虑到的σ跨度，所提出的R-SOCP算法的定位误差是最小的，优于现有的算法。

图2 RMSE随着噪声标准差变化

图3展示了R-SOCP算法的RMSE与锚节点数目N之间的关系的性能比较图形，设定σ= 3 dB，lNLOS=N，bmax= 6 dB ，锚节点数目从4到10均匀增加。可以看出，随着N的增加，所有算法的RMSE都会变得更小。这是因为随着锚节点数量的增加，目标节点可以从锚节点处获取更多的信号信息，从而提高定位精度。此外，当布置的锚节点传感器多于8个的时候，所有算法的RMSE将趋于平稳，这是因为当N很大时，在网络中收集的RSS信息足以使所有算法的性能达到最好。最后，图3显示，与其他算法相比，随着N的增加，所提出的算法的RMSE也是最低的，例如，当N=10时，R-SOCP算法的RMSE=3.4 m，相比SOCP、UT和NR算法的性能分别提高了0.7 m、2.1 m、3.3 m。

图3 RMSE随着锚节点数目变化

图4展示了R-SOCP算法的RMSE与非视距锚节点数目lNLOS之间的关系的性能比较曲线，设定σ=3 dB，N=8，bmax= 6 dB ，锚节点中非视距传感器的数目lNLOS从2个一直增加到8个。可以看到，R-SOCP算法的RMSE始终要低于SOCP、UT和NR算法，其定位误差是最小的。此外，基于牛顿迭代思路的NR法和线性近似的UT法会随着非视距传感器数目的增多而降低定位性能，因为其不能良好地识别非视距传感器。而所提出的R-SOCP和SOCP算法都显示了对非视距偏差的良好缓解能力，其定位性能不会随着传感器网络中的非视距锚节点数目而改变，其中R-SOCP算法由于考虑了非视距偏差达到最大的最坏情况下非视距传感器的误差干扰，不用再去识别非视距传感器，对非视距偏差具有鲁棒性，从而减轻了非视距偏差的影响，带来了性能上的提升。

图4 RMSE随着非视距锚节点数目变化

图5展示了R-SOCP算法的RMSE与最大非视偏差bmax之间关系的性能比较曲线，设定σ= 1dB ，N=lNLOS=10，最大非视距偏差bmax从1 dB到6 dB均匀增加。可以看出，所有考虑的算法的RMSE都会随着bmax的增长而变大。这是因为非视距环境越恶劣，RSS信号的接收也会受到很大干扰，从而造成误差。此外，对于所有考虑的最大非视距偏差，本文所提算法都要优于其余的算法，最后，R-SOCP相比其他算法，性能分别提升了1 m、2.5 m、3.6 m。

图5 RMSE随着最大非视距偏差变化

图6展示了未知发射功率下的R-SOCP-U算法的累积分布函数（cumulative distribution function，CDF）性能对比曲线，设定bmax=6 dB，可以看出在未知发射功率下的R-SOCP-U算法的性能相比于SOCP算法以及UT算法都要好，具体而言，当估计误差为2 m时，R-SOCP-U算法的累积分布函数为95%，SOCP算法的累积分布函数为86%，UT算法的累积分布函数为58%，也就是说在3 000次蒙特卡罗仿真运算中、95%的情况下，R-SOCP-U算法的估计误差维持在2 m之内，可以得知，R-SOCP-U算法的定位精度是良好的。

图6 R-SOCP-U算法CDF曲线的性能对比

5 复杂度分析

对于所提出的鲁棒性SOCP定位算法，其中SOCP问题是由内点法去求解[13]，其中内点法中每次的迭代复杂度为O(N3)，每次的迭代数目为ξ为设定的SOCP问题求解的精度，综上可知，整体的运算复杂度为而求解NR法的牛顿迭代法解法的迭代次数设定为kmax，求解UT法的二分法解法设定最大迭代次数为kmax，它们的最差运算复杂度均为O(kmaxN)。可以看出所提鲁棒性SOCP定位算法的运算复杂度与SOCP算法一致，但高于NR法与UT算法，权衡复杂度与定位精度，其性能是较好的。

6 结束语

针对非视距环境下的RSS定位，本文提出了鲁棒性SOCP定位算法，该算法在假设非视距偏差上界的基础上，无须获取非视距偏差在实际环境中的统计信息和数目等情况，有效抑制了非视距偏差对定位性能造成的干扰。同时，将该算法推广到未知发射功率的情况，提出了改进的迭代SOCP算法，通过将发射功率与目标位置同时迭代估计来提高定位性能。仿真结果表明，所提出的鲁棒性SOCP定位算法对非视距偏差具有鲁棒性，减轻了非视距偏差的影响，与现有的RSS非视距定位方法相比，也具有更好的定位精度。最后，本文所提出的基于SOCP的定位算法虽然定位精度较高，但存在运算复杂度较高的问题，在之后的研究中，将重点解决复杂度较高的问题。