一种降低复杂度的压缩感知水声信道估计方法

于玄，耿烜

（上海海事大学信息工程学院，上海 201306）

1 引言

水声（underwater acoustic，UWA）通信技术与水下机器人、无人驾驶船舶或水下传感器网络相结合，在海洋探测、军事监视等方面发挥着重要作用，因此发展水声通信技术具有重要的现实意义[1]。然而，由于水声信道多径干扰强烈、信道响应稳定性差[2-4]，水声通信系统存在剧烈的码间干扰，给水声通信带来了极大的困难和挑战。在水声通信系统中，接收机无法准确获取信道响应值，需要对其进行估计，信道估计在时变UWA信道中起着重要的作用。

海洋声信道，尤其是在中短距离的高速水声通信中，水声信道呈很长的时延扩展，信号能量集中在几个显著的抽头上，信道响应具有明显的稀疏特性，这种现象经常发生在浅海[5-6]。传统的水声信道估计方法是非稀疏信道估计，如最小均方误差（minimum mean square error，MMSE）信道估计算法[7]，它没有利用水声信道稀疏特性的先验信息，估计得到的稀疏多径信道的脉冲响应抽头系数会有大量的非零值，降低了估计精度。近年，利用水声通信信道的时域稀疏特性和匹配跟踪的思想，压缩感知（compressed sensing，CS）[8]方法可以准确地重构信号，有效地抑制噪声对信道估计的干扰。因此，在UWA通信系统中，基于压缩感知的稀疏信道估计获得了研究者的关注[9]。在压缩感知算法中，贪婪重构算法是一类低复杂度、收敛速度快和易于实现的重构算法[10]。其中，正交匹配跟踪（orthogonal matching pursuit，OMP）[11]和子空间追踪（subspace pursuit，SP）[12]是常用的贪婪重构算法。然而，OMP算法每次只选择一个原子，如果错误选择了任意一个原子，则不能正确恢复，重建概率低。SP算法在每次搜索中添加和删除原子，比OMP降低了复杂度，但不能保证更新支撑集时对应残差的收敛性。参考文献[13]提出了一种前向回溯正交匹配追踪（look-ahead backtracking orthogonal matching pursuit，LABOMP）算法，采用前向预测添加新原子，并利用回溯策略剔除最不可靠的原子，以平衡精度和随机扰动，相对于OMP和SP，能够更为准确地重建水声信道，但计算复杂度较高。

针对上述问题，本文提出了一种降低复杂度的前向回溯正交匹配追踪（reduced-complexity look-ahead backtracking orthogonal matching pursuit，RC-LABOMP）水声信道估计算法。该算法在LABOMP方法的基础上，首先计算正交匹配追踪（OMP）和子空间追踪（SP）估计的支撑集，然后将两类支撑集的交集和并集作为算法的先验信息，利用先验信息进行预处理，最后基于LABOMP的触发回溯对信道进行估计，得到水声信道的时域冲激响应。该算法改变了原LABOMP算法中支撑集的初始化值和原子的索引范围，减少了算法的迭代次数，同时缩小了原子的索引范围，因而降低了原LABOMP的计算复杂度。此外，本文将提出的信道估计算法应用于水声迭代Turbo均衡[14]中，将信道估计值作为参数输入Turbo均衡器中，在随后的迭代中，译码器反馈的软信息作为特殊的训练序列，用于信道估计，形成信道估计和Turbo均衡的迭代反馈环，用以提高系统的整体性能。仿真结果表明，与传统的信道估计方法相比，提出的RC-LABOMP算法具有估计精度高、误码率低的优点，并且与LAMBOMP算法相比，计算效率得到了显著提高。

2 系统模型

2.1 传输模型

包含信道估计和Turbo均衡的水声通信系统模型如图1所示。在发送端，对长度为L的信息比特序列an进行编码，输出长度为2(L+2)的信息位序列bn，经交织cn和调制映射得到数据符号序列sn，发送信号xn由sn与训练符号tn复用而生成，其中训练符号tn是接收机已知的，并且用于信道估计处理。xn经过水声信道hn传输，到达接收端，接收信号yn为：

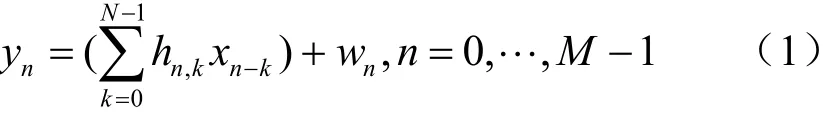
其中，nx、yn、nw分别表示在n时刻离散的发送信号，接收信号和均值为0、方差为2σ的高斯白噪声，hn,k表示n时刻、时延为k的水声信道冲激响应，N为信道长度，M是观测窗口长度。

在接收端，单输入单输出（single-input single-output，SISO）均衡模块将接收信号yn、先验信息以及信道估计提供的信道作为输入，输出符号外部信息经解交织处理输出的软信息作为译码器的输入。SISO译码器输出发射符号的估计值解码后的后验信息经交织处理得到对数似然比（log likelihood ratio，LLR）进行判决作为新的训练序列。然后信道估计器利用新的训练和yn得到信道估计值ˆnh，作为均衡器的输入。不断进行上述迭代过程，直到译码器性能收敛。

2.2 稀疏信道模型

假设在n时刻水声信道的时域冲激响应为：

其中，iα和iτ分别表示第i径的幅度和时延，N为多径的数目，K为非零多径的数目。因此，长度为N的水声信道只有K个抽头系数是非0的，稀疏度为K。

由训练序列组成M×N的矩阵A，定义为信道估计需要的观测矩阵，具体构成为：根据式（1）在n时刻的输入输出关系，观测矩阵A经过信道后的观测向量yh为：

其中，wh为M×1观测噪声向量，h为N×1稀疏信道冲激响应，稀疏度为K，K＜M，且M＜N。接收端根据已知的观测矩阵A，使用压缩感知信道估计算法获得h的估计值。

3 提出的信道估计算法

3.1 压缩感知信道估计基本原理

CS的核心思想是将压缩与采样合并进行。为了保证观测信号在压缩的过程中重要信息不会被破坏，能够正确恢复出原始信号，A必须满足约束等距性质，如式（5）所示：

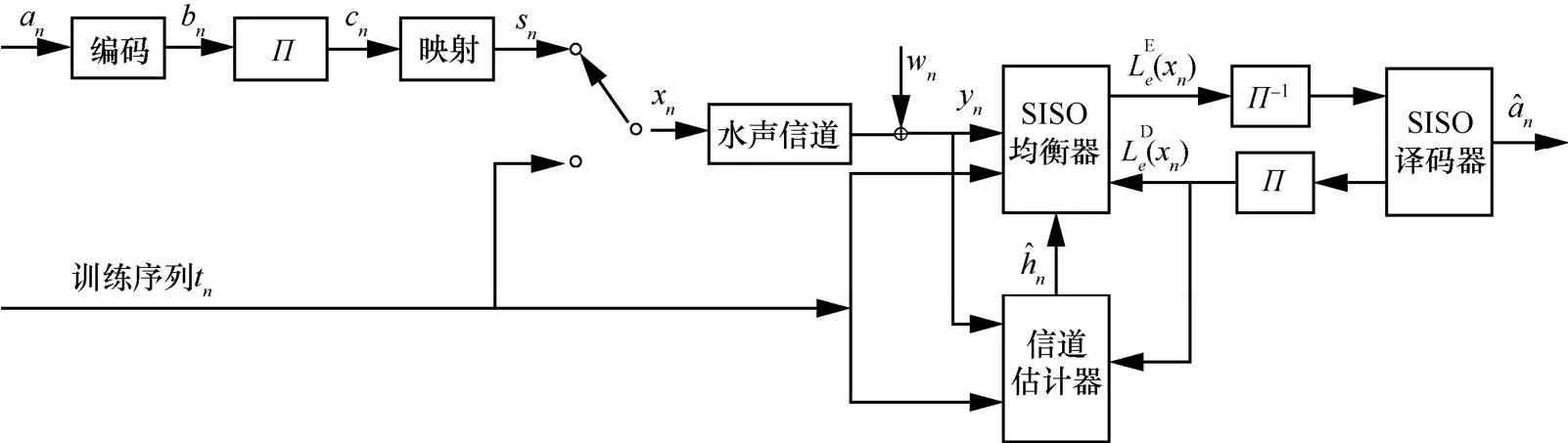
图1 包含信道估计和Turbo均衡的水声通信系统模型

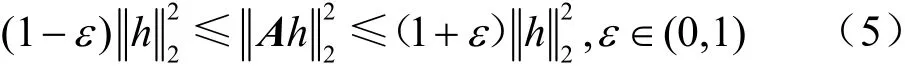
接收端已知观测向量yh和观测矩阵A，根据欠定方程yh=Ah求解得到h，由于h无法直接从观测值计算得到，因此，求解目标转变为该方程组所有解中，最稀疏的h值，即CS压缩信号恢复值。h的求解可转换为式（6）最优化问题进行求解：

本文中信号的重构是指观测矩阵A从M维观测向量yh中重构N维h的过程；原子是指观测矩阵A中的每一个列向量；支撑集存放原子对应索引的集合；残差表示观测向量yh与模型输出结果Ah的差值。

OMP、SP和本文提出的RC-LABOMP算法属于CS中的贪婪算法，包含两个步骤：原子选择和信号估计。首先初始化稀疏向量为零，然后根据已知的观测矩阵A和观测向量yh，利用A中的原子与信号残差的相关性，每次迭代选取一个或多个与残差最匹配的原子，将原子对应的索引逐次存入支撑集，然后根据支撑集，通过求yh=Ah的最小二乘解[15]进行信号估计，得到估计值ˆh。

3.2 OMP和SP算法

OMP算法[11]的基本思想是在每次迭代中，选取与残差最匹配的原子，把原子的索引存储起来，构成支撑集JOMP,k，根据支撑集对应的原子，更新矩阵AJOMP,k，并估计出信道冲激响应，多次迭代后算法收敛获得最终的信道估计值。在第k次迭代时，首先计算残差rk-1与观测矩阵A各个原子的内积rk-1,Aj，然后选择内积最大值所对应的A的列索引序号χk，存入支撑集JOMP,k中，即JOMP,k=JOMP,k-1∪χk，如式（7）所示：

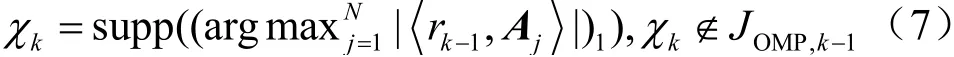
其中，符号supp(·)表示选取内积最大JOMP,k值对应的A列向量的索引。接着，根据支撑集的值，获得矩阵AJOMP,k，使用最小二乘法求解第k次迭代的信道估计值，如式（8）所示：

根据信道估计值，更新残差值kr，如（9）所示：

最后，迭代式（7）～式（9），当算法达到收敛条件时，获得最终的信道估计值。

SP算法[12]是对OMP算法的一种改进，OMP算法每次迭代时选取一个索引值放入支撑集，与之不同的是，SP算法在每次迭代时，选取前K个与残差最匹配的原子的索引并入支撑集，然后通过回溯检验的方法剔除不可靠的原子。在第k次迭代时，求得残差rk1-与观测矩阵A各个原子的内积，根据式（10）选择前K个最大值对应A的列索引序号γk，逐次存入作为支撑集：

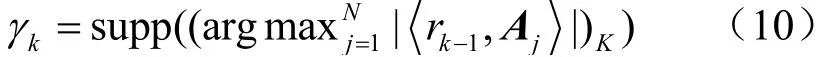
3.3 提出的RC-LABOMP算法

原始的LABOMP[13]算法中的支撑集从空集开始，选择与残差具有最大内积的前ζ个原子，并进行前向预测，通过重复调用这一过程，向支撑集里不断地添加原子对应的索引。该方法需要迭代稀疏度K次才能准确获取信道，使得能源成本非常高。因此，本文提出了一种降低复杂度的前向回溯正交匹配追踪（RC-LABOMP）算法，该算法在LABOMP算法的基础上，提出将OMP和SP估计支撑集的交集和并集作为先验信息处理，用以降低原算法的迭代次数。

在初始化时，首先根据第3.2节的方法获得OMP和SP算法的支撑集JOMP和JSP，然后根据式（11）和式（12）分别得到：

其中，λ表示JOMP和JSP的交集，用来作为RC-LABOMP算法的支撑集初始化值，ϖ表示JOMP和JSP的并集，其元素作为观测矩阵A的索引列序号。经过以上预处理，RC-LABOMP算法初始化支撑集J0、迭代次数k、估计信道值和索引序号π~分别由式（13）～式（15）所示：

式（13）中，card()λ表示集合中元素的个数。式（14）中，表示不含支撑集λ的元素对应的信道估计值。经过式（13）～式（15）的预处理后，RC-LABOMP初始从card()λ开始迭代，直到迭代到稀疏度K次。在第k次迭代中，利用式（15）求得残差rk-1与观测矩阵A的第j列的内积（jϖ∈），选择前ζ（ζ称为前向参数）个最大值A的列索引序号π~，然后基于LABOMP的前向预测，依次预测这ζ个原子对迭代残差的影响，返回残差二范数lη中最小的原子的索引d，并将dπ~加入支撑集Jk中。当大多数正确原子对应的索引被选入候选集时，即迭代次数大于初始化设定的常数阈值φ时，触发回溯，以剔除不可靠的原子。在后续迭代中，每次迭代前向预测时，添加一个新原子，每两次迭代触发回溯时，剔除一个错误原子，并向候选集添加一个原子的索引序号，并且不断更新残差kr和信道冲激响应hˆJk，直到满足终止条件。其具体实现过程如下。

步骤1首先利用OMP和SP算法的支撑集JOMP和JSP进行预处理，得到

步骤2初始化估计信道为残 差 为支 撑 集 为迭代次数为前向参数为ζ= ceil(K/2)，回溯阈值为φ= 0.8×K。

步骤3计算相关系数

步骤4l从1到ζ进行前向预测，每次返回残 差 二 范 数中 间 支 撑 集 为残差Rq=yh-AI AI-1yh,q= card(I)，从q+1次开始，迭代到K次。对于第p次迭代，首先更新相关系数更新中间支撑集最后更新残差

步骤5找到残差二范数中最小的原子的索引并将加入支撑集中，更新估计信道值

步骤6回溯策略，剔除不可靠的原子。当满足条件时，不可靠的原子位置为从支撑集Jk中剔除，支撑集为

步骤7更新残差和信道分别为

步骤8若k＞K，终止迭代。否则，k=k+1，重复步骤3进入下一次迭代。

原LABOMP算法是一种贪婪算法，以空集作为初始支撑集，从0开始进行逐次迭代到稀疏度K次，迭代次数为K，具有较高的计算复杂度。而本文提出的RC-LABOMP算法，利用OMP和SP算法支撑集的交集λ，作为RC-LABOMP的初始支撑集，这是因为两种算法已经选择了和残差最相关的原子，这些原子具有很高的准确度，将这些原子对应的支撑集交集作为RC-LABOMP的支撑集初始值，将使RC-LABOMP从card()λ开始迭代，而不是从0开始迭代，因此显著降低了原LABOMP的迭代次数。另一方面，在迭代计算时，原LABOMP算法对A的每个原子与残差计算内积，选择出具有最大内积的ζ个原子，而RC-LABOMP算法利用OMP和SP算法支撑集并集ϖ所对应的原子与残差进行内积。因此，通过以上两步处理，本文提出的RC-LABOMP算法能够从减少迭代次数和缩小原子索引范围两个方面，同时降低LABOMP算法的计算复杂度。

3.4 提出的RC-LABOMP算法复杂度

分析RC-LABOMP计算复杂度，主要考虑加法和乘法运算。在RC-LABOMP算法中，RC-LABOMP使用了OMP[8]和SP[9]算法作为先验信息，OMP和SP算法复杂度分别为O(K(MN+KM))和O((MN+KM)logK)。匹配滤波器需要MN标准乘法，最小二乘法的每个信号估计都需要O(KM)乘法[12]。RC-LABOMP外部迭代次数为K-card(λ)，加上追踪回溯可以看成迭代次数为2(K-card(λ))-φ次迭代。在前向预测中，匹配滤波会花费φ)2)的乘积，在回溯中，总共包含(K- card(λ)-φ)个最小二乘法估计。因此，综合考虑以上因素，RC-LABOMP的计算复杂度为

4 结合RC-LABOMP的Turbo均衡实现

Turbo均衡广泛应用于水声通信物理层解码中，本文根据Turbo均衡的特点，将提出的RC-LABOMP算法应用在近似线性MMSE的频域Turbo均衡[16]中，从而提高系统的整体误码率性能。图2为结合RC-LABOMP的Turbo均衡结构。

图2中，基于近似线性MMSE的频域Turbo均衡模块由FFT、MMSE频域均衡、IFFT、映射和解映射5个模块构成。其中，输入信号为发送端接收信号yn，RC-LABOMP估计的信道和先验信息，输出信号为外部信息，经过解交织，译码器重新交织，反馈得到先验信息进行硬判决处理，并将判断结果作为RC-LABOMP估计器的输入，从而使信道估计和Turbo均衡构成反馈迭代处理结构。具体实现步骤总结如下。

图2 结合RC-LABOMP的Turbo均衡结构

步骤1首先利用tn的信息，RC-LABOMP算法进行信道估计，得到初始信道估计值

步骤2近似线性MMSE的频域Turbo均衡器将作为信道参数，计算第一次的外部信息值通过解交织、MAP译码器再交织，得到反馈的先验信息

步骤3进行硬判决处理，将判决信息作为新的训练序列输入RC-LABOMP中进行信道估计，得到后续符号的信道估计值

步骤4近似线性MMSE的频域Turbo均衡器将作为信道参数，计算后续的外部信息值通过解交织，MAP译码器再交织，得到

步骤5判断是否达到迭代次数，若达到迭代次数，则进行判决得到译码输出，否则，重复步骤3。

随着迭代次数的增加，MAP译码器反馈的软信息会更加准确，RC-LABOMP估计的ˆnh也更准确，从而使迭代结果更精确。当迭代次数达到一定值时，MAP译码器反馈的软信息趋于稳定，对信道估计值变化较小，从而迭代系统趋于稳定。

5 实验结果及分析

通过Monte Carlo（蒙特卡洛）仿真，本文分析了提出的RC-LABOMP算法在不同信道条件下的性能，并与基于非稀疏信道估计MMSE方法、稀疏信道估计OMP算法、SP算法和LABOMP算法进行了比较。

系统设置有效符号帧长度为1 024，选用1/2码率的卷积码进行信道编码，调制方式为QPSK，加性高斯白噪声作为背景噪声，观测窗口长度为15，使用随机交织进行交织/解交织器，使用MATLAB软件对算法的CPU运行时间进行了测试，作为计算复杂度的比较。

5.1 随机信道下性能比较

本文首先仿真了随机稀疏信道下的算法性能，其中稀疏信道的脉冲响应由计算机随机产生，信道长度为62，稀疏度为6，随机分配非零元素位置。在每种情况下，蒙特卡洛试验大于500次。

在稀疏时变信道中，图3显示了在信噪比为10 dB的条件下，不同信道估计算法估计出的信道进行Turbo频域均衡后的星座图。从图3中可以看出，基于压缩感知理论的OMP、SP、LABOMP和RC-LABOMP算法，均衡后的星座图点，比MMSE算法更为集中，因此更适用于稀疏信道。

图3 不同信道估计方法对应的均衡后的星座图

图4和图5分别给出了在不同信噪比（SNR）下，几种信道估计算法结合Turbo均衡的均方误差（MSE）和误码率（BER）性能比较，其中Turbo均衡迭代次数设置为3。从图4中可以看出，随着信噪比的增加，MMSE、OMP、SP、LABOMP和RC-LABOMP的MSE性能都呈下降趋势，但是MMSE信道估计方法的MSE值最大，RC-LABOMP和LABOMP的MSE值最小，并且RC-LABOMP可以获得接近于LABOMP的MSE性能，而SP和OMP的性能居于MMSE和LABOMP算法之间。

图4 随机信道下不同算法的信道估计均方误差比较

图5 随机信道下不同算法的误码率比较

从图5中可以看出，信道估计的BER值均随着信噪比的增加而降低，与MSE的性能相似，MMSE算法的误码率性能最差，RC-LABOMP和LABOMP算法的误码率性能始终优于OMP和SP算法。

5.2 水声信道下性能比较

本文接着仿真了水声信道条件下的算法性能。使用参考文献[17]在松花湖测得的数据，根据Bellhop算法绘制声速剖面曲线，如图6所示，其中水深50 m，换能器深度为25 m，水听器离水面的深度为25 m，水平传播距离2 km。

图7显示了在稀疏时变水声信道条件下，不同算法估计每个数据块的初始信道冲激响应。如图7所示，MMSE估计的脉冲响应抽头系数会有大量的非零值，并不适用于稀疏信道估计。当实际的信道抽头不存在时，OMP和SP有时会估计得到幅度很小的信道抽头，而LABOMP与RC-LABOMP具有更为精确的信道冲激响应估计能力，当实际信道抽头不存在时，两种算法不会估计信道抽头系数。

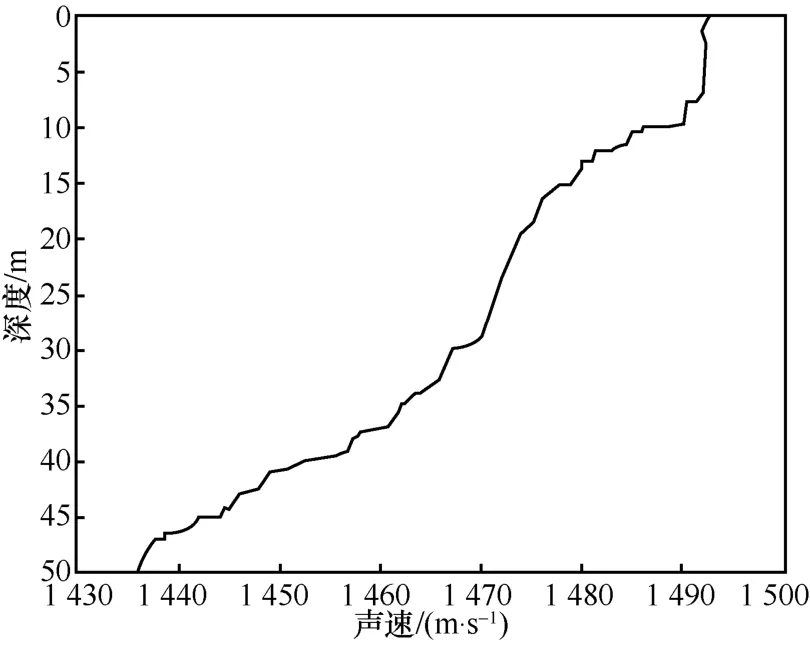
图6 基于松花湖数据的声速剖面

图7 不同信道估计算法得到的初始信道冲激响应

图8和图9分别给出了在水声信道条件下，不同信噪比（SNR）时，不同信道估计算法结合Turbo均衡的MSE和BER性能比较。从图8、图9中可以看出，MMSE算法在水声信道中性能依然表现最差，而RC-LABOMP和LABOMP算法性能最好，其余两种算法居中，与随机信道条件下的性能表现一致。

5.3 复杂度比较

图8 水声信道下不同算法的信道估计均方误差比较

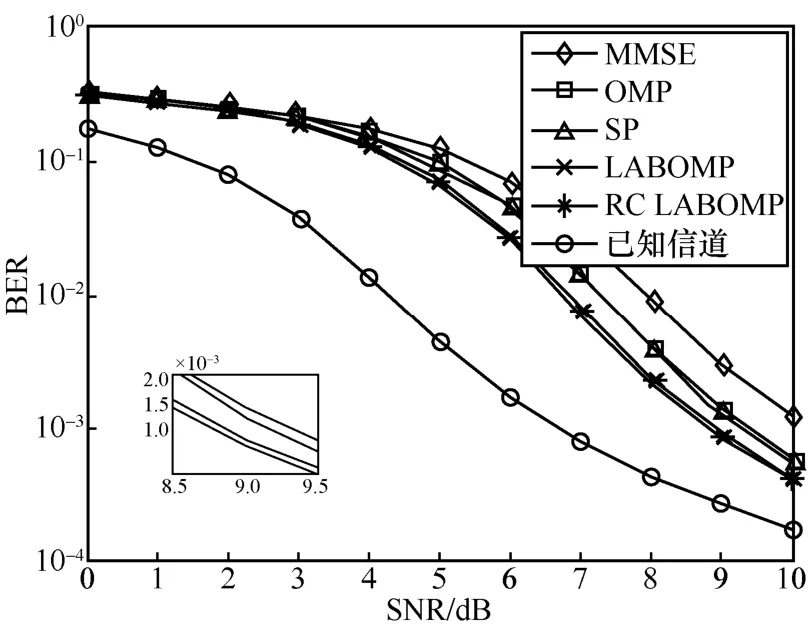
图9 水声信道下不同算法的误码率比较

接着进行了仿真实验对比。本文分别使用仿真程序的平均迭代次数，原子的索引范围和运行时间来衡量不同算法的复杂度。其中，仿真设信道长度为100，随机生成一系列稀疏度不同的信道冲激响应。在信噪比为3 dB和Turbo均衡迭代次数为3的情况下，分别对LABOMP和RC-LABOMP算法的复杂度进行比较。

图10（a）和图10（b）分别显示了两种算法运行500次的平均迭代次数和原子的索引范围。如图10（a）所示，LABOMP的迭代次数近似为稀疏度，而RC-LABOMP的迭代次数始终低于LABOMP的迭代次数。原LABOMP算法从0开始进行逐次迭代到稀疏度K次，迭代次数为K。因此，随着稀疏度K不断增大，迭代次数不断变大。RC-LABOMP迭代次数为K-card(λ)，根据K和card(λ)的变化分析，当稀疏度为5～25时，card(λ)的变化速度始终小于K的变化速度，即K-card(λ)的值将增加；当稀疏度大于25时，card(λ)变化速度始终大于K的变化速度，K-card(λ)的值将减小。因此，当K＞25时，图10（a）RC-LABOMP的曲线随着稀疏度增加而变小。当稀疏度为25时，RC-LABOMP比LABOMP的迭代次数平均减少52%。图10（b）中，LABOMP的原子索引范围始终为观测矩阵的所有原子，而RC-LABOMP的索引范围虽然呈增长趋势，但整体明显低于LABOMP的索引范围；当稀疏度为40时，RC-LABOMP比LABOMP的索引范围平均缩小52%。

图10 算法随信道稀疏度变化的迭代次数和搜索原子范围

图11 不同算法随信道稀疏度变化的程序运行时间

图11比较了4种压缩感知信道估计算法运行500次的平均程序运行时间，图11中RC-LABOMP包含了OMP和SP算法预处理的时间。如图11所示，随着稀疏度变大，4种算法的运行时间也都逐渐变大，但是RC-LABOMP的运行时间始终低于LABOMP。当信道稀疏度不断增大时，由于RC-LABOMP迭代的次数会变小，因此其运行时间趋于平稳，而原LABOMP始终迭代K次，其运行时间依然呈上升趋势。当稀疏度为40时，RC-LABOMP比LABOMP的运行时间平均节省了约93%。

需要指出的是，根据图4、图5和图11的结果分析，SP算法性能虽然劣于LABOMP算法，但是复杂度也显著降低。与SP算法相比，原LABOMP和本文提出的RC-LABOMP算法在Turbo均衡系统中，在提高复杂度的同时，并未获得显著的性能增益。但在参考文献[18]的分析和仿真指出，LABOMP算法在水声TDS-OFDM系统中，可以获得十分显著的性能提高，因此，笔者将在下一步研究工作中进一步验证RC-LABOMP算法在其他水声通信系统中的性能。

最后，本文仿真了信道长度为100、稀疏度为11的实时稀疏时变水声信道条件下的复杂度比较。在信噪比为3 dB和Turbo均衡迭代次数为3的情况下运行500次，表1为LABOMP和RC-LABOMP的平均迭代次数和原子的索引范围，表2为不同算法所需的平均运行时间。从表1和表2中可以看出，RC-LABOMP在水声信道条件下，计算复杂度和程序运行时间依然明显低于LABOMP算法，与随机信道条件下的复杂度性能表现一致。

6 结束语

本文提出了一种降低复杂度的前向回溯正交匹配追踪水声信道估计算法，并将该算法应用于水声迭代Turbo均衡中。该算法以OMP和SP所估计的支撑集的交集和并集作为预处理条件，从而减少迭代次数和缩小原子的索引范围，降低原LABOMP的计算复杂度，并能保持原有的性能。给出了随机稀疏信道和浅海水声信道下的水下通信实验结果，同MMSE、OMP和SP信道估计算法相比，所提出的RC-LABOMP算法能够提升估计精度和误码率性能；与LABOMP算法相比，提出的算法能够在获得近似于LABOMP的性能前提下，显著降低算法的计算复杂度和运行时间，提升了水声通信的收敛性能。此外，所提出的降低复杂度信道估计算法不仅可以适用于本文研究的浅海场景，也可以应用到信道呈稀疏性的复杂的空中无线通信场景，在下一步研究工作中进一步验证RC-LABOMP算法在其他场景中的性能。

表1 LABOMP和RC-LABOMP算法的平均迭代次数和搜索原子范围比较

表2 不同算法的平均运行时间比较