开口圆环类声子晶体传播禁带特性研究
唐荣江,潘朝远,郑伟光,何宏斌,唐经添
(桂林电子科技大学机电工程学院,桂林 541004)
0 引 言
声子晶体是一种周期性排列的复合结构,它一般由两种及以上的材料构成,该结构具有抑制或衰减波传播的禁带特性,已广泛应用于噪声振动控制领域[1-2]。研究人员通过结构的创新设计来获得带隙,并聚焦于声子晶体带隙内传输损耗性能的研究。Elford[3]和Yu[4]等设计了一种开口圆环结构,均能获得宽禁带和性能优越的衰减损耗。但频率局限在高频,这显然不利于这一类结构的实际应用。为满足低频段的减振需求,姜久龙等[5]设计了一种双开口的Helmholtz周期结构,在100 Hz附近得到一条窄带隙,但其衰减损耗仍集中在2 000 Hz的中高频。梁孝东等[6]则提出一种四组元的声子晶体结构,强的衰减损耗都表现在200 Hz以下的禁带内,这对缓解地铁的低频振动十分有利。以上的研究并不重视晶胞对称性的问题,较多地关注晶体禁带单一方向上的衰减能力[2-6]。这对非严格对称的声子晶体而言,并不能全面反映结构的声学性能。有研究表明:打破模型的对称性有利于改善某些频率的隔声效果[7];芯体和基体的对称性不同,带隙表现差异明显[8-9]。
因此,本文对非严格对称的开口圆环类声子晶体结构进行振动带隙研究。基于有限元法和弹性波传播理论分析其禁带特性;通过施加振动激励,比较晶体MΓ和ΓX方向的衰减曲线,发现在禁带内ΓX比MΓ方向的衰减能力强。禁带内弹性波传播被明显抑制,结构产生的位移变形量很小,通带内则相反,这一结果全面展现了非严格对称结构的隔振性能。本文借助振动模态解释了带隙产生的原因,并对影响带隙的几何尺寸和材料参数进行深入研究。
1 模型与弹性波传播理论
1.1 单个晶胞模型
本文设计的二维声子晶体如图1(a)所示。晶格常数a=10 mm,圆环半径r1=2.5 mm和r2=4 mm,开槽宽度w=1 mm。中心开槽圆环称为芯体或散射体,材料为结构钢,将其嵌入橡胶基体中研究其传输损耗性能,材料参数见表1。图1(b)则表示正方晶格的布里渊区,由ΓXM围成的三角形区域为第一布里渊区或不可约布里渊区(irreducible Brillouin zone,简称IBZ),由于本模型非严格对称,需对ΓXMR区域进行全扫略。图1(c)展示了波矢k的计算域和ΓXM的扫略方向。

图1 晶胞结构和不可约布里渊区

表1 材料参数
1.2 弹性波传播理论
对晶胞的边界使用Bloch定理[10],计算单个晶胞的振动模式来预测无限周期系统的能带结构:
u(r)=us(r,k)e-ikr
(1)
式中:u(r)是位移矢量,r是区域Ω内的位置矢量,us(r,k)是布里渊区的周期函数,k=[kx,ky]T是波矢,弹性波在无限周期介质中传播的动态平衡方程为[11]:
(2)

(3)
us(r+R)-us(r)=0
(4)
式(4)中R是晶胞的平移周期[13];有限元晶胞剖分网格后,离散形式的特征方程为
(K(k)-ω2M)u(r)=0
(5)
式中,K(k)和M表示元胞波矢k的刚度矩阵和质量矩阵[11],具体定义如式(6)所示,此处的ω2是方程的特征值。
(6)

(7)
式中,λ和μ是材料的拉梅(lame)常数,拉梅常数和杨氏模量E、泊松比υ又存在以下关系:
(8)
因此,将材料属性代入(7),(8)两式再结合频率值,即可得到弹性波长与结构带隙的关系。
2 带隙结构与传输特性分析
本文采取先从M→Γ开始扫掠,拾取前十阶能带结构。计算MΓ方向时,波矢k在x,y方向的分量kx,ky在0到π/a间同时取25个数值点,从而得到一组能带曲线;计算ΓX方向时,使波矢k在y方向的分量ky=0,而kx从0到π/a间取25个数值点,得到另一组能带曲线;计算XM方向时,保持波矢k在x方向的分量kx=π/a不变,使ky从0到π/a间取25个数值点,计算得第三组能带曲线;其余两组方法相同,将得到的五组能带曲线结合起来便能获得该结构的禁带。能带结构图如图2(a)所示。而对于传输损耗,在结构边界通过给定单位加速度激励Ii并获得出口处加速度幅值大小It,并由(9)式计算得出。
TL=-20log(Ii/It)
(9)
将晶胞沿x轴阵列5个并施加ΓX和MΓ方向Ii=1 m/s2的加速度激励,计算频域下的声子晶体传输特性,如图2(b)所示。
由图2(a)可见在716.1~1 012.5 Hz频率范围内有300 Hz宽的完整禁带,方向带隙有三条:分别是在600 Hz附近的MΓ方向和频率为1 405~1 522 Hz的ΓX、RΓ方向。禁带内的传输损耗表现优异,方向禁带只表现比较小的衰减峰值。值得注意的是MΓ和ΓX方向衰减性能并不同步,其中水平的ΓX方向最稳定,峰值均出现在相应带隙内,而MΓ方向比较异常,在禁带内825 Hz出现衰减低谷。为此选取了几个处于衰减曲线峰值(波峰波谷)点的位移云图做分析,如图3所示。
图3(a)~(f)对应图2(b)中A~F各点。显然,在选取的通带频率为425 Hz和1 015 Hz的弹性波均能顺利通过,特别是1 015 Hz时,声子晶体本身的振动加剧了位移振幅。在禁带825 Hz内,两个晶胞周围的橡胶产生振动导致MΓ方向出现衰减低谷,原因是晶胞非严格对称导致弹性波沿5×5的晶体边缘传播(见图3(b)),加速度信号通过结构边缘传递过去,增加晶体数量能改善这一缺陷;而ΓX方向可以完美抑制或衰减弹性波,位移只在激励源一侧产生,振动响应未能穿过声子晶体,所以ΓX方向衰减表现更好。究其原因,由于开口的存在,使得该结构只有沿y轴方向的对称性,弹性波在MΓ方向传播时晶胞的周期性抑制作用减弱。在禁带725 ~1 000 Hz内ΓX方向平均衰减量为27.8 dB,MΓ方向为22.3 dB,同比增加5.5 dB。此外,700 Hz和1 525 Hz的方向带隙衰减弹性波的性能也比较好,衰减量为26.4 dB和14.3 dB。更进一步地,该带隙的打开和属于哪种机理下的声子晶体仍值得继续探索。
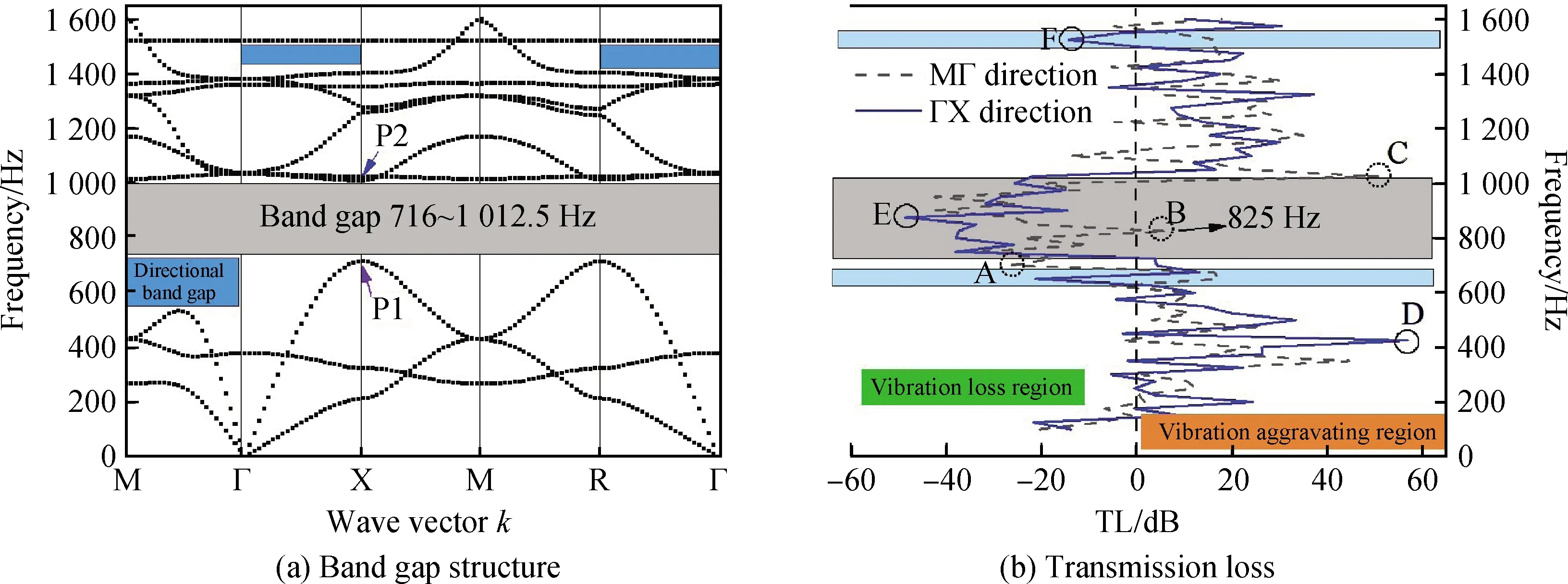
图2 声子晶体能带结构(a)和传输特性(b)

图3 通带和禁带的位移云图
图4比较了相等波矢值下起始和截止频率处晶胞的振动模态,它们分别对应由钢块和橡胶基体组成的“质量-弹簧”系统的平移和扭转振动模式。在P1点芯体受到左侧边角橡胶的挤压从而发生水平向右的平移运动,与垂直传来的弹性波刚好存在一个相位差,同频率的弹性波与该晶体结构振动反相进而抑制了波传播,禁带起始频率得以打开;到P2点橡胶从晶胞斜对角以相反的方向垂直运动,会对芯体产生一个剪切作用力,导致芯体发生扭转振动,橡胶板基体中的长波行波难以与圆环钢的振动相耦合[6]。此外,由于芯体及其附属的橡胶未能把振动能量局限在单元内[14],与同相弹性波不存在耦合作用,禁带在P2点截止。
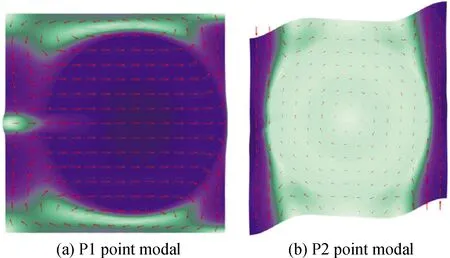
图4 P点振动模态图
将结构钢的材料参数代入(7),(8)两式,取晶格常数a=10 mm带隙中心频率为800 Hz作为比较波长,得到纵波波长约为7.3 m,横波波长约为112.8 m,两者与晶格尺寸存在2~4个数量级的差异,这类结构突破了布拉格机理的限制[15]。
3 模型讨论
局域共振机理认为即使芯体随机分布,在特定频率的弹性波激励下,芯体产生共振能获得禁带。但如何设计芯体结构以及在基体中的分配特性是问题的关键。因此本节先对芯体的结构和分布进行探索,然后分析芯体材料对带隙的影响,最后综合讨论了禁带与晶格常数、开槽宽度等参数的关系。由图2(a)可见,扫略IBZ即可反映这类结构的带隙曲线,相比于扫略BZ能节省计算时间,因此下文只对M→Γ→X→M进行扫略。
3.1 改变芯体结构
由前面的分析可知,带隙的起始频率由芯体的平移运动出现的频率决定,而截止频率则取决于芯体的旋转运动。因此,可通过芯体结构的设计来增加系统的振动模态,利用其振动模态耦合来产生低频的带隙。具体做法是:在芯体内部增加一个钢环来提高振子的刚度,当其平移运动时惯性力变大,以此来提升抑制弹性波传播的性能;另一个模型则是水平位置再开一槽,削弱其刚度作为比较。
由图5(a)可知,增加一个同心圆环(内r=1 mm外r=1.5 mm)后,起始频率为674 Hz,比之前降低了42 Hz,但是第一禁带被第四能带分割分成两部分,分别为674.2~893.9 Hz和896.7~1 012.1 Hz,很可能是内外振子的旋转模态的相互耦合导致的[7]。图5(b)表明再开一个槽后,前十阶能带降低到1 400 Hz以下并且没有完整禁带出现,只有部分方向带隙。可以发现,通过结构的略微调整即可改变其固有频率,使结构出现了一些消极的耦合作用,造成通带的产生。

图5 芯体结构对带隙的影响
3.2 改变芯体材料
为了明确材料属性对禁带特性的影响,改变芯体或基体材料参数保持另一对象其他参数不变,分别统计第一带隙的起始、截止频率和带隙宽度,模型仍采用第1.1节所述。
将芯体从结构钢分别替换为铜、铅和钨材料,发现结构钢和铜材料带隙频率变化不大,而铅和钨芯体材料造成起始频率降低,特别是以钨为芯体的起始频率和带隙宽度均达到500 Hz,如图6所示。参考表1的材料属性参数可以发现,增大材料的密度有利于获得低频带隙。

图6 芯体材料对带隙的影响
3.3 改变几何尺寸参数
几何参数包括内环半径r1、晶格常数a和开槽宽度w,而改变内环半径r1时将直接导致芯体的填充率变化。
由图7(a)可见,当内环半径r1从2 mm增大3.5 mm时(芯体的填充率相应减小),发现第一带隙截止频率基本不变而起始频率增大导致带隙宽度变窄;而增大橡胶基体的晶格常数时起始和截止频率均降低,当晶格常数a大于30 mm时,在400 Hz以内就能获得完整禁带,特别是a=40 mm时起始频率为179 Hz截止频率为253 Hz(见图7(b));而当开槽宽度变宽时,起始频率不变而截止频率降低导致带宽变窄。综合来看,填充率影响起始频率而开槽宽度影响截止频率,晶格常数对带隙起始和截止频率均有影响;通过增大晶格尺寸和芯体填充率能获得频率较低的宽频禁带。

图7 参数对带隙的影响
4 结 论
本文设计了一种非严格对称的开口圆环类局域共振声子晶体结构,首先分析了其带隙特性并比较了各方向的振动衰减性能;然后通过振动模态解释了带隙产生的原因;最后对芯体结构、几何尺寸和材料参数进行研究,得到结论如下:
(1)该声子晶体在716.1~1 012.5 Hz频率范围内有300 Hz宽的完整禁带,禁带内ΓX方向传输损耗平均值比MΓ方向提高5.5 dB,原因是晶胞非严格对称导致弹性波沿5×5的晶体边缘传播。
(2)带隙的打开和截止是由芯体的平移运动和旋转运动决定,芯体结构能明显改变系统的固有频率从而改变振动模态。
(3)在选取的4种金属材料中,以钨为芯体的能得到起始频率和带宽均为500 Hz的优越带隙。
(4)芯体填充率影响起始频率而开槽宽度影响截止频率,通过增大晶格尺寸、填充率和材料密度能获得低频宽禁带。
综上,由于开口圆环的非严格对称性,ΓX方向传输损耗性能优于MΓ方向;在相应材料组合下能获得起始和带隙宽均为500 Hz的低频带隙;增大芯体的材料密度、填充率和晶格尺寸有助于获得较低频率的完整带隙。

