基于主成分分析和凸优化的低压配电网拓扑识别方法

冯人海，赵 政，谢 生，黄建理，王 威

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 天津大学微电子学院，天津 300072；3. 南方电网科学研究院有限责任公司，广州 510670)；4. 国网天津市电力公司城南供电分公司，天津 300201)

随着科学技术的进步，配电网的建设得到了快速发展，其规模和复杂性也日益增加．低压配电网作为电力系统的重要组成部分，对社会生活的影响最为直接．低压配电网拓扑信息是数据系统计算、停电范围控制和负荷传递分析的基础，基于正确的低压配电网拓扑结构，可以产生精确的状态监测数据和智能仪表数据[1-3]．由于低压配电网的拓扑结构会因设备更新、修复和维护而发生改变，通常电网运营商不能及时获得拓扑结构的变化信息，这会给电网公司的运营带来不便[4]，因此快速获取准确的低压配电网拓扑信息具有重要的现实意义．

近年来，我国积极推动智能电网技术研发与应用工作[5-6]．智能电表作为其中的关键组成部分，已经得到了全面的普及．结合微能量收集的智能电表具有强大的数据收集能力和信息交互能力[7-9]，因此基于结合微能量收集的智能电表测量数据的低压配电网拓扑识别问题是一项极具潜力的研究课题．

国内外学者们基于不同的测量数据和原理进行了大量尝试，其中一些方法是基于时间序列的电压测量数据来推断相位连通性和配电网拓扑结构．文献[10]使用电压相位测量装置对配电网拓扑结构进行识别，但这种方法增加了设备成本，不便于对拥有大量节点的低压配电网进行操作．文献[11]将相关性作为最佳信号检测的衡量标准，从智能电表电压测量数据中确定用户的相位连接．文献[12]采用邻近算法求解用户台区归属问题，但此算法得出的结果会受用户地理位置的影响而导致无法实现准确识别．随着智能电表的普及，产生了基于智能电表测量数据的拓扑识别方法．文献[13-14]基于智能电表数据角度对网络拓扑结构进行了理论解释，利用主成分分析(principal component analysis，PCA)算法对低压配电网拓扑结构进行识别，该方法简单易行，求解速度快，但识别准确率较低．文献[15-16]应用所提出的线性优化算法来识别相位连接和拓扑结构，但随着数据矩阵规模的增加，算法空间复杂度和时间复杂度会急剧增加．文献[17-19]采用粒子群等仿生算法对优化模型进行求解，优点在于方便求解多目标优化问题，缺点是容易陷入局部最优，且搜索速度较慢．

为解决低压配电网拓扑结构的识别问题，本文提出了一种基于主成分分析和凸优化理论的低压配电网拓扑识别方法．该方法首先分析了低压配电网的典型结构，建立了低压配电网拓扑分析模型；基于智能电表实时数据和电能守恒原理建立了多元线性回归的数学模型；利用主成分分析对数据集矩阵进行降维压缩，保留了数据集的主要信息；利用范数逼近原理和凸松弛将低压配电网拓扑识别问题转化为可解的凸优化问题，并利用 cvx 工具箱进行求解．通过对低压配电网算例的仿真，验证了算法的可行性和高效性．所提出的算法具有如下优点：

(1) 本算法避免了其他传统优化算法容易陷入局部解的问题，求得的解为全局最优解；

(2) 利用 PCA 对数据集矩阵进行处理，保留了原始数据间的本质信息，拓扑识别仿真运行时间受电量测量采样点数的影响为微秒级；

(3) 将拓扑求解问题通过范数逼近和凸松弛转换为凸优化求解问题，与文献[14]中的 PCA 算法相比，拓扑识别准确率更高．

1 低压配电网拓扑识别系统建模

低压配电网是指10 kV/400 V 台区公变变压器以下的网络结构，10 kV 中压母线经过台区变压器后降为 400 V 低压母线，400 V 低压母线经若干出线柜分成多条400 V 分支馈线，通过各400 V 分支馈线将电能分配至不同的楼宇单元，各分支馈线再通过若干分支箱或低压母线将电能送至各终端用户[20]．低压配电网的拓扑结构可以被认为是安装在变电站、馈线、变压器和用户之间的连接．低电压配电网的节点可以根据电压水平被分成不同层，同层节点具有相同的电压水平．相邻层之间的连接关系是唯一的．基于电压水平的低压配电网拓扑结构如图1 所示，黑色节点为末端节点，为配电网的终端用户，红色节点为母节点，向下连接着子节点．

设有a 个终端用户连接到b 个配电变压器．以瓦特每小时(W/h)为单位按 15 min 的时间间隔对智能电表进行采样．义为在第j 个时间间隔上采集的 N (N = a +b )个节点的样本，如式(1)所示．

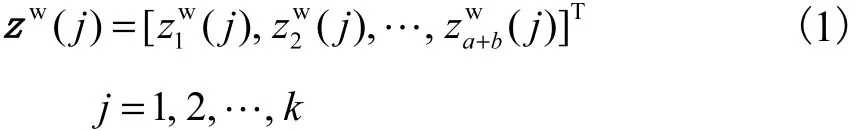
通常，测量值会受到随机噪声的干扰而导致测量值存在误差．测量值的数据向量如式(2)所示．

电能守恒原理表明，在任何时间间隔内，某配电变压器上的电能消耗量等于连接到该变压器上的所有用户的电能消耗量之和[21]．根据这一原理，所有终端用户的测量值与上层所有配电变压器的测量值之间的线性关系可以用式(4)表示．

2 拓扑结构识别算法

2.1 主成分分析

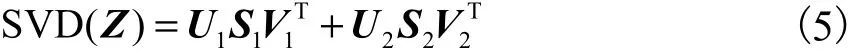
式中：U1是对应于a 个最大特征值的正交特征向量的集合；中b 个最小特征值的正交特征向量的集合；的奇异值对角矩阵．设是C 延展出的子空间，则满足式(6)所示关系．

回归模型可以通过将变量划分为a 维的自变量zi和b 维的 zd来获得．以按如下方式划别是 a ×a和 a ×b 维矩阵[14]，则有式(7)所示结论．

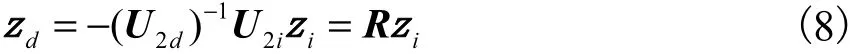
2.2 凸优化求解拓扑矩阵

凸优化问题即在一组等式或不等式约束下，求函数的最小值(或最大值)，其一般表示形式为

式中： m∈ U； n∈ T ．

考虑到每个终端用户只能连接到某一个配电变压器上，即连接关系是唯一的，这决定了拓扑回归矩阵R 的行向量只有一个元素是 1，其他元素为 0，这种关系可以用式(12)表示．

式中A 是元素全为1 的行向量，长度为a．

本文的拓扑识别问题可以表示为多个约束下的优化问题，如式(13)所示．

因0-1 规划问题的可行域不是连续的，不符合凸集的定义，需松弛为不等式约束问题．将式(13)中的模型转化为凸优化模型，如式(14)所示．

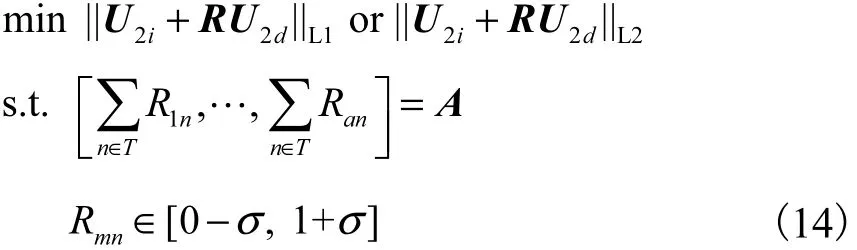
式中σ 是松弛变量．

因 L1 范数和 L2 范数均为凸函数，因此凸松弛后的模型同样为凸函数，而且其目标函数易求偏导，采用内点法可以快速求解得到最优解[22]．

3 拓扑识别算法

3.1 相位识别

相位识别系统中的节点可分为相线节点和用户节点．相位识别问题是确定相线节点和用户节点的连接关系．将相线节点的数据集变量作为因变量，用户节点的数据集变量作为自变量，基于能量守恒原理得到相线节点和用户节点间的线性回归关系．

相位识别算法的流程分为PCA 数据处理和凸优化建模计算两个阶段．

步骤1 PCA 数据处理．

步骤2 凸优化建模计算．

(1) 设定求解变量R．

(2) 设定目标函数：

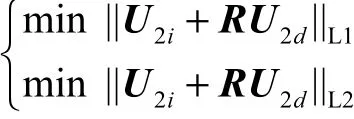
(3) 设定约束条件：

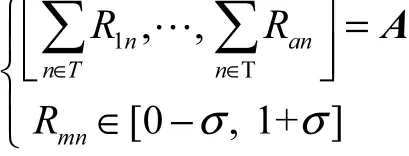
(5) R 每行中最接近 1 的元素被舍入为 1，其余为0，通过R 推断相位连通性．

3.2 低压配电网完整拓扑结构识别算法

通过相位识别算法既可以计算出任何相邻电压层节点的拓扑结构，也可以计算出不同电压层的拓扑结构．将两层识别算法扩展，可以实现低压配电网完整拓扑结构的识别．

假设低压配电网共有Q 层相同电压水平的结构，把不同层从下到上进行编号．相邻两层的拓扑矩阵可由本文提出的凸优化算法进行求解，通过推断所有相邻电压层节点之间的连通性，可以识别出完整的低压配电网拓扑结构．算法步骤如下．

步骤 2 执行相位识别算法原理中的步骤 1、步骤2，得到矩．

步骤3 q = q+ 1，转步骤1，直到 q = Q- 1，通过断完整的低压配电网拓扑结构．

4 仿真分析

4.1 相位识别

首先通过相位识别算例来验证所提出算法的可行性，算例由终端用户节点和相线节点组成．考虑一个具有 12 个节点的相位连接网络，该网络有 9 个用户节点连接到3 条不同的相线，设定0.5σ =．用户和相线节点在各个时间间隔采集到的电量测量值如表1 所示．

将步骤 1、步骤 2 应用于数据集，计算相位拓扑矩阵，结果如表2 所示．

结合相位拓扑矩阵和式(1)的定义，可以得出用户和相线的连通关系，可视化连接关系如图 2 所示：用户节点5、6 和8 与相线节点A 相连；用户节点1、3、4 和 9 与相线节点 B 相连；用户节点 2 和 7 与相线节点C 相连．

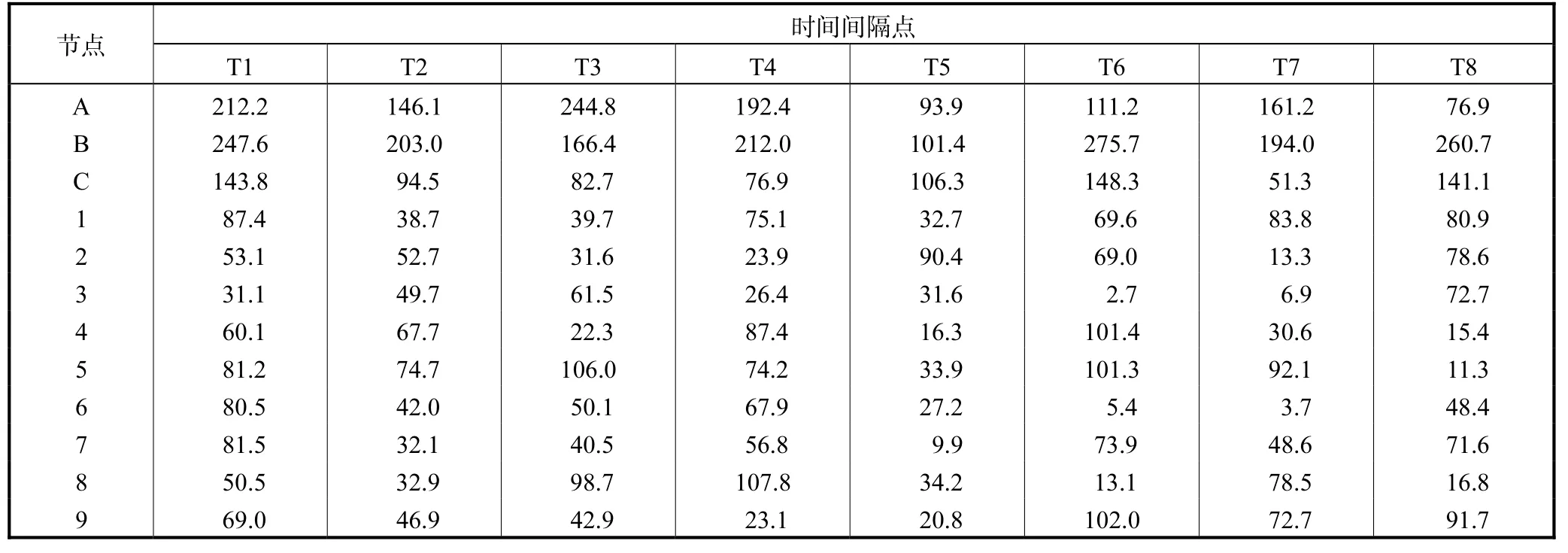
表1 相位网络的电量测量数据Tab.1 Energy measurement data of phase network

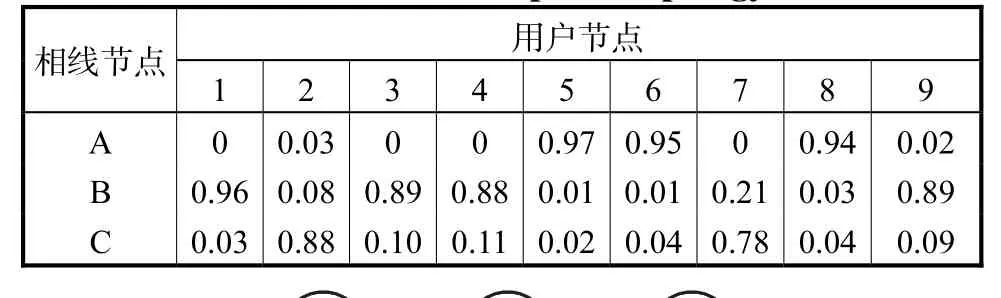
表2 相位拓扑矩阵Tab.2 Matrix of phase topology

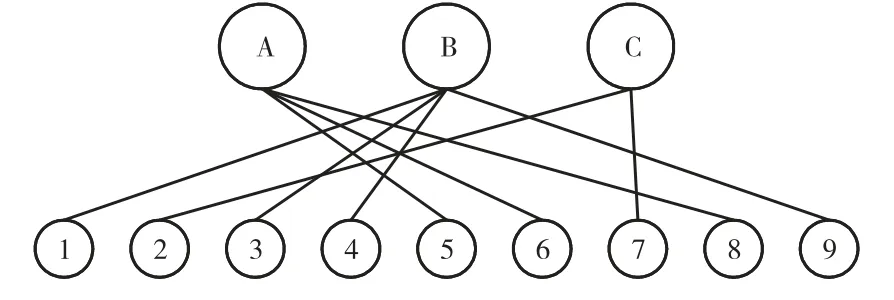
图2 相位连接关系Fig.2 Phase connection relationship

4.2 大型低压配电网拓扑识别仿真分析

接下来在大型低压配电网上验证了本文提出的拓扑识别算法．该网络使用 Matlab 中的随机数生成器构建，为方便计算，设某一区域有 100 个用户连接到 4 个台区，连接关系未知；每个节点电表的读数是从随机均匀分布中取样的，平均值和最大值等于用户的平均负荷和峰值负荷．

本文使用不同的数据集进行仿真实验．用k 值分别为0～300 的电量测量值进行网络拓扑识别仿真实验．将仿真实验输出的最优解矩阵与实际的网络拓扑拓扑矩阵进行比较，重复仿真实验 200 次．拓扑识别的准确率定义为正确识别出连接关系的节点数占总节点数的百分比．

(1) 无噪声仿真：在这种情况下，分别进行了基于PCA 的L1 范数优化和L2 范数优化的仿真实验，并与文献[15]中的 PCA 算法进行对比，结果如图 3所示．可以看出，与文献[15]中的 PCA 算法相比，基于 PCA 的范数优化算法在拓扑准确率上表现更好，但3 种算法要达到100%的拓扑识别准确率需要的时间采样点数量是相差无几的．单从优化算法对比，目标函数的 L2 范数的识别准确率在整体上都是优于L1 范数的．因此在采样数据不足的情况下可以使用目标函数的 L2 范数优化算法，以得到更准确的拓扑结构．

图3 无噪声的拓扑识别准确率Fig.3 Success rate of topology identification without noise

(2) 有噪声仿真：因信噪比为20 dB 的高斯噪声更接近现实测量数据中噪声的统计特性[15]，所以引入了信噪比为20 dB 的高斯随机噪声，仿真结果如图4 所示．可以看出，与文献[15]中的 PCA 算法相比，本文提出的算法在识别准确率达到100%时所需的时间采样点数从248 降低到200，意味着在现实中可以节省大量的采样时间．

图4 有噪声的拓扑识别准确率Fig.4 Success rate of topology identification with noise

如在采样数据充足的情况下使拓扑识别准确率达到 100%，可以选用算法运行时间复杂度表现更好的算法．

4.3 算法运行时间复杂度分析

随着智能电网云计算对数据处理的速度要求越来越高，算法的时间复杂度成为衡量拓扑识别算法优劣的重要指标．算法的时间复杂度可以由算法中时间花销最大的步骤来决定，步骤 1 运行时间是微秒级[13]，而步骤 2 运行时间为秒级，因此以步骤2 为主分析本文算法的时间复杂度．拓扑识别算法的仿真时间主要取决于数据集矩阵的规模，即取决于配电网节点数N 和数据采样点数k．

首先分析配电网节点数N 对算法运行时间的影响．固定数据采样点数k，将本文算法应用于N 值不同的数据集进行仿真．设，重复实验 200次，得到算法的仿真时间结果，如图5 所示．

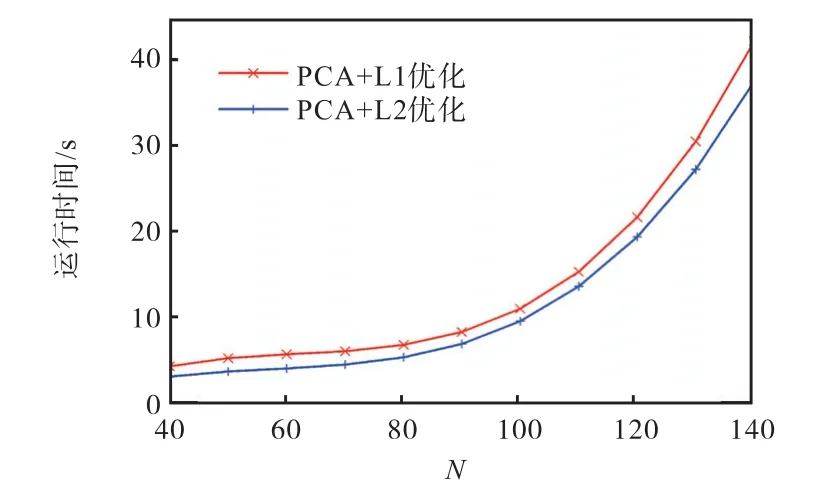
图5 固定k 的仿真时间对比Fig.5 Simulation time comparison under fixed k

从图 5 可以看出，基于 PCA 的优化时间是呈多项式型增加的．从优化算法比较，目标函数的 L2 范数仿真时间在整体上是优于 L1 范数的．扩展到拥有大量节点低压配电网，可以估算出拓扑识别所用的时间．

考虑到实际配电网中相邻层的节点数一般是固定的，因此在仿真中固定了配电网节点数N ( a = 1 00,b = 4)，通过增加k 值来观察仿真时间．算法的运行时间结果如图6 所示．

从图6 可以看出，本文提出的算法的运行时间随着k 值的增大没有产生较大的变化，说明算法的运行时间已被固定在一个区间内．其微小的上升是因步骤1 仿真时间的增加，而步骤2 计算所需的数据集已被降维到与k 值无关，因此可以得出，本文提出的算法的时间复杂度为 O ( N2)．

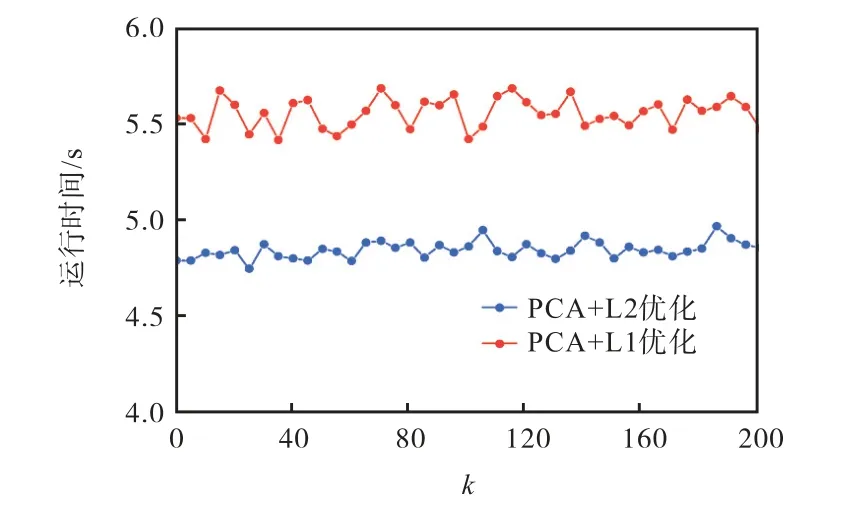
图6 固定N 的仿真时间对比Fig.6 Simulation time comparison under fixed N

为了与文献[15]和文献[16]中的传统优化算法仿真做对比，在此对4 种算法的仿真时间数据进行2 阶多项式拟合，结果如图 7 所示．可以看出，本文提出的 2 种算法运行时间较为固定，随k 值增大增幅较小．对比两种 L2 优化算法，本文的算法在 90k ＞ 时，仿真时间会低于传统 L2 优化算法，并且随着k 值的增大，仿真时间的差距更加明显；同样，在，本文的L1 优化算法的仿真时间会低于传统L1 优化算法．

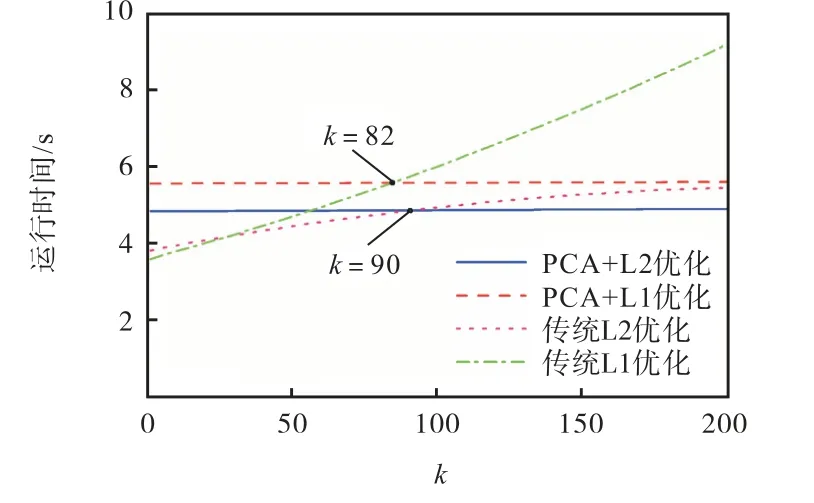
图7 不同算法的仿真时间Fig.7 Simulation time of different algorithms

因低压配电网结构较为复杂，通常含有大量节点，使得拓扑矩阵的求解变得困难，另由于智能仪表存在的损失和噪声对拓扑识别影响巨大，低压配电网的拓扑识别需要大量的数据采样点才能实现准确识别，这种情况下，本文提出的算法在运行时间上具有的良好表现．

5 结 论

本文就低压配电网拓扑结构的识别这一实际问题，提出了一种基于 PCA 和凸优化理论的低压配电网拓扑识别方法．与现有方法相比，本文方法有以下优势．

(1) 该方法利用 PCA 对数据集进行降维处理，将拓扑矩阵的计算转换为与测量时间隔离采样点无关的优化求解问题．

(2) 利用范数逼近原理和凸松弛将低压配电网拓扑识别问题转化为可解的凸优化问题，解决了其他优化算法容易陷入局部最优解的问题．

(3) 与传统优化方法相比，该方法的运行时间受采样点数的影响较小，使得该方法在大型低压配电网和数据集规模较大的场景下具有较高的应用价值.

本文提出的低压配电网拓扑识别方法有一定的实际意义，但该方法的理论体系较为简单，因此可以在基于电能守恒定律的线性模型中结合传感器的微能量收集评价技术，并提出适应于微能量收集技术应用下的低压配电网拓扑识别方法．