基于回收期的科技创新项目决策模型分析
徐龙华
(1.安康学院数学与统计学院,陕西 安康725000;2.安康学院数学与应用数学研究所,陕西 安康725000;3.陕南生态经济研究中心,陕西 安康725000)
1.引言
在对一个科技创新项目决定是否投资时,有多种方法可供决策者参考.标准的NPV方法是许多文献中经常推荐的方法,而对回收期方法颇有争议.根据回收期法,回收期较短的项目应该优先考虑.但在不确定情形下,很容易构造一个例子说明回收期较短的项目不一定能具有较大的净现值,即不一定使企业获得最大的收益,此时,回收期法与NPV法对同一项目进行决策时,可能会导致不同的决策.对资本受到限制的科技创新公司来说,利用回收期法可能较好,因为较早的收回成本可以使科技创新公司可以从事之后的项目开发.但对资金充足的科技创新公司来说,NPV法则是他们更好的选择.投资项目在企业经营发展中具有重要的作用,合理选择投资项目内容,合理配置投资方案,对于实现科技创新企业主体的可持续发展来说非常重要.
科技创新公司通常通过计算预期回报率和投资回收期来评估投资机会,许多科技创新公司要求在几年内收回投资支出,要求更高的隐含回报率.因此,许多科技创新公司的资本支出决策对利率变化并不直接敏感.尽管最低回报率和投资回收期都提供了一个客观的决策规则来作为支出决策的依据,但整个决策过程往往具有高度的主观性.目前,大部分科技创新公司都采用回收期法来评价项目,那么为什么回收期法会这么受欢迎呢?本文将会回答这个问题.
对于传统的NPV方法看起来似乎是一个很合理的评价方法,然而,在不确定下的投资时,诸多文献如文[1-6]都指出了NPV方法的不合理性和缺点.传统的方法只适用于那些不可逆转的投资行为,即管理人员根据目前已知的或预测的信息对投资项目作出决策,然后观察和控制将要发生的情况.然而这类方法却不适用于下述情况:企业有机会等待和观察那些与投资项目有关的不确定性因素,等待事态发展到一定程度,然后作出投资决策.在这种情形下,科技创新企业的投资项目显然与股票的看涨期权很类似;所以此时即使项目的NPV为正,投资者也应该等待投资.主要原因在于传统的NPV方法没有考虑到管理者的各种管理柔性,如所谓等待期权等.即在投资之前,可能等待一段时间看事情怎样发展再决定是否投资会更好.由于实际中,回收期方法被大多数科技创新企业所采纳,而现有的文献中却很少对此做出解释.Wambach在文[7]中引入了在不确定性下回收期概念.分析了对回收期与等待期权之间的关系,得出了回收期较短的项目具有较少的等待价值.但是,Wambach是对投资决策做讨论的,在得到“回收期较短的项目是具有较少的等待价值”这个主要结论时,使用的不是直接论证的方法,而是间接推断出来的.通过对不确定性投资的实物期权[8−10]方法的研究,投资者使用投资回收期作为经验法则是合理的.本文把Wambach的模型推广到科技创新项目决策问题,并给出回收期的计算公式,直接证明了回收期与等待期权的正相关性,回收期与单位资本回报的负相关性;另外也分析了同一参数对回收期及等待期权产生的不同影响.
2.不确定性下科技创新项目的回收期
本文利用Wambach的思想,对他的基本模型作出了推广.Wambach的模型是针对投资决策的,而本文将他的模型推广到科技创新项目投资问题.因为在当今科技高速发展的时代,投资者们如何准确把握时代的脉搏,寻找市场的最佳切入点,抓住机遇,改革创新使科技创新企业立于不败之地是一个相当重要很值得探讨的问题.现在虽然许多的文献都对企业的最优进入与退出时机进行了分析,但很少考虑到科技创新企业进入某项目后,了解到该行业市场行情及发展趋势,从而具有科技创新的能力,这样,科技创新企业具有一个新的期权,即研究开发与创新的期权.[11−14]而本文引进回收期法的概念,考虑对一种简单的科技创新项目作决策的情况:再进行研究之前,一次性投入固定成本,且投资不可逆.研究成功时间具有不确定性.研究成功后,投入市场无须成本,而利润流也具有不确定性.下面就是要给出计算这种项目的回收期方法.
考虑一个科技创新公司有这样的一次投资机会:投资成本为I.进行某一研究,而研究成功时间具有不确定性.这里假定成功时间服从指数分布,即它的密度函数为f(t)=λe−λt,t ≥0,λ表示研究的努力程度.研究成功后,以零成本投入市场获取利润流P(t).P(t)也是具有不确定性,假定它服从一个几何布朗运动,即dP=αPdt+σPdz,这里dz定义一个标准的维纳过程,α和σ是常数.P的期望值是时间的增函数,即E(P(t))=P0eαt,其中α表示项目漂移率.α越大,则将来期望支付越大;σ越大,则科技创新项目的利润流的不确定性就越大.特别,支付的方差Var(P(t))=P20e2αt(eσ2t −1).只要就会有任意大的t都有P(t)>0 ,因此科技创新项目永远都有价值,这里我们假定投资者是风险中性的.因此较大的σ,并不意味要求更大的回报.在后面会给出证明,更大的σ会有更大的等待期权,即使对风险中性者来说,当不确定性更大时,等待一段时间再作决定可能是更好的.那么,对这类科技创新项目如何计算它的期望的回收期,下面我们就给出计算过程.
假如现在的利润流水平为P0,回收期设为PP(P0),根据回收期法的概念,也就是到第PP(P0)年时期望能收回成本I.我们采用记号G(X)表示从投资I开始后至第X年期间所获得的利润折现值.其中折现率为γ,γ可看作无风险利率,且假设γ >α,因此
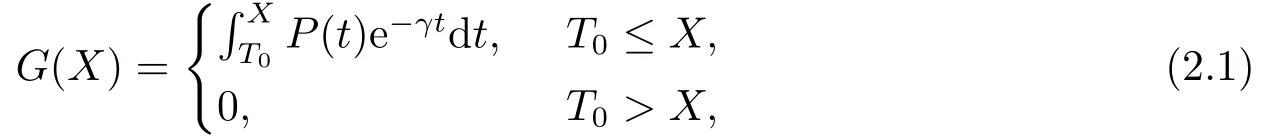
这里T0表示研究成功的时间.因为只有研究成功后科技创新公司才会获得利润流,所以当T0>X时,没有利润流,即G(X)=0.因此到第X年时科技创新公司的期望收益为:
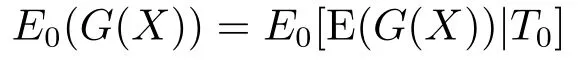
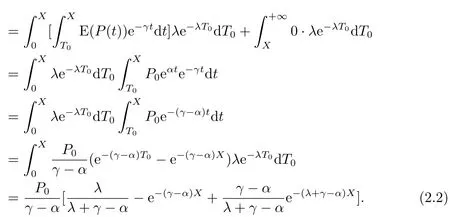
根据回收期定义,回收期内的科技创新公司期望收益等于公司对此项目的资本投资,则应有:

由(2.2)及(2.3)可知,PP(P0)满足方程:
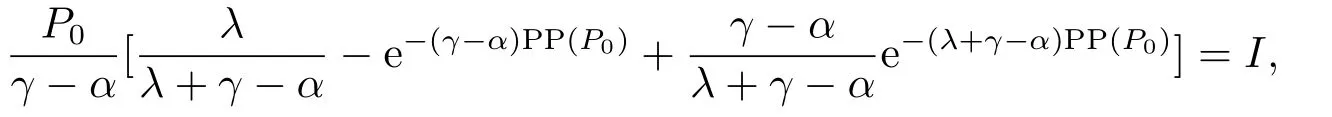
上式化简变形即得:
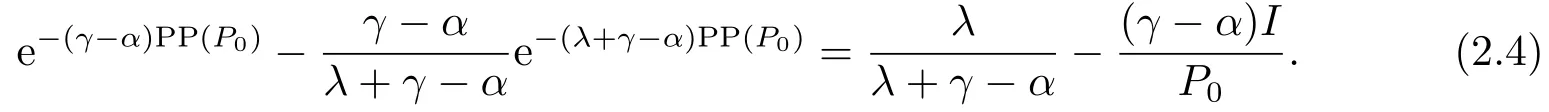
(2.4)式即为回收期PP(P0)应满足的方程.
命题1当时,方程(2.4)关于PP(P0)的解是存在唯一的.
证(2.4)式左边对PP(P0)求导,得:
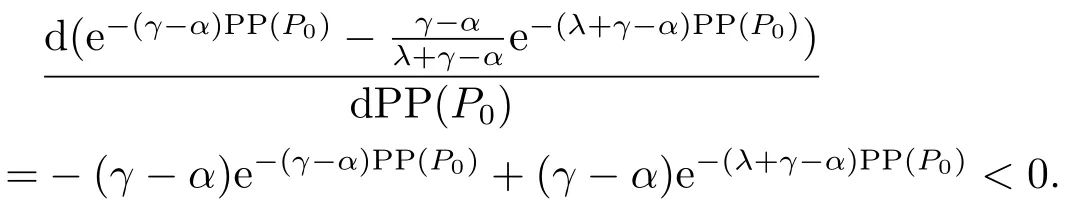
所以(2.4)式左边是关于PP(P0)的单调减函数.由于(2.4)式左边是关于PP(P0)的单调减函数,又有当PP(P0)=0时,(2.4)式左边为大于(2.4)式右边,而当PP(P0)→∞时,(2.4)式左边→0.因此(2.4)式左边的最大值为,最小值为0.由此,当时,方程(2.4)有唯一解,即存在一个有限的回收期PP(P0).
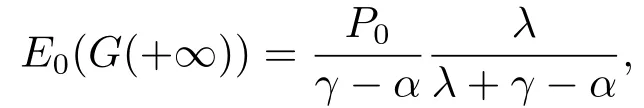
故此在利润水平为P0时投资,该项目的净现值NPV(P0)为:

以上便是对这样一种简单的科技创新项目的回收期进行计算的过程,我们得到了一个可以确定回收期的重要方程(2.4).这个方程不仅能够唯一的确定回收期,方程(2.4)的右边还可以计算总现值和净现值以及有助于得到等待期权的价值,而且这个方程可以得到各个参数对回收期的影响.
有了确定回收期的方程,就有了评价科技创新项目是否应该进行投资的指标,我们便应该考虑如何利用这个指标来做出决策,即该科技创新项目是投资还是不投资,或即刻投资或等待投资.
3.等待期权
对上面给出的这种科技创新项目,管理者是马上投资还是等待呢? 是否要根据传统的NPV法,只要现在的NPV(P0)大于零就可以进行投资? 如果现在不投资,那么什么时候才是最佳的投资时间? 或者说最优的投资决策是在P达到多大时就马上投资呢? 这个临界值P∗如何确定? 要回答这个问题,采用实物期权的思想是很有用的.投资机会可以看作是一个期权,以及实物期权的思想.我们知道了通常在做出投资决策是处在不确定的环境下的,如果光凭着科技创新项目的净现值来决定是否投资不一定是正确的,因为净现值只能决定在此刻是投资还是不投资,而不能说明在此刻投资是否能获得最大的收益.在这种情况下,我们是否要考虑等待更多的信息以获取更多价值.这就有了一个最优投资点的问题了,下面我们具体来解决这个问题.
投资者有一个支付I进行科技创新,成功后可获利润流为P(t)的期权,但他不一定立即执行这个期权,可以采取等待,在最佳时机再进行投资.为了得出这个最佳投资点,我们借用数学上,已经发展起来的在不确定性下的动态优化理论工具.考虑一个科技创新公司已经作了投资,那么它的总现值是:
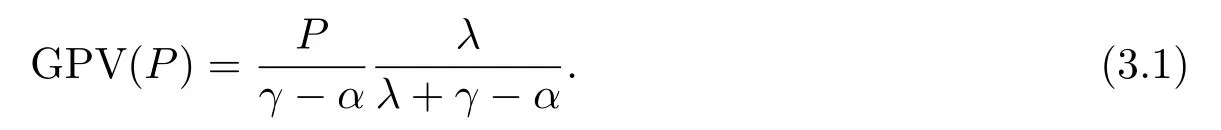
(3.1)可以由(2.5)直接得到,其中,P(t)为在t时刻已知投资的利润流.
现在,考虑一个科技创新公司还未对项目进行投资,则这个项目的价值可由贝尔曼原理得出:

这就是现在的投资期权值等于明天的投资期权值折现.只要这个投资期权没有被执行,即只要P及P+dP是小于P∗(临界值),方程(3.2)总成立.(3.2)式右边可利用伊藤引理展开:
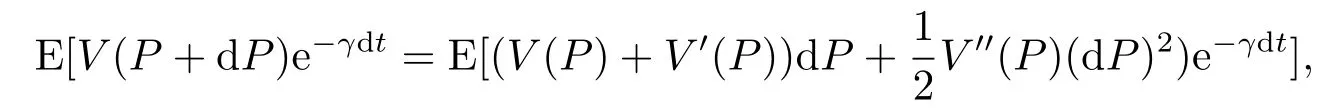
通过利用E[dP] =αPdt,E[(dP)2] =σ2P2dt,及e−γdt= 1−γdt+o(dt),代入上式得到关于V(P)的微分方程:
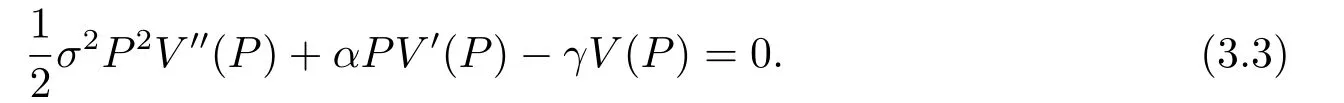
解这个方程可得到:
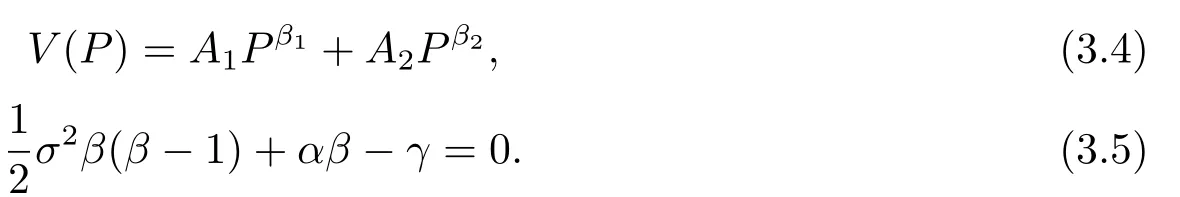
设β1,β2是方程(3.5)的两根.由于γ >α,因此由方程(3.5)可知,它的其中一根大于1,另一根小于0,我们不妨假设β1>1,β2<0.A1,A2由边界条件可确定,其中一个条件是:如果P= 0,则项目值应该为0(V(0)= 0),这一点可以直接解释,因为当P= 0 时,随机过程P(t)总会为常数值0.因此,由β2<0,可得A2= 0.至于A1的计算,则必须考虑投资的最优点时的项目价值V.我们定义这个最优点为P∗.则有两个条件必须满足:(i)值匹配条件,即投资的期权值应该等于总现值减掉投资成本;(ii)光滑通过条件,即期权值V(P)对P的偏导,在P=P∗时应等于总现值GPV对P的偏导.A1及P∗由(3.6)确定.

将式(3.1)及式(3.4)代入(3.6)可解出:
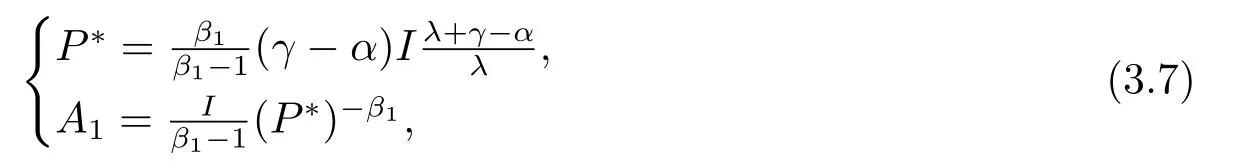
其中P∗是最优投资的临界点,这个临界点的意义在于,当P ≥P∗时,等待没有价值,则应该马上投资.如果不考虑等待柔性,传统的NPV方法对给出现值P可得出:
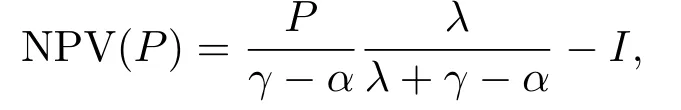
那么,当P 此时有GOW>0. 利用不确定性下的动态优化理论工具所算得的P∗是判断是否马上进行投资的关键指标.在t时刻的利润流是P,当P ≥P∗时,等待没有价值,则应该马上投资;当P 在下面第四部分我们将给出这个科技创新项目的回收期和其等待期权的价值的关系,通过回收期与等待期权的这种正相关性来解释回收期决策方法的合理性.并讨论各个参数对回收期以及等待期权的影响. 传统的财务投资理论认为,用净现值法(NPV法)来判断一项投资项目是否可行是最主要的方法.但是这种方法有很多不合理的地方,对投资项目有很多局限性.即在不确定的环境下,NPV法的有效性受到了质疑.为了考虑这些不确定性,应该要融入实物期权理论,前面提出了很多科技创新公司都是用回收期法评价项目,而已有的文献却很少解释它,这里我们通过回收期与等待期权的这种正相关性来解释它. 为了更具一般性,我们用平均单位投资成本的等待期权及平均单位投资成本的收益与回收期的长短来比较.由(3.8)式可知,因为P ≥P∗时,无需等待,立即投资,所以我们只考虑P 由(3.7)式的结果代入(4.1)式,得到: 方程(2.4)可变形为: 则(4.3)式左端表示在利润为P状态时,投资的单位回报,记为将(4.3)代入(4.2)式,可得: 然后方程两边对RUC求导,得: 由P 此可解释为,如果现在投资时的每单位回报增加,则每单位投资等待期权的价值就减少;如果现在投资时的每单位回报减少,则每单位投资等待期权的价值就增加.而另一方面,从(4.4)式有: 此可解释为,回收期越长,则每单位投资的回报越少;回收期越短,则每单位投资的回报越多.综合(4.4)与(4.5)两式可得到下面的命题2. 命题2等待投资期权与回收期正相关,即: 因此,当回收期越长时,每单位投资的回报越少,每单位投资的等待期权就会越大;而回收期越短,每单位投资的回报越多,则每单位投资的等待期权就会越少.所以,回收期越短的项目应该越早投资.这就揭示了在不确定的环境下,利用回收期法,不仅可以给科技创新公司管理者几年可收回投资的信息,还可以利用回收期与等待期权的正相关性,决定项目是应该早点投资,还是晚点投资. 下面分析参数λ,γ,α等对回收期PP(P)及等待期权GOW的影响.因为回收期PP(P)由方程(2.4)确定,(2.4)式两边对λ求导得: 变形为: 记F(PP(P))(5.1)式的右边,则,当PP(P)≥0,时, 由此可见F(PP(P))是PP(P)的增函数,当PP(P)=0时,F(0)=0,因此(5.1)式右端F(PP(P))>0,又由于(5.1)左端最后一项是负数,由此推出此可解释为当研究的努力程度增大或研究成功的期望时间下降时,则期望的回收期会减短;当研究努力程度减小,则期望的回收期会增长.这个结论是符合实际常识的. 当λ →∞时,PP(P)会达到最小,由(2.4)式可推出 (5.2)式就是文[7]的结论,因此它是本文λ →∞时的一种极端情形.由于每单位资本回报,可知当λ增大时,RUC增大.又由(4.5)式可知,在P 因为α <γ <∞,由(2.4)式即可知,当γ变大或α变小时,回收期PP(P)会变长.这里由于假定了P(t)服从几何布朗运动,而P(t)的期望值与σ无关,因此σ对回收期没有影响. 但由于(3.5)式及β1>1可知,当γ变大时,β1变大,而当α变小或γ变小时,β1会变大,因此有而由(4.2)式两边对β1求导可得: 当P γ变大或α变小,都会使GWUC变小,但是,由于γ变大或α变小,又会使单位资本回报率变小,从而由(4.4)知,会使GWUC变大.因此γ变大或α变小,可能使等待期权的变化比较模糊. 最后我们利用前面计算得到的一些公式,可以得出最优点的回收期,即在P=P∗时,投资研究开发,PP(P∗)应该满足的方程是: 即 由上述分析我们可以得到结论:在不确定性投资下,利用回收期法对科技创新项目作决策是很合理的,即使科技创新公司资金不受限制,也应该采用它作为判断的依据.因为,回收期短的科技创新项目具有较少的等待期权价值,因此应优先投资;而回收期较长的科技创新项目则应延期投资,因为等待期权价值较大.本文给出了回收期所应满足的方程,且由该方程能唯一确定回收期,以及由该方程可以得到各个参数对回收期的影响.本文是文[7]的推广模型,Wambach是对投资决策做讨论的,在得到“回收期较短的项目是具有较少的等待价值”这个主要结论时,使用的不是直接论证的方法,而是间接推断出来的.本文把他的模型推广到科技创新项目决策问题,给出回收期的计算公式,直接证明了回收期与等待期权的正相关性,回收期与单位资本回报的负相关性.另外也分析了同一参数对回收期及等待期权产生的不同影响.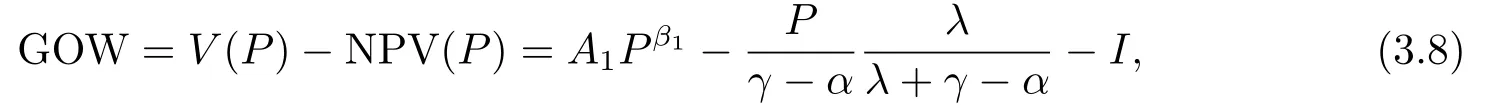
4.回收期方法的合理性
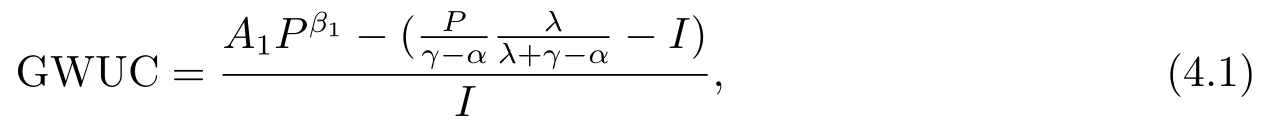
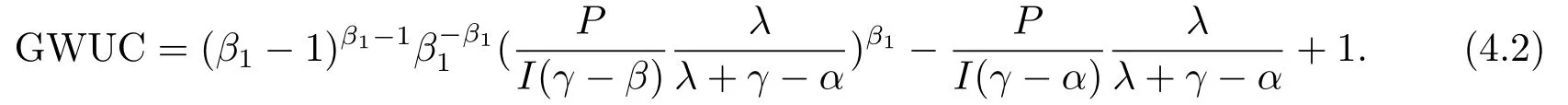
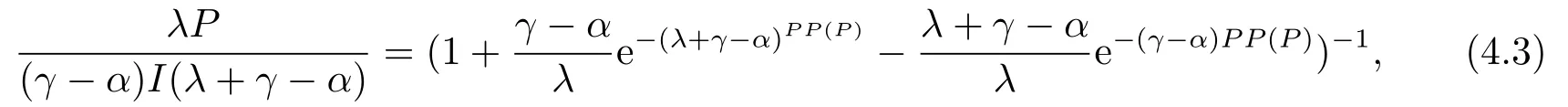
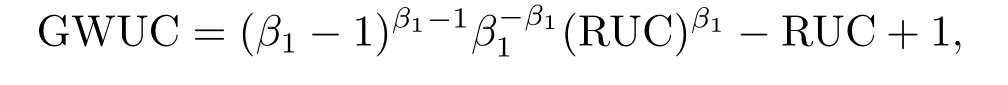
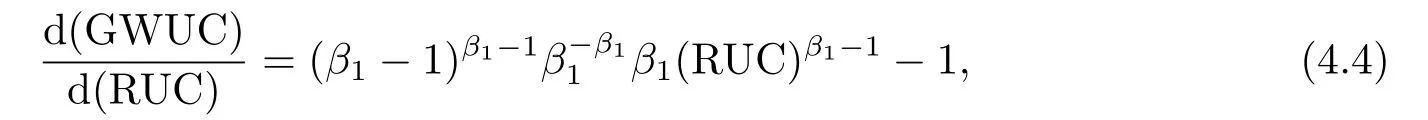
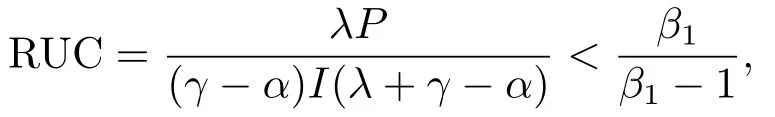
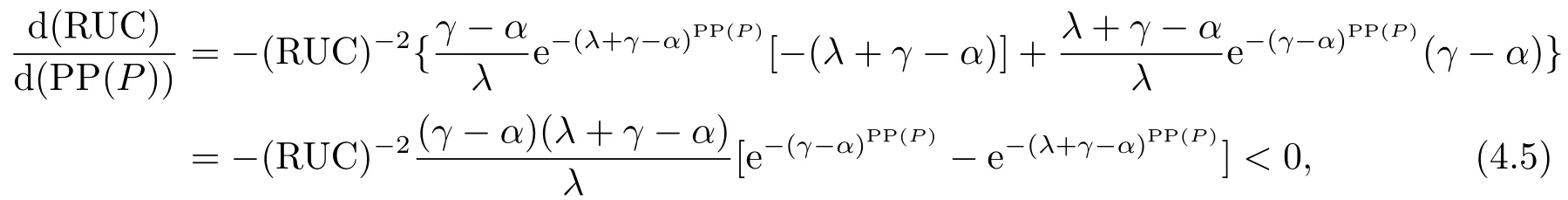
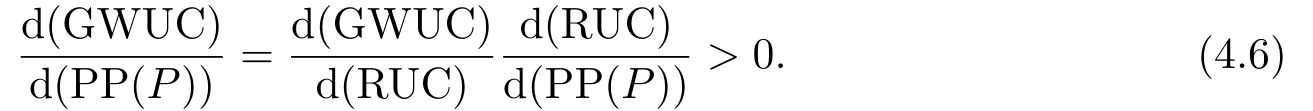
5.参数分析
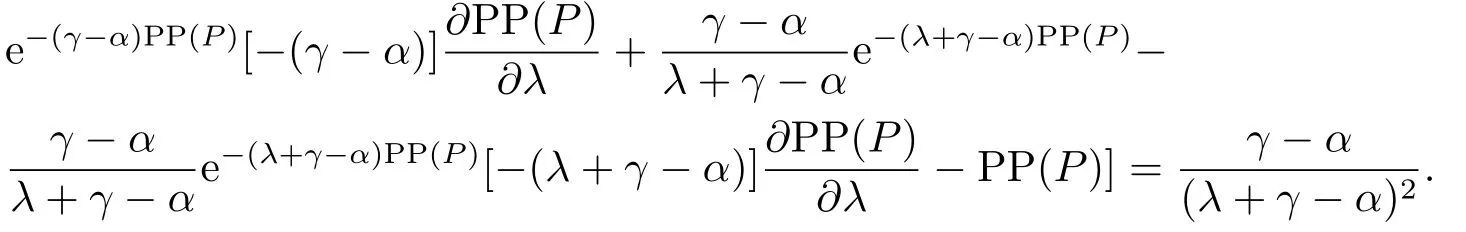
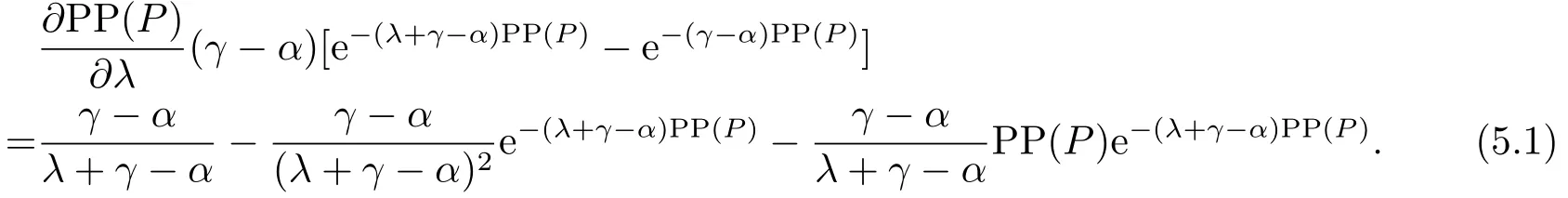
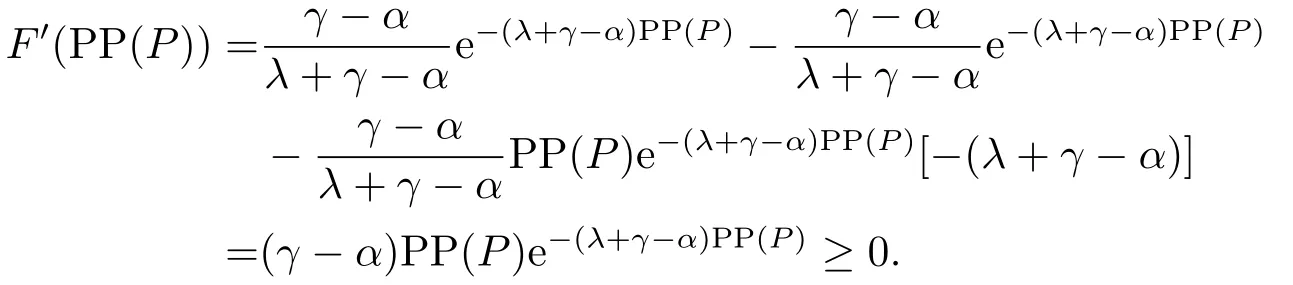
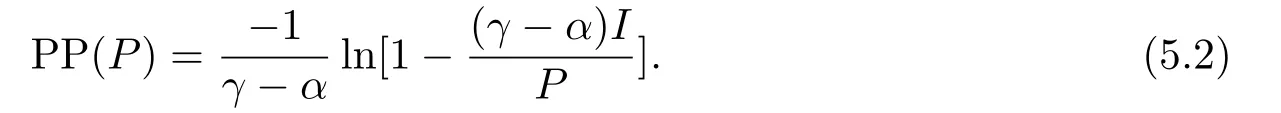
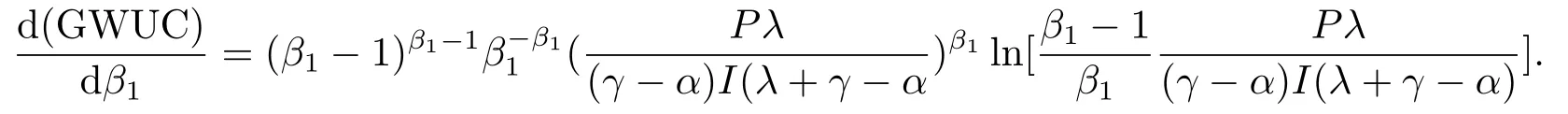
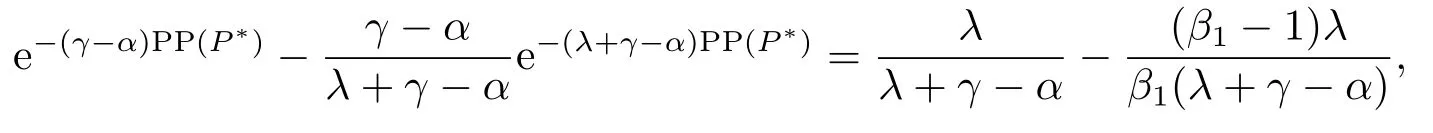
6.结论

