基于径向基逼近的KdV方程的无网格辛算法
张胜良
(南京林业大学经济管理学院,江苏 南京210037)
1.引言
本文研究一类守恒律型方程的无网格辛算法构造问题,所考虑的守恒方程具有如下形式:

这里Jx是Poisson结构(或辛结构),H是Hamilton函数,是泛函导数.例如,令Jx=∂x以及

就可以得到Korteweg-de Vries(KdV)方程:
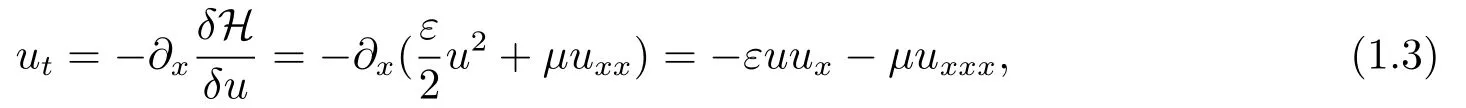
其中ε和µ都是正常数.KdV模型一直都是学术界研究的热点问题[12].一些学者研究KdV方程的显式解,比如文[8].由于显式解难以推导,因而学者提出了一些数值解法[5−6,9−10].
另一方面,系统(1.1)是一个Hamilton系统,它具有辛结构.因而数值求解Hamilton系统,也需要保持辛结构守恒.在这个指导思想下,学者提出并发展了一些经典辛算法[1−2,11].经典辛算法的构造多是结合传统的基于网格类方法,如有限差分方法、有限元方法、谱方法等,因而面临不规则区域求解问题、散乱采集点问题等挑战.
基于径向基逼近理论,本文将研究KdV方程的无网格辛算法构造问题,基于径向基无网格理论构造辛算法是新的研究视角,具有原创性.径向基方法是一种理想的无网格逼近方法,它不仅在工程技术领域得到广泛应用,而且被广泛应用于科学计算领域[3−4,7].
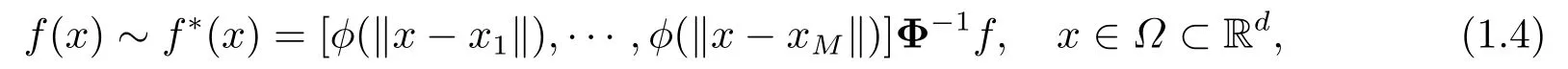
其中ϕ(r)是径向基函数,向量f= [f(x1),··· ,f(xM)]T以及插值矩阵Φ = (ϕ(∥xi −xj∥)).另外根据文[13],导数具有逼近形式:

这里γ=(γ1,··· ,γd),γj ∈Z,ℓ是对导数的逼近阶.
本文结构如下.在第二节,我们通过径向基空间离散Hamilton函数以及Poisson结构,将KdV方程转化为一个有限维的Hamilton系统.在第三节,利用辛积分子时间离散有限维系统,就可以构造出无网格的辛算法.本节进一步讨论了所构造辛算法的守恒性和收敛性.第四节给出了一些数值例子来验证理论.第五节进行简单总结.
2.KdV方程的Hamilton形式以及径向基空间离散
一个无穷维的Hamilton 系统具有三个要素:
1)一个相结构空间z ∈Z;
2)一个Hamilton函数H:R;
3)一个Poisson括号{F,G},满足反对称条件{F,G}=−{G,F}以及Jacobi等式
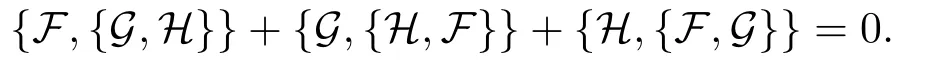
则这个系统就有Hamilton形式:
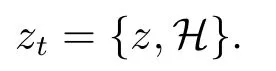
KdV方程(1.3)是无穷维的Hamilton系统的一类,它保持能量(1.2)守恒,这是因为在适合的边界条件下,
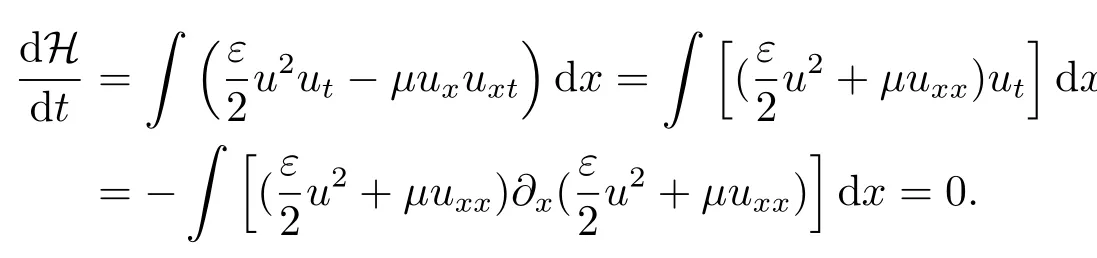
这里表示关于u的泛函导数,其定义为
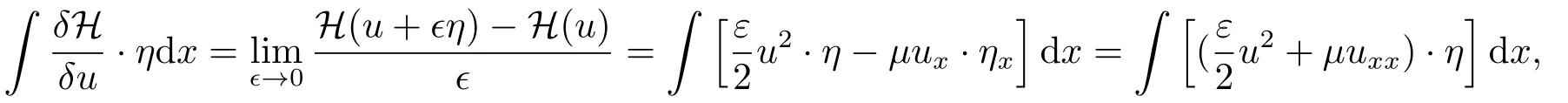
其中η是紧支柱函数,在边界点取值为0.如果选取Poisson结构
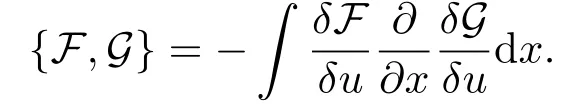
则KdV方程可以写成Hamilton系统的形式

更多关于Hamilton偏微分方程的内容可以参考文[2].
本文利用径向基插值,分别离散Hamilton函数H和Poisson括号.如果令Φ(x)= [ϕ(∥x −x1∥),··· ,ϕ(∥x −xM∥)]T,根据式(1.4),可以得到
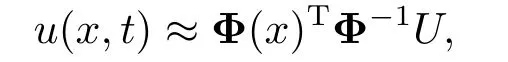
这里U=[u(x1,t),··· ,u(xM,t)]T.进一步根据径向基的导数逼近公式(1.5),有
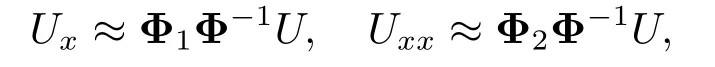
其中Ux=[ux(x1,t),...,ux(xM,t)]T,Uxx=[uxx(x1,t),...,uxx(xM,t)]T,Φ1=(ϕx(xi −xj))以及Φ2=(ϕxx(xi −xj)).因此,算子‘∂x’有逼近形式Φ1Φ−1,算子‘∂xx’有逼近形式Φ2Φ−1.
下面从两个方面来看空间离散方式:
IH(u)的径向基空间离散
讨论离散之前,我们先给出引理.
引理2.1[14]如果以及积分dw存在.令Φ(·)=ϕ(∥·∥),假设当w →0.取核函数Φc(x)=Φ(1/c)/c,则成立不等式
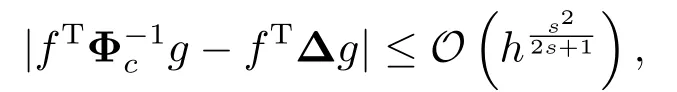
根据引理2.1,Φ−1≈∆.再由上文分析Φ2Φ−1U ≈Uxx,因此可以按下列方式离散Hamilton函数H:
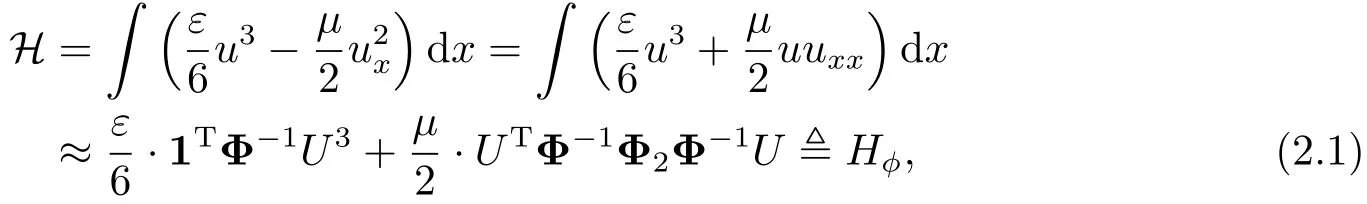
其中向量1=[1,··· ,1]T.因而
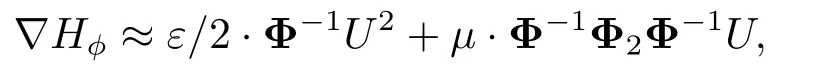
这里∇Hϕ=[...,∂uiHϕ,...]T.
II Poisson括号的径向基空间离散
相应的Poisson括号可以离散为
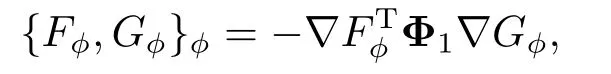
这里∇Fϕ= [...,∂uiFϕ,...]T以及∇Gϕ= [...,∂uiGϕ,...]T.因为Φ1是反对称矩阵(径向基核函数Φ(x)通常是正定的,它的导数是反对称的).容易验证{Fϕ,Gϕ}ϕ=−{Gϕ,Fϕ}以及成立Jacobi等式
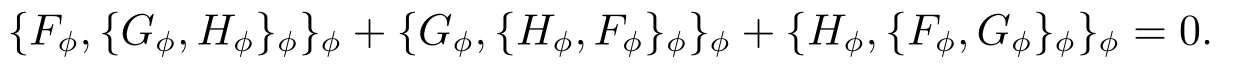
因而得到KdV方程的径向基空间离散形式
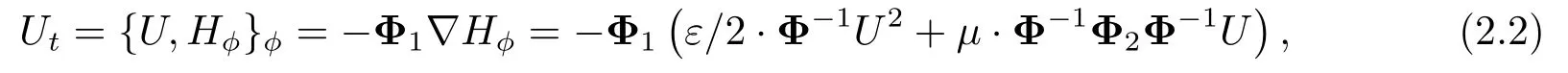
这是一个有限维的Hamilton系统.
接下来证明离散的Poisson括号{Fϕ,Gϕ}ϕ是连续{F,G}的一个逼近.
定理2.1令h=maxx∈Ωminj ∥x −xj∥表示数据点的密度,当h →0,则有
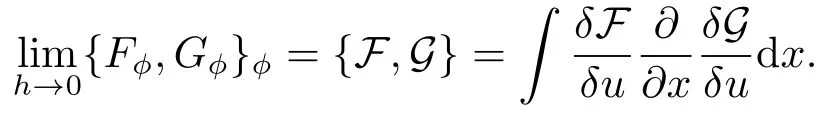
证首先,根据泛函导数的定义以及数值积分公式
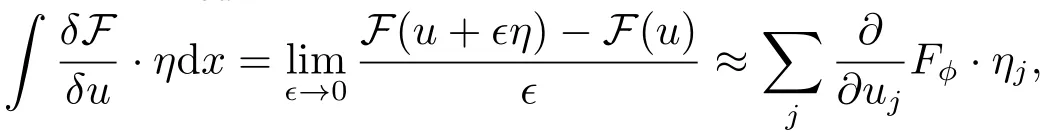
可以得到
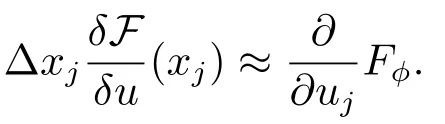
注意到∂x ≈Φ1Φ−1,Φ−1≈∆(引理2.1),因此,当h →0时,离散Poisson括号
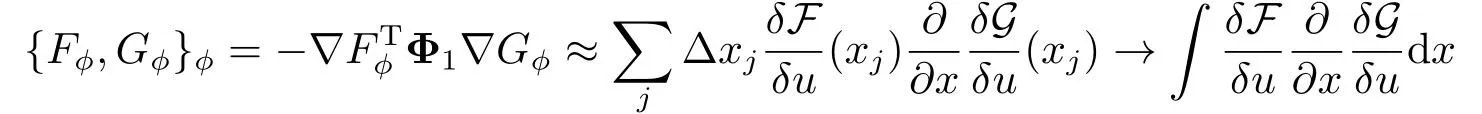
成立.
3.辛积分子空间离散以及辛算法
在时间方向上,利用Euler中点格式离散方程(2.2),就可以得到KdV方程的无网格辛算法:
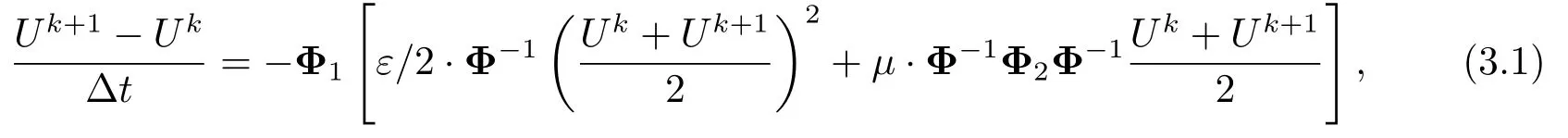
这里,Uk={u(xj,tk)},tk=t0+k∆t.定义截断误差
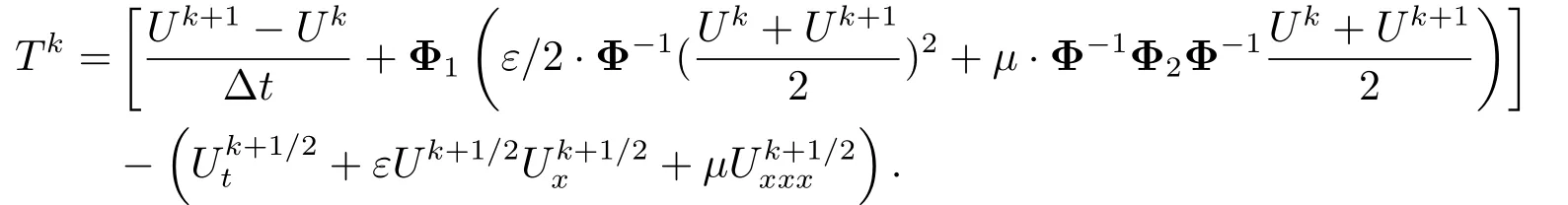
令∥·∥表示L2范数,则有如下定理.
定理3.1假设u(x,t)∈H10(R)∩H2(R),∀t ∈[0,T],u(x,t)∈C4(R),∀x.则Tk有估计式
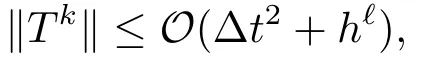
这里ℓ是径向基逼近两阶导数的误差阶.
证根据Taylor展开,下式成立
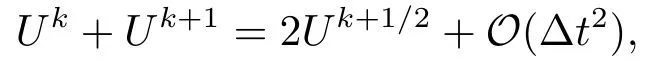
以及
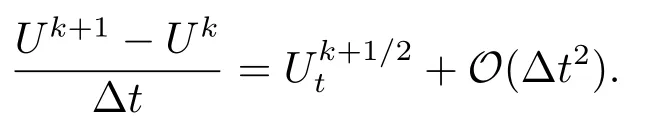
因此,有
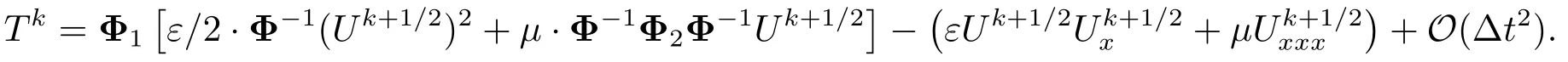
注意到Φ1Φ−1和Φ2Φ−1是∂x和∂xx的逼近,逼近阶是ℓ.因此
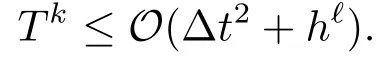
4.数值例子
本节给出两个例子来说明所构造无网格辛算法的精度和效率.例4.1给出一个单孤立波,用来验证,无论配置点是等距还是非等距的,所构造辛算法都是高精度的.例4.1也验证所构造辛算法具有长时间跟踪能力.例4.2用来说明,当求解两列波交叉的例子,算法效果依然很好.
例4.1考虑具有单孤立波的KdV方程(1.3)这里ε=6,µ=1.初始条件
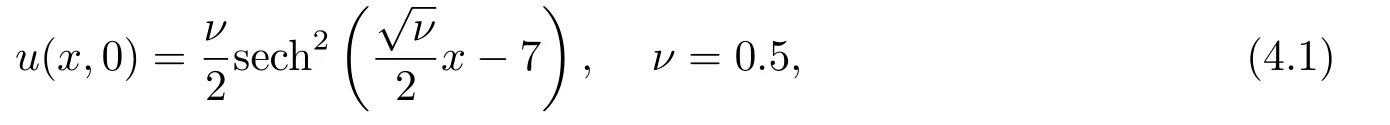
此时解析解为

定义均方误差L2以及最大误差L∞分别为
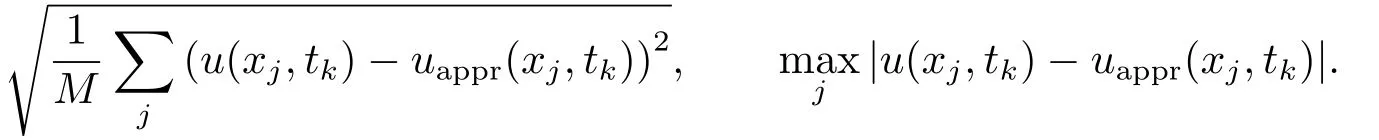
选择Gaussian 径向基函数(GSϕ(x)=exp(−r2/2c2)),取形状参数c=0.6.首先在区间[0,40]内取M个均匀分布点,以及t=1做精度测试,数值计算结果列在表4.1.表4.1说明,所构造的辛算法具有较高的逼近度(逼近阶为4.27).
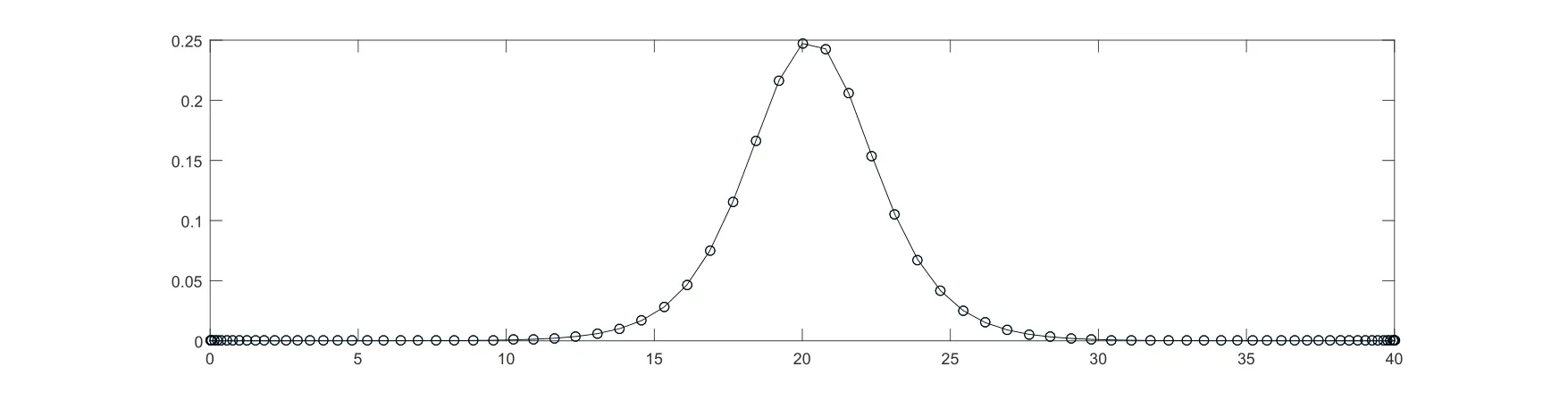
图4.1 t=1时真实解(实线)和数值解(圆圈)比较(非等据点,单孤立波)
图4.2验证了所构造辛算法具有长期跟踪能力,当我们计算到t= 30,在30000步(∆t=0.001)之后,数值依然精确的模拟出真实解.所需时间不超过5秒,说明该方法是高效率的.
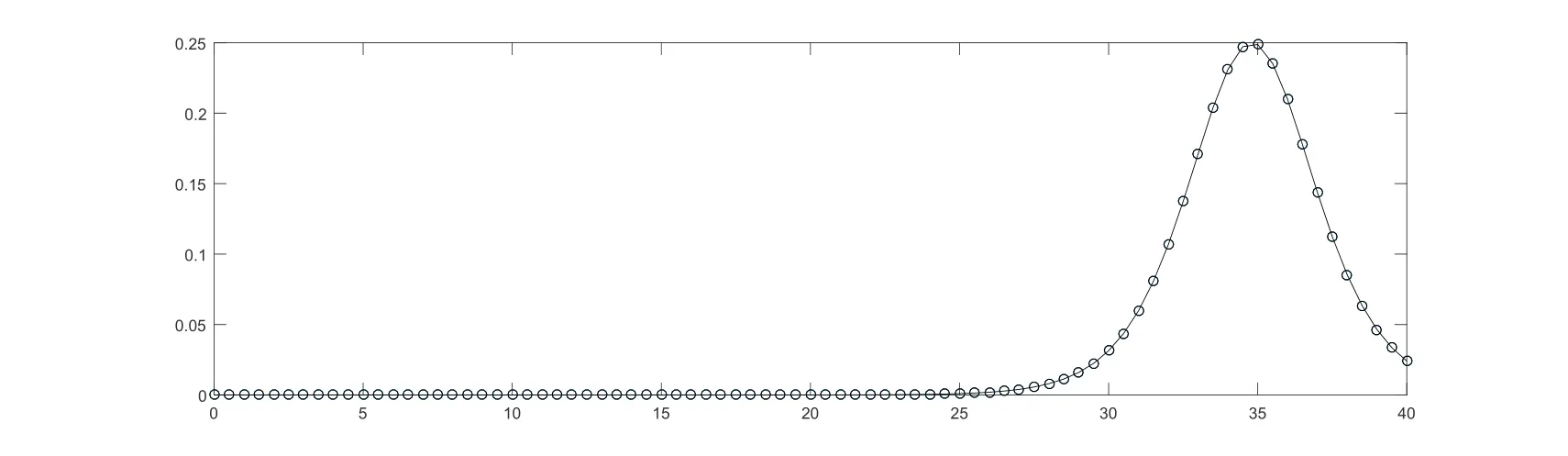
图4.2 t=30时真实解(实线)和数值解(圆圈)比较(等据点,单孤立波)
例4.2考虑交叉孤立波方程(1.3),仍取ε=6以及µ=1.给定精确解为
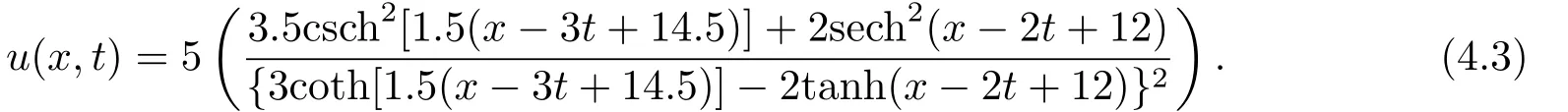
所需初边值条件可以从精确解中提取.在数值程序中,选择逆multiquadric径向基函数(IMQs形状参数c= 1.2,以及在区间[−20,60]选择400个等据点做模拟.数值模拟结果如图4.3.

图4.3 数值解(圆圈)和真实解(实线)比较(等据点,两列波交叉)
5.结论
基于径向基逼近理论,本文为KdV方程构造了一个高精度的无网格辛算法.理论分析了该算法的收敛性,并给出了误差界估计.数值例子验证了理论结果,表明所构造的辛算法是高精度的、无网格的、具有长期跟踪能力.

