面向分布式电源接入配电网的电力优化模型研究
唐 伟,周 杨,李大全,谢巨龙
(1.珠海横琴能源发展有限公司,广东 珠海 519031) (2.广州健新科技股份有限公司,广东 广州 510530)
近年来,化石能源的枯竭和生态环境的恶化对人类社会的可持续发展构成了严重的威胁[1]。在能源危机和环境保护的双重压力下,清洁和可再生能源的快速发展成为能源战略的重点,越来越多的分布式能源(distribute generation,DG)、配电终端和新型电力设备连接到配电网[2]。这些新型的电力设备虽缓解了电力短缺,却也导致配电网拓扑变得越来越复杂、三相不平衡问题越来越突出[3]。因此,研究用于分布式电源接入配电网的电力优化模型具有重要的现实意义。
当前,许多学者从各种角度研究DG的位置和容量优化问题:文献[4]建立的多目标优化配置模型,以电压、电流质量和网络损耗为优化目标;文献[5],针对DG的接入位置和容量配置建立的多目标优化模型,以最小网损、最大静态电压稳定、最小投资成本为优化目标;文献[6],针对网络损耗、电压质量和电流质量这3个指标建立了DG接入的多目标优化模型;文献[7]建立的DG接入优化配置模型,以投资收益最大化为优化目标;文献[8]建立的DG接入多目标优化配置模型,以网络损耗、线路热稳定性和静态电压稳定为优化目标。可见,目前对DG接入配电网的优化配置模型的研究有许多不同的目标函数,多目标智能优化配置方法还需要加强。
在上述研究的基础上,本文通过建立多目标优化模型,以有功网损和静态电压稳定性为优化目标,将Logistic混沌遍历技术与粒子群优化算法有效结合,对模型进行求解。
1 优化模型
配电网规划的目标是满足用户的供电需求、确保电网正常运行[9]。本文使用有功损耗和静态电压稳定性这两个指标来建立双目标优化模型,该模型体现的是配置经济性和安全性。
1.1 目标函数
1)网络的有功损耗。
DG合理地接入配电网会减少分支潮流和有功损耗,配置不当和注入量过多会增加支路潮流并增加损耗[10]。网络的有功损耗优化指标如式(1)所示。
(1)
式中:fploss为系统有功损耗;N为网络节点总数;i为支路k的首节点;Pi和Qi分别为首节点i的有功功率和无功功率;Ui为首节点i的电压幅度;rk为支路k的电阻。
2)静态电压稳定性。
由于大量DG接入配电网络会对配电网的电压稳定性产生较大影响,因此需要对电压稳定性进行研究。配电网电压稳定性指标如式(2)所示[11]:
Ustab,k=4[(XPj-RQj)2+(XQj+
(2)
式中:Ustab,k为第k个支路的电压稳定性指标(首节点i和末节点j);R和X分别为支路k的电阻和电抗;Pj和Qj分别为末节点j流入的有功功率和无功功率。
当系统稳定时,每个支路的电压稳定度指标小于1.0;当系统故障时,从系统的弱分支开始,电压的稳定性由Ustab,k与临界值1.0的距离来判断[12]。
各支路的最大电压稳定指数为整个系统的电压稳定指标fUstab,如式(3)所示:
fUstab=max{Ustab,1,Ustab,2,…,Ustab,N}
(3)
式中:Ustab,1,Ustab,2,Ustab,N分别为支路1,2和N的电压稳定指标。
3)由于文中采用的两个优化目标为不同的量纲,因此两者之间可能存在不一致之处。 为了调整各种优化目标以获得双目标优化,使用加权因子方法将两个优化目标转换为一个优化目标,数学模型转换如式(4)所示:
(4)
式中:f为双目标优化函数;plossinit和Ustabinit分别为初始网络有功损耗和静态电压稳定指数(无DG接入);a和b为网络有功损耗和静态电压稳定指标的惩罚因子;w1和w2为网络有功损耗和静态电压稳定指标的权重因子。
为了确保该网络是一个吸收辐射的网络,节点电压幅值的上限应小于变电站出口的额定电压1.0 pu,下限不得低于0.9 pu。DG接入量小于总网络负载时,网络处于吸收拓扑状态。
1.2 约束条件
目标函数约束可用节点电压、潮流、有功功率等表示。
1)节点电压Vi约束如式(5)所示[13]:
(5)

2)潮流约束如式(6)和(7)所示:
(6)
(7)
式中:PLi和QLi分别为负荷节点i的有功功率和无功功率;PDGi和QDGi分别为DG向节点i注入的有功功率和无功功率;Vi和Vj分别为节点i和节点j的电压;Gij,Bij,θij分别为节点i和j间的电导、导纳和相差角。
3)式(8)所示为节点接入的有功功率约束[14]:
PDGmin (8) 式中:PDGmin和PDGmax分别为DG注入的有功功率下限和上限。 算法具有适应性强、算法简单、精度高等优势[15],但是首领粒子的主动搜索能力很弱,不利于粒子的局部深度搜索和全局搜索,并且对求解精度有很大影响。为了解决这个问题,本文引入Logistic混沌遍历技术,以此提高粒子群优化算法的主动性。 将Logistic混沌遍历技术和粒子群优化算法相结合,利用Logistic技术在搜索区域内生成遍历位置,就能提高粒子群算法的整体搜索能力;而赋予粒子群算法主动探测概率,则能提高粒子群算法的局部深度搜索能力。 1)提高全局搜索能力。 将Logistic混沌遍历技术和粒子群优化算法相结合,为粒子探测和搜索提供参考点x(t,d)。粒子主动搜索随机动态邻域U(x(t,d),δ(d)),搜索后更新首领粒子全局最优gbest,从而提高粒子群算法的全局优化能力。参考点序列x(t,d)的定义如式(9)、(10)和(11)所示: x(t,d)=a(d)×cx(t+200,d) (9) cx(t,d)=a(d)×cx(t-1,d)×[1-cx(t-1,d)] (10) a(d)=4.1+0.1×rand (11) 式中:t为当前迭代时间;d为当前搜索区域的维度;cx(t,d)为Logistic混沌序列;a(d)为资源系数;rand为在区间[0,1]上的随机数。 t时刻随机动态邻域如式(12)所示: (12) 2)提高局部深度搜索能力。 改进的PSO算法步骤如下: 步骤1:初始化。初始化种群大小M、粒子位置x、速度v、学习因子c1和c2、惯性加权系数ω、迭代次数k、粒子个体最优解pbestid和全局最优解gbest等。选择混沌的初始值cx(t,d)=rand。 步骤2:计算每个粒子的适应度值,更新粒子个体最优解pbestid和全局最优解gbest。计算粒子群主动搜索概率P(t),如果P(t) 步骤3:对粒子速度v和位置x进行更新。 步骤4:如果满足终止条件或达到迭代次数,执行下一步。否则,迭代次数加1,返回到步骤2。 步骤5:输出结果。 图1所示为基于Logistic混沌遍历技术优化的PSO算法优化过程。 图1 改进PSO算法流程 采用PG&E69典型配电系统用于仿真测试。系统的参考电压为12.66 kV,基准功率为100 MV·A。在优化结果中,电压稳定指标用于表示系统的静态电压稳定指数。图2中所示配电网系统用于仿真各种类型的区域最优配置问题。 图2 PG&E69配电系统 在网络中设置4个DG优化区域(图2中带有虚线的框):区域矩阵Ⅰ,NDG为50~54;区域矩阵Ⅱ,NDG为20~27;区域矩阵Ⅲ,NDG为32~35,37~39;区域矩阵Ⅳ,NDG为66~69。种群数为50,最大迭代次数为100,惯性权重系数为0.6,学习因子为1.5和1.0。不接DG时,有功损耗为226.473 5 kW。电压稳定性指标为0.125 7,节点最低电压为0.918 3 pu。文中以双馈异步风力机为PQ节点,异步风力机是PQ(V)节点,太阳能是PI节点,燃料电池和燃气轮机是PV节点。 为了验证改进PSO算法处理分布式电源优化配置的能力,将优化结果与粒子群优化和量子粒子群优化进行了比较。在配电网中优化配置一个DG为PQ节点。功率因数为1(即只产生有功功率)时,以有功损耗最小为优化目标,优化结果见表1。 表1 69节点配置结果 本文算法的参数与其他两种算法的参数相同。由表1可知,本文算法的配置容量虽然比粒子群优化和量子粒子群优化算法稍高,但其有效损耗降低率最高,显示了该算法的优越性。结果表明,本文算法能够正确地优化分布式电源配置,并最大程度地降低了网络的有功损耗。 在指定区域内,一个区域配置一个DG,DG被分为两种方案进行仿真分析。 方案1:分别针对区域Ⅰ、区域Ⅱ和区域Ⅲ优化PI、PQ(V)和PQ节点类型配置。每个节点的最大容量为1 200 kW,下限为150 kW。 方案2:分别针对区域Ⅰ、区域Ⅲ和区域Ⅳ优化PI,PQ(V)和PQ节点类型配置。区域Ⅰ、Ⅲ的节点容量的上限和下限分别为1 200 kW和150 kW。区域Ⅳ节点的容量上限和下限分别为1 200 kW和0。图3所示为两种方案接入DG之前和之后系统节点的电压幅值曲线。优化结果见表2。 由图3和表2可知,在方案1中,与初始网络相比,网络的有功损耗和电压稳定性指数分别降低了77.40%和62.00%,节点的最低电压从0.918 3 pu上升到0.960 0 pu。在方案2中,与初始网络相比,网络的有功损耗和电压稳定性指数分别降低了73.14%和61.65%,节点的最低电压从0.918 3 pu上升到0.959 2 pu。 图3 两种方案接入DG前后的电压幅值对比 表2 优化配置结果 在位置固定的情况下,需要优化接入容量,分析网络有功损耗和电压稳定性受DG接入位置和容量的影响,接入节点分别指定为20和50,各节点接入容量上下限分别为2 400 kW和150 kW。 表3给出了在固定DG位置进行容量优化(方案3)的结果。 表3 节点配置结果 方案3分别在20节点和50节点优化配置了一个PV节点DG,在20节点和50节点分别接入200 kW和990 kW容量的PV节点DG。优化后的网络有功损耗和电压稳定性指标分别比初始网络降低77.07%和82.90%。 从图4可以看出,优化配置后,20节点的电压幅值从初始的0.959 2 pu增加到0.980 1 pu,50节点的电压幅度从0.912 1 pu增加到0.980 0 pu,增幅较大,表明文中提出的优化配置方法可以较好地解决PV节点型DG的优化问题,可减少网络损耗并提高电压稳定性。 图4 方案3接入DG前后的电压幅值 为了测试双目标优化的优势,本文基于单网络有功损耗、静态电压稳定性指标和双目标优化函数对DG网络容量进行了优化。仿真实验选择69节点系统。DG的位置固定为20和50节点,PQ节点类型DG用于仿真计算,功率因数为0.9。DG容量的上下限设置为2 400 kW和150 kW。3种目标函数的优化结果见表4。 表4 目标函数优化结果比较 由表4可知:1)最小化网络有功损耗的单目标优化可以实现较低的损耗,但电压稳定指数相对较高,安全性有待提高;2)单目标电压稳定优化可以提高系统安全性,但会增加网络损耗;3)与单一目标相比,使用双目标时优化结果不是最优的,而是兼顾了两个函数的优势。 本文验证了建立的多目标优化模型的有效性和准确性,结论如下: 1)改进的粒子群优化算法在分布式电源的优化配置中优于单一优化算法,并能最大限度地降低网络有功损耗。 2)与单目标优化相比,双目标函数优化不是最优的,但兼顾了两者的优点。 考虑到当前实验设备和数据的规模,本文的研究还处于起步阶段。基于此,对优化模型进行持续的完善和改进是下一步工作的重点。2 改进PSO算法

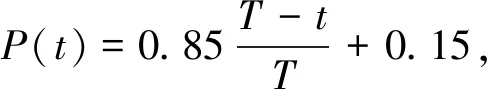

3 仿真分析
3.1 仿真参数

3.2 算法优化对比

3.3 DG数量限制的区域优化配置
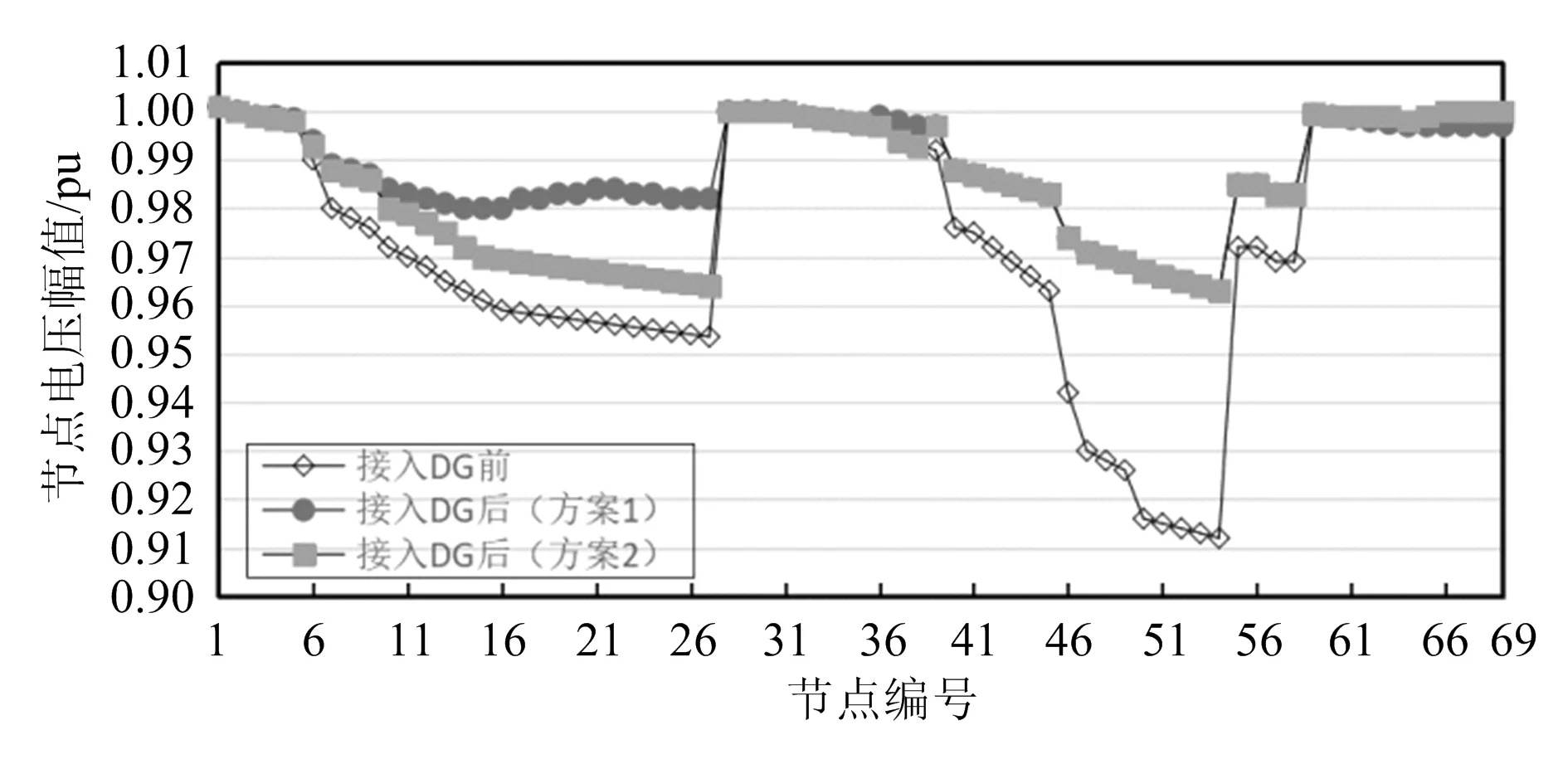

3.4 DG位置固定的区域优化配置


3.5 双目标函数配置的优越性

4 结论

