基于Workbench的风机塔门强度分析及优化

徐东杰，陈进建，童跃平，黄文才，邹渊士，赵佰余，朱斌辉

(华仪风能有限公司，浙江 温州 325000)

塔架是风电机组的重要组成部分，起到支撑整机、为风轮提供足够高度、为机组安全运行提供保障的作用[1]。近年来，随着风机容量及塔架高度的增加，风机载荷越来越大，如何设计出一款兼顾可靠性与经济性的塔架已成为各整机厂亟需解决的重要课题。塔门一般设于塔架近地面附近，便于运维人员及设备进出。作为塔架设计的重要环节，合理的塔门结构除需要有良好的工艺性和经济性，更要能够缓解因局部形状突变引发的应力集中，使塔架满足规范中有关强度及屈曲等方面的要求。

随着风电行业的发展，国内外许多学者对塔门结构设计展开了研究。Dimopoulos等[2]使用有限元法对4种不同加强方案的门洞结构进行了分析，得出门洞的承载能力并没有随着塔门形式的复杂化而明显加强的结论；孟令锐等[3]探讨了门框厚度及其内外定位尺寸对塔门应力的影响，并使用遗传算法对门框进行了多目标优化；汪亚洲等[4]采用ANSYS软件建立了门框的有限元模型，对其进行了强度分析，并完成了危险应力点处的尺寸优化；晏红文等[5]基于Isight平台，集成Pro/E和ABAQUS软件，利用ASA模拟退火全局优化算法对塔架门框进行优化设计，优化中考虑了部分门框的外形尺寸对优化结果的影响；任瑞杰等[6]计算了四组塔壁/门框厚度尺寸组合下塔门的应力，分析了各变量对门框极限应力及其出现位置的影响，但忽略了塔门定位尺寸的影响。

本文借助Workbench平台，基于GL2010风机设计规范[7]分析了某MW级风力发电机塔门强度，全面考虑影响塔门应力的各个几何参数，采用Workbench的DesignXplorer模块以塔门质量及等效应力最小为目标进行结构优化，优化后塔门安全性及经济性有了较大改善。

1 初始设计分析

1.1 有限元模型

基于Workbench对塔架门框初始设计进行有限元分析，采用图1所示GL塔底坐标系进行建模，保守考虑将门框位置设在塔架迎风面正前方。

图1 GL2010塔架坐标系

某MW级风力发电机组塔架门框为椭圆形门框，初始设计尺寸如图2所示，塔架梯子、平台、电缆等内附件以及混凝土地基对塔门强度的影响忽略不计。

采用Solid186高阶单元进行网格划分，并细化门框及其附近区域网格,划分后的单元数量为399 918，节点数为750 099。

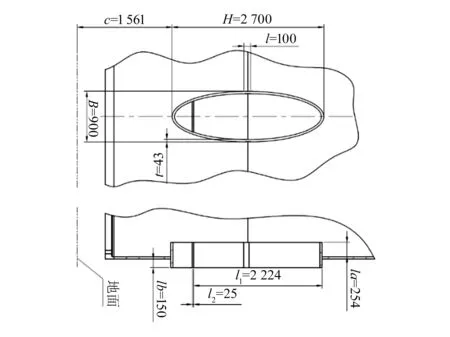
图2 门框初始设计尺寸

1.2 材料性能

塔架主体采用Q355ND高强度结构钢，法兰及门框采用Q355NE高强度结构钢，Q355ND和Q355NE的弹性模量均为2.1×105MPa，泊松比为0.3，密度为7.85×10-9t/mm3。由 GB/T 1591—2018《低合金高强度结构钢》[8]可知其材料属性，具体见表1。

表1 Q355ND与Q355NE上屈服强度最小值

1.3 载荷与边界条件

对塔架底法兰处节点的自由度进行固定约束，加载点与该段塔架顶部进行绑定连接，形成载荷伞，用于传递载荷。施加边界条件后的塔架模型如图3所示。

图3 施加完边界条件的塔架模型

通过风机动力学软件Bladed提取塔底载荷，包括弯矩Mx和My、扭矩Mz、推力Fx和Fy、压力Fz，在塔底加载最恶劣的弯矩极限工况载荷见表2。

表2 加载点施加的极限载荷

1.4 结果分析

根据上述加载和边界条件计算得到应力云图如图4所示，由图可知，门横板处最大等效应力为231.07 MPa，门框焊缝处最大等效应力为286.0 MPa。

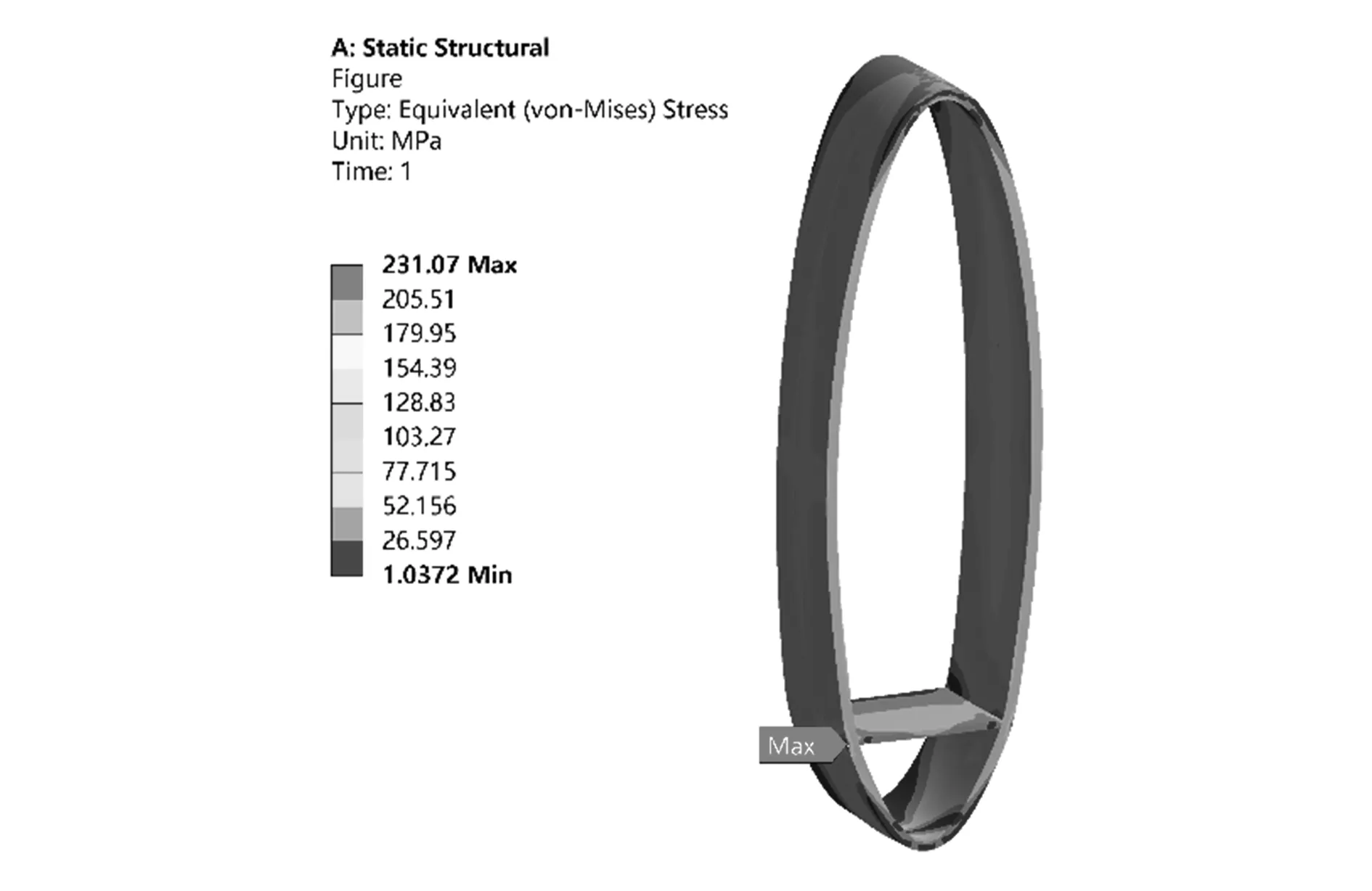
图4 塔架门横板处极限工况应力云图

根据IIW规范[9]，焊缝位置的应力需通过外推处理获得，即通过焊缝两侧距离焊趾0.4倍钢板厚度和1.0倍钢板厚度位置的节点应力外推得到门框焊缝处应力σhs，外推公式如下：

σhs=1.67σ0.4·t-0.67σ1.0·t

(1)

式中：σ0.4·t为距焊趾0.4倍钢板厚度处的应力分量，t为钢板厚度；σ1.0·t为距焊趾1.0倍钢板厚度处的应力分量。

完成外推工作后得到门框焊缝处的各个应力分量，将其合成等效应力σe。等效应力的计算公式如下：

(2)

式中：σz,σy,σz为正应力分量；τxy,τyz,τzx为切应力分量。

外推后门框焊缝处最大等效应力为167.4 MPa。钢板厚度为43 mm和46 mm时，材料的屈服强度规定值不小于335 MPa。门框极限强度安全余量SME计算公式如下：

(3)

式中：ReH为材料屈服强度；γm为材料安全系数，取值1.1；σeqvmax为等效应力的最大值。

经计算，横板处强度安全余量为30.8%，门框焊缝处强度安全余量为81.9%，满足设计要求，且余量较大，可对塔门结构进行优化。

2 优化模型建立

2.1 设计变量

通过分析得到影响塔门应力的几何设计变量，其取值范围见表3，各变量位置如图2所示。

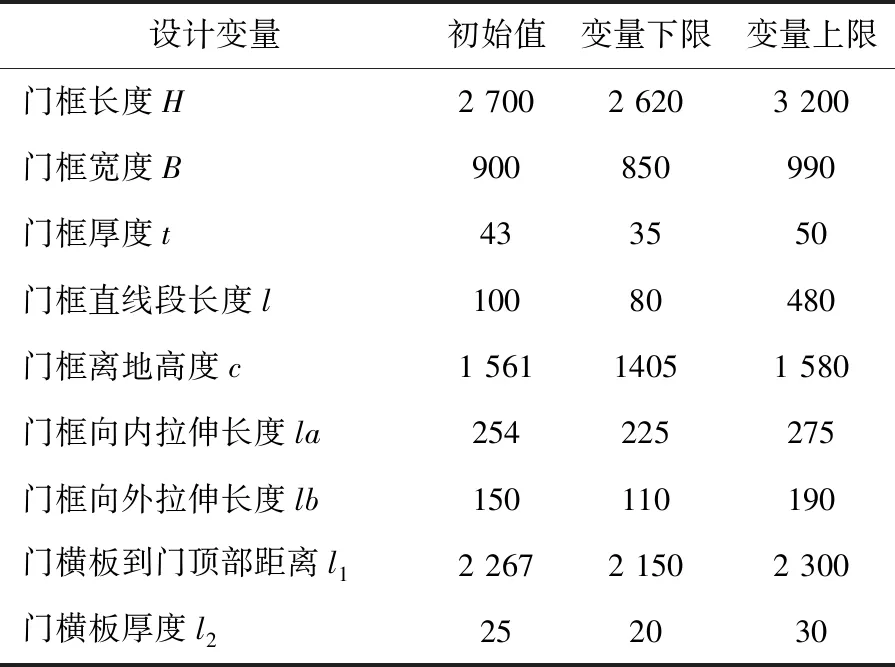
表3 设计变量及取值范围 单位：mm

2.2 约束条件

1)强度约束条件：门横板和焊缝处的最大等效应力不超过Q355NE钢材许用应力304.5 MPa。

2)优化变量约束条件：见表3。

2.3 目标函数

Rn=(H,B,c,l,c,la,lb,l1,l2)

(4)

式中：R为有效解集；D为向量目标函数；x为有效解；F(x)为等效应力函数响应值；G(x)为质量函数响应值。

3 响应面模型

响应面近似模型的构建是通过一系列样本点来确定近似函数中的待定参数，通过选取样本点和迭代策略，来保证近似响应函数能够逼近真实的隐式响应函数，可以与有限元分析结合起来对复杂结构响应进行研究。

3.1 实验设计

实验设计[10](DOE)中样本点的选取直接影响计算成本和响应面精度。本文采用最优空间填充设计法(OSF)，该方法随机生成样本点，设计空间更均匀，适合于复杂响应面。

3.2 响应面质量

基于OSF实验设计结果，使用Kriging响应面[11]，该类型响应面能处理变化较剧烈的情况，常用验证点来评价精度。如图5所示，纵轴为响应面预测值，横轴为设计点计算值。验证点和响应面较为接近，散点基本位于45°线，故认为响应面质量较好。

图5 预测值与计算值散点图

3.3 敏感性分析

门横板处最大等效应力与各设计变量的相关性如图6所示，由图可知，对门横板处最大等效应力影响最大的是负相关的门框厚度t，次之是正相关的门框长度H。

图6 门横板处最大等效应力敏感性分析结果

门框焊缝处最大等效应力与各设计变量的相关性如图7所示，由图可知，对门框焊缝处最大等效应力影响最大的是负相关的门框长度H，次之是正相关的门框向外拉伸长度lb。

图7 门框焊缝处最大等效应力敏感性分析结果

门框质量与各设计变量的相关性如图8所示，由图可知，对门框质量影响最大的是正相关的门框厚度t，次之是正相关的门框向外拉伸长度lb。

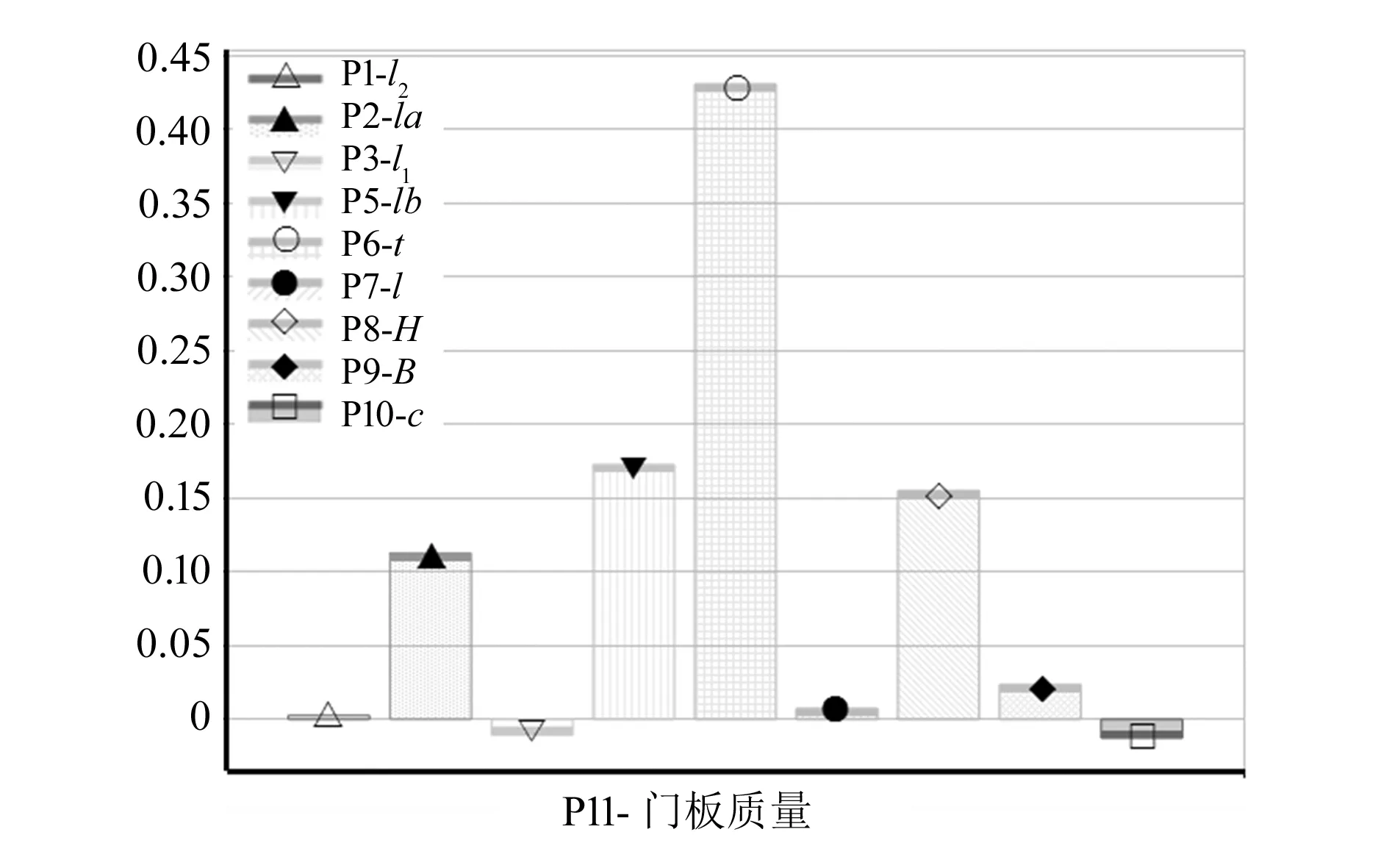
图8 门框质量敏感性分析结果

3.4 响应图分析

基于敏感性分析结果，选取对门横板处最大等效应力和门框焊缝处最大等效应力影响最大的两个设计变量，使用响应图进行分析。

图9 t和H对门横板处最大等效应力影响

由图9可以看出，当门框长度H在2 780.3～3 000.0 mm范围内变动时，对门横板最大等效应力产生主要影响的是t，且呈现负相关。

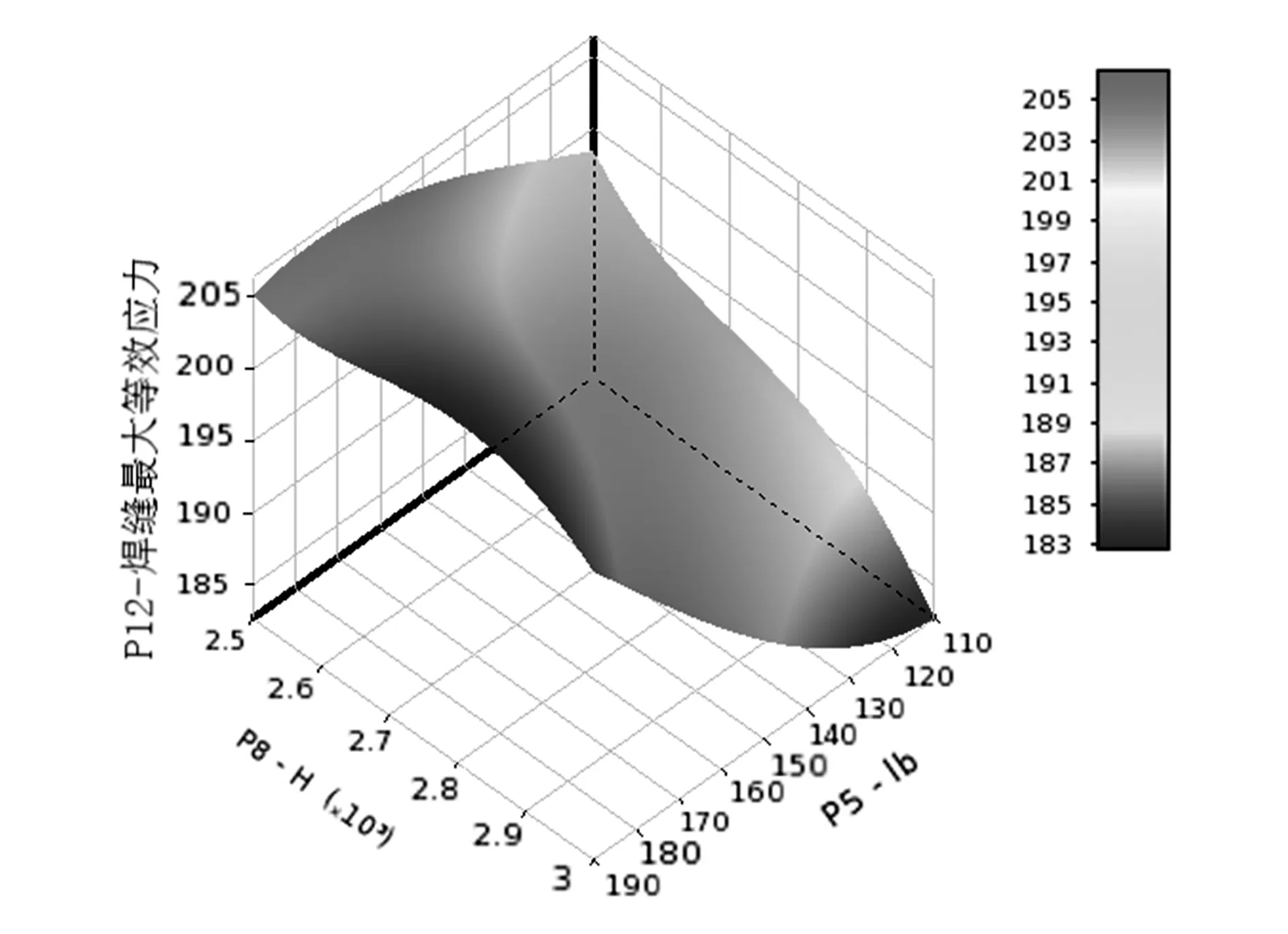
图10 H和lb对门框焊缝处最大等效应力影响

由图10可以看出，当门框长度H在2 500.0～2 600.0 mm范围内变动时，对门框焊缝处最大等效应力产生主要影响的是门框长度H，且呈现负相关。

上述结论与敏感性分析的结论一致，进一步验证了响应面的准确性。

4 目标优化

首先使用Screening法找到近似优化解，然后在此基础上使用基于遗传算法的多目标优化方法进行全局最优设计。多目标优化算法是基于Pareto最优化理论的Tradeoff研究求出一系列含备选设计的集合，即帕累托前沿(Pareto Front)，帕累托前沿中的解不受前沿外的解所支配，拥有最少的目标冲突，可提供一个较佳的选择空间。

经过优化计算，得到部分最优候选点，见表4，由表可知，候选点4的门框质量最轻，且门横板和门框焊缝处的应力满足设计要求。经过制造工艺评估，为避免焊缝热影响区过近，门框直线段长度需大于100 mm，故选择候选点6为最优候选点。

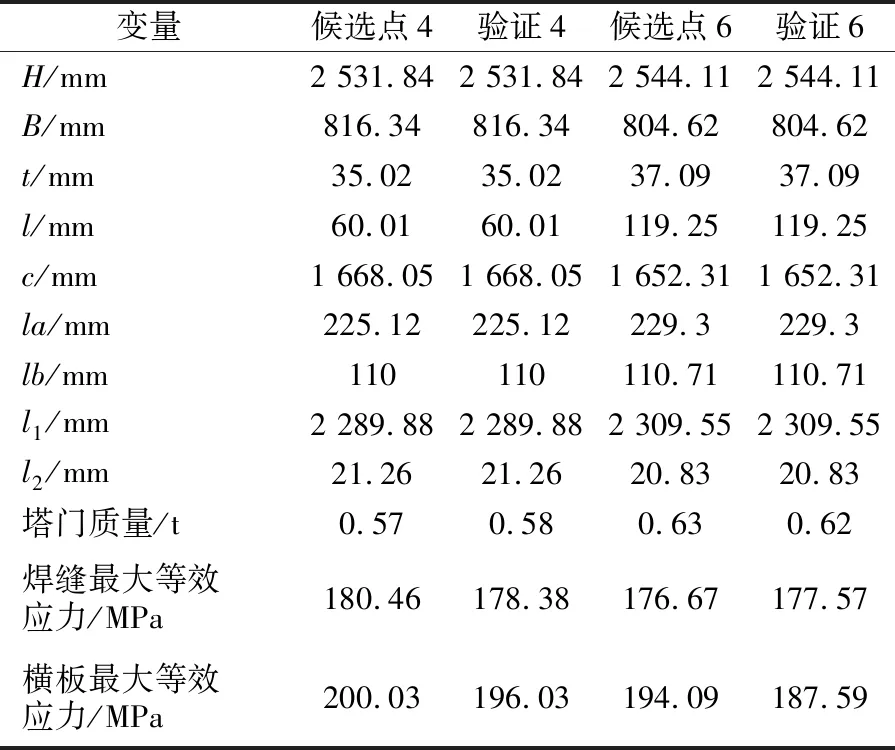
表4 最优候选点

将候选点6的数据进行圆整，使用该设计变量配置下的门框圆整后的数据进行强度计算，结果见表5。优化后门框质量减少了34.8%，门横板的最大等效应力降低了8.0%，门框焊缝外推的最大等效应力降低了9.4%，门框强度安全余量提高了11.4%。优化后的门框达到了降本的经济性要求，并满足使用要求。

5 结论

本文使用有限元法对风机塔架塔门进行了强度分析及优化设计，得到主要结论如下：

1)对门横板处等效应力最大值影响最大的是负相关的门框厚度t；对门框焊缝处等效应力最大值影响最大的是负相关的门框长度H；对门框质量影响最大的是正相关的门框厚度t。

表5 优化前后结果对比

2)优化后的门框质量减少了34.8%，门横板处的最大等效应力降低了8.0%，门框焊缝外推的最大等效应力降低了9.4%，优化效果显著。

本文阐述的塔门分析及优化方法易用、可靠，相关结论对塔门结构设计有一定指导意义。