3-RRR并联机构SolidWorks和MATLAB运动学仿真分析

罗建国，王 婷，聂高兴，王宇强

(1.华北科技学院机电工程学院，河北 三河 065201) (2.河北省矿山设备安全监测重点实验室，河北 三河 065201) (3.华北科技学院安全工程学院，河北 三河 065201) (4.太原理工大学机械与运载工程学院，山西 太原 030024)

并联机构具有刚度大、结构稳定、动态性能好等优点[1]，其中平面三自由度并联机构广泛应用于机械精密加工、军事、医学等领域[2-3]，逐渐成为机构学研究领域的热点。许多学者对平面三自由度并联机构进行了研究，并提出了多种不同类型的平面三自由度并联机构，其中3-RRR就是一种灵活度较高、操作性强的平面三自由度并联机构[4]。冯志坚等[5]采用数值法对三自由度并联机构进行位置求解，并结合ADAMS软件仿真分析，得到该机构的动力学速度、加速度曲线。刘伟等[6]采用代数消元法对3-RPS并联机构进行运动学位置求解。刘震[7]基于方位特征集和数值法分析3-UPU并联机构的运动特性、位置求解、工作空间，得到了该机构的运动空间轨迹。宋轶民等[8]通过分析对比3-RRR和4-RRR并联机构的运动学模型，发现3-RRR并联机构的耦合度低，即冗余支链增加了机构耦合度，对奇异位形造成了影响。黄剑锋等[9]基于ADAMS软件建立3-RRR并联机构模型，得到了该机构的位移及速度曲线。许多学者基于数值法和代数消元法对运动学位置进行求解，但求解过程比较复杂。随着科学技术的发展，并联机构被广泛应用于各行各业，因此通过分析并联机构的耦合度，进而采取更加安全、有效、合理的措施，就可以减轻奇异位形造成的损失。本文以3-RRR并联机构为研究对象分析该机构的耦合度，对于并联机构的解耦具有非常重要的意义。

1 机构耦合度分析

本文构建的3-RRR并联机构运动简图如图1所示。该机构由定平台A、动平台C和3条相同的支链RRR构成。设θi为AiBi绕转动副Ai的轴线逆时针旋转至与o-x轴平行的转角；φi为CiBi与通过点Bi的轴线的夹角，旋转方向为逆时针；ai为转动副Ai和转动副Bi轴线之间的距离，a1=a2=a3=a；bi为转动副Bi和转动副Ci轴线之间的距离，b1=b2=b3=b；r为动平台内接圆半径；R为静平台内接圆半径。其中θi,φi的大小由机构的位形决定，ai,bi,r,R由机构本身的结构确定，其中i=1,2,3。

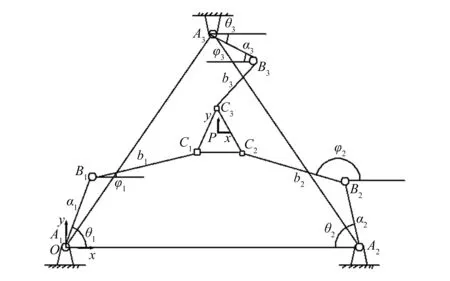
图1 平面3-RRR并联机构

本文基于有序单开链(SOC)进行机构耦合度和运动学位置求解，步骤如下：首先，由于任一机构都是由若干个基本运动链(BKC)组成，因此可将3-RRR拓扑机构基本运动链分解成约束度为正、负、零3种不同的序单开链，并计算其各自的约束度，其中序单开链按照自由度不可再分的是基本运动链。其次，在按机构的基本运动链计算出约束度后，再通过其约束度(Δj)计算耦合度(κ):当SOC约束度的数值为正时，SOC支链自由度增加，由此可增加κ个虚拟变量，进而建立包含虚拟变量的位置方程；当SOC约束度的数值为零时，SOC支链自由度不发生变化，不需设立虚拟变量，即可单独求解位置方程；当SOC约束度的数值为负时，SOC支链自由度减少，位置方程求解比较困难,因此可通过设立虚拟变量建立约束方程。最后，利用数学方法求解位置方程。该方法可将位置求解过程简化成求解各个有序单开链的位置，过程简单，思路清晰。

基于上述理论基础，将该机构的拓扑结构分为2条支链，分别为SOC1{-A1-B1-C1-C2-B2-A2}、SOC2{-A3-B3-C3-}，计算其各自的约束度，其数学表达式如式(1)所示：

(1)

式中：Δj为第j个单开链的约束度；mj为第j个单开链的运动副数目；fi为第i个运动副的自由度；Ij为第j个单开链的驱动副数目；ζLj为第j个回路的位移方程数。

将约束度Δ1，Δ2的计算结果代入耦合度κ的公式中，其数学表达式如下：

(2)

式中：ν为并联机构的基本回路数。

耦合度的数值越大，表明该机构位置求解越复杂；反之，耦合度的数值越小，表明该机构位置求解越简单。

2 位置分析

2.1 位置正解分析

3-RRR平面并联机构位置正解可简述为：已知定平台上各个主动副Ai的输入角度θi(如图1所示)、动平台坐标系上P点的坐标以及位姿角γ(如图2所示)。设动平台上点P在固定坐标系的位置为(xP,yP)，转动副Bi在定坐标系o-xy中表示如下：

(3)

式中：R为定平台内接圆半径。

图2 动平台位姿图

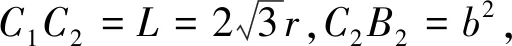
(4)

式中：x和y分别为C2的横、纵坐标；xC1和yC1分别为点C1的横、纵坐标；xB1和yB1分别为点B1的横、纵坐标。

(5)

式中：xC3和yC3分别为点C3的横、纵坐标。

在约束度Δ2<0的支链中，利用三角形几何关系建立约束方程，如式(6)所示：

f(φ1)*=(xC3-xB3)2+(yC3-yB3)2-b2=0

(6)

式中：f(φ1)*为包含虚拟变量的约束方程；xB3和yB3分别为点B3的横、纵坐标。

则动平台的位姿如式(7)所示：

(7)

式中：xC2和yC2分别为点C2的横、纵坐标。

2.2 位置逆解分析

位置逆解可简述为：已知动平台坐标系上各个转动副的坐标，求定平台上各个主动副的输入角度θi。给定P点的坐标(xP,yP)，若并联机构的动平台存在位置逆解，Bi必须存在，利用支链的几何关系可知Bi是以Ai为圆心、ai为半径的圆与以Ci为圆心、bi为半径的圆的交点，可建立如下表达式：

(8)

将各个支链各点的坐标代入式(8)，可知该方程是关于θi的方程。

(9)

综上可知，对于本文中的3-RRR并联机构，当给定位姿时，1条支链最多可有2组解，3条支链最多可有8组解，即8种位形。

3 奇异分析

奇异是所有机构都会发生的一种不可回避的现象，对于任何机构，在它的运动过程中总会或多或少地遇到特殊位置，在这些位置机构会出现特殊的现象，或者处于死点不能继续运动，或者失去稳定，甚至自由度也发生改变。当机构处于极限点、死点时，这些现象就被称为机构的奇异性。本文主要将奇异位形分为3类，如下所述：

第一类奇异位形是一条支链的主动杆和从动杆平行时，导致机构自由度发生变化，进而影响该机构的运动精度，如图3和图4所示。

第二类奇异位形分为2种情况：一种是2条支链的从动杆互相平行时，导致机构自由度发生变化；另一种是3条支链的从动杆互相平行时，产生奇异。如图5和图6所示。

图3 单支链完全伸展奇异位形 图4 单支链完全折叠奇异位形

图5 2个从动杆互相平行奇异位形 图6 3个从动杆互相平行奇异位形

第三类奇异位形为上述两种奇异类型同时出现。由于此时机构的耦合性比较强，且杆件之间的摩擦比较大，故同时出现这两种奇异位形对机构本身的损害比较大，因此在机构的设计过程中必须避免这3类奇异位形的出现。

4 仿真分析

仿真时设定3-RRR平面并联机构各个杆件尺寸为：a=300 mm,b=100 mm,R=500 mm,r=75 mm。假定该机构用于机械加工行业生产线上的物品搬运。建立如图1所示的坐标系，则动平台P点的运动轨迹可假设成以(275,330)为圆心、以75 mm为半径的圆；动平台上的转动副C2绕C1旋转，即位姿转角为20°，那么动平台中心点P的轨迹运动方程如式(10)所示：

(10)

式中：t为运动时间。

基于MATLAB软件对3-RRR并联机构进行运动学仿真，通过运算可以得到该机构的角速度、角加速度等运动曲线，如图7和图8所示，该曲线可以精确表达该机构的运动特征。

图7 角速度曲线图

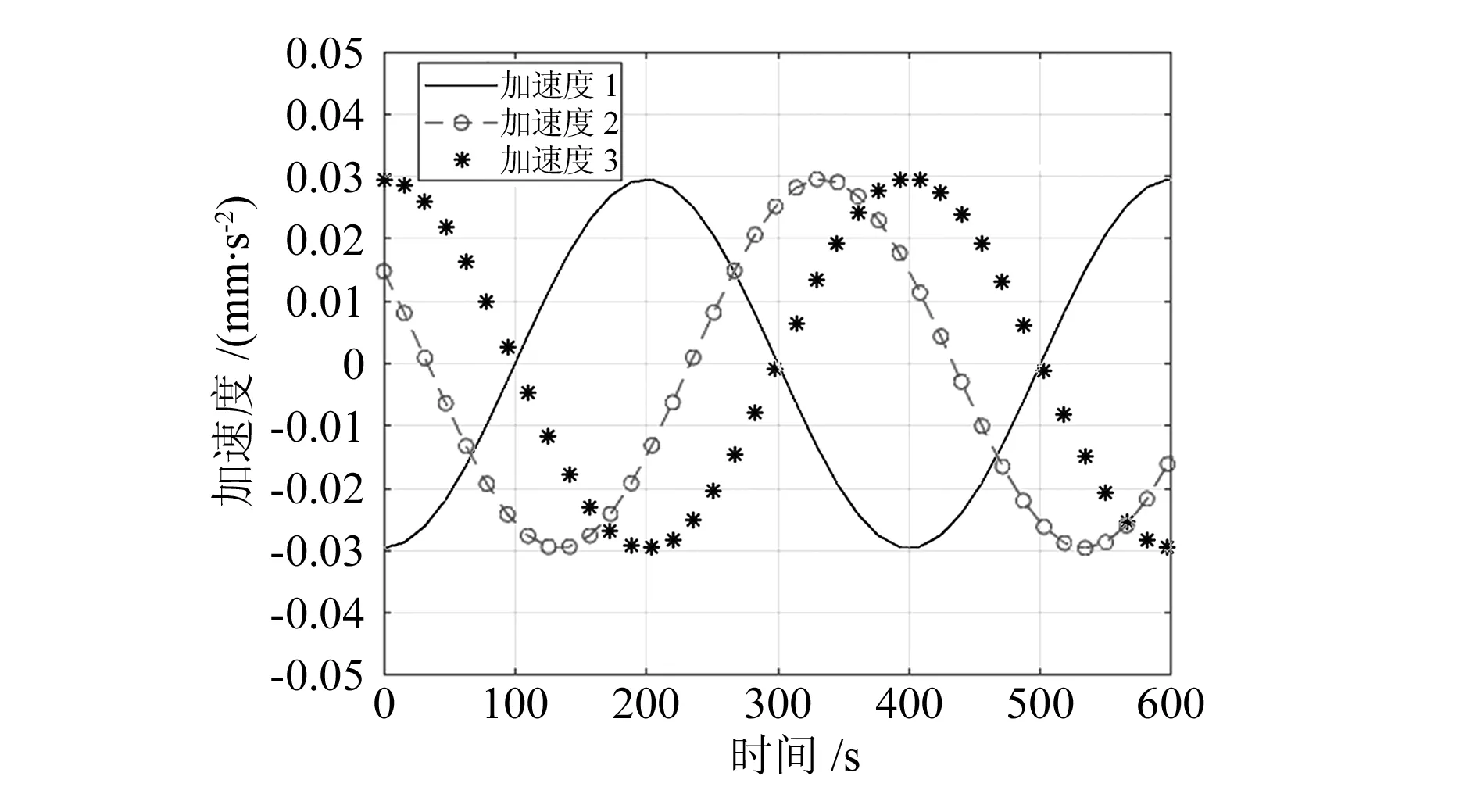
图8 角加速度曲线图

5 结束语

本文以3-RRR并联机构为研究对象，利用有序单开链法获得该机构的耦合度κ=1，即该机构属于低耦合度的并联机构，具有一定的研究价值。该方法适用于判断任意一个并联机构的耦合度，具有普遍性。但是，目前的研究工作仅通过3-RRR平面并联机构证明本文理论的实用性，该机构结构比较简单，要真正在实践中体现其价值，还需要通过编制软件将本文的理论分析过程程序化，形成一套对并联机构约束度、耦合度分析的完整理论，从而减少大量的重复工作。