湿蒸汽激励下围带碰撞-摩擦阻尼计算方法
聂凡茹,唐委校
(1.山东大学机械工程学院,山东 济南 250061) (2.高效洁净机械制造教育部重点实验室(山东大学),山东 济南 250061) (3.机械工程国家级实验教学示范中心(山东大学),山东 济南 250061)
具有复杂结构特点(长轴系、大柔性叶片和Z形围带等)的大型汽轮机转子系统在转速和湿蒸汽激励下会被诱发强非线性振动,直接影响整个汽轮机组的运行安全。目前工程上广泛采用围带来抑制转子系统振动响应和消耗振动能量。很多学者对装备围带的转子系统进行了动力学特性研究:蒋爱华[1]建立了基于Hertz接触理论的弹簧阻尼围带碰撞模型,数值分析了初始间隙和转速对转子系统主共振响应的影响规律;能海强[2]考虑摩擦系数、接触刚度、初始间隙、接触角及转速的影响,建立了弹簧碰撞-Sgn摩擦的平行四边形围带碰撞-摩擦模型,数值分析了升降速工况下接触角和初始间隙对转子系统响应特性的影响规律;何冰冰等[3]基于离心刚化效应建立了非线性弹簧-指数衰减Sgn平行四边形围带碰撞-摩擦模型,数值分析了非线性刚度比和初始间隙对振动位移响应的影响规律。刘锦[4]基于迟滞摩擦模型提出转速激励下平行四边形围带摩擦阻尼的计算方法,定量分析了接触角、初始间隙、摩擦系数和接触刚度对围带摩擦阻尼和系统振动特性的影响规律。郭冰[5]基于迟滞摩擦模型提出转速和湿蒸汽多频激励下平行四边形围带摩擦阻尼的计算方法,数值分析了不同流量下进气参数和不同转速对系统振动响应的影响规律。
针对现有Z形围带阻尼模型未能考虑围带间相对滑动速度影响,计算方法无法定量计算出考虑围带间相对滑动速度影响的Z形围带碰撞-摩擦阻尼等问题,本文以大型汽轮机Z形围带为例,建立在转速和湿蒸汽激励下考虑围带间相对滑动速度影响的Z形围带弹簧碰撞-指数衰减迟滞摩擦模型,提出一种围带碰撞-摩擦阻尼计算方法,定量计算围带阻尼对转子系统振动特性的影响。
1 Z形围带碰撞-摩擦阻尼模型及其计算公式
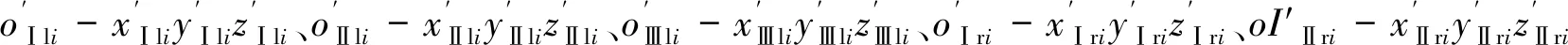
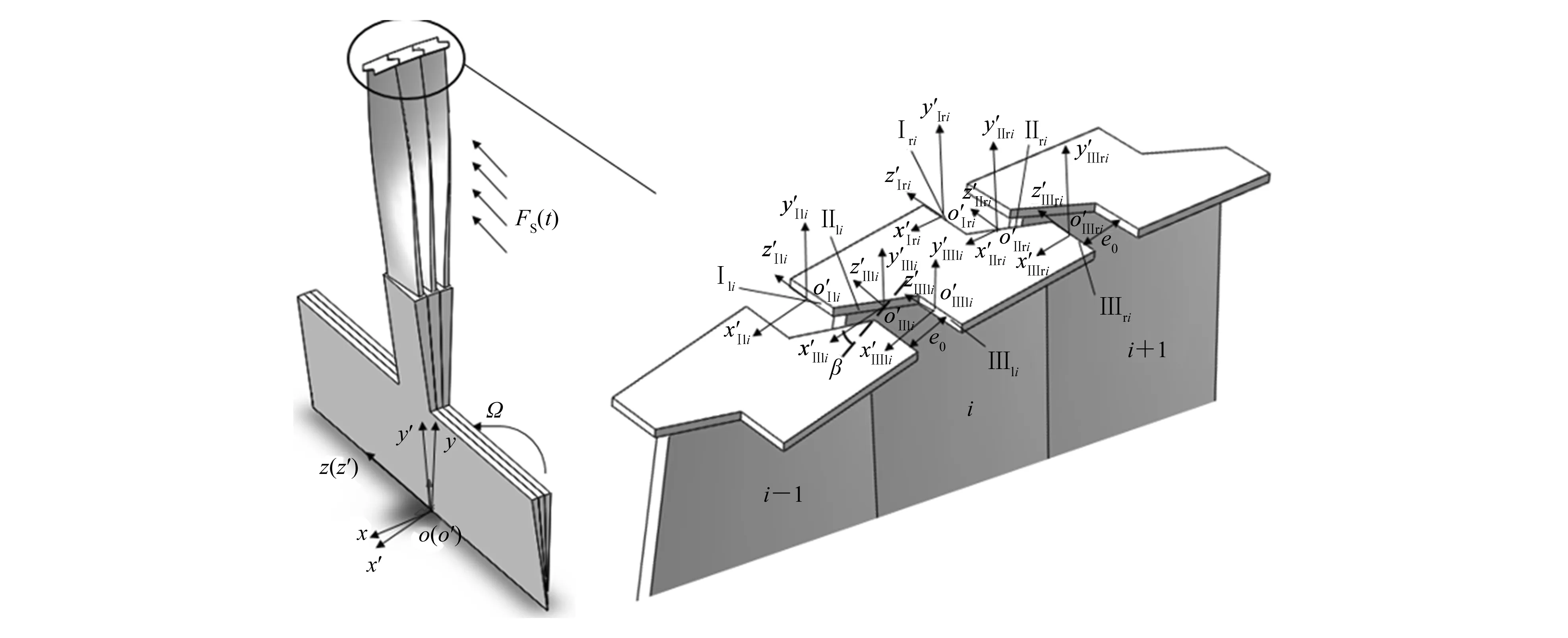
图1 末级转子的Z形围带
1.1 转速和湿蒸汽激励下围带碰撞-摩擦阻尼模型
采用快速傅里叶变换(fast Fourier transform,FFT)可将包含转速等效离心激励FΩ(t)和湿蒸汽激励FB(t)的外部激励FS(t)表示为若干个谐波激励分量的叠加[5],即:
(1)
式中:Fa(y′)为第a阶谐波激励分量的幅值;ωa和φa为激励分量的频率和相位角;t为时间;D为谐波激励最大阶数。
基于Rhee等[6]的假设,按时间顺序将围带间运动简化为如下循环运动过程:碰撞—黏滞—滑动摩擦—黏滞—分离—再碰撞。区别于平行四边形围带,Z形围带在一个运动周期的不同时间段内有不同的接触面间发生接触运动。本文用弹簧模型[2]来描述相邻围带间的法向碰撞力fim(t),用指数衰减[7]迟滞摩擦模型描述相邻围带间的切向摩擦力fif(t),建立弹簧碰撞-指数衰减迟滞摩擦模型来描述Z形围带间运动。
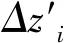

图2 fif(t)变化回线
t6至t7,Ⅱli面与Ⅱr(i-1)面间相对法向位移从0逐渐增大,增大到e0tanβ时(即t7时刻)相邻围带开始接触,t7时刻围带接触面间无作用力;t7至t11,这对接触面切向经历“黏滞—相对滑动—黏滞—反向相对滑动”运动过程;从t11开始,相邻围带分离,fif(t)和fim(t)突降为0。随着叶片振动,相邻围带再开始新一轮循环运动过程。上述一个循环周期“t0—t6—t12”中,fif(t)和fim(t)可表示为:
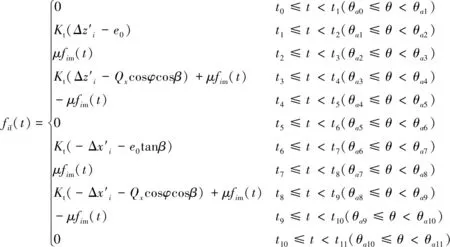
(2)
(3)

(4)
式中:Kt和Kn分别为围带接触面的切向接触刚度和法向接触刚度;μ为指数衰减模型中的摩擦系数[7];vr为围带间相对滑动速度;μd为动摩擦系数;μs为静摩擦系数;dc为衰减系数;φ为转子转角,φ=Ωt;Qx和Qz为o-xyz下Z形叶片围带振动位移分量;t0~t11为各个状态的转换时刻点;θai为各个时刻点对应的振动相位角。
θa0=-π/2
θa1=arccos[e0/R(t1)]
θa2=arccos{[e0/R(t1)]+μ[KnR(t4)tanβ+KnQzsinβ-Kne0]/[KtR(t2)]}
θa3=0
θa4=arccos{1-2μ[KnR(t4)tanβ+
KnQzsinβ-Kne0]/[(Kt+2μKntanβ)R(t4)]}
θa5=-θ1
θa6=π/2
θa7=arccos[e0tanβ/R(t7)]
θa8=arccos{[e0tanβ/R(t7)]+μ[KnR(t10)-KnQzcosβ-Kne0tanβ]/[KtR(t8)]}
`θa9=π
θa10=arccos{1-2μ[KnR(t10)-KnQzcosβ-Kne0tanβ]/[(Kt+2μKn)R(t10)]}
θa11=2π-θ7
θa12=3π/2
式中:R(t)=Qxcosφcosβ。

(5)
(6)
(7)
(8)
式中:
综上可知,已知Z形围带接触面间切向力和法向力的各段起止时间及Z形围带的瞬时振动响应位移即可求得Z形围带碰撞-摩擦阻尼,但只通过式(1)~(8)无法对其求解,因此本文提出一种围带碰撞-摩擦阻尼的计算方法。
1.2 围带碰撞-摩擦阻尼计算公式及方法
转子系统的质量矩阵Ms、刚度矩阵Ks、转子系统围带碰撞-摩擦等效刚度矩阵Mfm、等效阻尼矩阵Cfm和转子系统位移矢量Q(t+τ)关系为:
(9)
(10)
(11)
(12)

(13)
其中:

(14)
式中:g为系统叶片数;Msi,Ksi,Kifm和Cifm为第i个带围带叶片及其对应角度下轮毂及轴的质量矩阵、静刚度矩阵、围带碰撞-摩擦等效刚度矩阵和围带碰撞-摩擦等效阻尼矩阵;τ为迟滞时间;T′为o′-x′y′z′与o-xyz的变换矩阵。
考虑围带碰撞-摩擦阻尼的转子系统振动微分方程为:
(15)

转子系统临界阻尼ccri的表达式为:
ccri=2msωnfm
(16)
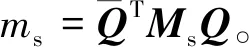
(17)

(18)
式中:Ast/Ast+T为系统振幅比,Ast和Ast+T分别为t时刻和(t+T)时刻系统在不同工况激励下振动位移响应幅值;T为系统振动周期。则转速和湿蒸汽激励下围带碰撞-摩擦阻尼cfm为[4]:
(19)
由式(18)和式(19)可知,为了求解围带碰撞-摩擦阻尼,需要利用模态分析确定系统模态质量和固有频率;需要利用瞬态响应分析得到系统在不同工况激励下振动位移响应幅值。据此,本文建立转速和湿蒸汽激励下围带碰撞-摩擦阻尼计算方法,具体步骤如下:
1)用三维建模软件建立相邻Z形围带间法向初始间隙为e0、接触角为β的转子系统三维几何模型,然后导入ANSYS中进行离散,得到有限元模型;
2)用ANSYS模态分析模块对有限元模型施加转速,得到系统模态质量ms和固有频率ωnfm;
3)用ANSYS建立并离散包含静叶和动叶的流体计算域,导入CFX中,进行流场仿真得到压力分布载荷,用FFT变换得到湿蒸汽激励FB(t);
4)用ANSYS Explicit Dynamics 模块对有限元模型做前处理,设置接触条件中的摩擦系数μd及μs、衰减系数dc和接触刚度Kt及Kn,施加Ω和FB(t),调用ANSYS LS-DYNA求解器LS-PrePost做后处理,得到系统最大振动位移响应曲线,代入式(18)和式(19)计算可得Cfm。
2 实例计算分析
以某1 000 MW大型汽轮机低压末级转子系统为例,Z形围带参数为β=30°,e0=0.5 mm,μs=0.05,Kn=0.2,叶片长度L=1 400 mm,采用轴向对称性、相对柔度法和CN群论法缩减转子系统至包含3个带Z形围带的叶片及其对应角度下轮毂和轴的基本扇区,采用本文提出的围带碰撞-摩擦阻尼计算方法定量计算围带碰撞-摩擦阻尼及其对转子系统振动特性的影响,并用本文提出的围带阻尼计算方法计算得到的文献[8]中实验叶片组的振动响应振幅比与文献实验数据进行对比。
2.1 Z形围带碰撞-摩擦阻尼及其对系统振动特性影响
采用本文提出的围带阻尼计算方法中步骤1)和步骤2)对转速Ω=1 500 r/min下的转子系统进行模态分析,得到表1中系统前5阶的固有频率。
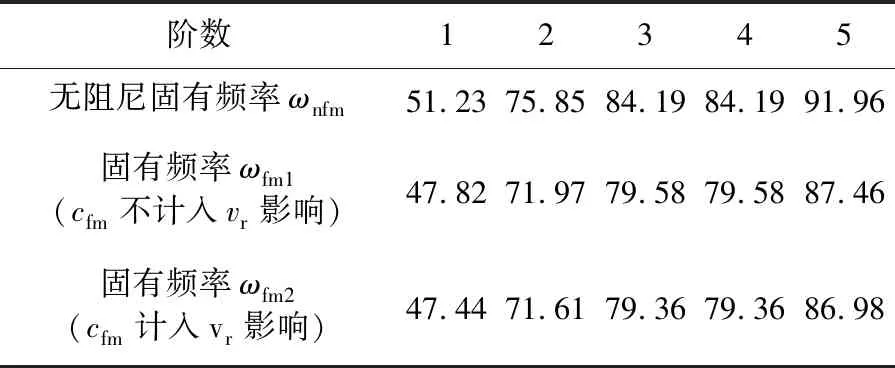
表1 转子系统的前5阶固有频率 单位:Hz
由表可知,Z形围带碰撞-摩擦阻尼使系统第一、二阶固有频率均远离转速激励倍频,影响较大,且忽略vr影响的cfm1比考虑vr影响的cfm2对系统固有频率的降低效果差但差别不大。
采用围带阻尼计算方法中步骤3) 和步骤4)对额定流量工况下的转子系统进行瞬态响应分析,得到系统振动响应位移曲线及振幅比,计算得到的cfm列于表2。

表2 转子系统的围带碰撞-摩擦阻尼
由表可知,Z形围带碰撞-摩擦阻尼降低了系统振动位移响应幅值,影响较大,考虑vr对cfm的影响和FB(t)幅值变化的围带接触模型的cfm比不考虑上述影响的cfm对系统振动响应特性影响小。
2.2 阻尼模型及计算方法的验证
本文采用围带阻尼计算方法对文献[8]中不同初始间隙e0下带Z形围带的实验叶片组建模,施加实验激励进行瞬态响应分析得到振动位移响应,所得振幅比与文献[7]实验数据中的响应振幅比的误差见表3。
由表可知,两者误差小于13%,证明本文提出的Z形围带碰撞-摩擦阻尼模型及其计算方法是可行的。分析可知,小初始间隙区间的转子系统围带碰撞-摩擦阻尼较大,围带碰撞摩擦运动减振效果也较好,且Z形围带碰撞-摩擦阻尼随着初始间隙的增加呈现出先降低再升高后降低的变化趋势。

表3 计算得到不同e0下文献[8]中带Z形围带的
3 结论
针对大型汽轮机末级转子系统Z形围带阻尼模型未能考虑围带间相对滑动速度影响、现有计算方法无法定量得到考虑围带间相对滑动速度影响的Z形围带碰撞-摩擦阻尼等问题,本文建立了在转速和湿蒸汽激励下考虑围带间相对滑动速度影响的Z形围带弹簧碰撞-指数衰减迟滞摩擦模型,并提出一种Z形围带碰撞-摩擦阻尼计算方法,由计算结果可得如下结论:
1)Z形围带碰撞-摩擦阻尼降低了转子系统的固有频率和振动位移响应幅值,对系统振动特性的影响不可忽略;
2)Z形围带碰撞-摩擦阻尼中的围带间相对滑动速度因素对系统固有频率的降低效果影响不大,考虑围带间相对滑动速度和湿蒸汽激励幅值沿叶高变化的Z形围带碰撞-摩擦阻尼比不考虑上述影响的围带阻尼对系统振动响应特性影响小;
3)Z形围带碰撞-摩擦阻尼随着初始间隙的增加呈现出先降低再升高后降低的变化趋势,将采用此计算方法得到的文献中带Z形围带叶片组的振动响应幅值比与文献实验数据进行对比,误差小于13%,验证了本文提出的阻尼模型及计算方法,为工程通过调节影响参数抑制转子振动提供了理论依据和实施方法。

