中和滴定曲线解读
>>>董鸿志
中和滴定曲线是对中和滴定过程定量化、图形化的表示,曲线上的点几乎覆盖了中学常见电解质溶液的各种组成,隐含信息丰富,是高考考查溶液中离子浓度关系和电离常数、水解常数的常见题型。
一、中学常见中和滴定曲线形式
中和滴定曲线形式很多,下面列举几种常见曲线图,其中图1—图3是基本形式,描述溶液pH值在滴定过程中的变化,当反应完成时会出现pH值突跃。一般说来,碱滴定酸时,如果是多元弱酸,会出现多个pH值突跃(如图3),且相同浓度下,酸越强,pH值突跃范围也就越大(如图2)。图4—图6是各种变式中比较重要的,描述滴定过程中两个相关物理量之间的关系。

图1

图2
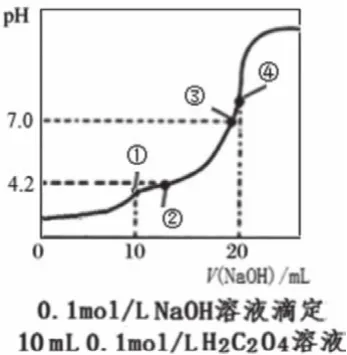
图3

图4
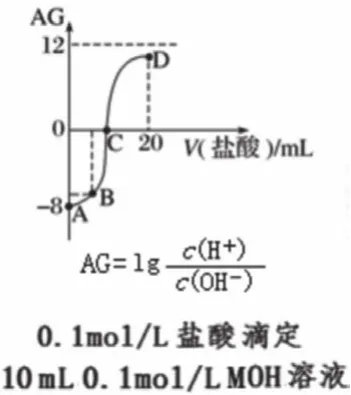
图5
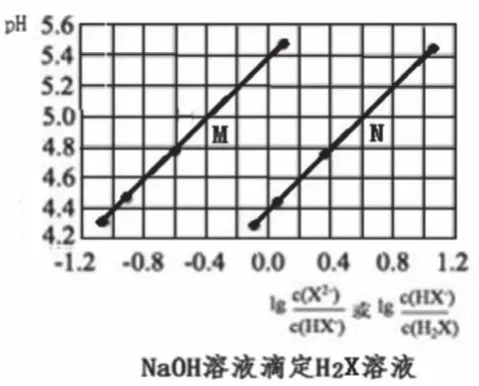
图6
二、中和滴定曲线的关键点分析
1. 起点
此时溶液中溶质是酸(如CH3COOH)或碱(如NH3·H2O)。
根据起点的pH可以判断酸或碱的强弱。如图2中,三种酸HA、HB、HD浓度均为0.1mol/L,但是pH均大于1,说明三种酸均为弱酸,且pH越小,酸性越强,酸性HA>HB>HD;若是碱,则pH越大,碱性越强。
根据起点溶液pH值,可以计算酸或碱的电离常数。如计算图2中HB的电离常数Ka。
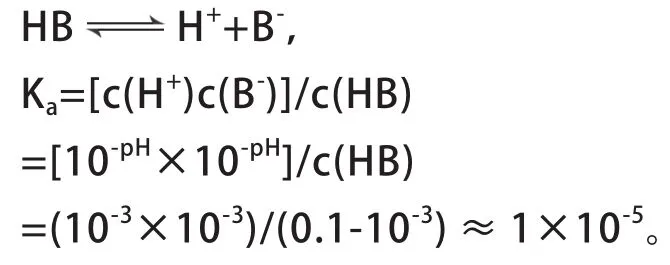
2. 中和点
中和点是恰好反应的点,根据化学计量数确定对应的酸碱用量,在图中找出相应的点,如图1中的d点、图3中的④点等。此外,利用滴定反应的特征,也可以根据溶液温度最高点、中和百分数为100%等确定中和点。如果是二元弱酸的滴定,会有两个中和点,分别对应酸式盐和正盐(如图3中的①点和④点)。需要说明的是,中和点不能通过直接观察得知,常借助于指示剂的颜色变化来确定反应完成从而终止滴定,指示剂的变色点即为滴定终点,中和点和滴定终点之间有微小误差。中学阶段用滴定曲线进行判断、计算时,通常忽略误差。
中和点溶质一般是盐(如CH3COONa、NH4Cl、NaHA、Na2A等)。
根据中和点盐溶液的pH可判定形成盐的酸、碱的相对强弱,以及溶液中离子浓度的大小关系。如图2,HA、HB、HD的中和点的pH均大于7,且依次增大,则HA、HB、HD均为弱酸且酸性依次减弱。二元弱酸的滴定中,根据恰好生成酸式盐时溶液的pH判断酸式酸根离子的电离和水解程度的相对大小,如图3的①点pH<7,判断出NaHC2O4显酸性,因此HC2O4-的电离程度大于水解程度,从而判断溶液中离子浓度的大小。
根据中和点盐溶液的pH,可计算水解常数、电离常数。如图1的d点,若pH=m,则c(H+)=10-m,c(OH-)=10m-14,根据CH3COONa水解反应c(OH-)]/c(CH3COO-)=(10m-14×10m-14)/(0.05-10m-14),Ka=Kw/Kh,代入即可求得。
3. 中性点
中性点是指c(H+)=c(OH-),常温下pH=7的点,如图3的③点、图5的C点。当反应生成可水解的盐时,中性点常见的溶液组成是盐与少量弱电解质混合。例如,用同浓度的NaOH溶液滴定CH3COOH溶液,达到中性点时,溶液中溶质为CH3COONa与少量CH3COOH;如果用同浓度的盐酸滴定NH3·H2O溶液,达到中性点时,溶液中溶质为NH4Cl与少量NH3·H2O。
中性点常用于代入电荷守恒,判断盐中的阴阳离子浓度关系。如图3的③点,根据c(H+)+c(Na+)=c(OH-)+2c(C2O42-)+c(HCO4-),得出c(Na+)=2c(C2O42-)+c(HCO4-)。
4. 等料点
等料点是指滴定反应完成一半的点,如图1中的b点、图2中的P点,此时溶液中的溶质是酸(碱)与盐等物质的量浓度的混合点。“料”表示“物料”,此点遵循物料守恒,2c(Na+)=c(酸分子)+c(酸根离子)。
根据此点的pH值,可判断弱酸(弱碱)的电离与盐的水解能力的相对大小,再根据Ka×Kh=Kw,粗略判定电离常数或水解常数的大小。
如图2中的P点,当中和百分数为50%时,一半的HB被中和生成NaB,还剩余一半的HB,则溶液相当于等物质的量浓度的NaB与HB的混合液。观察滴定曲线,此时的pH<7,则B-的水解能力小于HB的电离能力,常温下 Ka(HB)>10-7,此时,c(B-)>c(HB),若要c(B-)=c(HB),NaOH溶液的用量比此点用量略少。反之,假如此时的pH>7,则B-的水解能力大于HB的电离能力,常温下Ka(HB)<10-7,此时c(B-)<c(HB),若要c(B-)=c(HB),NaOH溶液用量比此点用量略多一点。
5. c(酸根离子)=c(酸分子)的点
像图1—图3这样的滴定曲线基本形式不易表示出此点,一般此点出现于滴定曲线的各种变式中。如图4的M、N点,图6中曲线M、N上横坐标为0的点。
图6中,横纵标为0时,M曲线的pH=5.4,N曲线的pH=4.4,分别计算出M曲线对应的Ka=10-5.4,N曲线对应的Ka=10-4.4。根据二元弱酸Ka1=[c(HX-)c(H+)/c(H2X)] >Ka2=[c(X2-)c(H+)/c(HX-)],则曲线N表示pH与lg[c(HX-)/c(H2X)]的变化关系,曲线M表示pH与lg[c(X2-)/c(HX-)]的变化关系。
三、利用滴定曲线解决电解质溶液问题的思路和方法
中和滴定曲线是解决电解质溶液相关问题的图形依据,要用好滴定曲线上的关键点,从关键点获取有关电解质溶液的相关信息,进行正确的定性和定量判断,主要有三步:
1. 准确识图
观察曲线形式、走向和横纵坐标,明确曲线的化学意义。
2. 选取关键点
观察曲线中给定数据的点,判断它是滴定曲线上的哪个关键点,明确对应的溶液溶质组成和性质特点。
3. 定性、定量判断
对选取的关键点,结合电荷守恒、物料守恒、质子守恒、Ka及Kh的计算式、与对数相关的数学计算等,解答相应问题。
例1.(2020年全国卷I,13题)以酚酞为指示剂,用0.1000 mol·L-1的NaOH溶液滴定20.00 mL未知浓度的二元酸H2A溶液。溶液中,pH、分布系数δ随滴加NaOH溶液体积VNaOH的变化关系如下图所示。
[比如A2-的分布系数:
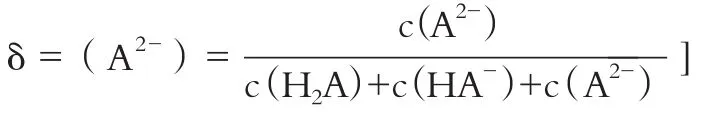

下列叙述正确的是
A.曲线①代表δ(H2A),曲线②代表δ(HA-)
B.H2A溶液的浓度为0.2000 mol·L-1
C.HA-的电离常数Ka=1.0×10-2
D.滴定终点时,溶液中 c(Na+)< 2c(A2-)+c(HA-)
【答案】C
本题为双纵坐标的二合一图像,出现新名词“分布系数”,且H2A不同于一般的二元弱酸,是罕见的第一步全电离、第二步部分电离,创新性非常强。但是认真分析发现其图像就是图1与图4的叠加,其解决过程依然源自对中和滴定曲线的深刻认知,分析过程如下:
步骤一,准确识图。
观察图像,这是将NaOH溶液滴定H2A溶液的滴定曲线及H2A溶液分布系数的变化合二为一的图像,是双纵坐标,左边为分布系数,右边是pH。
步骤二,选取关键点。
图中起点(二元酸)、两条分布系数曲线的交点(两微粒浓度相等的点)和滴定终点(二元酸对应的盐)数据清晰,可用于计算。
步骤三,定性、定量判断。
四个选项围绕H2A展开,因此,首要问题是判断H2A是什么样的二元酸。
从分布系数看,H2A若是二元强酸,则起点溶液中只存在A2-,现在起点分布系数显示有两种微粒,因此H2A不是二元强酸。从弱酸角度看,如果H2A溶液中存在则起点粒子有三种H2A、HA-、A2-,而起点只给出两种粒子的分布系数,且随滴定的进行,到达滴定终点时一种粒子的分布系数为1,另一种粒子的分布系数为0,表明只有这两种粒子,于是我们可以推测H2A第一步全电离,第二步部分电离,两种粒子是 HA-、A2-。
利用滴定终点,H2A+2NaOH=Na2A+2H2O,V(NaOH)=40mL,计算:

再看起点,pH≈1,且略小,证实上述关于H2A的推测是正确的。
A.滴定时,HA-与OH-反应生成A2-,δ(HA-)随着NaOH的滴入逐渐减小,在滴定终点几乎为0,为曲线①;δ(A2-)逐渐增大,在滴定终点接近1,为曲线②。A错误。
B.根据分析,c(H2A)=0.1000mol/L,B错误;
D.用酚酞作指示剂,酚酞变色pH范围为8.2~10,终点时溶液呈碱性,c(OH-)>c(H+),溶液中的电荷守恒为c(Na+)+c(H+)=2c(A2-)+c(HA-)+c(OH-),则c(Na+)>2c(A2-)+c(HA-),D错误。
综上所述,运用中和滴定曲线解决溶液中的相关问题,是按照识图→选点→判断的思路,紧紧抓住中和滴定曲线的基本知识,根据各种情况灵活判断。这种思路和方法,不仅适用于中和滴定,还适用于沉淀滴定、氧化还原滴定、络合滴定等。

