一种基于单光子的多方量子价格谈判协议

薛鼎蔚， 张 龙，2

（1.黑龙江大学 数学科学学院，哈尔滨150080；2.黑龙江大学 黑龙江省复杂系统理论与计算重点实验室，哈尔滨150080）

0 引 言

众所周知，电子谈判在电子商务领域有着广泛的应用［1-4］，是一种利用现代化的科技手段来实现非面对面的谈判方式。谈判的目的是在两个或两个以上的参与方之间达成一个共识［5-6］，使参与谈判的各方通过对方的行为来获得某种利益［7-8］，是取得各自经济利益的一种方法和手段。

在电子谈判过程中，随着谈判效率的提升，交换数据的安全性也受到了人们的广泛关注。2005年，Chakraborty等提出了一个基于安全多方计算（Secure multi-party computation，SMC）的隐私保护电子谈判协议［1］，提出了几种基于分布式SMC算法并试图通过优化供应链的总成本来寻找买方和卖方的共同收益，同时在协议的执行过程中不向对方或中介代理泄露成本信息。2007年，AL-JALJOULI等又提出了一个用于保护移动代理在电子谈判过程中交换信息的安全协议，并表示该协议具有隐私性、不可否认性、真实性、匿名性和交换信息的强完整性［4］。但这些经典的价格谈判协议的安全性主要是基于对计算复杂度的假设，易受到量子计算机的攻击。因此，如何利用量子技术来保证谈判协议的安全性已成为一个新的研究热点。

量子价格谈判（Quantum price negotiation，QPN）是将量子技术应用于价格谈判协议的设计中，使协议的安全性基于量子的物理特性，以避免受到量子计算机的攻击。同时，量子价格谈判也是量子保密比较（Quantum private comparison，QPC）［9-13］在经济学领域中的一个典型应用。2019年，刘文杰等在量子环境下提出了一种隐私保护的价格电子谈判协议［14］。在该协议中，首先买卖双方各自制备一个初始态，并执行多次Oracle操作来得到相应的态，然后利用Qubit比较器来获得代表买卖双方价格比较结果的最终状态，最后，通过量子计数计算出符合交易条件的商品数量。与以往的经典协议相比，刘文杰等的协议不仅大大降低了通信成本，而且也保证了两个参与者的隐私。但值得注意的是，该协议只能统计出符合交易条件的商品个数，不能确定是哪种商品符合交易条件。

本文基于单光子和量子傅里叶变换，提出了一种新型多方量子价格谈判（Multi-party quantum price negotiation，MQPN）协议。与其他量子价格谈判协议相比，本协议在保证安全性的前提下，不仅能够统计出符合交易条件的商品个数，还可以明确哪个买家对哪种商品的出价符合交易条件。因此，具有更好的应用价值。

1 预备知识

在介绍具体协议流程之前，首先将对协议所需的相关基础知识进行简单的介绍。

1.1 量子傅里叶（逆）变换

对于计算基下的态 j〉，量子傅里叶变换（QFT）作用在 j〉上：

相应的傅里叶逆变换（QFT-1）：

故有

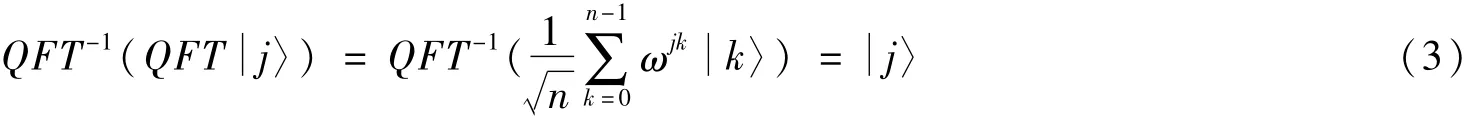
式中ω=e2πni。

1.2 相位操作

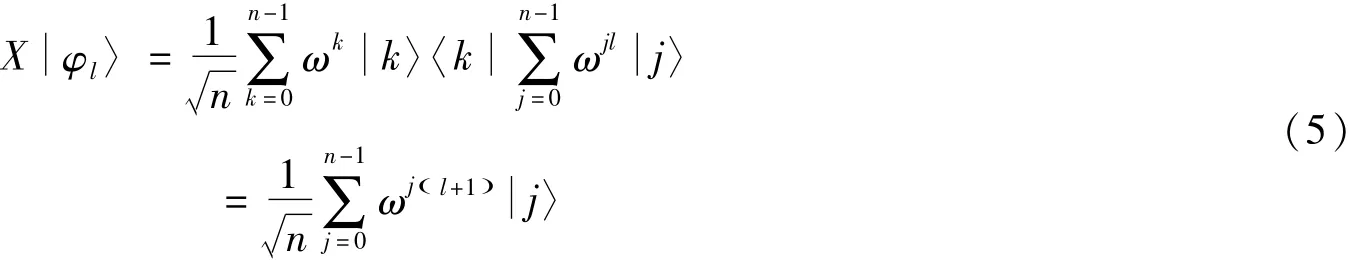
2 多方量子价格谈判协议

为了保证多方量子价格谈判协议的安全性和可用性，本协议包含三类参与方：

（1）Alicej：想要购买商品的第j个买家，其中j=1，2，…，m（m∈N*）。

（2）Bob：想要出售商品的卖家，卖家是诚实的，对于任意一种商品，在符合交易条件的情况下，他会选择出价最高的买家进行交易。

（3）TP：帮助买家和卖家达成交易的半诚实第三方。一方面，TP会严格执行协议步骤且不会与任何一个参与方合谋；另一方面，TP会根据传送到自己手中的信息来独立推断交易双方的秘密信息。

2.1 新型MQPN问题的定义

MQPN问题：对于两个谈判方Alicej和Bob（本协议考虑多个买家和一个卖家的情况），他们想对n种商品进行交易。在进行交易之前，Bob对n种商品的最低售价依次为B=（b1，b2，…，bn），Alicej的购买价格依次为（若在交易的过程中他们窃取了对方的价格信息，那么他们可以对自己的价格进行调整，以获得更大的利益）。对于买卖双方将要进行交易的第i种商品，其中i∈｛1，2，…，n｝，若存在bi，则Bob不进行交易；若存在，则符合交易条件且Bob会选择出价最高的Alicej进行交易。在整个谈判过程中，买卖双方不会泄露他们的价格信息。

另外，为了完美地解决MQPN问题，协议应该满足以下两个特点：

（1）正确性：在TP的帮助下，Bob可以准确地知道哪些买家符合交易条件，且会选择出价最高的买家进行交易。

（2）隐私性：在整个协议过程中，对于TP来说，他不能根据自己手中的信息来独立推断买卖双方中任何一方的价格隐私；对于买卖双方来说，即使买家不诚实，双方也不可能从对方处获得任何价格信息。

2.2 MQPN协议的描述

假设协议的谈判方为一个卖家Bob和多个买家Alicej，Bob对n种商品的最低售价依次为B=（b1，b2，…，bn），Alicej的购买价格依次为。存在一个自然数d，使得买卖双方的价格信息满足bi∈｛1，2，…，d-1｝和aji∈｛0，1，…，d-1｝。Bob和Alicej事先利用量子密钥分配（Quantum key distribution，QKD）协议［15-19］共享一个密钥c，其中c是一个0-1串，在这里将其编码成一个十进制数。在TP的帮助下，参与者们执行以下的步骤以完成交易。具体协议流程如下：

（2）随后，TP在傅里叶基和计算基中随机制备m+1组诱骗粒子的量子态序列s1，…，sj，…，sm，sm+1，其中每个序列都含有l个诱骗粒子，并将每个分别随机插入每组诱骗粒子中，形成新的序列s′1，…，s′j，…，s′m，s′m+1后，将序列s′1，…，s′j，…，s′m分别发送给Alicej，将序列s′m+1发送给Bob。

（3）买卖双方在确认收到s′1，…，s′j，…，s′m，s′m+1后，TP公布诱骗粒子的位置，并要求买卖双方用相应的基来测量对应位置的诱骗粒子，然后Alicej和Bob宣布测量结果。根据诱骗粒子的初始状态和买卖双方公布的测量结果，TP可以计算错误率。如果错误率不超过预先设置的阈值，那么继续谈判，否则终止协议并重新进行下一轮谈判。

（4）窃听检测结束后，买家Alicej计算αji=aji+c，再对

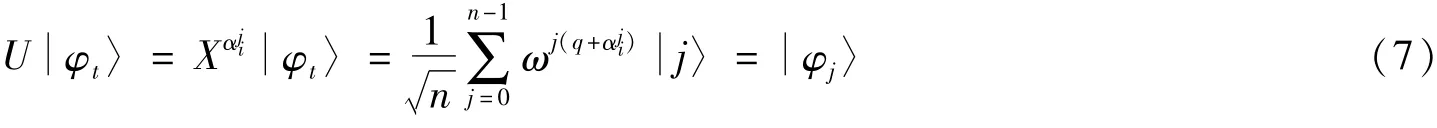
同时，Bob计算βi=bi+c，并对执行幺正操作生成，此时

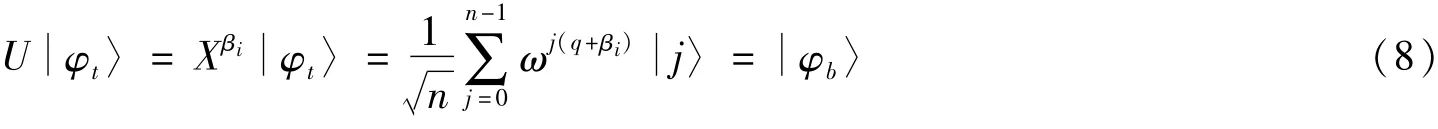
（5）Alicej和Bob各自制备一组带有l个诱骗粒子的量子态序列，分别为s″1，…，s″j，…，s″m和s″m+1，其中每个诱骗粒子都是从傅里叶基和计算基中随机选择的。随后他们将手中的态随机插入到各自制备的序列中，形成一个新的序列，分别为s‴1，…，s‴j，…，s‴m和s‴m+1，并将其发送给TP。

（6）确认TP收到s‴1，…，s‴j，…，s‴m和s‴m+1后，Alicej和Bob分别公布诱骗粒子的位置，并要求TP用相应的基来测量对应位置的诱骗粒子，然后TP宣布测量结果。根据诱骗粒子的初始状态和TP公布的测量结果，Alicej和Bob可以计算错误率。如果错误率不超过预先设置的阈值，那么继续谈判，否则终止协议并重新进行下一轮谈判。

（7）窃听检测结束后，TP分别对执行QFT-1变换，并通过计算基下的测量分别得到相位

及

（8）TP根据等式（9）和式（10），对包含Alicej和Bob价格信息的Xji和Yi进行比较。因此，对于第i种商品来说，Xji和Yi以及它们相对应的aji和bi的数学关系如下：

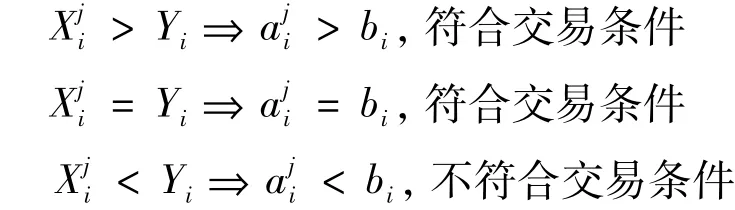
当存在两个及以上的Xji符合交易条件时，TP比较每个符合交易条件的Xji之间的大小关系，并通过已授权的经典信道向Bob公布比较结果。因此，Bob可以与满足交易条件且出价最高的卖家进行交易。MQPN协议的基本模型如图1所示。

图1 MQPN协议的基本模型Fig.1 Basic model of MQPN protocol

3 协议分析

协议的正确性，是指在所有参与方都能够诚实地执行协议的情况下，卖家可以与出价最高的买家进行交易；同时，安全性分析表明该协议可以抵抗内部和外部攻击，如参与者攻击、截获-重发攻击以及纠缠-测量攻击等，并对协议的实用性进行分析和说明。

3.1 正确性

若有多个买家Alicej（j=1，2，…，m）想与一个卖家Bob进行交易，买卖双方首先会共享一个密钥c，然后将各自的价格信息编码到TP发送给他们的量子态上。编码完成后，他们将新的量子态发送给TP，对于任意一种商品，根据QFT-1的定义，由TP对相应的量子态作QFT-1变换并用计算基进行测量，从而TP就会获得买卖双方利用密钥c加密后的价格信息，即并对买卖双方加密后的价格信息进行比较。由于TP单独制备了单光子q〉，所以TP知道q的取值，并且买卖双方预先共享的密钥c是相同的，因此，TP对Xji和Yi的比较结果即可看作是对买卖双方价格信息的比较结果，故该协议是正确的。为了更好地描述协议的正确性，以下给出一个典型的例子：

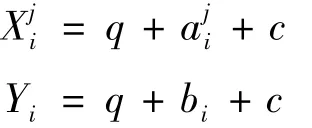
假设有5种商品，三个买家Alice1、Alice2和Alice3对这5种商品的购买价格分别为：A1=（4，3，5，4，7）、A2=（2，8，7，4，5）和A3=（8，2，6，6，3），卖家Bob对商品的售价依次为B=（3，4，5，5，7），并且他们要在TP的帮助下完成交易。根据所设计的协议，令Alice1、Alice2、Alice3与Bob之间共享的密钥c=6。省略安全检查过程，详细步骤如下：

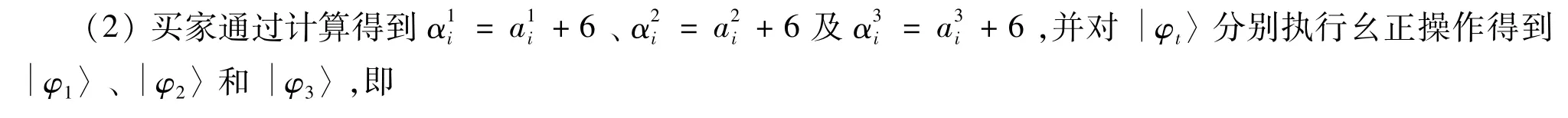
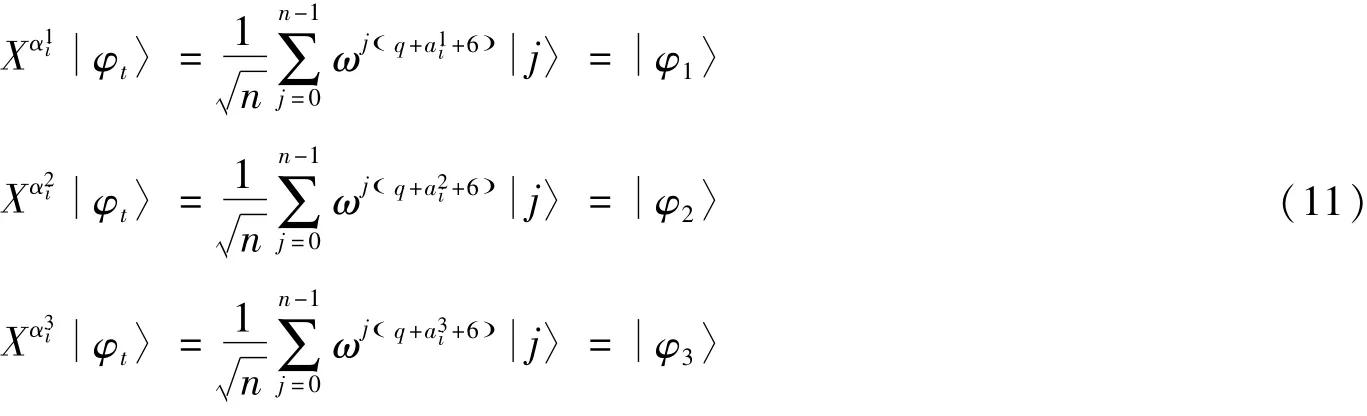
Bob计算后，得到βi=bi+6，并对执行相同的操作生成，即

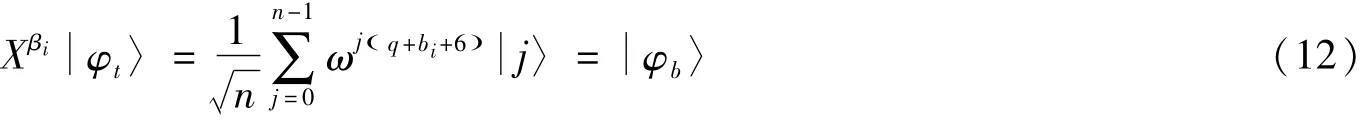
随后再对 执行QFT-1后进行测量，得到：

（4）根据式（13）和式（14），TP即可分别对买卖双方想要交易的5种商品价格进行比较。对于第一种商品来说，TP算得的结果为：

对比得出：

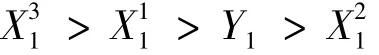
TP通过经典信道向Bob公布比较结果后，Bob与Alice3进行交易。依照此方法，买卖双方可对每种符合交易条件的商品达成交易。

3.2 参与者隐私

分别给出了Alicej和Bob价格信息的保密性，并证明他们不可能相互推断出对方的隐私信息。

3.2.1 合谋攻击

（1）多个买家合谋企图阻止另一个买家与卖家的交易

此时合谋的买家会在量子态的传输过程中截获另一个买家的量子信息以获得该买家的出价。在协议的步骤5和步骤6中，Alicej通过量子信道将每个序列s‴1，…，s‴j，…，s‴m发送给TP，并且每个s‴j中都包含l个诱骗粒子。合谋的买家知道TP分别发送给他们的量子态是相同的，一旦他们想要获得另一个买家的价格信息，他们就必须在第二次传输过程中截获该买家的量子序列s‴r（r∈｛1，2，…，m｝），并在正确的测量基下进行测量，以获得该买家的价格信息。然而，以下分析表明，他们是不可能得到准确结果的。因此，对于任意序列s‴1，…，s‴j，…，s‴m，如果合谋的买家想得到另一个买家的有用信息，他们将有两种攻击方式：

①合谋的买家直接测量被截获的粒子并且不向TP发送任何信息。在此情况下，由于TP没有收到任何粒子，或者收到序列中的粒子数小于l+1，因此，TP就会知道传输的量子序列已经被他人截获了。

②合谋的买家测量截获的粒子并且将伪造的粒子发送给TP。由于每个序列中含有l+1个粒子，其中有l个是诱骗粒子，因此，合谋者无法直接分辨出他们所测量的粒子是否是编码信息的粒子。

在这种情况下，针对任意一个序列，若他们从截获的粒子中选择一个粒子进行测量，则该粒子是诱骗粒子的概率为由于诱骗粒子是在傅立叶基和计算基下随机制备的，那么合谋者要随机选择这两个基来测量一个诱骗粒子，其选择了正确的基并且成功测量的概率为。因此，合谋者在选择了一个诱骗粒子时，能成功躲避窃听检测的概率为。若他们选择了编码信息的粒子，则能获得价格信息的概率。对于合谋者截获的该序列的粒子，他们在不被检测到的情况下获得价格信息的概率为

随着序列中粒子数的增加，合谋者不被检测的概率趋于0。因此，多个买家合谋不能获得另一个买家的价格信息。

（2）多个买家与卖家合谋

作为卖家，目的就是使自己的商品能卖出最高的价格，以实现利益最大化。因此，卖家Bob不会与多个买家合谋，并以低价将商品出售给他们。

3.2.2 独立攻击

买家和卖家的主要攻击目标就是要攻击量子信道，以获取对方的价格信息，进一步调整自己的价格以获得最大的利益。

（1）对于Alicej或者Bob来说：若Alicej（Bob）想要获取Bob（Alicej）的价格信息，他就需要知道Bob（Alicej）通过量子信道传输给TP的量子态。但由于Bob（Alicej）是将编码价格信息的量子态）随机插入到带有l个诱饵粒子的序列中进行传输的，一旦他想要截获Bob（Alicej）发送给TP的量子序列s‴m+1（s‴j），类似于买家合谋发起的内部攻击，他就会被发现。因此，Alicej（Bob）无法获得Bob（Alicej）的价格信息。

（2）对于TP来说：TP在收到Alicej（Bob）传输的量子序列后，抛弃诱骗粒子并获得 φj〉 （φb〉），然后再利用QFT-1操作得到αji（βi）。由于Alicej和Bob预先共享了一个密钥c，而TP并不知道密钥c的值。因此，TP不能获得Alicej（Bob）的任何价格信息。

由此可知，该协议有效地保障了交易方中每个人的隐私。

3.3 外部攻击

在这里，讨论外部攻击者Eve是否可以通过截获量子信道中的信息来推断或直接获得买卖双方的价格信息，即和。如果Eve是一个恶意的外部攻击者，他可以拦截量子信道中传输的量子信息。

（1）在协议的步骤2中，TP通过量子信道将每个序列s′1，…，s′j，…，s′m和s′m+1分别发送给Alicej和Bob，并且每个s′j和s′m+1中都包含l个诱骗粒子。一旦Eve想要通过获得TP发送的秘密信息来推断买卖双方价格信息，他就必须在量子信道中截获TP发送给买卖双方的量子序列，并在正确的测量基下进行测量以获得量子态。对于每一个序列s′1，…，s′j，…，s′m，s′m+1，如果Eve想得到有用的信息，他将有两种攻击方式：

①Eve直接测量被截获的粒子并且不向买卖双方发送任何信息。在此情况下，由于买卖双方没有收到任何粒子，或者各自收到序列中的粒子数小于l+1，因此，买卖双方就会知道TP传输的量子信息已经被Eve攻击了。

②Eve测量截获的粒子并且将伪造的粒子发送给买卖双方。与合谋攻击类似，Eve在选择了一个诱骗粒子时，能成功躲避窃听检测的概率为。若Eve选择了编码信息的粒子，则他能获得价格信息的概率为。对于Eve截获的m+1个序列的粒子，他在不被检测到的情况下获得价格信息的概率为，随着买卖双方规模的增加，这个概率可以忽略不计。

（2）在协议的步骤5和步骤6中，Alicej和Bob各自制备了含有l个诱骗粒子的序列s‴1，…，s‴j，…，s‴m和s‴m+1。与上述分析相同，Eve在不被检测到的情况下获得价格信息的概率同样为pe=

因此，Eve不可能直接获得买卖双方的价格信息。

3.4 实用性分析

在本协议中，m个买家可以共同对n种商品与卖家进行交易，此时，TP需要将每个Xji与Y进行比较。同时，m个买家中的部分买家也可以针对n种商品中的某一种或多种商品与卖家进行交易，这说明本协议具有很好的灵活性。同时，卖家可以与出价最高的买家进行交易，实现了买家出价高者得、卖家利益最大化的商业目标，故与现有价格谈判协议相比，本协议具有更高的实用价值。

4 结 论

本文提出了一种新的基于单光子和傅里叶变换的量子价格谈判协议，该协议利用幺正操作将参与方的秘密价格信息编码到d维单光子态的相位上，在半诚实第三方模型下，有效地保证了各参与方隐私性和安全性，且具有更好的实用性。本协议是在半诚实第三方（TP）模型下进行设计的，那么在没有TP存在的情况下，能否也可以利用单光子来设计一个安全的量子价格谈判（QPN）协议，将是下一步的研究重点。