中国省际人口迁移短期预测分析

李 建 学，蒲 英 霞,2,3*，刘 大 伟

(1.南京大学地理与海洋科学学院，江苏 南京210023；2.江苏省地理信息技术重点实验室，江苏 南京 210023；3.江苏省地理信息资源开发与利用协同创新中心，江苏 南京 210023)

0 引言

人口迁移是人口变动的三大组成之一，其发展趋势直接关系到区域人口增长、城镇化进程、经济社会发展和人类生命健康[1-5]。科学预测人口迁移流动状况，及时掌握人口活动相关信息，对于国家或地区经济和社会系统的正常运转具有重要指导意义。

人口迁移预测经过几十年的发展，已成为人口研究领域的重要方向[6-8]，相关研究大体上分为确定性预测和外推性预测两类[9-11]。确定性预测主要指场景预测，即根据过去人口迁移状况，设定未来人口迁移发生变化的几种可能(如低、中、高3种场景)，得到人口迁移场景的上下边界，回答“假如则如何(what-if)”等问题。外推性预测则指出未来某时段人口迁移在给定基本概率分布假设下发生的可能性，研究方法有时间序列分析和马尔可夫链等[12-15]，是目前我国省际人口迁移的主要预测方法。例如，邓羽等通过2000年和2010年省际人口迁移流动矩阵，利用马尔可夫链构建省际净流动初始概率矩阵，对2010-2050年省际人口流动进行了预测[14]；龙晓珺等基于全面二孩实施背景，利用第六次全国人口普查数据构建省际迁入和迁出概率矩阵，并辅助Logistics曲线拟合等方法，测算2020年省际人口总迁移量为10 921万人[15]。事实上，人口迁移是一个时空路径依赖过程[16]：一方面，过去的迁移存量可为后来迁移者提供住房或工作上的援助，减少其面对外界环境的困难和压力[17-19]；另一方面，在目的地不确定和信息不完整等情形下，人们更有可能追随周边人口迁移行为，表现出更强的羊群效应[20]。然而，现有人口迁移预测研究多关注迁移的时间维度，很少将时间和空间有机结合，在多区域人口迁移预测方面有一定的局限性[21]，无法反映人口迁移过程的本质特征，也影响迁移预测精度[22]。

特征向量时空滤波(Eigenvector Spatiotemporal Filtering，ESTF)在预测方面具有一定潜力，可从表征时空依赖关系的矩阵中提取满足一定条件的特征向量，将其作为一组控制变量加入到传统的线性或泊松模型中以提高模型拟合能力[23-25]。该模型不仅可用于预测人口迁移发展趋势[26]，还可进一步推广到商品流、贸易流或信息流等领域，为区域人口和经济社会可持续发展提供决策支持。因此，本文基于多次全国人口普查和全国1%人口抽样调查数据，采用ESTF和普通泊松模型相结合的方法，对1985-2015年间6个时期的省际人口迁移流分别构建特征向量时空滞后和时空同期滤波泊松模型，并通过评价模型的拟合程度确定合适的预测模型，最终对2015-2025年省际迁移流进行预测，探究其时空变化格局。

1 研究方法与数据来源

1.1 研究方法

1.1.1 迁移流时空依赖结构表达

(1)同一地理位置、不同时段的迁移流之间存在一定的时间自相关[21,27,28](时间依赖关系，图1a)，在时间序列数据分析中，这种依赖关系可用时间依赖矩阵WT描述[27](图1b)。当考虑一阶时间依赖关系时，相邻时段间的元素设为1，否则为0。

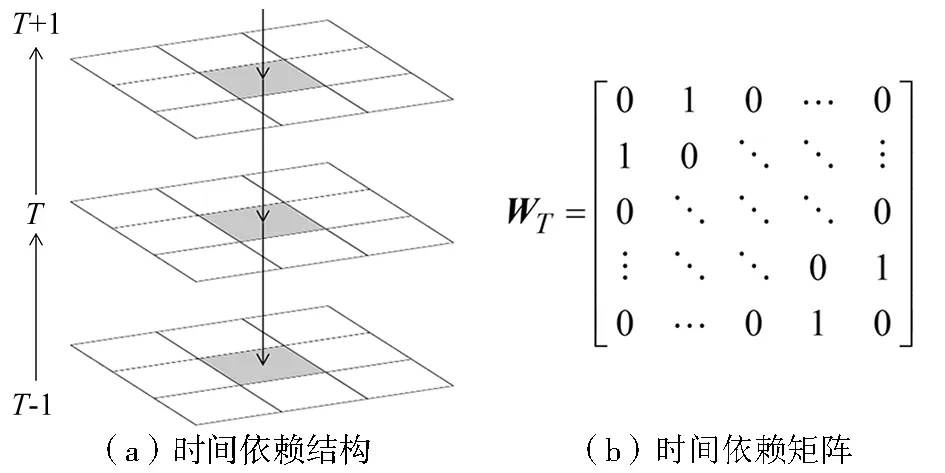
图1 时间依赖结构和时间依赖矩阵

(2)迁移流之间存在空间上的依赖关系，即网络自相关性。首先定义每条迁移流所在的迁出地与迁入地之间的依赖关系，假定地理单元数量为n，则单元之间的关系可表示为一个n×n阶空间依赖矩阵WS(图2a)，具体元素取值如下[28]：

(1)

式中：若地理单元i和j存在共同边界，则认为相邻，在矩阵中赋值为1，否则为0。

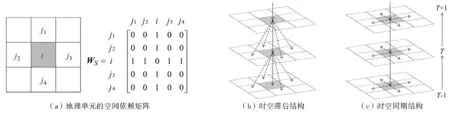
图2 地理单元的空间依赖矩阵和两种时空依赖结构

(3)在上述空间依赖矩阵的基础上进一步定义迁移流之间复杂的网络关系。目前常用的网络权重矩阵包括迁出地、迁入地和迁移流3种形式[29,30]。其中，迁出地网络权重矩阵可描述来自相邻迁出地且抵达同一迁入地的迁移流之间的关系，如在抵达广东省的迁移流中，从湖南和贵州分别出发的两条迁移流可视为邻居；迁入地网络权重矩阵可表示来自同一迁出地且抵达相邻迁入地的迁移流之间的关系，如从四川出发分别抵达广东和福建的两条迁移流可视为邻居。本文综合考虑迁出地和迁入地网络依赖两种情形，用一个N×N阶网络权重矩阵WN表示，矩阵元素取值如下：

(2)

式中：N(=n2)为迁移流条数；wS,jb=1表示迁入地j和b相邻；wS,ia=1表示迁出地i和a相邻。若迁移流为网络邻居，则矩阵元素为1，否则为0。

(4)本文综合考虑迁移流之间的时空依赖结构，分别设定时空滞后(时间滞后且相邻期空间滞后)和时空同期(时间滞后且同期空间滞后)两种结构，以探究人口迁移过程可能存在的不同路径依赖程度[25]。图2b表示时空滞后结构(Wlag)：某区域在T时段的迁移流，不仅取决于该区域T-1时段的迁移流，也取决于T-1时段周边邻居的迁移流，其矩阵表达如式(3)所示;图2c表示时空同期结构(Wsyn)：某区域在T时段的迁移流，不仅取决于该区域T-1时段的迁移流，也取决于当前T时段周边邻居的迁移流，其矩阵表达如式(4)所示。

WT⊗WN+WT⊗IN

(3)

IT⊗WN+WT⊗IN

(4)

式中：WT和IT分别为T×T阶(T为时期数)时间依赖矩阵和单位矩阵；⊗为克罗内克积；WN和IN分别为N×N阶(N为迁移流条数)网络权重矩阵和单位矩阵。

1.1.2 特征向量时空滤波方法 作为一种时空序列数据分析方法，该方法将一系列特征向量作为替代变量(或解释变量)加入到传统模型中，以提高模型对数据的拟合能力；这些特征向量来自表征时空依赖结构的网络权重矩阵，它们相互正交，互不相关。通常对时空依赖结构矩阵W进行形式变换(式(5))[28]，然后利用矩阵分解方法对式(5)提取特征向量，形成特征向量集，分别表示与矩阵W相关联的T时期N个迁移流之间的自相关结构。这些特征向量按照其特征根(时空莫兰指数，Moran′ sI)大小降序排列，通常用E=(e1,e2,…，eNT)表示，其中，e1所对应的特征根或莫兰值最大。特征向量时空滤波方法则从NT个特征向量中根据莫兰指数或赤池信息准则(AIC)等指标，遴选一组特征向量构建模型。

(5)

式中：W为时空滞后结构矩阵(Wlag)或时空同期结构矩阵(Wsyn)，为NT×NT方阵；I为N×N阶单位矩阵；l为元素全为1的N×1阶列向量。

1.1.3 特征向量时空滤波泊松模型 泊松回归模型因贴近实际计数类型的人口迁移过程而得到广泛应用[31]，考虑迁出地和迁入地要素的普通泊松模型如式(6)所示；但普通泊松模型假设迁移流之间相互独立，忽略了其中可能的网络自相关性，一定程度上降低了模型估计结果的可靠性[32]。当在模型中加入特征向量时空滤波项ETS时，可得到特征向量时空滤波泊松模型(式(7))，并显著改善模型的拟合水平。

Yij=exp(αl+Xoiβo+Xdjβd)

(6)

(7)

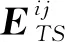
1.2 数据来源与处理

省际人口迁移流是指在较长时段上改变原来居住省份(即跨越省际边界)的人口总数,故本文将研究时段分为1985-1990年、1990-1995年、1995-2000年、2000-2005年、2005-2010年和2010-2015年，省际迁移流数据分别来源于“四普”、“五普”、“六普”以及全国1%人口抽样调查数据(1995年、2005年和2015年)，具体由统计表中“全国按现住地和5年前常住地分的人口”一项得出。在数据处理过程中，将6个时段的抽样数据分别除以各自的抽样比并保留整数，得到6个31×30阶省际迁移矩阵，共5 580条迁移流(不考虑省内迁移)。

考虑到海南省在行政上曾隶属于广东省，在空间依赖矩阵定义中将广东省作为其邻居，在此基础上分别定义时空滞后(Wlag)和时空同期网络权重矩阵(Wsyn)，并提取特征向量。此外，本文所用的解释变量包括省域GDP、总人口和距离(省会城市之间的铁路里程(km))，考虑到变量的内生性问题，选择各自时段的基期为相应数据所在年份，如1985-1990年选择1985年GDP、人口和距离数据[30,33]；考虑到GDP在不同时段之间的可比性，省域GDP数据以1985年为基期得到相应目标年份(1990年、1995年、2000年、2005年、2010年、2015年和2018年)不变价GDP(亿元)，省域GDP和人口数据来源于《中国统计年鉴》(1986年、1991年、1996年、2001年、2006年、2011年、2016年和2019年)。

2 中国省际人口迁移流预测模型优选分析

2.1 中国省际人口迁移流模型构建

以普通泊松模型为比较基准，考虑迁出地和迁入地的GDP水平、人口规模和两地之间铁路里程，考察这些变量对1985-2015年省际人口迁移的影响[34,35]。模型结构为：

yij,t=exp(α+β1O_GDPi,t+β2O_POPi,t+β3D_GDPj,t+β4D_POPj,t+β5Dij)

(8)

式中：yij,t表示t时期从迁出地i至迁入地j的人口迁移量；O_GDPi,t和O_POPi,t分别表示t时期初期迁出地i的GDP和人口；D_GDPj,t和D_POPj,t分别表示t时期初期迁入地j的GDP和人口；Dij表示迁出地i与迁入地j之间的铁路里程。

从时空同期网络权重矩阵(Wsyn)和时空滞后网络权重矩阵(Wlag)经式(5)变换后分解得到的特征向量中各选择一组大于某阈值的特征向量(ETS_syn和ETS_lag)作为候选特征向量[31]，分别代入普通泊松模型，得到特征向量时空同期滤波泊松模型(式(9)，简称“时空同期滤波模型”)和特征向量时空滞后滤波泊松模型(式(10)，简称“时空滞后滤波模型”)。

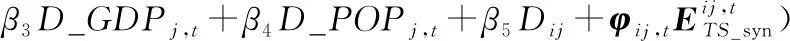
(9)

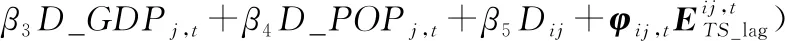
(10)

本文选用的时空网络权重矩阵在时间维度上为一阶依赖结构，在空间维度上采用基于迁入地或迁出地的网络权重矩阵(WN)。因此，6个时段的省际迁移流构成5 580×5 580阶时空网络权重矩阵，分解得到5 580个特征向量，根据阈值条件(Moran′sI/ Moran′sImax>0.25)各自选取1 074个时空同期特征向量(ETS_syn)和533个时空滞后特征向量(ETS_lag)作为候选特征向量。在R语言编程环境下，根据AIC值采用向前逐步回归方法确定时空同期滤波模型包含165个特征向量、时空滞后滤波模型包含130个特征向量。

2.2 模型系数分析

由1985-2015年中国省际人口迁移普通泊松模型、时空滞后滤波模型和时空同期滤波模型的估计结果(表1)可以看出：1)人口规模和区域GDP对迁移流的“推—拉”作用符合预期。其中，较高的人口规模和较低的经济发展水平促使本地人口外迁，而较高的经济发展水平和较低的人口规模则能够吸引大量外来人口。2)与普通泊松模型相比，时空滤波模型在一定程度上弱化了社会经济变量和距离因素对人口迁移的影响。其中，迁出地人口规模因模型设定不同而造成的弱化影响最小，表明中国省际人口迁移的主要原因之一是人口规模分布差异；而迁入地人口规模在时空同期滤波模型中明显降低，其系数绝对值仅是普通泊松模型的1/10。3)时空滤波模型的拟合效果优于普通泊松模型。通过加入经变换后的时空网络权重矩阵分解得到的特征向量，两种时空滤波模型的AIC值和RMSE明显降低，R2显著提升，表明考虑时空依赖关系的时空滞后和时空同期滤波模型对中国省际人口迁移具有更好的解释力，也进一步证实了人口迁移过程中的确存在显著的时空路径依赖。4)时空同期滤波模型的拟合结果优于时空滞后滤波模型。虽然两种模型在特征向量的数量方面接近，但时空同期滤波模型的R2更高，AIC和RMSE更低，且估计值—实际值的散点分布更为紧凑(图3),说明在中国省际人口迁移过程中，来自周边迁移流的影响大于过去迁移存量的影响，呈现同期从众特性，羊群效应较为明显。5)在时空同期滤波模型中，迁入地GDP和迁出地人口规模对迁移流影响较大。平均而言，区域GDP水平每提高1个单位，其迁入人口则会增加0.84%，迁出人口将下降0.35%。迁出地GDP和迁入地人口规模的系数显著为负，进一步验证了省际人口迁移流的普遍规律，即从人口大省迁往经济强省。

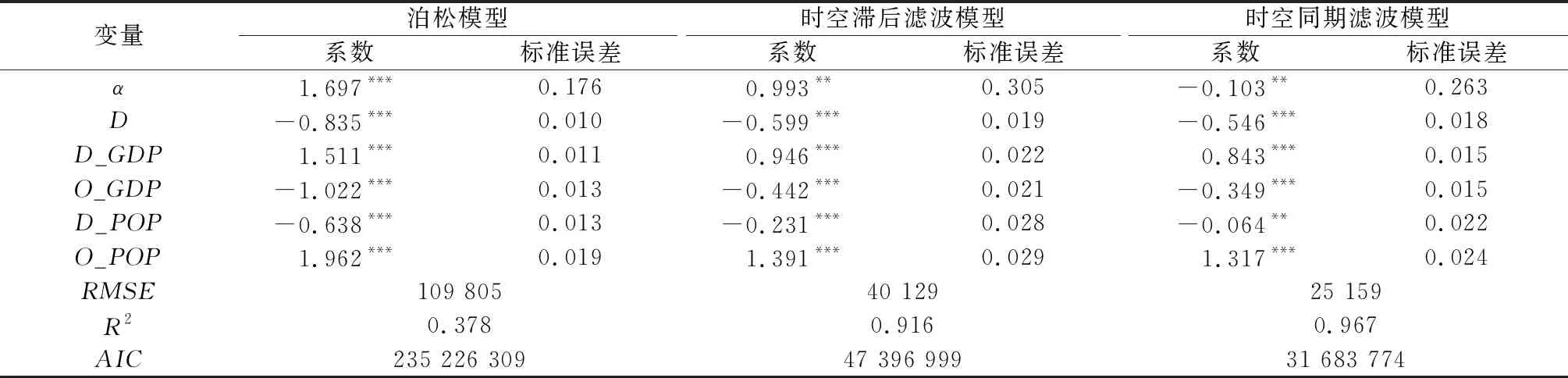
表1 普通泊松模型、时空滞后滤波模型和时空同期滤波模型人口迁移结果对比

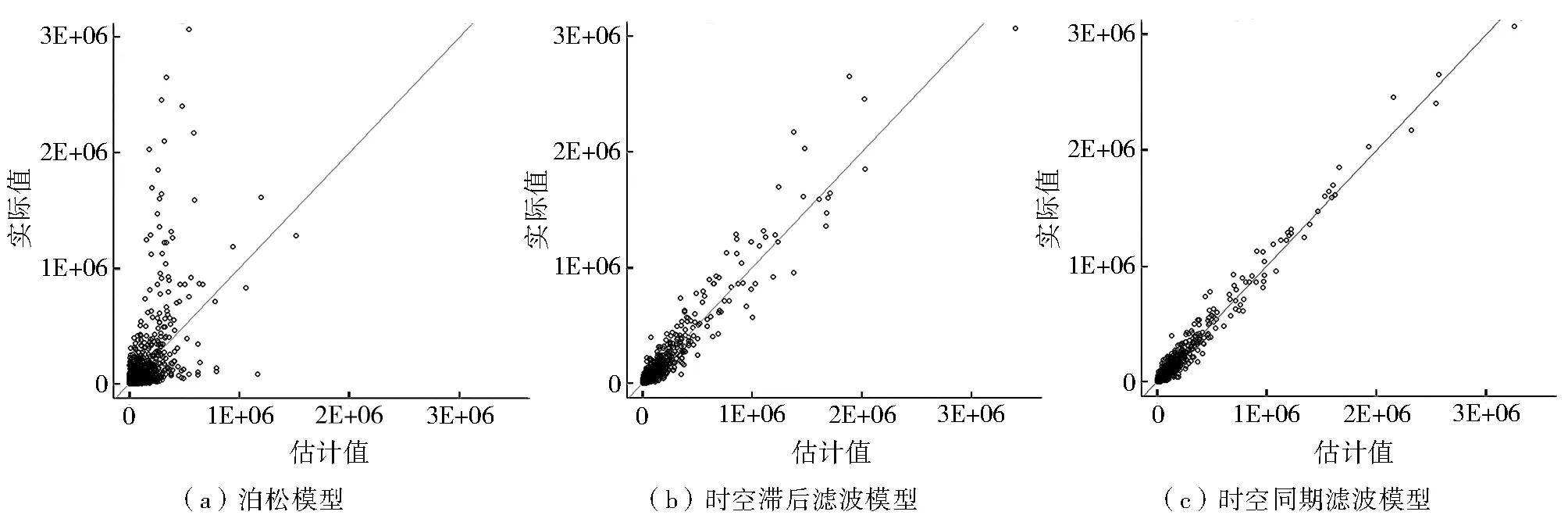
图3 3种模型的实际值-估计值散点图

2.3 模型预测精度验证

特征向量时空滤波泊松模型不仅考虑迁出地和迁入地经济社会变量和距离因素的影响，而且关注迁移流之间的时空自相关性。为进一步检验上述模型的预测性能，需要用已有数据进行验证，目前可获得的最新观测数据是2010-2015年省际人口迁移数据。下面分别利用泊松模型、时空滞后和时空同期滤波模型对2010-2015年省际人口迁移流进行估计，并与实际人口迁移流数据进行对比分析。在预测过程中，对模型做出如下假设：人口迁移流的时空分布格局在短期内不会发生较大改变，故可用前一时段的时空特征对下一时段的迁移流进行预测。模型中的人口迁移流数据来自1985-2010年5个时段全国人口普查和1%人口抽样调查数据，特征向量由基于5个时段的模型利用AIC值向前逐步回归方法筛选得到，解释变量数据来自国家统计局在相应年份发布的《中国统计年鉴》。3种模型对2010-2015年省际人口迁移流的总预测结果如表2所示。

表2 3种模型对2010-2015年迁移流预测结果比较

从表2中可以看出，3种模型的预测结果均大于实际值，这是因为模型采用了1985-2010年5个时段的实际观测数据，而该时段内的迁移总量持续上升，导致2010-2015年省际迁移流预测总量远高于实际值。其中，时空同期滤波模型的预测值最接近真实值(R2为0.901)，预测能力较强，其RMSE、MAE和AIC等也小于时空滞后滤波模型，进一步佐证了同期羊群效应在人口迁移中居主导地位。

3 2015-2025年省际人口迁移流预测分析

由于时空同期滤波模型的拟合优度和预测精度均高于普通泊松模型和时空滞后滤波模型，故本文选择时空同期滤波模型对2015-2025年省际人口迁移流进行预测。首先利用1985-2015年6个时段的省际迁移流数据以及相应时段的社会经济数据构建时空同期滤波模型，随后分别基于初期2015年和2018年社会经济数据(2020年相应数据尚不能获得)预测2015-2020年和2020-2025年省际人口迁移流量，分别得到相应时段930(31×30)条省际人口迁移流的预测均值与90%置信区间。为便于分析，将2015-2020年和2020-2025年预测结果分别按照各省域的迁入和迁出进行汇总(表3、表4)。

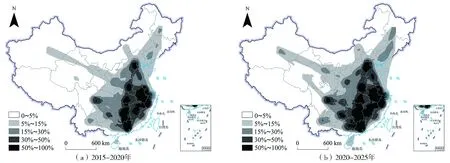
为探究迁移流的空间结构变化，对2015-2020年和2020-2025年省际人口迁移预测值进行线密度对比分析(图4)，可得如下结果：1)从整体看，两个时段的省际人口迁移预测量呈持续上升趋势。2015-2020年省际人口迁移总量预测均值达到6 776万人，90%置信区间为5 633～7 113万人，估计标准误差为380万人。该时段广东省的人口迁入总量约为1 113～1 328万人，仍为最多，浙江、江苏、北京和上海的迁入人口均值分别是700万人、626万人、448万人和440万人，比2010-2015年有显著提升；人口迁出最多的省份为河南省，其迁出人口总量均值达583万人，湖南、安徽和四川等依旧保持较高的省际迁出人口。2020-2025年人口迁移总量也将显著增长，呈现出普遍性与持续性态势，迁移预测均值将达到7 661万人，90%水平置信区间为6 825～8 606万人，广东、浙江、江苏仍然是迁入人口最多的省份。相比改革开放初期的“盲流”，未来的迁移流具有明显的方向性与目的性。2)从空间分布看，省际迁移热度呈现多区域性特点，各地区迁移热度有显著差异。2015-2020年东北地区的人口迁移热度平稳上升，但分布格局变化不大；京津地区的迁移热度逐渐向南扩散，与河南、湖北、湖南及广东等省份相互贯通，在空间上形成一条南北走向的“通道”；长三角地区的迁移热度显著上升，空间规模也逐渐扩大，表明其与周边省份的人口迁移活动越来越频繁。2020-2025年，这种“通道”的空间规模进一步扩大，但仍主要集中于东南部地区；广东省与周边省份的迁移热度显著提升，其他大多数省份的迁入流与迁出流同步增长。3)中国省际人口迁移流在空间集中上存在差异，整体上呈现不均衡特点，即迁入或迁出人口主要集中在个别区域。其中，北京和上海的迁入人口在空间上较为均衡，体现出其作为全国政治中心和经济中心的包容特点，而河北、江苏、浙江和广东等地的迁入人口主要集中在与其毗邻的几个省份。各省迁出人口在空间上也存在差异，作为人口迁出大省的湖南和广西2015-2020年有超过60%的人口迁入广东，安徽、江西、河南和四川等省的迁出人口也表现出较强的空间集聚性。

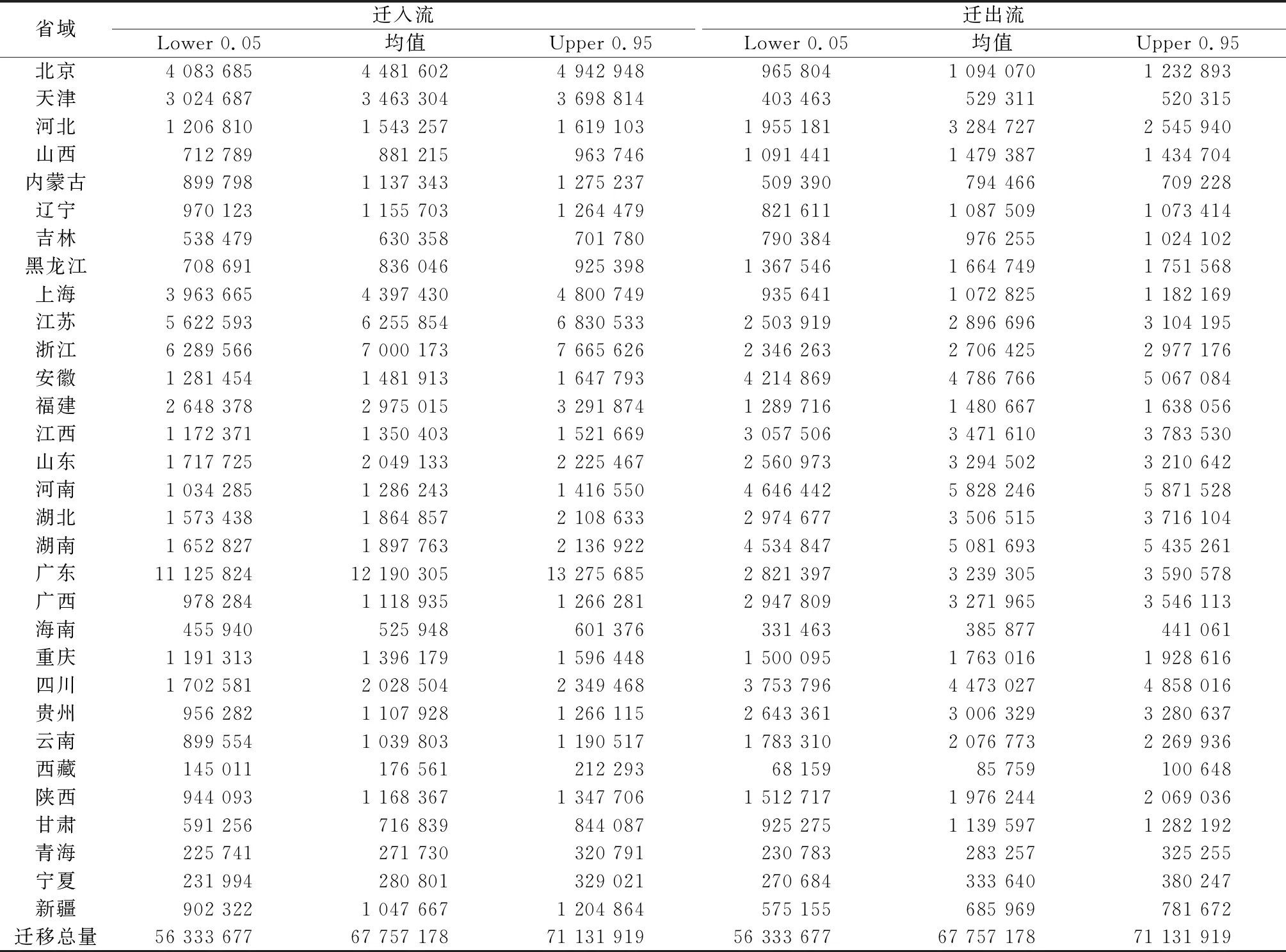
表3 2015-2020年中国省际人口迁入和迁出流预测结果

注：基于自然资源部标准地图服务网站审图号为GS(2019)1823号的标准地图制作，底图无修改。

与短期内的人口流动不同，人口迁移行为是长期且持久性的空间变化活动，与相近时段的人口迁移模式存在密切的时空关联性；虽然环境和政策等因素的影响会增加人口流动的不确定性，如受2020年新冠肺炎疫情的影响，居民出行受到限制，但从大尺度时空依赖的角度看，“长时间”的人口迁移是一个逐渐“升温”的态势。综上所述，预计中国省际人口迁移活动将更加活跃，呈现出更加集聚的空间格局。各省域的迁入和迁出空间集中度有所不同，有较强的空间异质性，珠三角、长三角及京津冀地区将依旧是迁移热点，省际迁移流在空间上将形成一条南北向的“高密度迁移带”。

表4 2020-2025年中国省际人口迁入和迁出流预测结果

4 结论与讨论

本文从人口迁移过程的时空路径依赖出发，采用特征向量时空滤波方法与普通泊松模型相结合，构建时空滞后和时空同期滤波模型，对1985-2015年6个时期共5 580条中国省际人口迁移流数据进行拟合，据此选择时空同期滤波模型对 2015-2025年省际人口迁移流量及其空间分布进行预测，结果表明：2015-2020年省际人口迁移总量均值为6 776万人，2020-2025年为7 661万人；珠三角、长三角和京津冀仍是人口迁移的主要目的地，河南、湖南、安徽及四川仍将是人口迁出大省，且在人口迁移时空惯性作用下，这些地区仍将是未来中国省际人口迁移活动的活跃区。

特征向量时空滤波方法可有效表达迁移流中可能存在的时空依赖结构关系，具有揭示人口迁移时空演变过程的潜力。与普通泊松模型相比，时空滞后和时空同期滤波模型因分别包含了当前迁移流与过去迁移存量及周边迁移流之间的内在依赖关系，均取得了较好的模型拟合效果。与时空滞后滤波模型相比，时空同期滤波模型能够更好地吻合研究时段省际迁移流数据，在区域人口迁移预测方面更具优势；特别是在当前疫情防控形势下，来自周边地区迁移流的影响明显大于过去迁移存量的影响，从侧面进一步验证了时空同期滤波模型的合理性。

人口迁移流的时空建模对其他类似空间相互作用流(商品流、贸易流、信息流等)具有重要参考意义。2020年4月，中共中央、国务院发布了《关于构建更加完善的要素市场化配置体制机制的意见》，对包括劳动力在内的其他土地、资本、技术和数据等要素如何深化市场化配置改革，促进要素自主有序高效流动提出了指导意见。人口迁移流作为劳动力要素流动的主要形式，从时空路径依赖的角度对其迁移流动机制进行探讨，并在此基础上预测未来发展状况，对其他要素流动机制的探讨提供了一定的借鉴。

本文基于不同时段、不同区域迁移流间复杂的时空依赖关系，通过特征向量时空同期和时空滞后滤波模型，定量预测时空大尺度迁移流的分布情况，为人口迁移流预测提供了新的研究视角，对人口迁移模型构建有一定贡献。但目前研究仍存在以下不足：1)人口迁移过程存在较多模式，本文仅考虑了一阶时空同期和时空滞后两种结构，模型较为简单，导致预测结果具有一定的局限性；2)人口迁移是一个多因素共同作用的复杂系统，受政治、经济、社会及环境等多方面的影响，本文只涉及人口、经济、距离和时空变量，对复杂的人口迁移过程做了简单模拟。今后将定义更多的时空依赖结构形式，考虑选择变量过程中的不确定性，提高模型的运算效率，使人口迁移模型的预测结果更加准确。