基于层次格网索引的图幅接边处等高线高程错误识别和自动修正研究
刘 康 甯,田 永 中*,沈 敬 伟,胡 晓 辉
(1.西南大学地理科学学院,重庆 400715;2.重庆稻田科技有限公司,重庆 400700;3.武汉大学遥感信息工程学院,湖北 武汉 430079)
0 引言
地表高程数据(如DEM)应用广泛[1-3],而等高线是构建DEM等的重要数据源之一[4],早期地形图存储的等高线中蕴含着丰富的历史高程信息,可有效延长地形研究的时间序列[5],对地表高程长期规律的挖掘具有重要意义。但在数字化过程中,地形图接边处易产生人为粗差[6],且两图间等高线处于分离状态,参照数据不全,易产生误判。现有软件及算法对上述错误的识别修正功能仍不完善[7]。
地形图接边处等高线质量检查的常用方法包括手工检查、地理相关法及程序自动检查等,其中手工检查人工成本高且精度无保障,地理相关法的精度过分依赖参考数据的准确性[8]。在程序自动检查方面:赵江洪[9]将数字地形图的图幅管理方式转化为格网概念,曹健等[10]和黃会平等[11]在此基础上利用格网及格网缓冲区数据优化接边算法的效率,从而提高了端点匹配的效率;He等[12]通过改进传统双向扫描方法,提出了针对等高线的高程矛盾定向扫描检查方法,但在数据量较大时算法处理效率较低;刘雄等[13]利用ArcPy进行等高线自动接边和属性一致性判断,用端点代表等高线完成属性检查,但该方法仅处理了与边界线相交的等高线,对变形等高线的适用性较低。
综上发现,当前等高线质量改善研究多关注空间位置问题[14,15],尽管涉及等高线一致性检查,但详细探讨接边算法效率改进的相对较少,且均未涉及自动修正研究。鉴于此,本文提出一种针对地形图接边处等高线高程属性错误识别及自动修正的方法,利用层次格网索引(Hierarchical Grid Index,HGI)和方向性二邻域算法(Directional Two-Neighborhood Algorithm,DTNA)提高运算效率,通过构建强空间位置关系和逻辑判断实现自动修正功能。
1 研究数据及等高线高程错误类型
重庆市酉阳县地处武陵山区腹地,是典型的喀斯特山区,地形复杂度高,选取该县1∶1万国家基本比例尺地形图作为研究数据,该数据采用Xian_1980_3_Degree_GK_CM_108E投影,共计22 142条等高线,等高距为5 m。等高线高程错误类型多样,部分数据变形明显[16,17],根据错误产生的原因,可将图幅接边处等高线高程错误分为4类:1)缺少相邻图幅内有效高程信息的参照,造成接边处等高线增减走势的判断错误;2)地形图生产人员造成的人为粗差;3)数据处理过程中产生的等高线数据变形;4)特殊地形等原因产生的伪高程错误。
2 研究方法
本文高程错误识别与修正方法的技术流程如图1所示:1)将各图幅转化为格网数据,对格网进行特殊属性构建、唯一标识化等预处理,获得辅助格网。2)读取不同图幅的等高线,并通过数据处理构建3层格网索引,实现层次格网检索。3)在方向性二邻域运算模块中:进行高程冲突识别,获取驱动因子;获取等高线空间位置标签,执行基于空间位置的快速排序;依据驱动因子,执行高程逻辑错误双向查找,进行错误判定和修正,并将修正结果汇总输出。
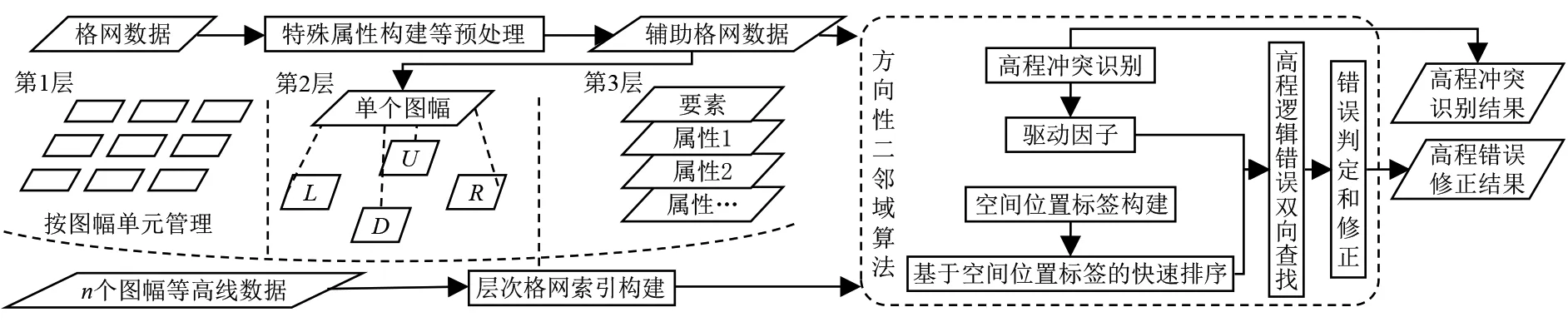
图1 本文方法技术路线
2.1 层次格网检索
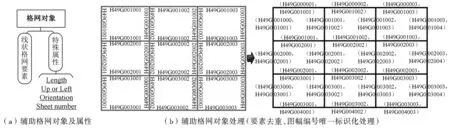
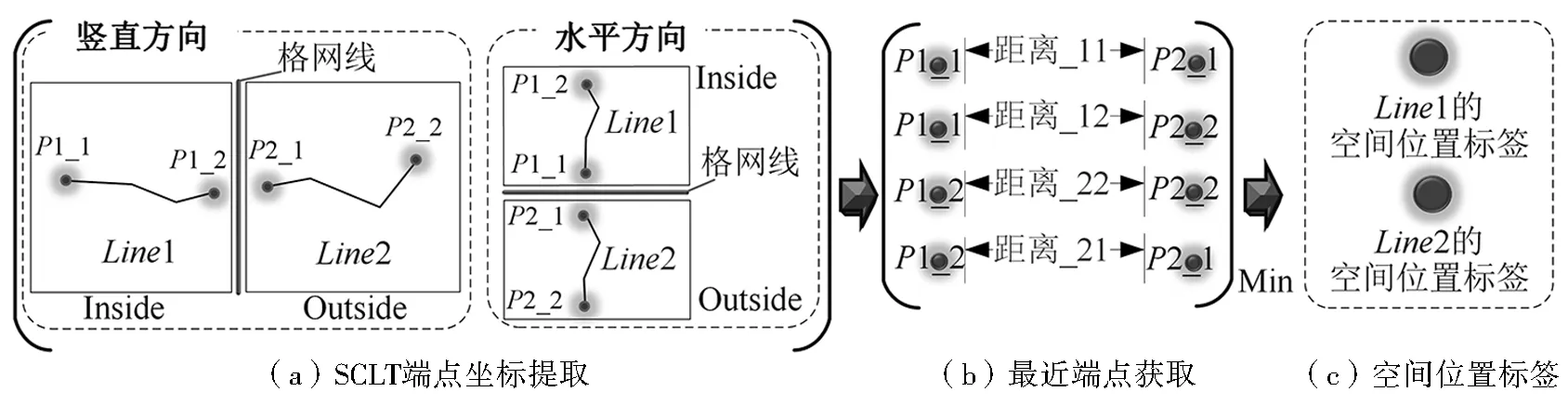
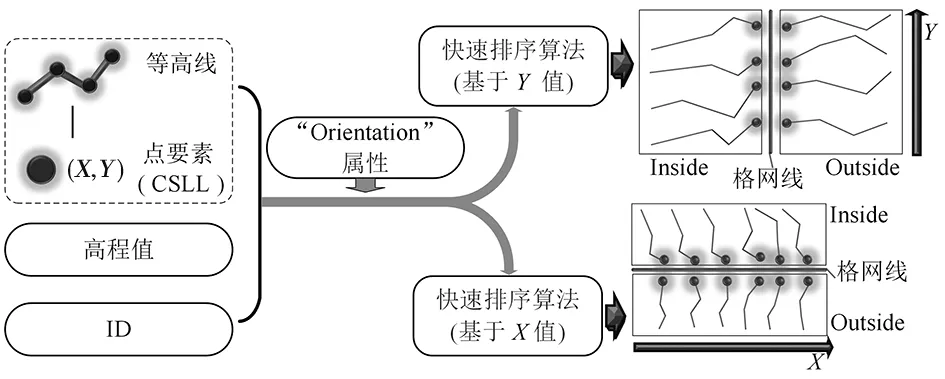
图幅是数字地形图管理的基本单位,在二维空间中等高线呈现受图幅约束的分布状态,层次格网索引能灵活高效地进行数据组织管理[18,19]。本文采用3层格网索引构建索引关系及数据结构(图2):第1层以图幅编号作为索引标签,进行单元划分;第2层对每个图幅进一步划分,借助辅助格网对象(图3)创建图幅上、下、左、右(U、D、L、R)4个方向上的空间单元,计算等高线要素与各空间单元辅助格网要素的距离,当等高线与辅助格网间关系满足式(1)时,等高线存入辅助格网对应的空间单元中;第3层将第2层索引中单个等高线的图形及属性分离存储,为满足高程错误自动修正的需求,第3层单元中添加了点单元“EndPoint”(等高线空间位置标签)。
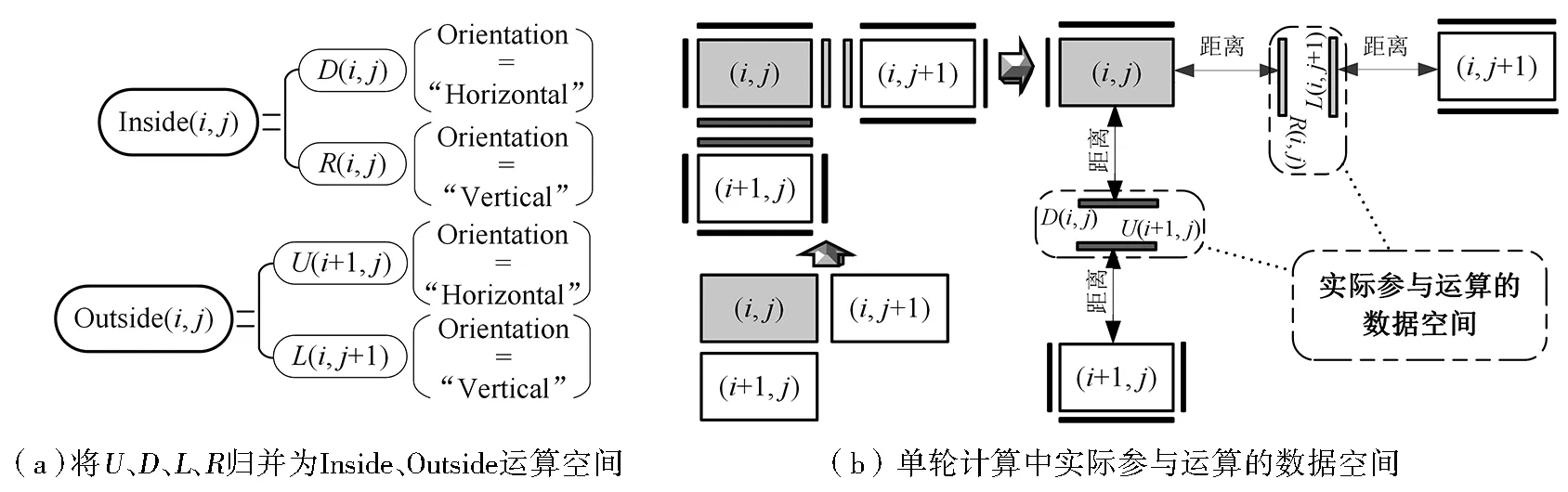
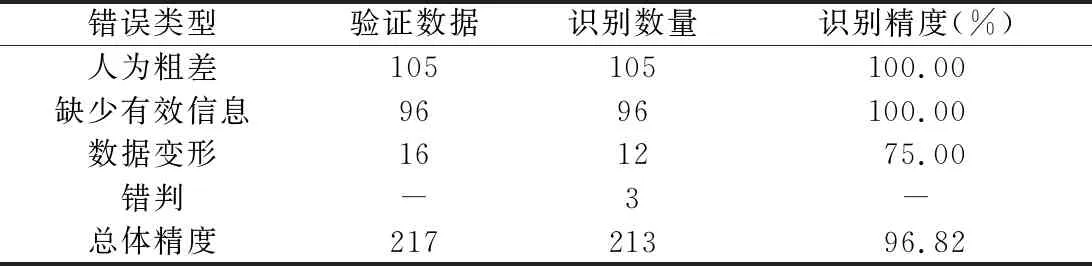
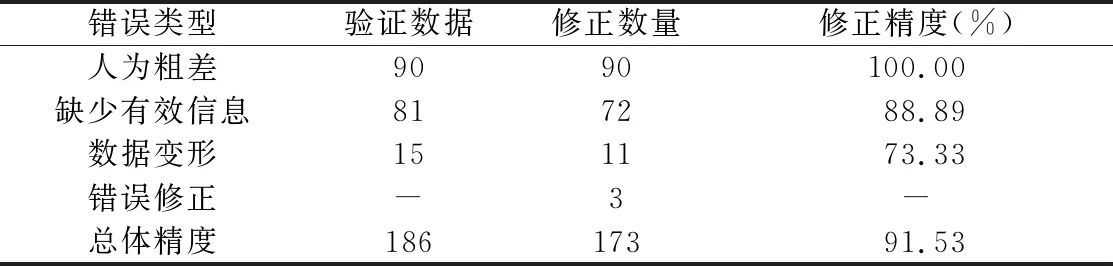
Dis(Linecontour,Linegrid) (1) 式中:Dis(Linecontour,Linegrid)为等高线要素Linecontour与格网要素Linegrid间的距离;TLine_input为判断等高线要素能否存入运算空间的阈值。 图2 层次格网索引及数据结构 图3 辅助格网对象构建及预处理 八邻域算法常被用于边界检测或对比[20],而八邻域关系中包含单元间“线共用”和“点共用”两种情况,通过对大量数据的分析可知,等高线要素落在图幅单元共用点上的可能性几乎为零,又考虑到数据运算模块的移动具有方向性,故将八邻域改进为“先右移至行末、后跳转下一行”的方向性二邻域模块。 在层次格网索引中,第2层索引对应U、D、L、R4个空间单元,本文对方向性二邻域算法进行优化,相邻图幅间接边处的数据运算实质上仅涉及(i,j)图幅的D和R单元、(i+1,j)图幅的U单元及(i,j+1)图幅的L单元(图4)。为进一步降低计算冗余,本文利用格网“Orientation”属性,将参与运算的4个空间归并为Inside和Outside两个运算空间;同时,建立两运算空间的吞吐式运算器,存入规则如图4a所示,单轮计算中仅对参与运算的两个空间进行数据填充。 图4 算法优化 2.3.1 基于空间位置标签的快速排序算法 快速排序算法产生的内循环极小,在速度上具有明显优势[21],特别是面对随机数据时,快速排序性能极好[22]。一般定义归属于同一条等高线闭合曲线的多条曲线段互为理论同一等高线(Same Contour Line in Theory,SCLT)。等高线空间位置标签(Contour Spatial Location Label,CSLL)是基于空间位置标签快速排序算法的基础,其获取方法如图5所示。仅将满足式(2)的等高线对应存进格网两侧空间中,结合格网的“Orientation”属性,通过式(3)获得关键排序参数(KSP),然后对要素及属性进行快速排序,获得空间上有序且一一对应的两等高线空间,此时,相同索引值对应的两空间中的等高线互为理论同一等高线(图6),从而构建等高线要素间的强位置关系。 (2) 式中:LineI、LineO分别为Inside、Outside空间内的等高线;TSCLT为理论同一等高线判断阈值。 (3) 式中:Point为等高线的空间位置标签;X和Y分别为横、纵坐标值。 图5 等高线空间位置标签获取 图6 基于等高线空间位置标签的快速排序算法 2.3.2 高程逻辑错误双向查找与修正 高程逻辑错误双向查找与修正的主要步骤为:1)根据判定条件(式(4)),将互为理论同一等高线且高程属性不一致的要素记为高程冲突位点,将高程冲突处Inside空间内线要素、ID及CSLL作为驱动因子进行存储汇总。2)基于已构建强空间位置关系的等高线,根据驱动因子在Inside空间中反向检索得到索引值。3)以索引值为起点在两侧空间中分别向Head和Tail方向搜索高程值逻辑错误点,进行单方向查找,直到找到逻辑错误点后停止。4)待两侧空间均完成搜索,对比两侧在Head和Tail方向上所接触到的等高线数量,数值小的判定为错误侧;若相等,分别计算两侧空间当前索引跨度n下的高程差值,差值的绝对值大于n倍等高距的一侧判定为错误。5)自动修改并记录错误等高线。 (4) 式中:LineI_E和LineO_E分别为Inside和Outside空间中等高线的高程值。 3.1.1TSCLT测试TSCLT首先需排除TLine_input的影响,当TLine_input大于或等于接边处要素与对应辅助格网间的最大距离时(本文测定结果为2.63 m),图幅中所有接边处等高线均可进入运算空间。因此,在TLine_input=3 m时,对TSCLT的设定如式(5)所示。对不同TSCLT取值下运算精度的分析(图7a)可知,TSCLT由0增至0.9 m的过程中,识别精度及修正精度均快速上升,在0.9 m处出现峰值,此时97.71%的高程冲突被正确识别,修正精度为88.89%;TSCLT>0.9 m时,识别精度呈持续下降趋势,修正精度呈波动下降趋势,在TSCLT为2.6 m和4 m时,错误配对的SCLT对自动修正的逻辑错误判断提供了额外的高程信息,修正精度出现小幅上升,但两曲线总体走势近乎一致。 (5) 式中:x=-0.1为初始值;n=1,2,…,45为迭代次数。 图7 运算精度与效率结果分析 3.1.2TLine_input通过统计分析可知,两侧图幅间SCLT要素间最邻近点的最大距离值为0.9 m,故设TSCLT=0.9 m,使TLine_input按照式(6)取值,得到精度变化情况(图7b)。由图7b可知,TLine_input为0~2.3 m时,随着存入运算空间中的数据量增加,精度不断提高,TLine_input=2.3 m时,修正精度达到最大值91.40%;TLine_input为2.4~2.7 m时,识别精度仍在上涨,TLine_input=2.7 m时,识别精度达到最大值97.71%,但修正精度出现小幅下降,最后两精度均在TLine_input=2.7 m时保持不变。 TLine_input(n)(x)=x+0.1 (6) 式中:x=0为初始值,且0≤x≤4;n=1,2,…,40为迭代次数。 作为线要素进入运算空间的判断条件,TLine_input对运算效率有直接影响,故本文讨论TSCLT=0.9 m时,不同TLine_input取值下运算耗时的变化情况(图7c)。1)当TLine_input<2.7 m时,运算效率与识别精度的变化趋势基本相似;2)当TLine_input>2.7 m时,运算精度不再发生变化,但耗时仍在不断增加,直至每次运算将所有数据存入;3)当TLine_input达到实验数据图幅尺寸的最大值6 102.78 m时,运算耗时为33 367.81 s,是TLine_input=2.7 m时(163.72 s)的203倍(向下取整)。由此可知,接边处等高线存在大量缺失或严重变形时,运算效率会降低,故本方法在处理接边处较为完整且变形较少的数据时,效率更高。 两个阈值对精度和效率均有重要影响,TSCLT主要影响SCLT的配对,合理的TSCLT能够准确构建接边处等高线的对应关系,SCLT的精准配对是实现高质量自动修正的关键;TLine_input可控制存入运算空间的要素,结合层次格网索引降低参与运算的数据量,既可保证运算精度,又可大幅提高运算效率。实验结果表明,根据数据特征获取阈值具有可行性。 自动修正前后的等高线如图8(彩图见封2)所示,其中浅蓝色、红色、深蓝色线条分别为不存在高程错误的等高线、存在高程错误的等高线和修正后的等高线。对比发现,本文方法有效识别并修正了存在高程错误的等高线数据。 (1)高程冲突识别方面(表1,TSCLT=0.9 m,TLine_input=2.3 m),总体上算法能够对“人为粗差”、“缺少有效信息”、“数据变形”3种错误类型进行有效识别,特别是针对由“人为粗差”或“缺少有效信息”造成的高程冲突几乎可以全部识别,对“数据变形”引起的高程冲突的识别精度为75.00%。除上述3种错误类型外,结果中还存在3条“伪高程错误”,致使算法产生了错判,在总体精度计算中将其计入分母。 图8 修正前后等高线对比 表1 高程冲突识别精度统计 (2)高程错误自动修正方面(表2,TSCLT=0.9 m,TLine_input=2.3 m),自动修正总体精度可达91.53%,表明算法能够对“人为粗差”、“缺少有效信息”、“数据变形”3种错误类型进行有效修正。其中,“人为粗差”的修正精度为100%,“数据变形”的修正精度为73.33%,“缺少有效信息”的修正精度为88.89%,另有3条等高线因识别过程出现错判,导致错误修改了原本正确等高线的高程值,在总体精度计算时计入分母。经进一步统计,共有9条等高线未被成功修正,其中7条位于山丘处,1条位于沟谷处,1条位于河流处。可见,未成功修正的等高线多处于地形地貌较复杂区域,地形平缓区域修正效果良好。 表2 高程错误自动修正精度统计 利用本文方法及文献[12,13]方法对实验数据进行高程冲突识别对比(表3)。文献[12]方法由于仅进行了相邻等高线间的一致性判断,对山区复杂地形的高程冲突识别效果不佳,21条等高线被错判,另有61条未能成功识别,其中51条属于区域性错误,该方法识别精度为65.55%;由于缺少有效的效率优化,其耗时67 774 s。文献[13]方法容差值与本文方法阈值设置相同,利用边界线提取和线转点的方式优化了效率,运算耗时为817.01 s;由于该方法仅对边界线上的点进行处理,错判的概率较低,但也影响了其对变形等高线的兼容性,易发生识别遗漏(该方法识别遗漏的16条等高线中有13条存在较为严重的变形)。本文方法识别结果中,3条断崖处等高线被错判,无识别遗漏,识别精度为97.73%,且层次格网索引和方向性二邻域算法的应用提高了运算效率,耗时仅为文献[13]方法的20%。 表3 不同方法对接边处高程冲突识别效果对比 本文基于层次格网索引,综合方向性二邻域算法和基于空间位置标签的快速排序算法,成功构建了接边处等高线间的强空间位置关系,快速、准确地实现了高程错误的识别和修正,为等高线数据的质量改善提供了有效方法。层次格网索引与方向性二邻域算法的结合,能够合理减少参与运算的数据量,在保证运算精度的同时,能极大地缩短运算耗时,有效提高运算效率。本文方法精度受地表复杂度的影响,在处理地貌形态较为简单的数据时精度更高;与其他方法对比,对区域性高程错误和数据变形具有更高的适用性。但本文方法对复杂地形的适用性有待提升,错误判断逻辑需进一步完善,今后可将格网索引与分布式计算相结合,进一步提高运算效率。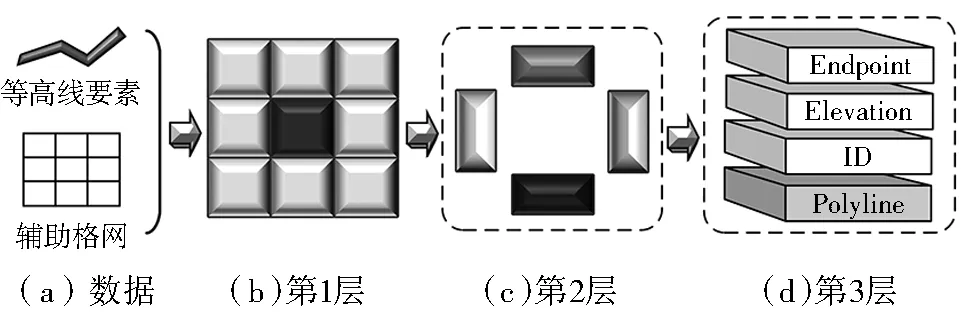
2.2 方向性二邻域算法
2.3 逻辑错误判定
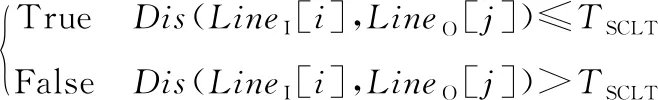

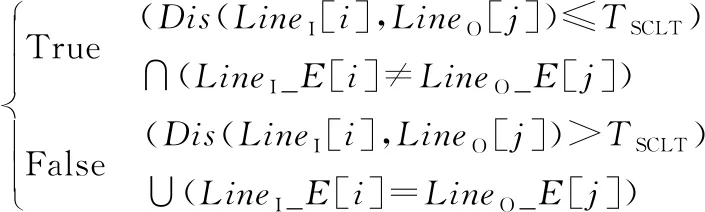
3 阈值设定对结果的影响
3.1 阈值设定对运算精度的影响

3.2 阈值设定对运算效率的影响
4 结果分析
4.1 修正效果对比
4.2 不同错误类型的识别和修正效果

4.3 不同方法识别精度及运算效率对比

5 结论

